Что это логические темы
Информатика
Основы логики
1. Основные понятия логики
Понятие
Понятие — форма мышления, в которой отражаются существенные отличительные признаки предметов.
Понятие имеет две основные логические характеристики: содержание и объем.
Содержанием понятия называется совокупность существенных признаков, отраженных в этом понятии.
Объем понятия — это множество предметов, каждому из которых принадлежат признаки, относящиеся к содержанию понятия.
Совместимые и несовместимые понятия
По объему понятия могут быть совместимыми или несовместимыми. Объемы совместимых понятий совпадают полностью или частично (т.е. существуют объекты, имеющие признаки обоих понятий). Объемы несовместимых понятий не включают ни одного общего элемента.
Отношения совместимых понятий:
l пересечение (часть элементов объема каждого понятия входит в объем другого понятия); например, «мальчик»–«болельщик»;
l тождество (полное совпадение объемов понятий);
l подчинение (объем одного понятия полностью входит в объем другого); например, «акула»–«рыба».
Отношения несовместимых понятий:
l соподчинение; например, «рыба»–«птица» (соподчинены понятию «животное»);
l противоположность (объект, не попадающий под одно понятие, может не попадать и под другое); например, «черный»–«белый»;
l противоречие (объект принадлеит объему либо одного, либо другого понятия); например, «светящийся объект»–«несветящийся объект».
Высказывание
Высказывание (суждение) — форма мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах, или отношениях.
Высказывание характеризуется своим содержанием и формой.
Умозаключение
Умозаключение — форма мышления, посредством которой из одного или нескольких высказываний, называемых посылками, мы по определенным правилам вывода получаем заключение.
С точки зрения содержания мышление может давать истинное или ложное отражение мира, формально же оно может быть логически правильным или неправильным.
Логические операции
Высказывание, включающее другие высказывания, называют сложным. Для образования сложных высказываний используют логические операции (связки). Рассмотрим некоторые из них (в порядке приоритета при вычислении логических выражений).
Инверсия (отрицание)
Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или Ā.
Читается «НЕ» (например, «не А»).
Конъюнкция (логическое умножение)
Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается AÙ B или A&B (знак может не указываться — AB).
Читается «И» (например, «А и Б»)
Дизъюнкция (логическое сложение)
Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается AÚ B, иногда A+B.
Читается «ИЛИ» (например, «А или Б»)
Импликация (следование)
Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
В выражениях обозначается A Þ B или A ® B.
Читается «ЕСЛИ. ТО» (например, «если А, то Б»)
Эквивалентность (равнозначность)
Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A Û B или A º B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
Таблицы истинности логических операций
Таблица истинности — таблица, в которой указаны значения логической функции для всех возможных комбинаций значений ее аргументов.
Логика как наука: понятие, объект и предмет, законы логики
Наверное, нет человека, который не использовал бы слово «логика». Умозаключения, кажущиеся нам правильными, мы называем «логичными». А если кто-то поступает странно, мы говорим, что в его действиях отсутствует логика. Но на самом деле, логика это не только разумный ход рассуждений. Это целая наука, изучающая, как из одних суждений следует истинность или ложность других. Сегодня мы поговорим о том, что она собой представляет, какие законы логики и формы логического мышления существуют, а также выясним, какие функции выполняет эта наука.
Что такое логика?
Логика – это наука о формах, приёмах и операциях мышления, позволяющих устанавливать или опровергать истинность определенных утверждений, исходя из заведомо известных фактов. Сложно сказать точно, когда она возникла. Отдельные элементы логики присутствуют в работах древнегреческих, древнекитайских и древнеиндийских мыслителей 6-5 веков до н. э., но первым её основные принципы сформулировал Аристотель в 4 веке до н. э.
Изначально она возникла как направление в философии, но со временем развилась в сложную систему знаний и стала самостоятельной научной дисциплиной – формальной логикой. От остальных наук, изучающих мышление, она отличается тем, что абстрагируется от содержания размышлений и высказываний, а изучает их структуру и внутренние закономерности.
Термин «логика» образован от греческого слова λόγος (логос – мысль, слово, причина). Сегодня у него есть два основных значения. Им может обозначаться как научная дисциплина, изучающая закономерности мыслительных процессов и логических построений, так и совокупность правил, которых необходимо придерживаться при построении непротиворечивых умозаключений.
Объект и предмет логики
Как и любая наука, логика имеет объект и предмет изучения. Объектом логики является мышление человека – отображение различных явлений и процессов в его мыслях, а также построение умозаключений на основе уже имеющихся знаний о внешнем мире. Здесь следует отметить, что мышление является объектом не только для логики, но и для большого количества других наук.
Предмет логики – это система закономерностей правильного мышления. По сути, логика изучает один аспект познавательного мышления – законы и принципы, ведущие к построению непротиворечивых умозаключений. А поскольку философия изучает все аспекты познания мира, логика является философской наукой.
Формы логического мышления
Форма мышления – это структура мысли, определяющая взаимосвязи между отдельными её элементами.
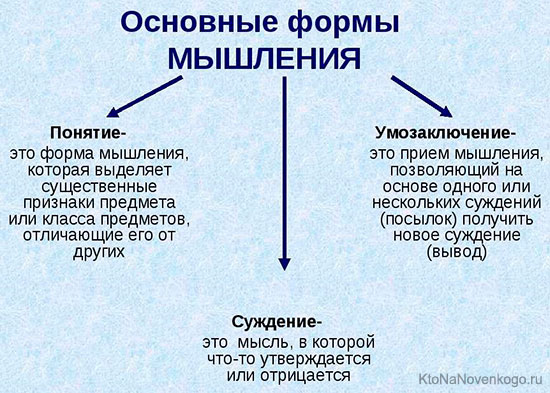
Существует три основных формы мышления:
Какие бы мысли ни крутились сейчас в вашей головы, каждая из них относится к одной из этих трёх форм. Наш жизненный опыт включает знание миллионов разных понятий, которые мы мгновенно объединяем в суждения и делаем на их основе определённые умозаключения.
Законы логики
Существует 4 закона, знание которых позволяет лучше понять, что такое логика. Придерживаясь этих законов, можно гарантированно делать правильные и логичные умозаключения при условии наличия достаточного количества точно установленных фактов:
1. Закон тождества
Суть данного закона состоит в том, что суждение сохраняет своё предметное и смысловое значение в рамках одного контекста (например, в пределах одного логического рассуждения). Иными словами, недопустимо в процессе размышления подменять одно значение понятия или суждения другим, поскольку это приведёт к ложному выводу.
К примеру, утверждение «Выучить новый язык можно, общаясь с носителями на житейские темы» истинно в отношение английского или испанского языка, но слабо применимо к языкам программирования. Подобная подмена понятий является одним из грубых нарушений закона тождества. В данном примере она очевидна, но в некоторых случаях она используется как успешный демагогический приём.
2. Закон непротиворечия
Этот закон (называемый также «законом противоречия») гласит, что два высказывания, противоречащих друг другу, не могут быть истинными одновременно. Как минимум одно из них ложно. К примеру, если на столе лежит шар, полностью выкрашенный в один цвет, утверждения «Этот шар белый» и «Этот шар чёрный» не могут быть истинными одновременно. Но они оба вполне могут быть ложными, если шар, к примеру, красный.
Есть три основных типа логических противоречий:
Контактные противоречия обычно не пытаются скрыть. Их используют сознательно, чтобы смягчить негативное высказывание («Ты хорошо справился, но это не совсем то, о чём я просил») или, наоборот, усилить его («Отлично! Ты опять всё испортил!»). Дистантные противоречия могут применять демагоги, чтобы запутать собеседника, но чаще их используют по ошибке неопытные или плохо подготовившиеся ораторы.
3. Закон исключённого третьего
Если одно суждение отрицает другое, то одно из них является ложным, а второе – истинным. Здесь важно не путать, что подразумевается под отрицанием.
К примеру, утверждения «Этот шар белый» и «Этот шар чёрный» являются всего лишь взаимоисключающими. А отрицающими друг друга являются утверждения «Этот шар белый» и «Этот шар не белый» (одно из них обязательно является истинным, какого бы цвета ни был шар).
4. Закон достаточного основания
Этот закон ввёл Готфрид Лейбниц. Его суть состоит в том, что для того, чтобы считать утверждение истинным, необходимо располагать однозначными доказательствами, исключающими другие варианты. В повседневной жизни люди пренебрегают этим законом логики чаще, чем любым другим, делая однозначные выводы по косвенным фактам.
К примеру, если в середине лета вы несколько дней подряд не видели соседа, которого обычно встречаете ежедневно, можно предположить, что он уехал в отпуск. Скорее всего, так и есть, но всё же этот вывод противоречит закону достаточного основания, поскольку нельзя исключать, к примеру, болезнь или командировку.
Нарушение законов логики
Когда законы логики нарушаются, возникают логические ошибки. Существует три основных типа логических ошибок:
Софизмы – это основной инструмент в софистике. Они используются для того, чтобы запутать собеседника, подвести его к неправильным выводам или заставить выглядеть глупо перед окружающими. Парадоксы могут возникать, в частности, когда смешиваются количественные и качественные характеристики предметов и явлений либо присутствуют неявные условия. В таком случае рассуждение, выглядящее логически правильным, может приводить к выводам, противоречащим действительности или другому логически правильному рассуждению.
В качестве примера можно привести «Парадокс кучи». Его суть состоит в следующем: если из кучи гравия убрать 1 камешек, куча останется кучей, однако если продолжать этот процесс, то в какой-то момент куча перестанет существовать. Противоречие здесь в том, что убирание одного (любого!) камня не должно приводить к исчезновению кучи. И всё же она исчезает именно от того, что из неё убирают один камень. Причина этого парадокса в том, что не сформулирована взаимосвязь между количественными и качественными характеристиками кучи.
Другой пример логической ошибки – известная апория Зенона про Ахиллеса, который никогда не догонит черепаху. Условие парадокса специально формулируется так, чтобы исключить из рассмотрения точку пути, в которой атлет обгоняет черепаху. В результате доказательство того, что он не сможет этого сделать, не противоречит законам логики. Ошибка заложена в самой формулировке задачи, в которой неявно присутствует условие «На отрезке до точки X».
Виды логики
Объясняя, что такое логика, обычно говорят в первую очередь о формальной логике. При этом существует ещё два раздела, фактически являющихся самостоятельными дисциплинами: математическая (символическая) логика и диалектическая логика. Рассмотрим каждый из разделов подробнее.
1. Формальная логика
Формальная логика – это научная дисциплина, изучающая структуру и истинность утверждений. Её создателем считается Аристотель (4 век до н. э.), рассматривавший её как возможность оперировать формальными фактами, абстрагируясь от их природы и содержания. Это позволяет обеспечить логическую правильность суждений, поскольку анализу подвергается только структура утверждения, но не его содержание.
По сути, наше мышление подчиняется формальной логике. Основываясь на имеющихся фактах, мы делаем логические выводы и принимаем решения. Однако мы не можем полностью абстрагироваться от природы и содержания суждений, кроме того, эмоции могут оказывать очень сильное влияние на наши выводы и действия. Поэтому людям свойственны нелогичные поступки.
2. Математическая логика
Изначально это была часть формальной логики, но в 19 веке она выделилась в самостоятельный раздел (при этом в ней по-прежнему соблюдаются все принципы формальной логики). Она пополнилась новыми математическими методами и специализированными нотациями. Благодаря этому символическая логика превратилась в мощный инструмент, применяемый современными науками при решении задач и доказательстве теорий.
Данная модель делает процесс познания более точным, поскольку в ней слова естественных языков с размытым смыслом заменяются формальными определениями, исключающими двусмысленность и размытость суждений. Все суждения математической логики формулируются на точном языке, не допускающем неоднозначных трактовок. Для таких языков чётко определена семантика (значения терминов) и синтаксис (совокупность формул или правил построения объектов языка).
3. Диалектическая логика
Это философская дисциплина, изучающая мышление вообще. Её основателем считается немецкий философ Георг Гегель (1770-1831). Она основывается на формальной логике, и всё же в ней учитывается содержание явлений, объектов и процессов. В ней используются такие принципы как:
Зачем нужна логика?
Главная цель логики заключается в том, чтобы обеспечить эффективный инструментарий для поиска решений и доказательств, применимый в любых сферах знаний. Благодаря логике мы можем оперировать фактами, достоверность которых установлена и доказана. Логика необходима при решении таких задач как:
Заключение
Логика – это наука о правильном мышлении и о способах рассуждения, не ведущих к ошибочным выводам. Это одна из важнейших научных дисциплин, ведь её принципами и законами пользуются все существующие науки. И даже если мы этого не замечаем, вся наша жизнь подчинена логике. Мы используем её в быту и общении, она заложена в законах, которые мы соблюдаем, без неё был бы невозможен научно-технический прогресс, достижениями которого мы пользуемся ежедневно.
Логика — это основа и законы правильного мышления
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В течение дня самого обычного человека посещает тысячи мыслей. Мы думаем о реальных объектах и явлениях, о гипотетических ситуациях (кто победит, если Годзилла сразится с Кинг-Конгом?).
Но все мысли формируются одними и теми же способами по определенным принципам. Логика как раз изучает формы, методы и законы мышления.
Что такое логика?
Этот термин имеет греческие корни. Он образовался от слова «логос», что переводится как «рассуждение, разум, мысль, смысл». Это не случайно, ведь основы современной логики заложил древнегреческий философ Аристотель.
Толковый словарь Даля дает определение: «логика — это наука здравомыслия, наука о том, как правильно рассуждать». Ее основной задачей является поиск пути перехода от предпосылок к выводу, получение достоверного знания о предмете исследования.
На самом деле, интуитивное понимание логики впитывается в нас с молоком матери. Маленький ребенок рассуждает: «Если не слушаться родителей, можно понести наказание». С детства мы учимся строить свои высказывания правильным образом, делать верные выводы, поступать логично – адекватно ситуации.
Толковый словарь Ожегова предлагает 3 значения для слова «логика»:
Основы логики — формы логического мышления
Форма мышления – это оболочка для наших мыслей, способ по которому они строятся.
Существует всего 3 формы:
Все бесконечное пространство мыслей выражается этими тремя формами.
В нашей голове хранятся миллиарды понятий, которые мы объединяем в суждения, а потом делаем из них умозаключения. И все за доли секунды, даже не осознавая этого.
Законы логики (логического познания)
Законы логики — это принципы, следуя которым из истинных суждений можно гарантированно извлечь правильный вывод.
Существуют 4 закона. Порой их нарушают случайно, тогда получается ошибочное умозаключение — паралогизм. Иногда специально, с целью запутать собеседника и подвести его к ложной мысли. Тогда возникают софизмы – недостоверные выводы, которые кажутся логически правильными.
Закон тождества
Для тех, кто прогуливал в школе математику, уточню: тождество — это равенство.
Звучит закон так: понятие должно сохранять свой изначальный смысл на всем протяжении логического рассуждения.
Язык — многогранен, почти у любого слова есть несколько смыслов. Если в процессе подменить одно значение другим, получится ложный логический вывод.
Покажу на примере известной шуточной загадки: «Зачем вода в стакане?». Конечно, чтобы ее выпили. Но нет, она за стеклом. Тут как раз идет игра смыслов, нет тождества (однозначности). Понятия нельзя смешивать понятия и обязательно нужно избегать двусмысленности.
Закон непротиворечия
Два высказывания, которые несовместимы друг с другом, не могут быть одновременно истинными. Одно из них — ложное, а, возможно, и оба.
Вот Вася говорит, что Петя украл яблоко. Петя утверждает, что это сделал Вася. Эти высказывания противоречат друг другу. Значит, они не могут быть одновременно истинными. Но оба утверждения способны оказаться ложными, если есть третий вариант — на самом деле яблоко просто упало и закатилось под стол.
Логические противоречия бывают:
Контактные противоречия сразу бросаются в глаза, а вот дистантные отследить сложно. Например, неопытный оратор начинает речь с одной идеи, потом путается и в конце сам себя опровергает.
Закон исключенного третьего
Если из двух суждений одно является отрицанием другого, то они не могут быть одновременно ложными. Хотя бы одно должно быть истинным.
Этот закон тесно связан с предыдущим. Они похожи, но есть разница. Здесь рассматриваются высказывания, отрицающие друг друга («А» и «не А»), а не противоречия.
Вот пример: Вася говорит, что Петя украл яблоко. Петя утверждает, что он этого не делал. Тут нет никакого третьего варианта, одно из высказываний должно быть истинным. Это и есть пример использования закона исключенного третьего.
Закон достаточного основания
Всякое утверждение, чтобы считаться истинным и справедливым, должно быть доказано. Подтверждение можно получить эмпирическим (опытным) или теоретическим способами.
Вот ученый заявляет, что есть элементарные частицы, которые могут двигаться быстрее скорости света. Но никто не поверит, пока он не предоставит достаточно доказательств.
Основатель закона — немецкий ученый Готфрид Вильгельм Лейбниц. В повседневной жизни часто встречается нарушение этого правила.
Подробнее о законах логики:
Формальная и математическая логика
Логика разделяется на 2 направления – формальное и математическое.
Формальная логика концентрируется на форме мышления, способах и методах перехода от предпосылок к правильным умозаключениям. Содержание мыслительного процесса ее не касается.
С точки зрения формальной логики, доказательство существования черных дыр ничем не отличается от обоснования необходимости взять с собой зонт в дорогу. Отцом-основателем этой ветви науки является древнегреческий мыслитель Аристотель.
Математическая логика занимается проблемой применения математических методов для решения логических задач и создания алгоритмов логического вывода.
В ней используется строгий символический язык, который позволяет уйти от проблемы нарушения закона тождества из-за ошибочного толкования отдельных терминов.
Поясним на примере:
| Символ математического языка | Значение |
|---|---|
| p | выражение «черепахи летают» |
| 0 | ложь |
| 1 | истина |
| ¬ | отрицание |
Вот так на языке математической логики можно описать выражение «черепахи могут летать»: |p|=0. А вот так выглядит фраза «черепахи не летают»: |¬p|=1.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Уметь мыслить логически — очень полезный навык, который сильно помогает в жизни. Жаль, что его почти не развивают в процессе обучения. Школьники и студенты просто зазубривают данные, не создавая логических связей между ними.
Значение логики сильно переоценивают. Многие гении часто принимали интуитивные и нелогичные решения, которые в последствии оказались судьбоносными. Не стоит возводить логику в культ.
Ну так черепахи летают или нет, что на сей счет думает математика? Я вот думаю, что летают, ведь если подбросить черепаху вверх, она будет лететь до тех пор пока не столкнется с Землей, а уберите силу тяжести и черепаха будет летать вечность.
Всё, что я понял из статьи, так только то, что никакого логического мышления у меня нет и никогда не было, вот так и живу, без логики.
Логические задачи для всех возрастов (с ответами в конце текста)
Логика — одна из главных дисциплин для развития ума и мышления, в примерах и задачах эта дисциплина входит в обязательный набор обучения детей. Разбираемся, как именно и когда начинать разбирать и решать логические задачи, как учить ребенка мыслить стройно и красиво.
Что такое логика
Древние греки называли логику «наукой о правильном мышлении», «способностью к рассуждению». Слово «логос» по-древнегречески значит «рассуждение», «мысль», «разум», «смысл». А логика подразумевает умение правильно мыслить. Она — первый шаг на пути интеллектуального размышления.
Логика учит тому, как из одних размышлений следуют другие и почему это правильно. Кто знает логику, привык логически мыслить, тот готов к спору, аргументации, отстаиванию своей точки зрения. Например, доказательства теорем в геометрии строго подчинены основным логическим операциям — к главным методам логического размышления относятся знаменитые дедукция (от общего к частному), индукция (от частного к общему) и абдукция (метод дедуктивного размышления, основанного на выдвижении гипотез и признании их истинными или ложными).
Законы логики
Общепринятые положения, которым должны удовлетворять все рассуждения
Дедукция
Метод логического размышления, позволяющий установить истинность суждения от общего к частному. Например, из истинного высказывания общего характера «Все люди смертны» и истинного высказывания частного характера «Сократ — человек» следует истинность суждения «Сократ смертен».
Дедукция — самый частый прием логического размышления. Именно им часто пользовался, к примеру, Шерлок Холмс. Этот прием используется в науке и для решения многих логических задач.
Индукция
Противоположный дедукции метод логического размышления, позволяющий установить истинность высказывания от истинного частного размышления к истинному общему.
Например, истинное высказывание частного случая «В Аргентине, Эквадоре и Венесуэле говорят на испанском языке» и истинного высказывания «Аргентина, Эквадор и Венесуэла латиноамериканские страны» следует истинное высказывание общего характера «Вероятно, во многих странах Латинской Америки говорят на испанском языке».
Важно — в индукции вывод об истинности следует на основании достаточных и всеобъемлющих данных. На основании данных недостаточных вывод может быть вероятностным. К примеру, попробуйте ответить на вопрос «Во всех ли странах Латинской Америки говорят на испанском языке?». Вывод «во всех» будет ложным — у вас недостаточно данных для такого утверждения. Вспомните Бразилию — там говорят на португальском. А умозаключение «Во многих странах Латинской Америки говорят на испанском» будет логически верным. Теперь можно перейти к решению логических задач.
Логические задачи как примеры размышлений с примерами (и ответами)
Попробуйте, пользуясь методами индукции и дедукции, решить следующие примеры (ответы на них мы дадим в конце текста). Размышляйте и проверяйте себя!
1. Все небесные тела движутся
Все планеты — это небесные тела
2. Все животные смертны
Все люди — животные
3. Ни одна рептилия не имеет меха
Все змеи — рептилии
4. Все котята игривые
Некоторые домашние животные — котята
5. Ни одна домашняя работа не весела
Некоторое чтение — домашняя работа
6. Все прилежные мальчики в этой школе рыжие
Некоторые прилежные мальчики в этой школе — отличники
7. Все кошки млекопитающие
Некоторые кошки не имеют хвоста
Правильные ответы
1. Все планеты движутся
2. Все люди смертны
3. Ни одна змея не имеет меха
4. Некоторые домашние животные игривы
5. Некоторое чтение не весело
6. Некоторые прилежные отличники в этой школе рыжие
7. Некоторые млекопитающие не имеют хвоста
Развернутые сюжетные логические задачи с ответами
Теперь давайте попробуем решить полноценные логические задачи. Ответы с объяснениями на каждую из них в конце материала.
Задача 1
Один кролик увидел 6 слонов, когда шел к реке. Каждый слон видел, как 2 обезьяны идут к реке. Каждая обезьяна держит в руках по одной черепахе.
Сколько животных идет к реке?
Задача 2
У матери Билли было пятеро детей. Первого звали Лала, второго — Леле, третьего — Лили, четвертого — Лоло. Как назвали пятого ребенка?
Задача 3
Выберите правильное утверждение: «Желток яйца белый» или «У яиц белые желтки».
Задача 4
Оно легкий, как перышко, но самый сильный человек не может задержать его больше чем на пять минут. Что это?
Задача 5
Чем больше его, тем меньше вы видите. Что это?
Задача 6
Вы можете найти ее на Меркурии, Марсе, Юпитере и Сатурне, но не на Земле или Нептуне. Что это?
Задача 7
Он любит пищу, но вода убивает его. Что это?
Задача 8
Что полно дыр, но может удерживать воду?
Задача 9
Что тяжелее — килограмм перьев или килограмм камней?
Задача 10
Вы едете на городском автобусе. На первой остановке садятся три женщины. На второй остановке одна женщина выходит, а мужчина садится. На третьей остановке садятся двое детей. Автобус синий, а на улице в декабре идет дождь. Какого цвета волосы у водителя автобуса?
Задача 11
Есть три дома. Один красный, один синий и один белый. Если красный дом находится слева от дома посередине, а синий — справа от дома посередине, то где же белый дом?
Задача 12, классическая, из мифа об Эдипе и Сфинксе
Что двигается на четырех ногах утром, двух — днем, и трех — вечером?
Задача 13
Человек шел под дождем неизвестно куда без пальто и зонта. Он промок насквозь, но ни один волосок на его голове не был мокрым. Как такое может быть?
Ответы и объяснения
Задача 1
В этой загадке много ловушек. Первая из них заключена в условии. Внимательно читайте его! Задание звучит так: сколько животных идут к реке?
К реке идут кролик, две обезьяны, каждая при этом держит в руках черепаху. К реке идут всего 5 животных, а слоны ни при чем. Итого, правильный ответ Г — к реке идут 5 животных.
Тут опять-таки ответ на загадку заключен в условиях. Внимательно перечитайте его! Пятого ребенка матери зовут Билли.
Ни то, ни другое. Яичные желтки желтые, а не белые!
Ни то, ни другое. Оба весят по килограмму!
Задача не имеет решения: нет никаких данных, которые помогли бы вам ответить на этот вопрос.
Где угодно! Скажем, в Саратове.
Человек. Время суток — это этапы человеческой жизни. В начале жизни ребенок ползает на четырех «ногах». Когда человек становится старше, он ходит на двух ногах. Позже постаревший человек будет ходить на трех «ногах» (две ноги плюс трость, чтобы помочь ему ходить).
«Мы используем только 10% своего мозга» и ещё 4 мифа, которые давно пора забыть
15 способов научить ребёнка понимать текст, запоминать новое и быть внимательнее. Тренируем эффективное чтение вместе
9 советов психолога, как развить у ребёнка силу воли. Педагог Ирина Беляева — о том, откуда берётся сила воли и почему бессмысленно тренировать её с самого рождения
Интересное на «Меле»:
Блоги
«Здесь надо спорить и рисковать»: в чём сила британского образования
Блоги
Принцип «пустой коробки». Как учителю обойтись без крика, сурового лица и наказаний
Промо
Только не дистант! 5 главных страхов родителей школьников
Подростки
«Ирония судьбы» уже надоела! Подростки — о советских фильмах и гендерных стереотипах в них
Задача про животных и реку — из разряда «подлых задач». Если ты дашь единственный ответ — легко показать, что он неправильный, независимо от того, какой он.
Кролик шёл к реке и *видел* 6 слонов. Ну и какие у вас основания считать, что слоны ни при чём? Может быть, они тоже шли к реке по той же дороге: начали позади кролика, но двигались быстрее и обогнали его (в этот момент он их и увидел). А может быть, так шли не все слоны, а только некоторые. Итого — к реке двигалось от 0 до 6 слонов.
Кажды слон видел 2 обезьян, идущих к реке. Опять-таки нигде не сказано, что эти обезьяны шли вместе, и ни из чего не следует, что это были одни и те же обезьяны. Например, возможна ситуация, когда к реке шли 4 обезьяны: 2 впереди кролика, 2 позади кролика и слонов. Один слон шёл от реки и встретил 2 «задних» обезьян, остальные слоны шли к реке и обогнали двух «передних» обезьян.
А можно ещё круче: слоны идут не к реке и не от реки, а параллельно реке, каждый на своём расстоянии от неё. К реке движутся 12 обезьян, все с одинаковой скоростью, кролик поочерёдно их догоняет. И как раз там, где он догоняет очередную пару — их путь пересекает очередной слон.
Про черепах всё совсем уж подло. Если черепаху несут, можно ли сказать, что она «идёт»? Зависит от нашего желания. Черепах можно считать, а можно не считать.
Пример на 14: к реке идёт кролик и 5 слонов (которые его обгонят). 6 слон идёт от реки, в противоположном направлении. Впереди слонов со скоростью кролика идут 2 обезьяны (каждый из 5 слонов их обгонит), позади слонов идут другие 2 обезьяны (шестой слон их встретит). Черепахи считаются. 1+5+2+2+2+2 = 14
Пример на 11: Обезьян всего 2 (обе впереди кролика), черепахи считаются, к реке идут все 6 слонов (которые обгонят кролика и обезьян). 1+2+2+6 = 11.
Пример на 8: Обезьян всего 2, черепахи считаются, к реке идут 3 слона (которые обгонят кролика и обезьян), от реки идут другие 3 слона (которые встретят кролика и обезьян). 1+2+2+3 = 8. Ну или можно черепах не считать, а слонов поделить не 3-3, а 5-1.
Вообще, можно соорудить пример на 1+1+12+12 = 26 животных — и этот ответ будет ровно настолько же соответствовать условиям задачи, что и «правильный» 5.