Что это за теория струн
Что такое теория струн? Простой обзор
Теория струн в настоящее время стала самой противоречивой концепцией в физике, целью которой является объединение двух столпов физики 20-го века: теории относительности Эйнштейна и квантовой механики. Проще говоря, это всеобъемлющая структура, которая может объяснить всю физическую реальность (если она доказана).
Основная идея теории струн
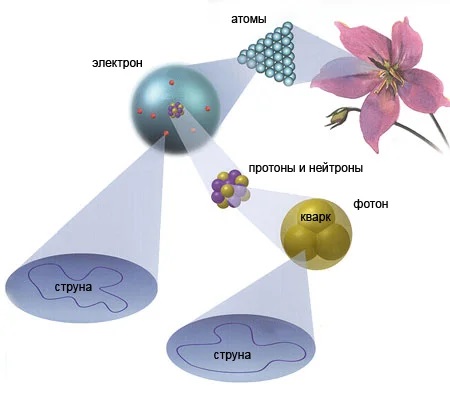
Выбери что-нибудь вокруг себя. Допустим, вы взяли яблоко со стола. Из чего сделано яблоко? Ну, чтобы ответить на этот вопрос, вам нужно заглянуть в него.
Если вы продолжите увеличивать его, рано или поздно вы начнете видеть молекулы. Но это не конец истории, если вы еще больше увеличите их и сделаете их достаточно большими, вы начнете видеть атомы.
Атомы не являются концом истории, потому что, если вы увеличите масштаб, вы увидите электроны и ядра. Ядро само состоит из протонов и нейтронов. Если вы возьмете одну из этих частиц (скажем, нейтрон) и увеличите ее, вы найдете еще больше крошечных частиц внутри, называемых кварками.
Теперь это то, где традиционная идея останавливается и теория струн приходит, предполагая, что внутри этих крошечных частиц есть что-то еще.
Обычная идея гласит, что внутри кварков нет ничего, но теория струн гласит, что вы найдете крошечную нитку, похожую на струну. Они похожи на струну на скрипке: когда вы отрываете струну, она вибрирует и создает небольшую музыкальную ноту.

Однако крошечные струны в теории струн не дают музыкальных нот. Вместо этого, когда они вибрируют, они сами производят частицы. Каждый тип вибрации соответствует различным частицам.
5 основных элементов теории струн
1. Дополнительное измерение
На данный момент теория струн является простой идеей. Нет прямых экспериментальных доказательств того, что это правильное описание природы.
Теория струн требует от нас принять существование дополнительного измерения во вселенной. В настоящее время мы живем в трех пространственных измерениях, но теория струн требует более шести высоких измерений в дополнение к четырем общим измерениям (3D + время), чтобы иметь смысл.
2. Суперсимметрия
Во Вселенной существует два основных класса элементарных частиц: бозоны и фермионы. Теория струн предсказывает, что между этими двумя частицами существует связь, называемая суперсимметрией, при которой для каждого фермиона должен существовать бозон, и наоборот.
Принцип суперсимметрии был открыт вне теории струн. Однако его включение в теорию струн позволяет определенному члену в уравнениях вычеркнуть и придать смысл. Без этого принципа уравнения теории струн приводят к физическим несоответствиям, таким как воображаемые уровни энергии и бесконечные значения.
Другими словами, объединение идеи суперсимметрии с теорией струн дает лучшую теорию, теорию суперструн.
Физики надеются, что эксперименты с ускорителями частиц и астрономические наблюдения позволят выявить несколько суперсимметричных частиц, что обеспечит поддержку теоретических основ теории струн.
3. Объединение сил
Современная физика имеет два совершенно разных закона: общая теория относительности и квантовая механика. Относительность изучает большие объекты в масштабе планет, галактик и вселенной, в то время как квантовая механика имеет тенденцию изучать крошечные объекты в природе на самых маленьких масштабах энергетических уровней атомов и субатомных частиц.
Не совсем понятно, как гравитация влияет на мельчайшие частицы. Теории, которые стремятся описать гравитацию в соответствии с принципами квантовой механики, называются теориями квантовой гравитации, и одной из наиболее многообещающих из всех таких теорий является теория струн.
4. Открытые и закрытые струны
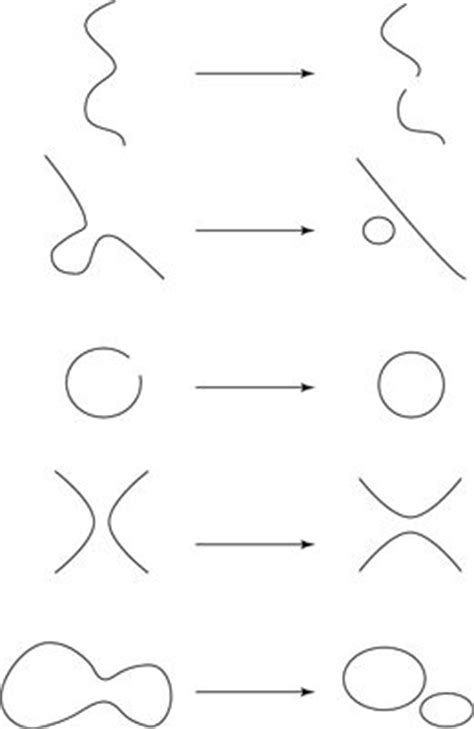
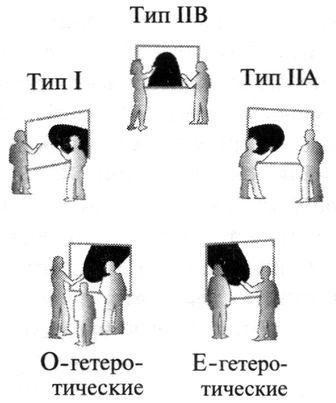
5 фундаментальных взаимодействий струны типа I
Струны в теории струн имеют две формы: открытые и закрытые струны. Две открытые струны могут соединяться с обоих концов, образуя закрытую струну. Или несколько открытых струн могут присоединиться к одному концу, чтобы сформировать новую открытую струну.
Такие струны, известные как струны типа I, могут проходить через 5 основных типов взаимодействий. Эти взаимодействия зависят от способности струны соединять и разделять концы концов.
Ученые считают, что у замкнутых струн есть особые атрибуты, которые могут описывать гравитацию в квантовой механике.
5. М-Теория
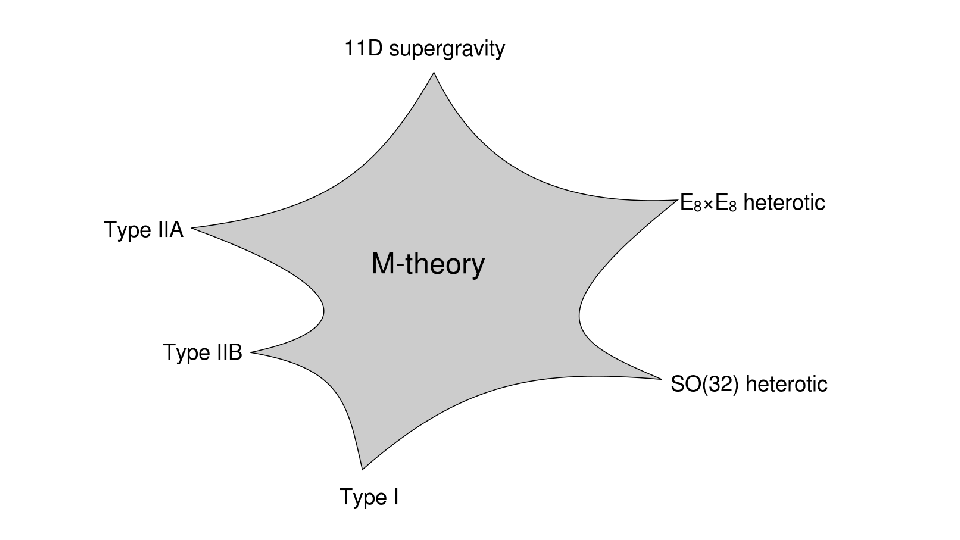
Связь между M-теорией, теориями суперструн и 11D супергравитацией | Wikimedia
Со временем ученые придумали пять различных версий теории суперструн: Тип I, Тип IIA, Тип IIIB и две версии теории гетеротических струн.
Однако в 1995 году американский физик-теоретик Эдвард Виттен объединил все пять теорий в одну 11-мерную теорию, называемую М-теорией. Это может обеспечить основу для построения единой теории всех фундаментальных сил во Вселенной.
Кто открыл теорию струн?
Теория струн взята из теории S-матриц, исследовательской программы, начатой Вернером Гейзенбергом в 1943 году. Целью этой программы было заменить локальную квантовую теорию поля как основной принцип физики элементарных частиц.
Ускорители частиц 1950-х и 60-х годов в изобилии производили адроны. Физики изобрели множество различных моделей для описания структуры спинов и масс этих сильно взаимодействующих частиц (состоящих из кварков).
Итальянский физик-теоретик Габриэле Венециано сыграл главную роль в разработке этих ранних моделей. Он сформулировал основы теории струн в 1968 году, когда обнаружил, что крошечные струны могут описывать взаимодействия адронов.
Он также опубликовал статью в 1991 году, в которой описывается, как инфляционная космологическая модель может быть получена из теории струн.
Сегодня, благодаря совместным усилиям многих исследователей, теория струн превратилась в широкую и разнообразную тему, связанную с чистой математикой, космологией, физикой конденсированного состояния и квантовой гравитацией.
Является ли теория струн теорией всего?
Это также дало новые идеи в отношении кварк-глюонной плазмы и дал много результатов, некоторые из которых могут показаться непонятными или абсурдными. Например, теория струн допускает около 10500 вселенных или обширную мультивселенную. Это одна из причин, она столкнулась с многочисленными неудачами в прошлом.
Почему теория струн важна?
Хотя теория струн до сих пор не дала каких-либо проверяемых экспериментальных предсказаний, математика в теории струн сработала. И именно поэтому это чрезвычайно полезно.
За последние несколько десятилетий теория струн предложила несколько убедительных и достоверных решений.
Исследователи также установили связь между рамками квантовой теории поля и теории струн, которая называется AdS / CFT-соответствием.
Мы еще не знаем, какова истинная природа реальности, но мы будем продолжать копать, пока не узнаем.
Эволюция теории струн до М-теории
Доброго времени суток, уважаемое хабрасообщество. После моего долгого отсутствия я решил вновь взяться за перо клавиатуру. Сегодня мы попробуем проследить эволюцию теории струн до М-теории, и найти ответы на вопросы: что подтолкнуло ученых к развитию данной теории, с какими проблемами им пришлось столкнуться, и над чем сейчас ломают головы лучшие умы человечества.
Теория струн
При дальнейших проверках этот факт получил подтверждение, интересно было и то, что ранее данная функция в основном применялась при описании колебаний натянутых струн.
При виде всего этого исследователи задались резонным вопросом: «А что, если элементарные частицы вовсе и не частицы, а микроскопические тончайшие струны, а то, что мы наблюдаем на практике — это не траектория движения частицы, а траектория колебания, проходящего по этой струне?». При том, характер колебания и указывает, какая частица перед нами: один вид колебания (колебательная мода) — одна частица, другой вид — другая.
Первые же исследования показали, что теория струн достигает значительных успехов в описании наблюдаемых явлений. Одна из мод колебаний струны может быть идентифицирована как гравитон. Другие колебательные моды проявляют свойства фотонов и глюонов.
Не без оснований казалось, что теория струн, способна свести все четыре фундаментальных взаимодействия Вселенной к одному — колебанию одномерной струны с соответствующим переносом энергии. При этом теория струн так же позволяет объяснить основные константы микромира с математической точки зрения. Становилось понятно, почему, например, массы элементарных частиц именно такие, какие есть.
Кроме того, теория струн давала надежду на объединение ОТО (общая теория относительности) и квантовой механики в рамках одной теории. При расчётах выяснилось, что собственные колебания струн способны гасить и уравновешивать квантовые флуктуации и тем самым устранить возмущения на микроскопическом уровне, из-за которых ОТО и квантовую механику никак не удавалось подружить.
Однако, при более глубоких исследованиях и проверках теории выявились серьёзные противоречия следствий с экспериментальными данными. Например, в теории струн обязательно присутствовала частица — тахион (квадрат массы которой меньше нуля, и движущаяся с скоростью большей скорости света) — как одна из колебательных мод струны, что подразумевало под собой нестабильное состояние струны и явно показывало, что теория струн требует модификации.
Теория суперструн
В 1971 году была создана модифицированная теория струн под названием «теория суперструн».

На данный момент считается, что элементарные частицы могут иметь только полуцелый или целочисленный спины. Бозонами называются те частицы, которые имеют целочисленный спин. Фермионы — частицы, у которых спин полуцелый. Исходя из этого, первая версия теории струн описывала только бозоны, из-за чего она также называлась как «бозонная теория струн». Теория суперструн же включала и фермионы — при таком подходе проблема наличия тахионов, как и множество других противоречий в теории разрешались!
Но не обошлось без новых проблем. В теории суперструн получалось, что для каждого бозона должен существовать соответствующий фермион, то есть между бозонами и фермионами должна существовать определённая симметрия. Такой вид симметрии предсказывался и раньше — под названием «суперсимметрия». Но экспериментально существование суперсимметричных фермионов не было подтверждено. Объяснялось это тем, что по расчётам, суперсимметричные фермионы должны обладать огромной для микромира массой, и потому в обычных условиях их не получить. Для того, чтобы зарегистрировать их, нужны огромные энергии, которые достигаются при столкновении лёгких частиц на почти световых скоростях.
Суперсимметричные фермионы и сейчас пытаются зарегистрировать в экспериментах на Большом адронном коллайдере, но пока безуспешно.
Многомерная Вселенная
В то же время уравнения теории суперструн никак не хотели согласовываться с квантовой теорией, выдавая в результате отрицательные или бо́льше единицы вероятности.
Чтобы были понятны предпосылки дальнейшего развития теории, совершим небольшой экскурс в историю. В далёком 1919 году немецкий математик Калуца прислал Эйнштейну письмо, где изложил свою теорию в которой делал допущение, что на самом деле Вселенная может быть четырёхмерной в пространстве, и в доказательство своих слов приводил свои расчёты, из которых получалось, что при таком условии ОТО замечательно согласовывается с теорией электромагнитного поля Максвелла, чего невозможно достичь в обычной трехмерной Вселенной. Современники высмеяли теорию, вскоре и Эйнштейн, изначально заинтересовавшийся теорией, разочаровался в ней.
В 1926 году физик Оскар Клейн тоже заинтересовался работами Калуцы и усовершенствовал его модель. По Клейну получалось, что дополнительное измерение действительно может существовать, но оно находится в «свёрнутом» и зацикленном на самом себе виде. Причём свернуто четвёртое измерение очень туго — до размеров элементарных частиц, поэтому мы его и не замечаем. Теория получила название пятимерного мира Калуцы — Клейна (четыре измерения в пространстве + время), но и она пробыла в забвении вплоть до 80-х годов 20 века.
Ученые в попытке объяснить несоответствия теории струн с квантовой механикой выдвинули предположение, что проблемы в расчётах были из-за того, что струны в нашей теории могут колебаться всего лишь в трёх направлениях, которыми располагает наша Вселенная. Вот если бы струны могли бы колебаться в четырёх измерениях…
Расчёты показали, что и в этом случае проблемы остаются, но зато число противоречий в уравнениях уменьшаются. Исследователи продолжали увеличивать число измерений, пока не ввели целых 9 измерений в пространстве, при которых, наконец-то, теория суперструн сошлась с квантовой механикой и ОТО. Этот момент вошел в историю как «первая революция в теории струн». Именно с этого момента начали раздаваться возгласы, что на самом деле мы живём в десятимерной Вселенной — одно измерение во времени, три знакомых нам измерения развернуты до космических размеров, а остальные шесть свернуты в микроскопических масштабах и потому незаметны.
С практической точки зрения ни подтвердить, ни опровергнуть экспериментально это на данный момент невозможно, так как речь идёт о таких малых масштабах струн и свернутых измерений, которые недоступны для фиксации современной аппаратурой.

М-теория
Лишь в середине девяностых годов прошлого века произошла так называемая «вторая революция в теории струн». Эдвард Виттен выдвинул гипотезу, что различные суперструнные теории представляют собой различные предельные случаи неразработанной пока 11-мерной М-теории.
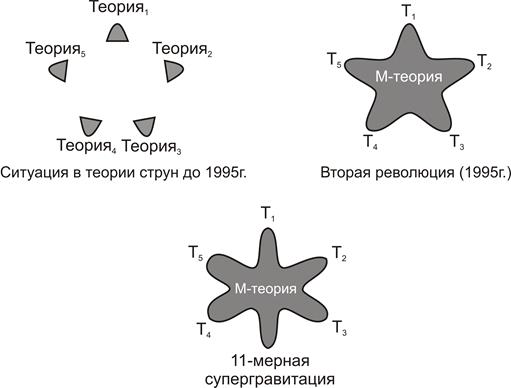
При всем при этом М-теория при низких энергиях аппроксимируется супергравитацией в одиннадцати измерениях. Связь с гравитацией делает М-теорию претендентом на то, чтобы стать связующей теорией между всеми фундаментальных взаимодействий во Вселенной, или другими словами — «Единой теорией всего».
Всё это из-за того, что свойства частиц считаются способом колебания струн, а возможные способы колебания струн зависят от точной геометрии дополнительных измерений. Существующим приближенным уравнениям удовлетворяет огромное количество разных геометрий. То есть эти уравнения были бы справедливы не только в нашем мире, но и в огромном количестве других миров, а возможно — в любом мире. Будь эти приближенные уравнения окончательными, теорию можно было бы признать нефальсифицируемой по Попперу, то есть ненаучной теорией. А так — нахождение точных уравнений, возможно, всё ещё расставит по своим местам.
В данный момент развитие М-теории осложняется еще и тем, что уравнения её описывающие настолько сложны, что ученые большей частью оперируют только их приближёнными формами, что не ведёт к повышению точности результатов. Более того, часто складывается такая ситуация, что для решения этих уравнений даже соответствующих математических методов не создано, что также создает существенные проблемы. В последнее время там где физика упирается в тупик, на самом деле часто в тупик упирается именно математика. Некоторые ученые говорят, что заметное развитие М-теория получит, только если случится «математический прорыв».
Теория струн и, в частности, М-теория, сегодня является одним из самых динамично развивающихся направлений современной физики. И хотя часть ученых из-за фундаментальных проблем довольно скептически относится к тому, что данная теория в конце концов приведет к физической теории, описывающей наш реальный мир. Существенная часть исследователей не оставляет своих надежд и верит, что в один прекрасный день М-теория таки оформится в элегантную и математически изящную Единую теорию всего.
Надеюсь, что данная статья не оставила Вас равнодушными, и буду очень рад если Вы решите, что не зря потратили время за чтением.
На пути к теории струн
Эта статья является второй частью конспекта книги «Скрытая реальность: Параллельные миры и глубинные законы Космоса».
Современная космология, от Большого взрыва до инфляции, ведет свое начало из общей теории относительности Эйнштейна. В новой теории гравитации Эйнштейн отбросил общепринятое представление о жестком и неизменном пространстве и времени; перед наукой предстал динамический космос. С накопленным к 1920-м годам математическим арсеналом и геометрической интуицией он приступил к развитию единой теории поля.
Под единой теорией поля Эйнштейн подразумевал некую схему, которая позволит включить все силы природы в единую и самосогласованную математическую модель. Но десятилетия напряжённой работы Эйнштейна в направлении объединения не оказали в то время значительного влияния — цель была великой, но для неё не пришло ещё время. Позднее другие исследователи подхватили идею единой теории. Наиболее успешная схема объединения получила название теория струн.
Краткая история объединения
Когда Эйнштейн размышлял об объединении, науке были известны две силы: гравитация, описываемая его собственными уравнениями, и электромагнетизм, описываемый уравнениями Максвелла. Эйнштейн предполагал объединить две теории в единую математическую конструкцию, которая сочленила бы действие всех сил в природе.
Цель была весьма амбициозна, и Эйнштейн отнёсся к ней очень серьёзно. У него была уникальная способность полностью отдаваться задаче, которую он перед собой поставил, и последние тридцать лет своей жизни он полностью посвятил проблеме объединения. Однако его последние вычисления не пролили больше света на вопрос объединения.
После смерти Эйнштейна работа над единой теорией практически прекратилась. Многие физики переключились на изучение микромира, руководствуясь квантовой механикой. При этом делались успехи в раскрытии тайны атома и использовании его скрытой мощи.
Давайте рассмотрим этот вопрос подробнее. Глэшоу, Салам и Вайнберг предположили, что электромагнитное и слабое взаимодействия являются проявлениями единого электрослабого взаимодействия. Электрослабая теория была подтверждена в экспериментах на ускорителе в конце 1970-х и начале 1980-х годов. Глэшоу и Джорджи пошли дальше и предложили, что электрослабое и сильное взаимодействия являются проявлениями ещё более фундаментального взаимодействия, в рамках подхода, который был назван великим объединением. Однако простейшая версия великого объединения была отброшена, когда учёным не удалось экспериментально подтвердить одно из предсказаний — что протоны должны время от времени распадаться. Тем не менее есть много других вариантов великого объединения, которые пока экспериментально не отвергнуты, например, потому, что предсказываемая ими скорость распада протона настолько мала, что чувствительность современного экспериментального оборудования недостаточна для обнаружения распада. Однако даже если великое объединение не подкрепляется экспериментальными данными, уже нет никаких сомнений, что три негравитационных взаимодействия могут быть описаны на едином математическом языке квантовой теории поля.
Всё это являлось впечатляющим продвижением к единой теории, однако на таком обнадёживающем фоне возникла досадная проблема. Когда учёные применили методы квантовой теории к четвёртой силе в природе — гравитации, оказалось, что математика просто не работает. Как бы успешно ни работали общая теория относительности и квантовая механика на своих естественных масштабах, на больших и малых расстояниях, бессмысленный результат, полученный при попытке их объединения, означал глубокую трещину в понимании законов природы.
В середине 1980-х годов произошёл следующей ключевой скачок. Новая теория, теория суперструн, завладела умами физиков по всему миру. Она смягчила разногласия между общей теорией относительности и квантовой механикой и дала надежду, что гравитация может быть встроена в объединённый квантово-механический каркас. Была развита впечатляющая и изощрённая математическая структура, но многое в теории суперструн оставалось неясным.
Открытие теории суперструн дало толчок к развитию других, тесно связанных теоретических подходов, направленных на поиски единой теории фундаментальных взаимодействий. В частности, суперсимметричная квантовая теория поля и её гравитационное расширение (супергравитация) глубоко изучались в середине 1970-х годов. Суперсимметричная квантовая теория поля и супергравитация основаны на новом принципе суперсимметрии, который был открыт в рамках теории суперструн, но эти подходы подключают суперсимметрию к обычным теориям точечных частиц.
Позже начиная с середины 1990-х годов, попытки теоретиков распутать эти загадки неожиданно привели теорию струн к сюжету с мультивселенными. Учёным давно было известно, что математические методы, применяемые при анализе теории струн, используют множество приближений, а потому их можно усовершенствовать. Когда была сделана часть уточнений, учёные осознали, что соответствующий математический аппарат ясно указывает, что наша Вселенная является, возможно, частью некоторой мультивселенной.
Квантовые поля
Начнем с рассмотрения традиционной квантовой теории поля.
В классической физике поля описываются как нечто типа тумана, который пронизывает область пространства и может переносить возмущения в виде ряби и колебаний. В квантовой механике понятия поля приводит к квантовой теории поля. Квантовая неопределенность заставляет значение поля в каждой точке случайно колебаться. Подобно воде, состоящей из молекул H2O, квантово-механическое поле состоит из бесконечно малых частиц – кванты поля. Но как бы не представлять частицы в рамках квантовой теории поля они математически описываются как крохотные точки, не имеющие пространственного размера и внутренней структуры.
Осведомлённый читатель может не согласиться с утверждением, что каждое поле ассоциируется с частицей. Более точное утверждение звучит так: малые флуктуации поля около локального минимума его потенциала обычно интерпретируются как возбуждения частиц. Этого определения будет достаточно для наших обсуждений. К тому же осведомлённый читатель заметит, что локализация частицы в точке сама по себе является идеализацией, потому что для этого потребуется — из принципа неопределённости — бесконечный импульс и энергия. Опять же суть в том, что в квантовой теории поля нет, в принципе, предела того, как можно локализовать частицу.
Вера физиков в квантовую теорию поля обусловлена одним существенным фактором: ни один эксперимент не противоречит её предсказаниям. Наоборот, данные подтверждают, что уравнения квантовой теории поля описывают поведение частиц с изумительной точностью. После такого успеха можно ожидать, что квантовая теория поля является математическим фундаментом для понимания всех сил в природе. В результате упорного труда многих из физиков к концу 1970-х было установлено, что слабое и сильное ядерные взаимодействия действительно прекрасно описываются квантовой теорией поля.
Однако многие из физиков быстро пришли к выводу, что ситуация с четвёртым взаимодействием в природе — гравитацией, гораздо тоньше. Как только уравнения общей теории относительности объединяются с уравнениями квантовой теории, математика начинает бунтовать. Совместное использование уравнений для вычисления квантовой вероятности некоторых физических процессов — таких как вероятность того, что два электрона оттолкнутся друг от друга — как правило, приводит к ответу бесконечность. Но вероятности бесконечными быть не могут. По определению значение вероятности должно находиться между 0 и 1 (между 0 и 100, если считать в процентах). Бесконечная вероятность шлёт очевидный математический намёк: совместное использование уравнений бессмысленно.
Физики выяснили, что проблема кроется в дрожании и флуктуациях из-за квантовой неопределённости. Математические методы квантовой теории поля были разработаны для анализа флуктуаций сильных, слабых и электромагнитных полей, но, при их применении к гравитационному полю — полю, которое определяет кривизну пространства-времени, — оказалось, что они бесполезны. Целое поколение физиков боролось с квантовыми флуктуациями, и к началу 1970-х годов были развиты математические методы, адекватно описывающие квантовые свойства негравитационных полей. Однако флуктуации гравитационного поля качественно другие. Они больше похожи на землетрясение. Поскольку гравитационное поле вплетено в саму ткань пространства-времени, квантовые флуктуации сотрясают всю его структуру вдоль и поперёк. Математические методы, используемые для анализа таких всеобъемлющих квантовых флуктуаций, перестают работать.
В течение многих лет физики смотрели сквозь пальцы на эту проблему, потому что она возникает только при весьма экстремальных условиях. Гравитация вступает в игру, когда объекты очень массивны, а квантовая механика — когда их размер очень мал. Редко бывает, чтобы предмет был одновременно и массивный, и малым. Однако подобные ситуации возникают. Когда гравитация и квантовая механика применяются для описания или Большого взрыва, или чёрных дыр, то есть когда действительно огромная масса вещества сжимается до небольших размеров, математические методы перестают работать.
Однако в середине 1980-х годов в физическом сообществе поползли слухи, что в направлении объединения произошёл серьёзный теоретический прорыв в рамках подхода, названного теорией струн.
Теория струн
Хотя теория струн имеет репутацию сложной теории, её основная идея очень простая. Стандартная точка зрения, до теории струн, состояла в том, что фундаментальные составляющие являются точечными частицами — точками без внутренней структуры, — которые описываются уравнениями квантовой теории поля. Теория струн бросает вызов такому представлению, утверждая, что частицы не являются точечными. Вместо этого, предлагается рассматривать их как крошечные, струноподобные вибрирующие нити.
При более детальном рассмотрении, говорит теория, вы увидите, что струны в частицах разного типа неразличимы, но вибрируют они по-разному. Электрон менее массивен чем кварк, и согласно теории струн, это означает, что струна электрона вибрирует менее энергично, чем струна кварка. Различные свойства частиц объясняются разным вибрационным поведением нитей в теории струн, подобно тому как разные вибрации гитарных струн порождают звучание разных музыкальных нот.
Струны, точки и квантовая гравитация
Следует подчеркнуть три особо важных момента.
Во-первых, когда учёные физики предлагают модель описания природы с помощью квантовой теории поля, они также выбирают поля, которые войдут в теорию. Этот выбор диктуется экспериментальными ограничениями, а также теоретическими предпосылками. Главным примером является Стандартная модель. Рассматриваемая как венец достижений физики частиц XX столетия благодаря своей способности правильно описывать большое количество данных, собранных на ускорителях частиц по всему миру, Стандартная модель является квантовой теорией поля. Стандартная модель, безусловно, крайне успешна, но многие физики полагают, что по-настоящему фундаментальное понимание не требует такого разношёрстного набора ингредиентов. Впечатляющее свойство теории струн состоит в том, что частицы определяются самой теорией: разные типы частиц соответствуют разному вибрационному поведению струны. Тогда потенциал и перспективы теории струн заключаются в том, чтобы превзойти квантовую теорию поля путём получения всех свойств частиц математически. Теория струн строится непоследовательными приближениями к полному описанию природы. Она предлагает полное описание с самого начала.
Во-вторых, среди возможных вибраций струны есть одна, обладающая всеми нужными свойствами для того, чтобы быть квантовой частицей гравитационного поля. Исследования выявили свойства, которыми будет обладать гипотетическая частица — получившая название гравитон, — соответствующая квантовому гравитационному полю. Было показано, что гравитон должен быть безмассовым, не иметь заряда и обладать квантовомеханическим свойством, известным как спин-2.
В-третьих, как бы ни была радикальна теория струн, она идёт по протоптанному пути, известному в истории физики. Специальная теория относительности расширяет наше понимание мира высоких скоростей; общая теория относительности идёт дальше и учитывает большие массы; квантовая механика и квантовая теория поля вводят нас в мир малых расстояний. Понятия, привлекаемые этими теориями, и предсказываемые ими свойства непохожи ни на что известное ранее. Более того, если применять эти теории в привычных рамках доступных нам скоростей, размеров и масс, они сведутся к описаниям, открытым до XX столетия — к классической механике Ньютона и классическим полям Фарадея, Максвелла и других.
Теория струн могла бы претендовать на существенный отрыв от своих предшественников и отступить от нарисованной схемы ниже. Замечательно, что этого не происходит. Теория струн достаточно революционна для преодоления барьеров физики двадцатого столетия. При этом она достаточно консервативна, чтобы прошедшие три столетия открытий смогли уютно разместиться в её математическом аппарате.
Пространственные измерения
В первые годы исследований по теории струн физики столкнулись с фатальными математическими изъянами, например, спонтанное возникновение или исчезновение энергии. В 1970-х многие думали, что от теории струн необходимо отказаться. Но некоторые исследователи упорно придерживались другой точки зрения.
В результате сложных исследований было выяснено, что проблемные свойства тесно связаны с числом пространственных измерений. В уравнениях теории струн нет изъянов во вселенной с девятью пространственными измерениями и одним временным, что в совокупности составляет десять измерений.
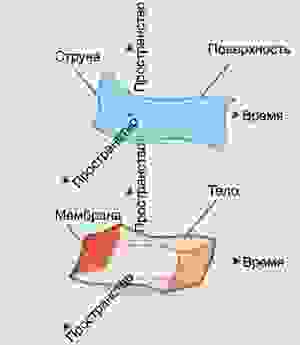
В начале XX столетия в нескольких статьях математика Калуцы и физика Клейна было высказано предположение о существовании измерений, легко ускользающих от обнаружения. Они предсказывали, что в отличие от привычных пространственных измерений, простирающихся на большие или даже бесконечные расстояния, могут существовать дополнительные измерения, настолько малые и скрученные, что их очень трудно увидеть. На рисунке поверхность высокой трубочки имеет два измерения; длинное вертикальное измерение легко увидеть, а малое круговое измерение обнаружить труднее.
Из предложения Калуцы–Клейна следует, что похожее различие между одними измерениями, большими и легко видимыми, и другими, малыми и слабо различимыми, может иметь место и для структуры самого пространства. Причина, по которой мы всё знаем о привычных трёх пространственных измерениях, может быть в том, что их протяжённость велика (может даже бесконечны). Однако если дополнительное пространственное измерение скручено и имеет чрезвычайно малый размер, то оно совершенно равноправно обычным нескрученным измерениям и при этом остаётся невидимым даже для самого мощного современного увеличивающего оборудования. Так начиналась теория Калуцы–Клейна, гипотеза о том, что наша Вселенная имеет больше трёх пространственных измерений.
Если вернуться в 1920-е годы, откуда вообще возникла такая экзотическая идея? Калуца заинтересовался этим, потому что вскоре после публикации Эйнштейном общей теории относительности ему на ум пришла одна идея. Он обнаружил, что может модифицировать уравнения Эйнштейна и применить их ко вселенной с одним дополнительным пространственным измерением. Результат изучения модифицированных уравнений оказался захватывающим. Среди модифицированных уравнений Калуца обнаружил уравнения, уже применённые Эйнштейном для описания гравитации в трёх пространственных и одном временном измерениях. Но поскольку новая формулировка включала одно дополнительное пространственное измерение, Калуца обнаружил дополнительное уравнение. Получив это уравнение, Калуца распознал в нём уравнение электромагнитного поля, обнаруженное Максвеллом полувеком ранее.
Как показал Калуца, во вселенной с одним дополнительным пространственным измерением гравитация и электромагнетизм могут быть описаны единым образом как пространственно-временные искривления. Но гравитация рябит в привычных трёх пространственных измерениях, а электромагнетизм — в четвёртом. Огромной проблемой для гипотезы Калуцы стало объяснение того, почему мы не видим четвёртое пространственное измерение. Именно тогда Калуца предложил описанное выше решение: дополнительные измерения, если они достаточно малы, могут ускользать от фиксации нашими органами чувств и оборудованием.
Однако последующие исследования показали, что программа Калуцы–Клейна сталкивается с некоторыми препятствиями, самым трудным из которых является невозможность встроить детальные свойства частиц материи, таких как электрон, в математическую структуру. В течение двух десятилетий предлагались и отвергались различные способы обойти эту проблему. Однако поскольку не было предложено ни одного подхода, свободного от этих недостатков, то к середине 1940-х годов идея объединения через дополнительные измерения практически была забыта.
Спустя тридцать лет возникла теория струн. Математический аппарат теории струн не просто разрешал существование во Вселенной дополнительных измерений, он требовал их присутствия. Теория струн возродила программу Калуцы–Клейна, и к середине 1980-х годов учёные во всём мире воодушевлённо полагали, что это только вопрос времени, когда теория струн приведёт к полному описанию всей материи и взаимодействий.
Большие надежды
В первые годы теории струн развитие происходило настолько быстро, что уследить за всеми новостями было практически невозможно. При таком возбуждении понятно, что некоторые теоретики заговорили о скорой революции в решении основных проблем фундаментальной физики: слиянии гравитации и квантовой механики, объединении всех сил в природе, выяснении происхождения Вселенной. Но более умудрённые физики полагали, что такие надежды преждевременны. Теория струн настолько насыщена, обширна и математически трудна, что спустя почти три десятилетия после первой эйфории современные учёные одолели лишь часть исследовательского пути. С учётом того, что мир квантовой гравитации в сотни миллиардов миллиардов раз меньше чем всё, что мы сегодня можем экспериментально измерить, дорога будет длинная, даже по самым скромным оценкам.
Теория струн и свойства частиц
Один из самых основных вопросов всей физики стоит так: почему частицы, которые наблюдаются в природе, являются именно такими, а не какими-нибудь другими? Интерес к этому вопросу непросто академический, он отражает очень важный факт. Если бы у частиц были другие свойства, ядерные процессы, питающие звёзды, подобные нашему Солнцу, были бы нарушены. Вселенная без звёзд была бы совсем другой. Очевидно, что без солнечного света и тепла не возникла бы сложная цепочка событий, приведшая к возникновению жизни на Земле. Поэтому возникает фундаментальный вопрос: как с помощью ручки, бумаги и, возможно, компьютера, а также руководствуясь нашим пониманием законов природы, вычислить свойства частиц и получить результаты, которые согласуются с экспериментальными данными.
В рамках квантовой теории поля ответа на этот вопрос нет и не может быть. В квантовой теории поля измеренные свойства частиц выступают в качестве исходных данных — на их основе строится и определяется сама теория.
Сможет ли теория струн справиться с этим лучше? Одна из самых красивых черт струнной теории состоит в том, что свойства частиц определяются размером и формой дополнительных измерений. Поскольку струны очень малы, они вибрируют не только в трёх привычных больших измерениях, но и в малых, свёрнутых измерениях. Колебания струн в струнной теории определяются формой скрученных измерений. Вспоминая, что вибрационное поведение струн определяет свойства частиц, такие как массу и электрический заряд, мы видим, что эти свойства диктуются геометрией дополнительных измерений. Поэтому если достоверно известно, как выглядят дополнительные измерения в теории струн, то можно легко предсказать любые свойства вибрирующих струн и, следовательно, все свойства элементарных частиц, порождённых колебаниями струны. Трудность, как и раньше, в том, что никто не знает, какова точная геометрическая форма дополнительных измерений. Уравнения теории струн накладывают математические ограничения на геометрию дополнительных измерений и требуют, чтобы они принадлежали частному классу так называемых пространств Калаби–Яу. Проблема в том, что нет какой-то одной, выделенной формы Калаби–Яу. Наоборот, эти пространства имеют разные размеры и контуры. Дополнительные измерения, различающиеся по размерам и по форме, порождают разные вибрации струн и, следовательно, разные наборы свойств частиц. Отсутствие однозначной спецификации для дополнительных измерений является главным камнем преткновения, который не позволяет струнным теоретикам делать конкретные предсказания.
В середине 1980-х годов, было известно небольшое количество пространств Калаби–Яу, поэтому можно было надеяться проанализировать каждое из них и соотнести с известной физикой. Спустя несколько лет, число пространств Калаби–Яу возросло до нескольких тысяч, что стало серьёзной задачей для обстоятельного изучения. Время шло и число страниц в каталоге пространств Калаби–Яу только увеличивалось. Теперь их больше чем песчинок на пляже. И речи быть не может о том, чтобы математически рассмотреть каждое на роль дополнительных измерений. Поэтому струнные теоретики продолжают поиск математической подсказки, которая позволит выделить из всех возможных пространств Калаби–Яу то самое, единственное.
Теория струн пока не реализовала свои возможности по объяснению свойств фундаментальных частиц. В этом отношении теория струн до сих пор не имеет особых преимуществ перед квантовой теорией поля.
Теория струн и эксперименты
Если типичная струна имеет чрезвычайно крохотный размер, то для обнаружения её протяжённой структуры — той самой характеристики, которая отличает её от частицы — потребуется ускоритель в миллионы миллиардов раз мощнее, чем БАК. Предполагая, что выдающийся технологический прорыв не предвидится, такая ситуация означает, что на сравнительно малых энергиях, достижимых на имеющихся ускорителях, струны неотличимы от точечных частиц. Экспериментальная версия упомянутого ранее теоретического факта: на низких энергиях теория струн сводится к квантовой теории поля. Таким образом, даже если теория струн и является правильной фундаментальной теорией, в широком диапазоне доступных экспериментов она будет проявляться как квантовая теория поля.
Выбор полей и кривых энергий в квантовой теории поля равносилен выбору формы дополнительных измерений в теории струн. Одна из проблем в теории струн состоит в том, что математика, которая связывает свойства частиц с формой дополнительных измерений, в высшей степени своеобразна. Поэтому работа в обратном направлении очень трудна — использование экспериментальных данных для определения конкретной формы дополнительных измерений, аналогично тому, как такие данные определяют состав полей и кривых энергий в квантовой теории поля. В обозримом будущем наиболее обещающим способом связи теории струн с экспериментальными данными будут предсказания, которые можно объяснить с помощью более традиционных методов, но для которых гораздо более естественное и убедительное объяснение возникает из теории струн.
Теория струн, сингулярность и черные дыры
В большинстве ситуаций квантовая механика и гравитация успешно игнорируют друг друга, при этом первая применяется к малым объектам, таким как молекулы и атомы, а вторая к большим объектам, соразмерным звёздам и галактикам. Однако обе теории вынуждены встречаться в мирах, известных как сингулярности. Сингулярность — это любая физическая ситуация, реальная или гипотетическая, которая настолько экстремальна (огромные массы, малый размер, гигантская кривизна пространства, проколы или разрывы в самой пространственно-временной структуре), что квантовая механика и общая теория относительности ведут себя неадекватно.
В середине 1980-х годов группа исследователей пришла к выводу, что некоторые проколы в ткани пространства, которые доставляли много хлопот уравнениям Эйнштейна, прекрасно ведут себя в теории струн. Ключ к успеху состоял в том, что струна в отличие от точечной частицы не может свалиться в такой прокол. Поскольку струна — это протяжённый объект, она может удариться о прокол, может обмотаться вокруг него либо воткнуться в него, но подобного рода умеренные взаимодействия совершенно не портят уравнения теории струн. Это важно не потому, что такие изъяны в пространстве действительно имеют место — может, да, а может, и нет, — а потому, что именно таких свойств физики хотят от квантовой теории гравитации: способности работать осмысленно в ситуации, когда по отдельности отказывают как общая теория относительности, так и квантовая механика.
В 1990-х годах было установлено, что более сильные сингулярности (известные как флоп-сингулярности), возникающие при сжатии сферической области пространства до бесконечно малого размера, тоже описываются теорией струн. Интуиция подсказывает, что струна при движении может накрутиться на такую сжатую область пространства, подобно обручу на мыльный пузырь, создавая нечто вроде кругового ограждения. Вычисления показывают, что такой «струнный щит» сводит на нет любые потенциально разрушительные последствия и гарантирует, что уравнения теории струн остаются непротиворечивыми.
За прошедшие годы исследователи показали, что множество других, более сложных сингулярностей также полностью контролируются теорией струн.
Но остаётся проблема устранения с помощью теории струн сингулярностей чёрных дыр и Большого взрыва, более суровых, чем рассмотренные ранее.
Тем не менее одно важное открытие пролило свет на теорию чёрных дыр. В 1970-х годах в работах Бекенштейна и Хокинга было установлено, что чёрные дыры обладают определённой степенью беспорядка, известной как энтропия. Беспорядок внутри чёрной дыры, согласно фундаментальным физическим законам, свидетельствует о множестве вариантов случайного размещения её внутренностей. Однако даже после долгих усилий физикам не удалось достаточно хорошо разобраться в том, как устроены внутренности чёрных дыр, не говоря уж о том, чтобы проанализировать возможные способы их размещения. Однако смешав фундаментальные ингредиенты теории струн, они построили математическую модель беспорядка чёрной дыры, достаточно простую и понятную, чтобы извлечь из неё численное значение энтропии. Полученный результат в точности совпал с ответом Бекенштейна и Хокинга. Хотя осталось много открытых вопросов, эта работа стала первым надёжным квантово-механическим анализом беспорядка чёрной дыры. Замечательный прогресс в изучении сингулярности чёрной дыры и её энтропии привёл физическую общественность к обоснованной убеждённости, что со временем оставшиеся трудности, связанные с чёрными дырами и Большим взрывом, будут преодолены.
Оценивая текущий статус теории струн, многие струнные теоретики считают, что следующий важный шаг состоит в том, чтобы придать уравнениям теории наиболее полный и точный вид. Большая часть исследований на протяжении первых двух десятилетий развития теории до середины 1990-х годов была выполнена с помощью приближённых уравнений, ибо многие полагали, что так можно выявить общие свойства теории. Однако приближённые уравнения оказались слишком грубы, чтобы дать точные предсказания. Последние открытия вывели понимание на уровень, намного превосходящий тот, что был достигнут приближёнными методами.