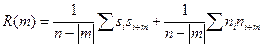Что характеризует автокорреляционная функция

Автокорреляционная функция

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Автокорреляционная функция (АКФ, ACF).

В обработке сигналов автокорреляционная функция (АКФ) определяется интегралом:

и показывает связь сигнала (функции ) с копией самого себя, смещённого на величину .

В теории случайных функций АКФ является корреляционным моментом двух значений одной случайной функции :

Здесь , а — математическое ожидание.

График автокорреляционной функции можно получить, отложив по оси ординат коэффициент корреляции двух функций (базовой и функции сдвинутой на величину ) а по оси абсцисс величину . Если исходная функция строго периодическая, то на графике автокорреляционной функции тоже будет строго периодическая функция. Таким образом, из этого графика можно судить о периодичности базовой функции, а следовательно, и о её частотных характеристиках. Это применяется для анализа сложных колебаний, например электроэнцефалограммы человека.

Содержание

Применение в технике

Корреляционные свойства кодовых последовательностей, используемых в широкополосных системах, зависят от типа кодовой последовательности, её длины, частоты следования её символов и от её посимвольной структуры.

Изучение АКФ играет важную роль при выборе кодовых последовательностей с точки зрения наименьшей вероятности установления ложной синхронизации.

Другие применения

Автокорреляционная функция играет важную роль в математическом моделировании и анализе временных рядов, показывая характерные времена для исследуемых процессов (см., например: Турчин П. В. Историческая динамика. М.: УРСС, 2007. ISBN 978-5-382-00104-3). В частности, циклам в динамике систем соответствуют максимумы на соответствующей автокорреляционной функции.

См. также

Ссылки

Полезное

Смотреть что такое «Автокорреляционная функция» в других словарях:

автокорреляционная функция — Фурье преобразование энергетического спектра заданной функции согласно теореме Винера Хинчина. [ГОСТ 24453 80] Тематики измерение лазерного излучения … Справочник технического переводчика

автокорреляционная функция — autokoreliacijos funkcija statusas T sritis automatika atitikmenys: angl. autocorrelation function vok. Autokorrelationsfunktion, f rus. автокорреляционная функция, f pranc. fonction d auto corrélation, f … Automatikos terminų žodynas

Автокорреляционная функция — 4. Автокорреляционная функция Фурье преобразование энергетического спектра заданной функции согласно теореме Винера Хинчина Источник: ГОСТ 24453 80: Измерения параметров и харак … Словарь-справочник терминов нормативно-технической документации

ФУНКЦИЯ, АВТОКОРРЕЛЯЦИОННАЯ — функция, характеризующая степень связи значений случайного процесса F(t) в моменты t1 и t2 … Большой экономический словарь

ФУНКЦИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ, КОРРЕЛЯЦИОННАЯ — см. ФУНКЦИЯ, АВТОКОРРЕЛЯЦИОННАЯ … Большой экономический словарь

корреляционная функция — Ндп. автокорреляционная функция Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание Корреляционная функция характеризует… … Справочник технического переводчика

Корреляционная функция — 24. Корреляционная функция Ндп. Автокорреляционная функция Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание.… … Словарь-справочник терминов нормативно-технической документации

АКФ — Автокорреляционная функция. В обработке сигналов автокорреляционная функция (АКФ) определяется интегралом: и показывает связь сигнала (функции ) с копией самого себя, смещённого на величину τ. В теории случайных функций АКФ является… … Википедия

Источник

Автокорреляционная функция

Введение

Корреляция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Автокорреляция уровней

Эконометрические модели, характеризующие протекание процесса во времени или состояние одного объекта в последовательные моменты времени (или периоды времени), представляют модели временных рядов. Временным рядом называется последовательность значений признака, принимаемых в течение нескольких последовательных моментов времени или периодов. Эти значения называются уровнями ряда. Между уровнями временного ряда, или ряда динамики, может иметься зависимость. В этом случае значения каждого последующего уровня ряда зависят от предыдущих. Подобную корреляционную зависимость между последовательными уровнями ряда динамики называют автокорреляцией уровней ряда.

Количественное измерение корреляции осуществляется посредством использования линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени:

. (9.1)

Если сдвиг во времени составляет всего один шаг, то соответствующий коэффициент корреляции называется коэффициентом автокорреляции уровней ряда первого порядка. При этом лаг равен 1. Измеряется же зависимость между соседними уровнями ряда. В общем случае число шагов (или циклов), на которые осуществляется сдвиг, характеризующий влияние запаздывания, также называется лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.

Динамика уровней ряда может иметь основную тенденцию (тренд). Это весьма характерно для экономических показателей. Тренд является результатом совместного длительного действия множества, как правило, разнонаправленных факторов на динамику исследуемого показателя. Довольно часто динамика уровней ряда подвержена циклическим колебаниям, которые зачастую носят сезонный характер. Иногда не удается выявить тренд и циклическую компоненту. Правда нередко в этих случаях каждый следующий уровень ряда образуется как сумма среднего уровня ряда и некоторой случайной компоненты.

В очень многих случаях уровень временного ряда представляется в виде суммы тренда, циклической и случайной компонент или в виде произведения этих компонент. В первом случае это аддитивная модель временного ряда, во втором — мультипликативная модель. Исследование временного ряда заключается в выявлении и придании количественного выражения каждой из этих компонент, после чего удается использовать соответствующие выражения для прогнозирования будущих значений ряда. Можно также решать задачу построения модели взаимосвязи двух или нескольких временных рядов.

Автокорреляционная функция

Для выявления трендовой, циклической компонент можно использовать коэффициент автокорреляции уровней ряда и автокорреляционную функцию. Автокорреляционная функция — это последовательность коэффициентов автокорреляции уровней первого, второго и последующих порядков. Соответственно график зависимости значений автокорреляционной функции от величины лага (порядка коэффициента автокорреляции) — коррелограмма. Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная.

Прежде чем пояснить это, отметим: коэффициент автокорреляции характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Если ряд имеет сильную нелинейную тенденцию, коэффициент автокорреляции может приближаться к нулю. Знак его не может служить указанием на наличие возрастающей или убывающей тенденции в уровнях ряда.

Теперь об анализе структуры временного ряда с помощью автокорреляционной функции и коррелограммы. Довольно ясно, что, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит основную тенденцию, или тренд, и, скорее всего, только ее. Если ситуация иная, когда наиболее высоким оказался коэффициент корреляции некоторого отличного от единицы порядка, то ряд содержит циклические компоненты (циклические колебания) с периодом моментов времени. Наконец, если ни один из коэффициентов корреляции не является значимым, то достаточно правдоподобны следующие две гипотезы. Либо ряд не содержит ни тренда, ни циклических компонентов, так что его структура носит флуктуационный (резко случайный) характер. Либо имеется сильная нелинейная тенденция, обнаружение которой требует дополнительных специальных исследований.

Автокорреляция связана с нарушением третьего условия Гаусса — Маркова, что значение случайного члена (случайного компонента, или остатка) в любом наблюдении определяется независимо от его значений во всех других наблюдениях. Для экономических моделей характерна постоянная направленность воздействия не включенных в уравнение регрессии переменных, являющихся наиболее частой причиной положительной автокорреляции. Случайный член в регрессионной зависимости подвергается воздействию переменных, влияющих на зависимую переменную, которые не включены в уравнение регрессии. Если значение случайного компонента в любом наблюдении должно быть независимым от его значения в предыдущем наблюдении, то и значение любой переменной, «скрытой» в случайном компоненте, должно быть некоррелированным с ее значением в предыдущем наблюдении.

Попытки вычисления коэффициентов корреляции различных порядков и тем самым формирования автокорреляционной функции являются, так сказать, непосредственным выявлением корреляционной зависимости, которое иногда приводит к вполне удовлетворительным результатам. Имеются специальные процедуры оценивания неизвестного параметра σ в выражении линейной зависимости, представляющем рекуррентное соотношение, связывающее значения случайных компонентов в текущем и предыдущем наблюдениях (коэффициент авторегрессии).

Тем не менее, необходимо иметь также и особые тесты на наличие или отсутствие корреляции по времени. В большинстве этих тестов используется такая идея: если имеется корреляция у случайных компонентов, то она присутствует также и в остатках, получаемых после применения к модели (уравнениям) обычного МНК. Не станем здесь вдаваться в подробности реализации этой идеи. Они не очень сложны, но связаны с громоздкими алгебраическими преобразованиями. Важнее иметь в виду следующее. Как правило, все или почти все они связаны с проверкой двух статистических гипотез. Нулевая гипотеза — отсутствие корреляции σ = 0. Альтернативная гипотеза либо просто состоит в том, что несправедлива гипотеза нулевая, т.е. σ ≠ 0, либо так называемая односторонняя, более точная σ > 0. Несмотря на вид второй (альтернативной) гипотезы, соответствующее распределение (используемое в критерии) зависит не только от числа наблюдений и количества регрессоров (объясняющих переменных), но и от всей матрицы коэффициентов при неизвестных в уравнениях системы.

Понятно, что невозможно составить таблицу критических значений для всех матриц, так что приходится использовать обходные способы применения таких тестов. В тесте Дарбина — Уотсона используются для этого верхняя и нижняя (две) границы, которые уже зависят только от количества наблюдений, регрессоров и уровня значимости, таким образом, их уже можно «затабулировать» (составить для них таблицы). Правда, применение их (границ) далеко не всегда просто! Все ясно, когда соответствующая статистика (эмпирическое, или рассчитанное распределение) Дарбина — Уотсона меньше нижней границы, то отвергается нулевая гипотеза и принимается альтернативная гипотеза. Если же тест больше верхней границы, то принимается первая (нулевая) гипотеза. Но если тест попадает между этими границами, ситуация становится неопределенной: непонятно как выбрать одну из двух гипотез. К сожалению, ширина этой неопределенной зоны вполне может быть довольно пространной. Естественно, что поэтому пытались и небезуспешно построить тесты, сужающие такую зону неопределенности.

Вернемся теперь к проблеме выявления основной зависимости. Для этого существуют различные методы. Это могут быть качественные методы и качественный анализ исследуемых временных рядов, в т.ч. построение и визуальный анализ графика зависимости уровней ряда от времени. Это могут быть методы сопоставления двух параллельных рядов и методы укрупнения интервалов. Поскольку они носят достаточно качественный характер, суть их понятна из названия и к тому же они приводятся в курсах статистики, не будем останавливаться на них подробно.

Источник

Автокорреляционная функция и ее применение.

Автокорреляционная функция (АКФ) характеризует степень корреляционной связи между отдельными значениями наблюдений, представленными в виде случайного процесса и расположенными на некотором удалении друг от друга.

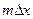
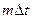
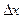
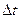
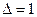
Применительно к геофизическим данным АКФ представляет характеристику связи между значениями поля, отстоящими друг от друга на m— дискретов, т.е. дискретов по x или по t. АКФ является функцией аргумента или , где — шаг по профилю, — шаг по трассе сейсмограммы, т.е. .

АКФ рассчитывается по формуле:

(4.1)

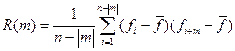
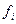
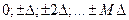
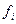
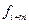
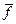
где — значение поля в i-той точке профиля (трассы, скважины); n – число точек наблюдений; m – интервал, принимающий последовательно значения , которые выражают расстояния между значениями поля и ; — среднее значение поля по профилю, трассе и т.д.

Для m=1, сумма в выражении 4.1 представляет собой сумму произведений центрированных[3], значений поля соседних точек профиля:

(4.2)

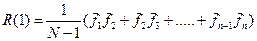
Для m=2, сумма в выражении 4.1 представляет собой сумму произведений центрированных значений поля, удаленных друг от друга на один пикет:

(4.3)

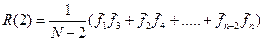
4.Два случайных процесса F₁=1, f₂,…..f_n> и F₂=1, kf₂,…..kf_n> отличающиеся только постоянным множителем k, имеют один и тот же вид нормированной автокорреляционной функции R_н(m).

5.Два случайных процесса F₁=1, f₂,…..f_n> и F₂=1+k, f₂+k,…..f_n+k> смещенные относительно друг друга на постоянную величину k, имеют один и тот же вид нормированной автокорреляционной функции R_н(m).

Анализируя выражения 4.1 и 4.5 можно сделать вывод о том, что нормированные значения автокорреляционной функции R_н.(m) есть не что иное, как коэффициент корреляции, рассчитанный для точек удаленных друг от друга на m пикетов. Таким образом, значения корреляционной функции, для конкретного аргумента m показывает насколько значения поля, удаленные друг от друга на m пикетов, коррелированны[5] между собой. Так, если R(5)=0.85, то это свидетельствует о том, что значения поля, удаленные друг от друга на 5 пикетов, в целом, достаточно коррелированны, если R(9)=0.05, то значения поля удаленные на 9 пикетов практически независимы (некоррелированны). Наконец, если, например, R(13)=-0.9, то между значениями поля, отстоящими друг от друга на 13 пикетов, существует сильная обратная корреляционная связь. Случайный процесс, для которого даже при единичном смещении R(1)

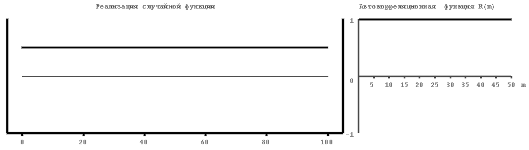
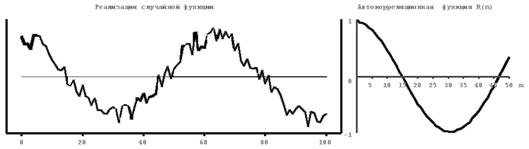
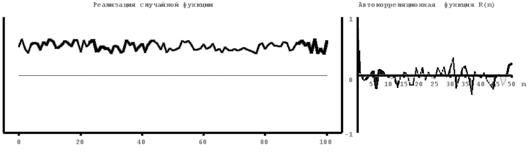
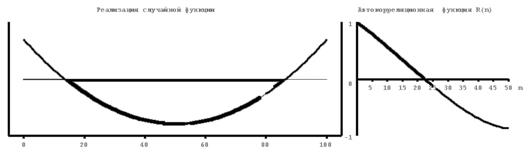
На рисунке 4.1 приведены примеры расчета нормированных автокорреляционных функций для различных случайных процессов, близких по форме к константе (1), синусоиде (2), абсолютно некоррелируемому процессу (3), квадратичной (4) и линейной (5) функциям. Из второго рисунка следует, что автокорреляционная функция периодического процесса является также периодической. При этом период автокорреляционной функции совпадает с периодом процесса. Для абсолютно некоррелируемого сигнала значения автокорреляционной функции близки к нулю при любых значениях аргумента, отличных от нуля.

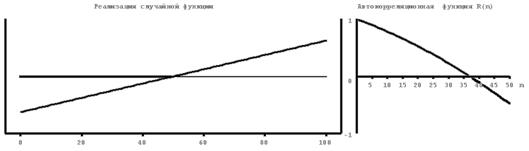Рис.4.1. Некоторые реализации случайных процессов (слева) и их автокорреляционные функции (справа). 1-константа, 2-косинусоида, осложненная помехой, 3- абсолютно некоррелируемый сигнал или «белый шум», 4 – парабола, 5-линейная функция.

Нормированные значения автокорреляционной функции постоянного процесса тождественно равны единице, так как при любых смещениях m значения случайного процесса полностью совпадают, то есть абсолютно коррелируемы.

По АКФ определяется такой важный атрибут, как интервал корреляции. Под интервалом или радиусом корреляции понимают такое расстояние между значениями поля r, начиная с которого значения поля и можно считать некоррелированными, а при нормальном законе распределения – независимыми между собой. Для оценки интервала корреляции используются разные эвристические приемы. Наиболее распространенным приемом является оценка величины r по заданному значению , где . При этом r принимается равным аргументу АКФ, m, начиная с которого выполняется соотношение .

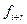
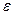
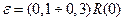
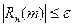
Для оценки интервала корреляции используются также соотношения:

или .

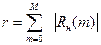
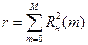
На практике, радиус корреляции оценивают по минимальному значение аргумента m, при котором автокорреляционная функция первый раз пересекает ось абсцисс.

Форма АКФ и интервал корреляции используются при решении различных задач обработки геофизических данных, из них выделим следующие:

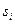
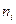
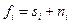
1) Оценка корреляционных свойств сигналов и помех. При отсутствии корреляции между сигналом помехой , что обычно постулируется, т.е. появление сигнала не зависит от помехи, АКФ представляется суммой АКФ сигнала и АКФ помехи, поскольку :

Из этого выражения следует, что при малой интенсивности помехи по сравнению с интенсивностью сигнала АКФ представляет оценку корреляционных свойств сигнала, и, наоборот, на интервале, где отсутствует сигнал, АКФ оценивает свойства помехи;

2) АКФ сигнала и помех является основой расчета всех оптимальных фильтров, рассматриваемых в главе VII;

3) При совпадении формы сигнала и формы АКФ помехи никакая дополнительная обработка по их разделению не внесет ничего нового, поскольку при этом частотные диапазоны сигнала и помехи полностью перекрываются между собой;

4) Разделение на однородные в статистическом отношении участки с целью геологического картирования. С этой целью используются обычно одновременно среднее значение, дисперсия и интервал корреляции, рассчитываемые в скользящих окнах;

6) Использование интервала корреляции для оценки глубины залегания h объектов по потенциальным полям .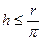

На этом простом соотношении между глубиной h и интервалом корреляции r, точно выполняемом для объектов в виде цилиндров бесконечного простирания, основаны приемы гравитационного, предложенного А.М.Петрищевским, и корреляционного, предложенного А.В.Петровым, зондирований потенциальных полей;

7) Оценка длительности реализации, например, длины профиля, для которой рассчитывается АКФ. В общем случае дисперсия АКФ определяется выражением 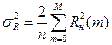, из которого следует возможность оценивания длительности самой реализации n.

Дата добавления: 2016-01-16 ; просмотров: 3862 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник