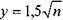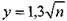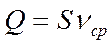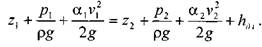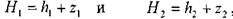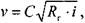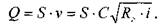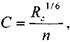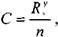Что характеризует безнапорный поток
Безнапорный поток
Безнапорный поток, самотёк (англ. gravity flow, free water ; нем. Freispiegelfluss m, druckloser Selbstfluss m, Fliessen n durch Eigengefälle ) – поток, имеющий место при безнапорном движении – движется без напора, то есть под действием собственного веса, не заполняя весь объём трубы, тунеля.
При нефтедобыче безнапорный поток — это такой поток, пъезометрическая линия которого сходится со свободной поверхностью потока, то есть расположена ниже верхней границы продуктивного пласта. Безнапорный поток может быть открытым или закрытым.
Характеристики потока
К основным характеристикам потока относят:
См. также
Литература
Полезное
Смотреть что такое «Безнапорный поток» в других словарях:
безнапорный поток — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN free water … Справочник технического переводчика
безнапорный трубопровод — Трубопровод, в котором осуществляется безнапорное движение жидкости, при котором поток ограничен сверху свободной поверхностью, давление на которую одинаково. [ГОСТ 15528 86] Тематики измерение расхода жидкости и газа Обобщающие термины… … Справочник технического переводчика
безнапорный водный поток — beslėgė vandens tėkmė statusas Aprobuotas sritis melioracija apibrėžtis Vandens tėkmė vandentakiu esant laisvajam paviršiui. atitikmenys: angl. free surface flow rus. безнапорный водный поток šaltinis Lietuvos Respublikos žemės ūkio ministro… … Lithuanian dictionary (lietuvių žodynas)
Безнапорный трубопровод — 1. Безнапорный трубопровод Трубопровод, в котором осуществляется безнапорное движение жидкости, при котором поток ограничен сверху свободной поверхностью, давление на которую одинаково Источник: ГОСТ 15528 86: Средства измерений расхода, объема… … Словарь-справочник терминов нормативно-технической документации
СО 34.21.308-2005: Гидротехника. Основные понятия. Термины и определения — Терминология СО 34.21.308 2005: Гидротехника. Основные понятия. Термины и определения: 3.10.28 аванпорт: Ограниченная волнозащитными дамбами акватория в верхнем бьефе гидроузла, снабженная причальными устройствами и предназначенная для размещения … Словарь-справочник терминов нормативно-технической документации
безнапорное движение жидкости — безнапорный поток Движение жидкости со свободной поверхностью на всей длине потока. [СО 34.21.308 2005] Тематики гидротехника Синонимы безнапорный поток … Справочник технического переводчика
безнапорное движение жидкости. — 3.13.4 безнапорное движение жидкости. Безнапорный поток: Движение жидкости со свободной поверхностью на всей длине потока. Источник: СО 34.21.308 2005: Гидротехника. Основные понятия. Термины и определения … Словарь-справочник терминов нормативно-технической документации
ГОСТ 15528-86: Средства измерений расхода, объема или массы протекающих жидкости и газа. Термины и определения — Терминология ГОСТ 15528 86: Средства измерений расхода, объема или массы протекающих жидкости и газа. Термины и определения оригинал документа: 26. Акустический преобразователь расхода D. Akustischer Durch flußgeber E. Acoustic flow transducer F … Словарь-справочник терминов нормативно-технической документации
Гидравлический транспорт — (a. hydraulic transport, pipeline transport; н. Hydrotransport; ф. transport hydraulique; и. transporte hidraulico) технологический процесс перемещения материалов потоком воды. Использование воды как средства Г. т., а также для промывки… … Геологическая энциклопедия
Электроводонагреватель — электрический водонагреватель, устройство для нагрева воды за счёт энергии, получаемой из электросети, (тепловое действие тока) с целью последующего использования в технологических, хозяйственных, санитарно гигиенических или бытовых целях. Во… … Википедия
Что характеризует безнапорный поток
Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.
если угол в радианах, или
Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.
Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени
Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным
Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q1=Q2= const, откуда
Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).
Потерянная энергия или потерянный напор обозначаются 
Уравнение Бернулли для реальной жидкости будет иметь вид:
Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).
Потерянная высота 
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Выражение, стоящее перед 
Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.
Понятие о движении жидкости
В предыдущей статье было подробно рассмотрено ключевое понятие для гидравлики – давление. Теперь, во второй части этой статьи, я постараюсь максимально просто рассказать про движение жидкости.
Для начала рассмотрим, какое бывает движение жидкости. Существует большое количество различных классификаций и подходов к математическому описанию движения, но мы практически все это опустим, упомянем лишь, что в инженерной практике преимущественно рассматривается так называемое установившееся равномерное движение.
Это означает, что мы рассматриваем поток жидкости как замороженную картинку. Обычно системы водоснабжения и канализации рассчитывают именно так, принимая при этом пиковую нагрузку (расходы). Кроме того отметим, что рассматриваем далее движение реальной жидкости (т.е. в ней действуют силы внутреннего трения).
Это означает, что жидкость испытывает сопротивление своему движению, и тратит на движение свою энергию, которую называют напором жидкости.
Для нас также важно то, что движение жидкости может быть безнапорным и напорным.
Виды движения жидкости
Движение жидкости подчиняется двум основным уравнениям.
Уравнение неразрывности потока жидкости
Q – расход жидкости; объем жидкости, проходящий через живое сечение потока ω за единицу времени. В системе СИ измеряется в м 3 /с. Поскольку 1 кубометр – это очень много, то обычно эту единицу измерения используют для рек. В инженерной практике оперируют [л/с], величиной, в 1000 раз меньшей. Так, обычно, умываясь, из смесителя к нам в руки направляется 0,1 – 0,2 л/с воды.
v – средняя скорость потока жидкости в живом сечении. Дело в том, что если посмотреть на распределение скоростей частиц жидкости по сечению, например в напорном трубопроводе, то получится, что по центру скорость движения максимальна, а у стенок трубы равна 0. Т.е. скорости не одинаковы, поэтому используют понятие средней скорости. Измеряется в метрах в секунду (м/c). Скорость движения воды в системах водоснабжения и водоотведения примерно 0,7 — 1,5 м/с
Пример. Какой расход движется по трубе внутренним диаметром 40 мм в напорном режиме, если средняя скорость потока составляет 1,2 м/c?
Решение: площадь живого сечения трубы = площадь круга диаметром 40 мм. Площадь круга: ω = 3,14*d²/4 = 3,14*0,04²/4 = 0,00126 м². Тогда расход: Q = ω·v = 0,00126 · 1,2 = 0,00151 м³/с = 1,51 л/с.
Здесь представим сразу упрощенный вид уравнения Бернулли для напорного движения жидкости, который используют для расчета трубопроводных систем. В нем пренебрегают скоростными напорами (кинетической энергией жидкости в сечениях потока) ввиду малости этих скоростей для систем водоснабжения и водоотведения.
Уравнение Бернулли составляют для любых двух сечений одного потока жидкости. Оно связывает между собой скорости движения жидкости и давления в этих сечениях.
Уравнение Бернулли
Здесь: Z₁ – положение (отметка) сечения 1-1, выражается в метрах.
H₁ – напор в сечении 1-1 (избыточное давление в сечении 1-1, выраженное в метрах столба жидкости H₁ = p₁/ρg)
Z₂ – положение (отметка) сечения 2-2, выражается в метрах.
H₂ – напор в сечении 2-2 (избыточное давление в сечении 2-2), выражается также в метрах
hf – общая потеря напора при движении жидкости от сечения 1-1 до сечения 2-2. Происходит за счет работы сил трения в жидкости. При определенных условиях зависит от шероховатости
Пример. Какой напор будет в точке установки смесителя (точка 2) при величине напора воды в точке подключения в квартиру (точка 1) равном 5 м? Потерю напора при движении расчетного расхода по указанному пути принять 2 м. Точка 1 расположена на высоте 1 м от пола, точка 2 расположена на высоте 0,5 м от пола.
Решение: Отметки записываются относительно плоскости сравнения. Это может быть абсолютно любая горизонтальная плоскость. В данном случае удобно принять за плоскость сравнения поверхность пола.
1 + 5 = 0,5 + H₂ + 2, H₂ = 3,5м.
Отметим, что этот напор 3,5 м будет полностью потрачен в самом смесителе. В месте выхода воды из смесителя – атмосферное давление. Избыточное давление в этом месте равно 0 м.вод.ст.
Это выглядит довольно просто, однако сложность заключается в том, что в реальной жизни величину потери напора hf необходимо определять. Какие бывают потери напора, и как их определять – читайте третью статью в данном цикле
Напорное и безнапорное движение жидкости
По характеру движения жидкости потоки делят на напорные, безнапорные и
Напорный поток полностью ограничен со всех сторон твердыми стенками. Движение жидкости в таком потоке происходит под давлением (напорного резервуара или насоса). Примером может служить движение воды в водопроводе.
Безнапорный поток — это поток со свободной поверхностью, в которомром жидкость перемещается только под действием силы тяжести. Примером безнапорного потока может служить движение воды в реках, каналах.
Струи — это потоки, ограниченные со всех сторон жидкой или газообразной средой. В этом случае движение жидкости происходит по инерции под влиянием начальной скорости, созданной давлением или силой тяжести.
Расход и средняя скорость потока. Расход потока Q (м 3 /с) в данном сечении равен произведению площади живого сечения потока S на среднюю скорость в этом сечении Vcp:
Средняя скорость потока в данном сечении — воображаемая, фиктивная скорость потока, одинаковая для всех точек данного живого сечения, с которой через живое сечение проходил бы расход, равный фактическому. При неравномерном движении средняя скорость в различных живых сечениях по длине потока различна. При равномерном движении средняя скорость по типе потока постоянна во всех живых сечениях.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Безнапорное движение жидкости
11. Безнапорное движение жидкости
При безнапорном движении жидкости часть периметра живого сечения потока жидкости ограничивается газовой средой, давление в которой равно атмосферному давлению. Типов безнапорных потоков достаточно много, это и безнапорное движение жидкости в трубах, и потоки жидкости в открытых руслах, и т.д. Тем не менее, несмотря на разнообразие таких потоков, с точки зрения гидравлики их можно разделить на установившиеся потоки с равномерным движением жидкости и неустановившиеся потоки, часто называемые быстротоками. Наибольший интерес для нас играют потоки первой группы, с которыми чаще всего приходится встречаться специалистам горной промышленности. Быстротоки, как правило, являются предметом изучения для специальных дисциплин гидротехнического профиля. Поскольку установившиеся потоки жидкости, независимо от их вида совершенно одинаковы, то расчёты параметров таких потоков общие и могут быть продемонстрированы на простом примере.
11.1. Классификация безнапорных потоков
Прежде всего, следует отметить, что сколь-нибудь совершенной и законченной классификации безнапорных потоков отвечающей их многообразию не существует, попытаемся выделить некоторые типы потоков по их основным признакам.
На начальной стадии разделим все потоки по их происхождению на две группы: естественные (природные) и искусственные (созданные человеком). К потокам первой группы будут относиться все реки и другие природные русла, отличающиеся от рек чаще всего лишь по названию, а не по своей сути.
Безнапорные потоки также можно разделить на заглублённые и наземные. К категории заглублённых относятся все виды безнапорных трубопроводов. Среди безнапорных трубопроводов можно выделить трубопроводы из стальных, бетонных, асбоцементных и другого типа труб; по сечению безнапорные трубопроводы можно разделить на круглые,
некруглые и трубопроводы специального сечения.
Среди наземных безнапорных потоков можно вы 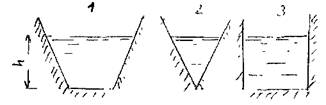
готовых элементов, когда водовод монтируется на трассе и обсаживаемые. При сооружении последних, как правило, предварительно сооружается земляное русло бедующего водовода (траншея, канава и др.), после чего такое русло обсаживается водоизоляционным материалом во избежание потерь при инфильтрации жидкости в почву. Наиболее часто встечающимися формами сечения таких водоводов являются водоводы трапециевидного (1), треугольного (2) и, реже всего, прямоугольного форм сечения (3).
Подавляющее число наземных потоков являются открытыми, т.е. сообщаются с атмосферой, однако, в тех случаях, когда необходимо предотвратить потери транспортируемой жидкости от испарения (в странах с жарким климатом), водоводы перекрывают. В ряде случаев водоводы монтируются над поверхностью земли на специальных опорах и мостовых переходах, создавая тем самым акведуки.
И, наконец, можно разделить безнапорные потоки на постоянно действующие и работающие в сезонном режиме.
11.2. Основные методы гидравлического расчёта безнапорных потоков Равномерное движение жидкости в безнапорном потоке поддерживается за счёт разницы в уровне свободной поверхности между начальным и конечным живыми сечениями потока. Чтобы движение жидкости в потоке было равномерным, должны быть выполнены следующие необходимые условия:
живые сечения потока вдоль всего русла должны быть одинаковыми как по размеру, так и по форме,
уровень свободной поверхности жидкости должен быть параллелен профилю дна русла,
шероховатость стенок русла должна быть одинакова по всей длине русла. При выполнении этих условий гидравлический расчёт сводится в основном к определению расхода в потоке жидкости, а также некоторых параметров потока.
Поскольку по условиям равномерности потока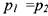
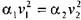
Бернулли примет вид:
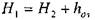
где:
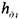
Величина скоростного коэффициента Шези С определяется по экспериментальной формуле Маннинга:
где: