Что характеризует модуль ускорения

Формулы модуля ускорения для прямолинейного и криволинейного движения. Пример решения задачи

В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.

Что такое ускорение?

Вам будет интересно: Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления

Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.

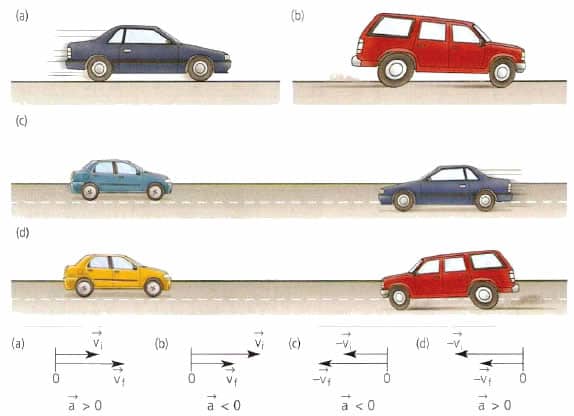
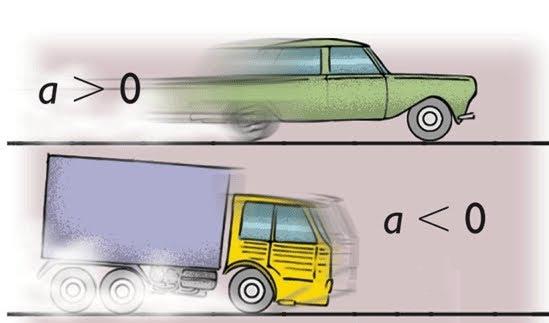
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:

Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).

Полное ускорение и его компоненты при движении тела по кривой

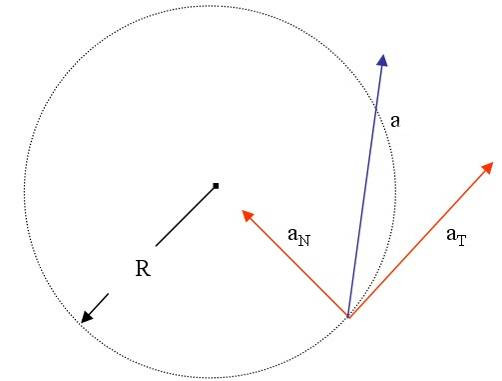
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.

Угловое ускорение

Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:

Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.

Пример решения задачи

Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:

at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).

Нормальная компонента вычисляется так:

an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.

Теперь можно рассчитать полное ускорение. Оно будет равно:

a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

α = at/r = 76/0,2 = 380 рад/с2.

Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.

Источник

Нормальное и тангенциальное ускорение

Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.

Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.

Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.

В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением . Тангенциальное ускорение описывает степень изменения скорости по модулю:

Нормальное ускорение – это составляющая ускорения, которая направлена к центру кривизны траектории, то есть она является нормалью (направлена перпендикулярно) к скорости. Нормальное ускорение описывает степень изменения скорости по направлению:

Здесь R – это радиус кривизны траектории в заданной точке.

Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:

.

Источник

Кинематика. Ускорение.

Ускорение – величина, характеризующая быстроту изменения скорости. Движение, как правило, неравномерно, т. е. непрерывно изменяется от одного момента времени к другому. Например, автобус, трогаясь с места, со временем набирает скорость, а приближаясь к остановке он замедляет свое движение. Для вычисления скорости в любой момент времени нужно знать, как она изменяется в единицу времени.

Рассмотрим такое неравномерное движение тела, при котором его скорость за любые равные промежутки времени будет изменяться одинаково. Такое движение называется равноускоренным.

Ускорением тела при его равноускоренном движении называют физическую величину, равную пределу отношения изменения скорости к промежутку времени, в течение которого это изменение произошло:

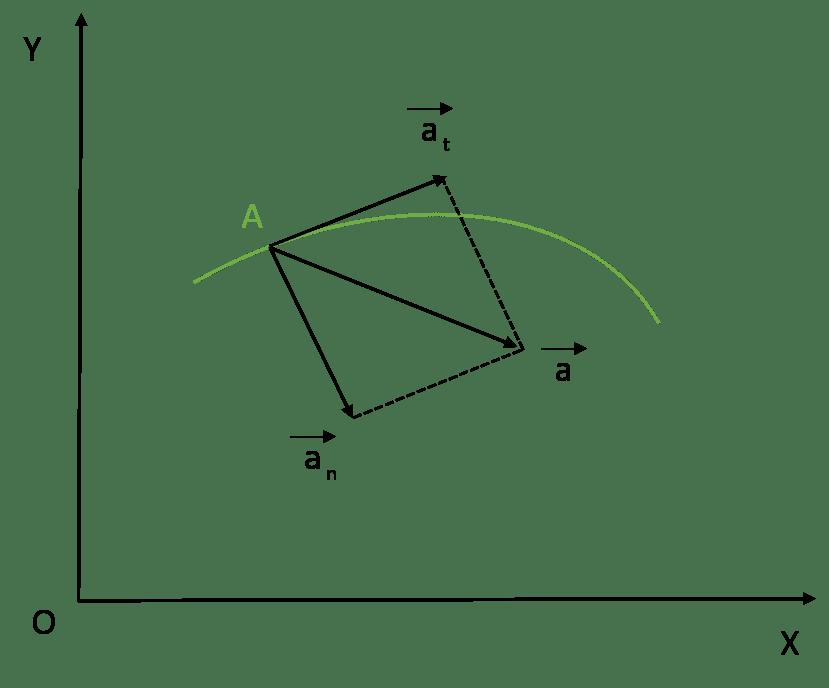
Ускорение, как представлено на рисунке, направлено в сторону вогнутости траектории. Его можно разложить на две составляющие: тангенциальную – по касательной к траектории движения, и нормальную – перпендикулярно траектории.

Следуя из этого, проекцию ускорения a_τ на касательную к траектории называют касательным (тангенциальным) ускорением, а проекцию a_n на нормаль – нормальным (центростремительным) ускорением.

Касательное (тангенциальное) ускорение характеризует изменение скорости по модулю при криволинейном движении:

Нормальное ускорение характеризует изменение скорости по направлению и определяется формулой:

где R – радиус кривизны траектории в соответствующей ее точке.

При криволинейном движении полное ускорение складывается из тангенциального и нормального ускорений и определяется по формулой:

Источник