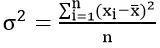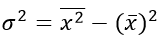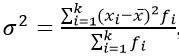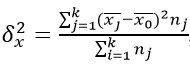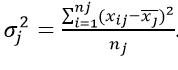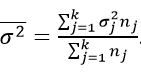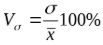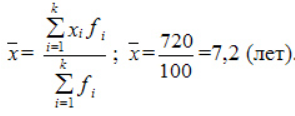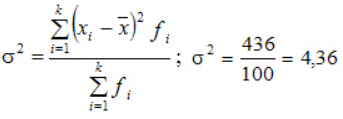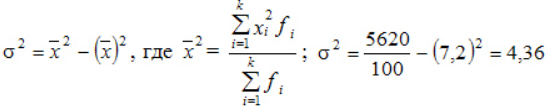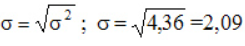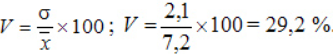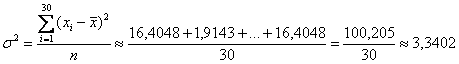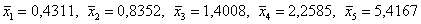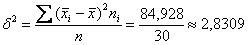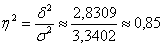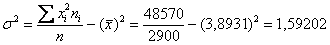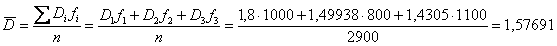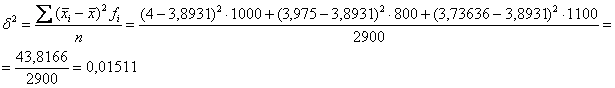Что характеризует общая дисперсия

Что характеризует общая дисперсия

5.3 чЙДЩ ДЙУРЕТУЙК Й РТБЧЙМП ЙИ УМПЦЕОЙС

йОПЗДБ ВЩЧБЕФ ОЕПВИПДЙНП РТПУМЕДЙФШ ЛПМЙЮЕУФЧЕООЩЕ ЙЪНЕОЕОЙС РТЙЪОБЛБ РП ЗТХРРБН, ОБ ЛПФПТЩЕ ТБЪДЕМСЕФУС УПЧПЛХРОПУФШ, Б ФБЛЦЕ Й НЕЦДХ ЗТХРРБНЙ. фБЛПЕ ЙЪХЮЕОЙЕ ЧБТЙБГЙЙ ДПУФЙЗБЕФУС ЧЩЮЙУМЕОЙЕН Й БОБМЙЪПН ТБЪМЙЮОЩИ ЧЙДПЧ ДЙУРЕТУЙЙ.

чЩДЕМСАФ ДЙУРЕТУЙА ПВЭХА, НЕЦЗТХРРПЧХА Й ЧОХФТЙЗТХРРПЧХА.

пВЭБС ДЙУРЕТУЙС ЙЪНЕТСЕФ ЧБТЙБГЙА РТЙЪОБЛБ ЧП ЧУЕК УПЧПЛХРОПУФЙ РПД ЧМЙСОЙЕН ЧУЕИ ЖБЛФПТПЧ, ПВХУМПЧЙЧЫЙИ ЬФХ ЧБТЙБГЙА

.

(5.5)

нЕЦЗТХРРПЧБС ДЙУРЕТУЙС ИБТБЛФЕТЙЪХЕФ УЙУФЕНБФЙЮЕУЛХА ЧБТЙБГЙА, Ф.Е. ТБЪМЙЮЙС Ч ЧЕМЙЮЙОЕ ЙЪХЮБЕНПЗП РТЙЪОБЛБ, ЧПЪОЙЛБАЭЙЕ РПД ЧМЙСОЙЕН РТЙЪОБЛБ-ЖБЛФПТБ, РПМПЦЕООПЗП Ч ПУОПЧБОЙЕ ЗТХРРЙТПЧЛЙ

,

(5.11)

чОХФТЙЗТХРРПЧБС ПФТБЦБЕФ УМХЮБКОХА ЧБТЙБГЙА, Ф.Е. ЮБУФШ ЧБТЙБГЙЙ, РТПЙУИПДСЭХА РПД ЧМЙСОЙЕН ОЕХЮФЕООЩИ ЖБЛФПТПЧ Й ОЕ ЪБЧЙУСЭХА ПФ РТЙЪОБЛБ-ЖБЛФПТБ

.

(5.12)

уТЕДОСС ЙЪ ЧОХФТЙЗТХРРПЧЩИ

.

(5.13)

уХЭЕУФЧХЕФ ЪБЛПО, УЧСЪЩЧБАЭЙК ФТЙ ЧЙДБ ДЙУРЕТУЙЙ. пВЭБС ДЙУРЕТУЙС ТБЧОБ УХННЕ ЙЪ ЧОХФТЙЗТХРРПЧЩИ Й НЕЦЗТХРРПЧЩИ ДЙУРЕТУЙК

.

(5.14)

дБООПЕ УППФОПЫЕОЙЕ ОБЪЩЧБАФ РТБЧЙМПН УМПЦЕОЙС ДЙУРЕТУЙЙ. ьФП РТБЧЙМП РТЙНЕОСЕФУС РТЙ ЙУЮЙУМЕОЙЙ РПЛБЪБФЕМЕК ФЕУОПФЩ УЧСЪЙ, Ч ДЙУРЕТУЙПООПН БОБМЙЪЕ.

ч УФБФЙУФЙЮЕУЛПН БОБМЙЪЕ ЫЙТПЛП ЙУРПМШЪХЕФУС РПЛБЪБФЕМШ, РТЕДУФБЧМСАЭЙК УПВПК ДПМА НЕЦЗТХРРПЧПК ДЙУРЕТУЙЙ Ч ПВЭЕК ДЙУРЕТУЙЙ. пО ОПУЙФ ОБЪЧБОЙЕ ЬНРЙТЙЮЕУЛПЗП ЛПЬЖЖЙГЙЕОФБ ДЕФЕТНЙОБГЙЙ №104; 2

.

(5.15)

пО РПЛБЪЩЧБЕФ ДПМА ПВЭЕК ЧБТЙБГЙЙ, ПВХУМПЧМЕООХА ЧБТЙБГЙЕК ЗТХРРЙТПЧПЮОПЗП РТЙЪОБЛБ.

лПТЕОШ ЛЧБДТБФОЩК ЙЪ ЬНРЙТЙЮЕУЛПЗП ЛПЬЖЖЙГЙЕОФБ ДЕФЕТНЙОБГЙЙ РТЕДУФБЧМСЕФ УПВПК ЬНРЙТЙЮЕУЛПЕ ЛПТТЕМСГЙПООПЕ ПФОПЫЕОЙЕ №104;

.

(5.16)

дБООЩК РПЛБЪБФЕМШ НПЦЕФ РТЙОЙНБФШ ЪОБЮЕОЙС Ч РТЕДЕМБИ ПФ 0 ДП 1, ЕУМЙ №104; =0, ФП УЧСЪШ НЕЦДХ ТЕЪХМШФБФЙЧОЩН Й ЗТХРРЙТПЧПЮОЩН РТЙЪОБЛПН ПФУХФУФЧХЕФ, ЕУМЙ №104; =1, ФП УЧСЪШ ЖХОЛГЙПОБМШОБС.

йНЕАФУС ДБООЩЕ П РТПЙЪЧПДЙФЕМШОПУФЙ ФТХДБ РП ДЧХН ЗТХРРБН ТБВПЮЙИ

1
4
4
0
1

1 ЗТХРРБ				2 ЗТХРРБ
йНЕАЭЙЕ УРЕГЙБМШОХА РПДЗПФПЧЛХ				оЕ ЙНЕАЭЙЕ УРЕГЙБМШОХА РПДЗПФПЧЛХ
оПНЕТ ТБВПЮЕЗП	рТПЙЪЧПДЙФЕМШОПУФШ ФТХДБ Ф.ТХВ/ЮЕМ.			оПНЕТ ТБВПЮЕЗП	рТПЙЪЧПДЙФЕМШОПУФШ ФТХДБ Ф.ТХВ/ЮЕМ.
ЙФПЗП	110	26	йФПЗП	75	10

пРТЕДЕМЙФШ ЗТХРРПЧЩЕ ДЙУРЕТУЙЙ, УТЕДОАА ЙЪ ЗТХРРПЧЩИ ДЙУРЕТУЙК, НЕЦЗТХРРПЧХА ДЙУРЕТУЙА, ПВЭХА ДЙУРЕТУЙА, ЛПЬЖЖЙГЙЕОФ ДЕФЕТНЙОБГЙЙ Й ЬНРЙТЙЮЕУЛПЕ ЛПТТЕМСГЙПООПЕ ПФОПЫЕОЙЕ.

1. дМС ТБУЮЕФБ ЗТХРРПЧЩИ ДЙУРЕТУЙК ЙУЮЙУМЙН УТЕДОЙЕ РП ЛБЦДПК ЗТХРРЕ

тБУЮЕФ ДЙУРЕТУЙК РП ЗТХРРБН (ЖПТНХМБ 5.4):

2. тБУУЮЙФБЕН УТЕДОАА ДЙУРЕТУЙА ЙЪ ЗТХРРПЧЩИ (ЖПТНХМБ 5.13)

3. йУЮЙУМЙН НЕЦЗТХРРПЧХА ДЙУРЕТУЙА. дМС ЬФПЗП РТЕДЧБТЙФЕМШОП ПРТЕДЕМЙН ПВЭХА УТЕДОАА РП РТПЙЪЧПДЙФЕМШОПУФЙ ФТХДБ

ъБФЕН ТБУУЮЙФЩЧБЕН НЕЦЗТХРРПЧХА ДЙУРЕТУЙА (ЖПТНХМБ 5.11):

4. йУЮЙУМЙН ПВЭХА ДЙУРЕТУЙА РП РТБЧЙМХ УМПЦЕОЙС ДЙУРЕТУЙК (ЖПТНХМБ 5.14):

5. пРТЕДЕМСЕН ЛПЬЖЖЙГЙЕОФ ДЕФЕТНЙОБГЙЙ РП ЖПТНХМЕ 5.15

6. ьНРЙТЙЮЕУЛПЕ ЛПТТЕМСГЙПООПЕ ПФОПЫЕОЙЕ ТБУУЮЙФЩЧБЕН РП ЖПТНХМЕ 5.16

оБТСДХ У ЙЪХЮЕОЙЕН ЧБТЙБГЙЙ ЛПМЙЮЕУФЧЕООЩИ РТЙЪОБЛПЧ НПЦЕФ ТБУУНБФТЙЧБФШУС ДЙУРЕТУЙС БМШФЕТОБФЙЧОЩИ РТЙЪОБЛПЧ.

.

(5.17)

ъОБС УТЕДОЕЕ ЪОБЮЕОЙЕ БМШФЕТОБФЙЧОПЗП РТЙЪОБЛБ ПРТЕДЕМСЕН ДЙУРЕТУЙА РП ЖПТНХМЕ :

.

(5.18)

рТЕДЕМШОПЕ ЪОБЮЕОЙЕ ДЙУРЕТУЙЙ БМШФЕТОБФЙЧОПЗП РТЙЪОБЛБ ТБЧОП 0.25 РТЙ p =0.5

=pq=p(1-p)=0.5(1-0.5)=0.5ћ0.5=0.25

уТЕДОЕЕ ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ ТБЧОП

,

(5.19)

чБТЙБГЙС БМШФЕТОБФЙЧОПЗП РТЙЪОБЛБ ЙУРПМШЪХЕФУС Ч УПГЙПМПЗЙЮЕУЛЙИ ПВУМЕДПЧБОЙСИ, РТПЧЕДЕОЙЙ ЧЩВПТПЮОПЗП ОБВМАДЕОЙС Й Ф.Д.

ч ЗТХРРЕ УФХДЕОФПЧ У ЮЙУМЕООПУФША 30 ЮЕМПЧЕЛ ВЩМБ РТПЧЕДЕОБ ЛПОФТПМШОБС ТБВПФБ ТЕЪХМШФБФЩ ЛПФПТПК РПЛБЪБМЙ, ЮФП 7 ЮЕМПЧЕЛ ОЕ УРТБЧЙМЙУШ У ЪБДБОЙЕН. пРТЕДЕМЙФШ ДЙУРЕТУЙА Й УТЕДОЕЕ ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ БМШФЕТОБФЙЧОПЗП РТЙЪОБЛБ.

уФХДЕОФЩ УРТБЧЙЧЫЙЕУС У ЪБДБОЙЕН ПРТЕДЕМСАФУС ЛБЛ (30-7)=23 ЮЕМПЧЕЛБ, ЙИ ДПМС УПУФБЧЙФ . оБИПДЙН УФХДЕОФПЧ ОЕ УРТБЧЙЧЫЙИУС У ЪБДБОЙЕН «q» q=(1-p)=(1-0.76)=0.24.

пРТЕДЕМСЕН ДЙУРЕТУЙА РП ЖПТНХМЕ 5.18

пРТЕДЕМСЕН УТЕДОЕЕ ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ РП ЖПТНХМЕ 5.19

Источник

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где x_i – значение из ряда;

f_i – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».

Как найти данную дисперсию? По формуле:

где k – количество групп;

n_j – элементов в группе с индексом j.

Внутригрупповая дисперсия

Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

Пример расчета дисперсии

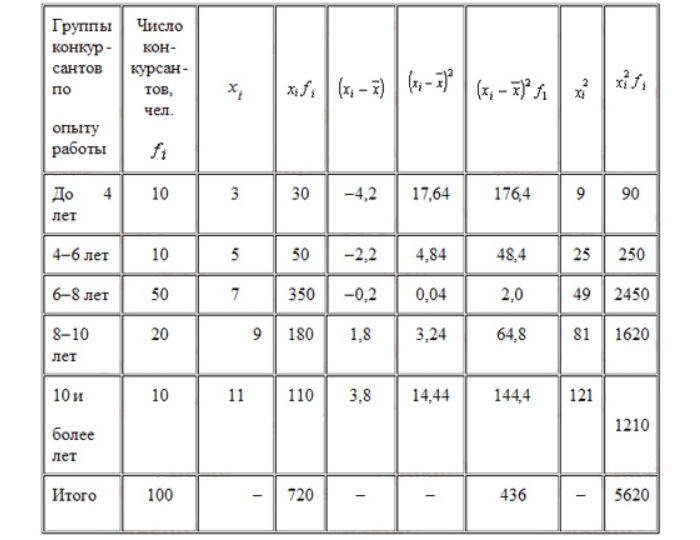
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Источник

15. Общая, групповые, внутригрупповая и межгрупповая дисперсия.
Правило сложения дисперсий

…из соображений гуманности сразу весь список 🙂 Тема не самая простая, а точнее, кропотливая, но я научу вас БЫСТРО находить все перечисленные дисперсии, а также расскажу, что они означают и для чего нужны. Для освоения данного урока нужно понимать, что такое дисперсия и группировка данных (предыдущая статья) и уметь выполнять несложные расчёты. Впрочем, всё кратко повторим по ходу пьесы, и я немедленно начинаю разбирать материал:

По данным Примера 55 рассчитать общую, групповые, внутригрупповую и межгрупповую дисперсию

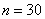
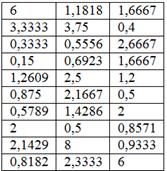
Напоминаю, что в той задаче нам были даны относительные показатели металлоёмкости станков (т/кВт):

и по исходным данным мы сразу вычислили общую среднюю:
т/кВт

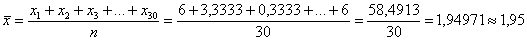
Общая дисперсия – показатель не новый, и её мы уже неоднократно рассчитывали ранее. Для этого нужно найти квадраты отклонений вариант от общей средней: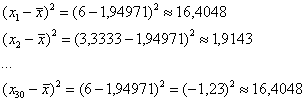

вычислить их сумму и разделить её на объём совокупности:

Вычисления удобно проводить в Экселе, и чуть позже будет ролик по этой теме, буквально минут за 5 разгромим всю задачу.

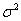
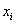
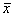
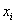
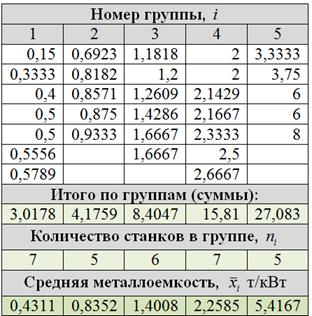
Общая дисперсия характеризует меру рассеяния значений относительно общей средней . Чем дисперсия больше, тем дальше разбросаны от средней, и наоборот, чем дисперсия меньше, тем они к средней ближе.

Теперь вычислим групповые дисперсии. Для этого, очевидно, нужно разбить совокупность на группы, при этом группировку можно выполнить разными способами. В Примере 55 мы упорядочили варианты 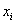по возрастанию и провели удачную равнонаполненную группировку:

В результате получилось 5 групп объёмом 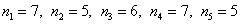, по которым мы рассчитали групповые средние:

И как вы правильно догадались, у нас будет 5 групповых дисперсий. По каждой группе своя. Для этого нужно рассчитать квадраты отклонений 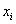от СВОИХ групповых средних:

Тушеваться не надо, в Экселе мы эти вычисления выполним в несколько щелчков, и если вам не терпится посмотреть, как это происходит, то можно сразу перейти к видеоролику (см. ниже).

Таким образом, групповые дисперсии:

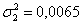
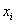
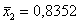
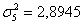
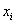
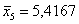
Групповая дисперсия характеризует меру разброса значений группы относительно групповой средней. В нашем примере наименьшей получилась дисперсия по 2-й группе: , это означает, что варианты этой группы расположены достаточно близко к . Максимальная дисперсия – в 5-й группе: , это означает, что многие варианты этой группы расположены достаточно далеко от .

внутригрупповая дисперсия – это средняя, а точнее средневзвешенная арифметическая групповых дисперсий:

И внимательный читатель заметил, что для нахождения внутригрупповой дисперсии не обязательно рассчитывать групповые дисперсии, ибо:
,
т.е. достаточно просуммировать числа нижней строки вышеприведённой таблицы.

Внутригрупповая дисперсия характеризует среднюю (средневзвешенную) вариацию значений 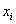по группам. Должен сказать, что название «внутригрупповая» не совсем удачное и часто вызывает путаницу, в немалом количестве источников под ним понимают групповую дисперсию, и это тоже вполне себе логично. И посему точнее звучит «средняя из групповых».

И, наконец, ещё одна дисперсия 🙂

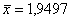
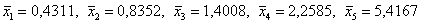
Рассмотрим общую среднюю и групповые средние .

Межгрупповая дисперсия – это дисперсия групповых средних относительно общей средней: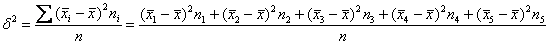

Для компактности удобно оформить небольшую расчётную табличку:

Таким образом:

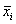
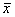
Межгрупповая дисперсия характеризует меру разброса групповых средних относительно общей средней. Чем эта дисперсия больше, тем дальше расположены групповые средние (многие из них) относительно общей средней .

Для общей, внутригрупповой и межгрупповой дисперсий справедливо так называемое правило сложение дисперсий:

, то есть общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсии.

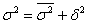
Примечание: в различных источниках встречаются разные обозначения этих дисперсий, и, кроме того, слагаемые правой части могут быть переставлены.

Проверим, всё ли мы правильно подсчитали: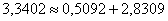

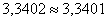
– получено верное равенство с точностью до погрешности округлений, таким образом, все дисперсии найдены верно.

Следует отметить, что правило сложения дисперсий справедливо не только для выборочной совокупности (как в нашем примере), но и для совокупности генеральной. Это не важно. Однако здесь нужно помнить, что выборочные дисперсии являются смещёнными оценками соответствующих генеральных дисперсий, и выборочные дисперсии можно исправить. После поправки правило сложения дисперсий, естественно, останется справедливым.

Ну а теперь смотрим видео о том, как быстро расправиться со всем этим безобразием:

Как вычислить дисперсии? (Ютуб)

И после изучения технической стороны вопроса вникнем в СМЫСЛ этих дисперсий.

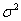
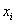
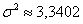
Как отмечалось выше, общая дисперсия характеризует меру вариации всей совокупности. И здесь есть такой элементарный вопрос: а почему варианты вообще разные, почему значения варьируются? Очевидно, они варьируются под действием ряда ФАКТОРОВ (как неслучайных, так и случайных). Таким образом, общая дисперсия учитывает все причины (факторы), которые обуславливают вариацию. Так в примере со станками разная металлоёмкость обусловлена различными типами станков, разными «поколениями» оборудования, разными условиями эксплуатации и, скорее всего, и другими причинами. И общая дисперсия учитывает ВСЕ эти факторы.

Теперь смотрим на правило сложения дисперсий: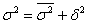
, то есть, общая дисперсия включает в себя внутригрупповую и межгрупповую дисперсию.

Межгрупповая дисперсия характеризует вариацию, обусловленную фактором, который лёг в основу группировки.

Внутригрупповая дисперсия отражает вариацию, обусловленную другими факторами.

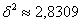
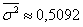
И даже если мы сгруппировали данные формально (как в нашем примере), то в основе группировки всё равно лежит некоторый группировочный фактор. Ибо числа-то в группах разные и тому есть причина! Условно предположим, что станки разбиты на 5 групп по их «поколениям» – от новейших до «древнейших». Тогда межгрупповая дисперсия отражает вариацию, обусловленную этим фактором (тем фактом, что станки принадлежат разным «поколениям»). А внутригрупповая дисперсия объясняется другими факторами.

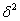
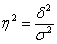
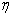
Возникает вопрос: как оценить СУЩЕСТВЕННОСТЬ ВЛИЯНИЯ фактора, который лёг в основу группировки? Ответ очевиден: чем больше межгрупповая дисперсия , тем сильнее влияние группировочного фактора. И для оценки существенности влияния рассчитывают эмпирический коэффициент детерминации (причинности), равный отношению межгрупповой дисперсии к дисперсии общей:
( – греческая буква «эта»)

Этот коэффициент характеризует долю вариации, объяснённую группировочным фактором.

В нашей задаче:

Таким образом, 85% вариации металлоёмкости объясняется тем фактом, что станки принадлежат разным «поколения», и оставшаяся часть вариации (15%) объясняется другими причинами.

Следует отметить, что это всего лишь одна из математических моделей. В том смысле, что мы можем рассмотреть другой группировочный фактор, провести новую группировку, подсчитать дисперсии и, возможно, тоже получить высокий коэффициент детерминации. И в этом не будет противоречия, ибо второй фактор по своей сути или через «перекрёстную взаимосвязь» может «накладываться» на фактор первой модели.

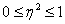
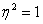
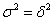
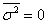
Эмпирический коэффициент детерминации изменяется в пределах , и чем он ближе к единице, тем сильнее влияние группировочного фактора на вариацию статистической совокупности. Если , то речь идёт о строгой функциональной зависимости, в этом случае , то есть внутригрупповая дисперсия (по правилу сложения) равна нулю: , и это в свою очередь означает, что в каждой группе находятся одинаковые и строго определённые значения (т.е. вариация по группам отсутствует).

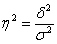
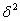
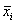
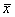
Наоборот, чем ближе к нулю, тем влияние группировочного фактора меньше; математически это означает, что межгрупповая дисперсия слишком малА, а это в свою очередь значит, что групповые средние расположены очень близко к общей средней . И логика здесь простА: если мы провели группировку и получили примерно одинаковые средние по группам, то влияние фактора явно слабО. Но это ещё не значит, что сам фактор не важный 😉

Об этом и других коэффициентах мы ещё поговорим, даже отдельный урок можно организовать, а пока вернёмся к нашим дисперсиям. Как вы знаете, дисперсию можно вычислить по определению или по формуле, и поэтому в разных задачах вы можете встретить разные формулы. Кроме того, вам могут быть предложены различные вариационные ряды, например, ряды не просто с «одиночными» вариантами, но ещё и с частотами по каждой группе:

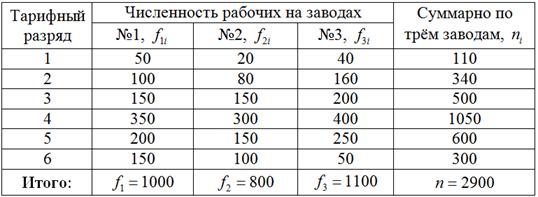
Распределение рабочих трех заводов одного объединения по тарифным разрядам характеризуется следующими данными:

Определить:
а) общую дисперсию;
б) дисперсию по каждому заводу (групповые дисперсии);
в) среднюю из групповых дисперсий (внутригрупповую дисперсию);
г) межгрупповую дисперсию;
д) проверить правило сложения дисперсий
е) вычислить эмпирический коэффициент детерминации и сделать вывод о том, насколько значимо различается квалификация рабочих на заводах. Иными словами, нужно выяснить, нанимали ли на какие-то заводы более квалицированных рабочих, чем на другие, или же квалификация по заводам примерно одинакова?

Для интереса засёк время – все вычисления у меня заняли чуть меньше трёх минут! И это в такой-то «страшной» задаче. А эта «страшная» задача, к слову, была предложена заочникам; очников «кошмарят» гораздо хуже. Там и групп может быть с десяток и чисел больше, 100-200. В относительно «лёгких случаях» групп обычно не более пяти.

Следует отметить, что разобранные дисперсии используются и в других задачах математической статистики, где их нужно рассчитывать немного с другой спецификой. И эти задачи уже на подходе 😉 На следующем уроке мы познакомимся с аналитической группировкой и гармонично разовьём тему с дисперсиями. Надеюсь, они вам понравились 🙂

Пример 60. Решение: а) Заполним расчётную таблицу: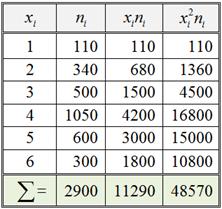

Вычислим общую среднюю: 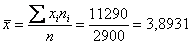(значение вычислено примерно, но далее для простоты я буду ставить знаки «равно»).
Вычислим общую дисперсию:

б) Заполним расчётную таблицу для каждой группы: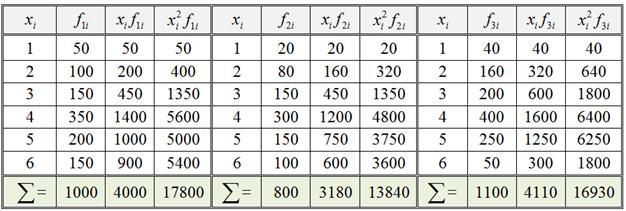

Найдем средние значения тарифного разряда по заводам (групповые средние):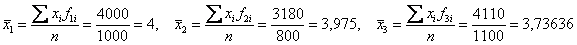

Вычислим групповые дисперсии: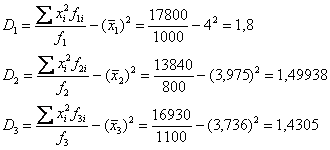
;

в) Вычислим среднюю из групповых (внутригрупповую) дисперсию:

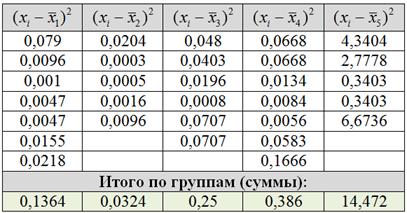
г) Для нахождения межгрупповой дисперсии удобно заполнить расчётную табличку: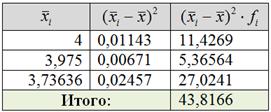

или расписать так:

д) Проверим правило сложения дисперсий:
(см. пункт «а»), что и требовалось проверить

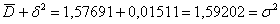
е) Вычислим эмпирический коэффициент детерминации: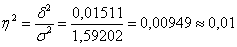
, примерно ноль.

Таким образом, средняя квалификация рабочих по заводам практически одинакова (иными словами, фактор, положенный в основу группировки (распределение рабочих по заводам) не оказывает никакого влияния – нельзя сказать, что на какой-то завод специально нанимали более квалифицированных рабочих).

! Примечание: но группировочный фактор сам по себе важен, поскольку распределяет рабочих по заводам. Только вот на тарифные разряды это практически не влияет.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник