что относится к многогранникам

Что такое многогранник? Примеры

Примеры многогранников:

1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);

Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.

Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.

Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.

Популярное

Геометрическая форма коробочки издалека напоминает округлую форму, что делает акцент на сходство с мячиком. Но если присмотреться по внимательнее, то мы видим.

Достаточно часто возникает вопрос о практическом применении бумажных развёрток. Какой смысл в бумажном моделировании?

Памятник многограннику «Усечённый большой додекаэдр» был обнаружен в городе Обнинск, напротив здания «ДОСААФ» (ул.Шацкого, д.14).

У каждого из пяти тел Платона можно определить следующие математические характеристики: 1. Радиус сферы описанной вокруг многогранника; 2. Радиус сферы.

Для Вашего удобства мы снизили стоимость доставки наборов «Волшебные грани» в разы!

Источник

Что относится к многогранникам

Кратко охарактеризуем геометрические свойства некоторых многогранников:

а) модель		б) эпюр
Рисунок 67. Пирамида

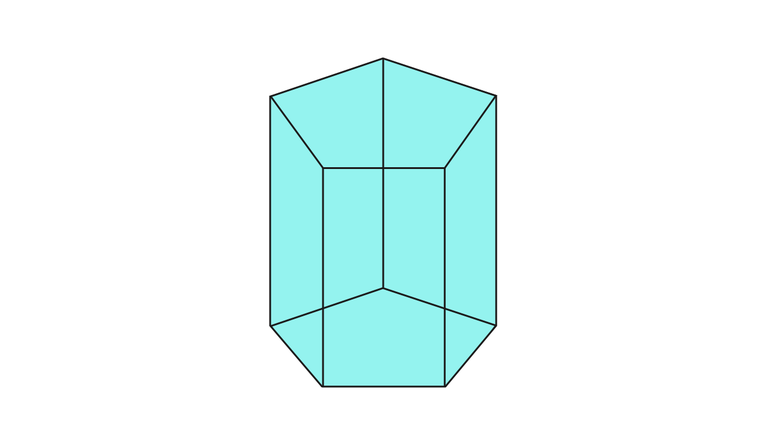
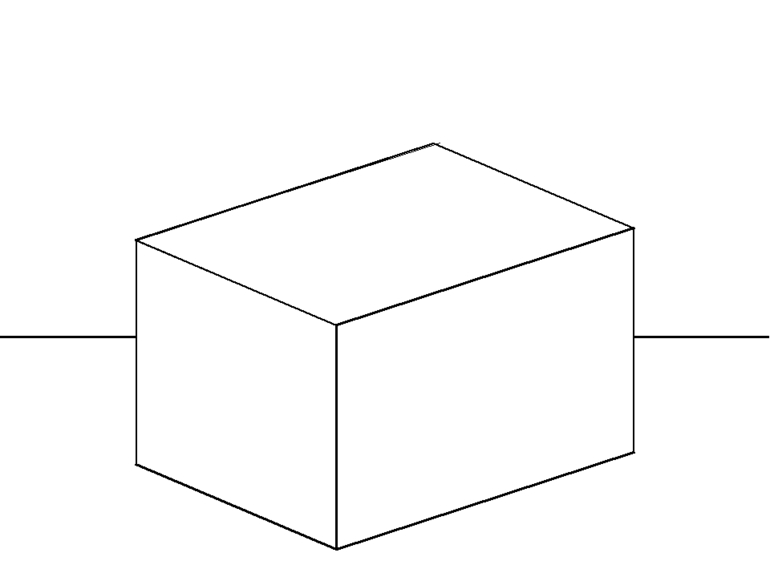
2. Призма — многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68).

а) модель		б) эпюр
Рисунок 68. Призма

3. Призматоид — многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований (рис.69).

а) модель		б) эпюр
Рисунок 69. Призматоид

4. Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными . Углы при вершинах такого многогранника равны между собой.

Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

а) модель		б) эпюр
Рисунок 70. Тетраэдр

Гексаэдр — правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов.

а) модель		б) эпюр
Рисунок 71. Гексаэдр

Октаэдр — правильный восьмигранник ( рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

а) модель		б) эпюр
Рисунок 72. Октаэдр

Додекаэдр — правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 73).

а) модель		б) эпюр
Рисунок 73. Додекаэдр

Икосаэдр — состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины (рис.74).

а) модель		б) эпюр
Рисунок 74. Икосаэдр

5. Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Источник

Основные понятия

Определение многогранника включает в себя такое понятие, как геометрическое тело, созданное из плоских многоугольников. Их число конечное. От формы каждого из них напрямую зависят свойства итоговой фигуры. Их делят на 2 типа:

Поскольку многогранники рассматриваются в трехмерном евклидовом пространстве, они относятся к стереометрии. А их многоугольники лежат в двумерной плоскости, что относится к планиметрии. Поэтому основные свойства и понятия формируются, включая в себя обе эти науки.

Параметры фигуры

Правильные многогранники

Правильные многогранники — фигуры, грани которых представляют собой многоугольники с равными углами и сторонами. Также они называются Платоновыми телами. Всего существует 5 соответствующих тел, подробные характеристики которых представлены в таблице.

Правильные многогранники изучались древними греками. Однако первые модели в орнаменте и по отдельности появились намного раньше. Например, археологами были найдены вырезанные каменные шары в Шотландии, которые датируются поздним неолитом (соответственно, за 1000 лет до жизни и деятельности Платона).

Призма и ее особенности

Геометрическое тело называют прямым, если каждое ребро лежит перпендикулярно основанию. Также они становятся высотами. Когда грани идентичны, многоугольник считается правильным, и его диагональное сечение образует параллелограмм.

Характеристики параллелепипеда

Параллелепипед — многогранник, основанием и гранями которого является параллелограмм. Фигура характеризуется как неправильная. Основные характеристики:

Когда все грани параллелограмма являются прямоугольными, фигура характеризуется, как прямоугольная. Длина каждого ребра считается линейным размером. У такой фигуры есть три измерения. При этом справедлива формула d² = a² + b² + c². При расчетах руководствуются и другими. Для объема : V = abc, для площади многогранника: S=2·(ab+ bc +ac).

Пирамида и ее величины

Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:

Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.

Источник

Лекция по математике на тему «Многогранники»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Понятие многогранника. Виды многогранников.

Выпуклые и невыпуклые, правильные и неправильные

Преподаватель: Горячева А.О.

Многогранником называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников.

Выпуклые и невыпуклые многогранники.

Правильные (Платоновы тела) и неправильные многогранники.

Если данное утверждение не выполняется, многогранник будет являться невыпуклым (рис. 2б).

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук» (Л.Кэрролл).

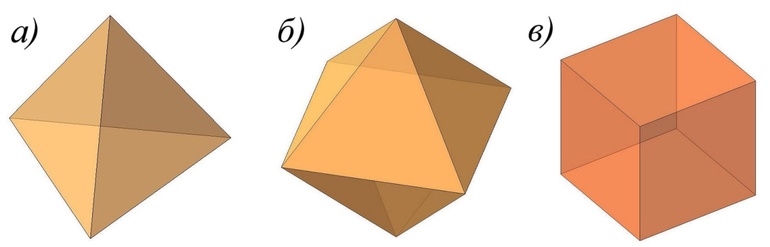
Всего существует пять правильных многогранников (рис. 3).

Если посчитать количество граней, ребер и вершин указанных многогранников, получим (таб. 1):

Тип правильного многогранника

Число сторон у грани

Число рёбер, примыкающих к вершине

Общее число вершин

Общее число граней

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создавались философские школы. Большое значение в этих школах приобрели рассуждения, с помощью которых удалось получить новые геометрические свойства.

Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел: Вселенная – додекаэдр, Земля – куб, Огонь – тетраэдр, Вода – икосаэдр,

Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно, и с разным числом сторон) и все многогранные углы равны.

Существует тринадцать полуправильных многогранников, которые носят название Архимедовых тел: усеченный тетраэдр (рис. 4а), усеченный октаэдр (рис. 4б), усеченный икосаэдр (рис. 4в), усеченный куб (рис. 4г), усеченный додекаэдр (рис. 4д), кубооктаэдр (рис. 4е), икосододекаэдр (рис. 4ж), усеченный кубооктаэдр (рис. 4з), усеченный икосододекаэдр (рис. 4и), ромбокубооктаэдр (рис. 4к), ромбоикосододекаэдр (рис. 4л), плосконосый куб (рис. 4м), плосконосый додекаэдр (рис. 4н), призма (рис. 4о) и антипризма (рис. 4п). Антипризма – это многогранник, у которого две параллельные грани (основания) — равные между собой правильные n-угольники, а остальные 2n граней (боковые грани) — правильные треугольники.

Тетраэдр и гексаэдр (куб) не имеют звёздчатых форм, так как их грани при продлении через рёбра более не пересекаются.

Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр (рис. 5а), большой додекаэдр (рис. 5б), большой звёздчатый додекаэдр (рис. 5в). Первые две из них были открыты И. Кеплером в 1619 году, а третью почти 200 лет спустя построил французский математик и механик Л. Пуансо (1809г). Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо.

Икосаэдр имеет 59 звёздчатых форм. Одна из этих звёздчатых форм, называемая большим икосаэдром (рис. 6), является одним из четырёх правильных звёздчатых многогранников Кеплера—Пуансо. Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.

В работе «О многоугольниках и многогранниках» (1810) Пуансо описал четыре правильных звездчатых многогранника, но вопрос о существовании других таких многогранников оставался открытым. Ответ на него был дан год спустя, в 1811 году, французским математиком О. Коши (1789-1857). В работе «Исследование о многогранниках» он доказал, что других правильных звездчатых многогранников не существует.

Кроме правильных звездчатых многогранников существуют и другие звездчатые формы, получающиеся продолжением граней правильных и полуправильных многогранников.

На рисунке 7 изображен многогранник, называемый звездчатым октаэдром.

Продолжения граней кубооктаэдра приводят к четырем звездчатым многогранникам. Первый из них (рис. 8а) получается достраиванием на гранях кубооктаэдра пирамид и представляет собой соединение куба и октаэдра.

Следующая звездчатая форма кубооктаэдра представлена на рисунке 8б. Она образована из соединения куба и октаэдра добавлением 24 бипирамид.

Третья звездчатая форма кубооктаэдра (рис. 8в) представляет собой соединение шести четырехугольных пирамид, основаниями которых служат квадраты.

Последняя звездчатая форма кубооктаэдра (рис. 8г) является соединением звезды Кеплера и трех правильных четырехугольных призм, общей частью которых служит исходный куб.

Икосододекаэдр имеет 19 звездчатых форм, некоторые из которых представлены на рисунке 9.

Источник

Многогранники — виды, свойства и формулы

Основные понятия

Определение многогранника включает в себя такое понятие, как геометрическое тело, созданное из плоских многоугольников. Их число конечное. От формы каждого из них напрямую зависят свойства итоговой фигуры. Их делят на 2 типа:

Поскольку многогранники рассматриваются в трехмерном евклидовом пространстве, они относятся к стереометрии. А их многоугольники лежат в двумерной плоскости, что относится к планиметрии. Поэтому основные свойства и понятия формируются, включая в себя обе эти науки.

Параметры фигуры

Правильные многогранники

Правильные многогранники — фигуры, грани которых представляют собой многоугольники с равными углами и сторонами. Также они называются Платоновыми телами. Всего существует 5 соответствующих тел, подробные характеристики которых представлены в таблице.

Правильные многогранники изучались древними греками. Однако первые модели в орнаменте и по отдельности появились намного раньше. Например, археологами были найдены вырезанные каменные шары в Шотландии, которые датируются поздним неолитом (соответственно, за 1000 лет до жизни и деятельности Платона).

Призма и ее особенности

Геометрическое тело называют прямым, если каждое ребро лежит перпендикулярно основанию. Также они становятся высотами. Когда грани идентичны, многоугольник считается правильным, и его диагональное сечение образует параллелограмм.

Характеристики параллелепипеда

Параллелепипед — многогранник, основанием и гранями которого является параллелограмм. Фигура характеризуется как неправильная. Основные характеристики:

Когда все грани параллелограмма являются прямоугольными, фигура характеризуется, как прямоугольная. Длина каждого ребра считается линейным размером. У такой фигуры есть три измерения. При этом справедлива формула d² = a² + b² + c². При расчетах руководствуются и другими. Для объема : V = abc, для площади многогранника: S=2·(ab+ bc +ac).

Пирамида и ее величины

Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:

Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.

Источник