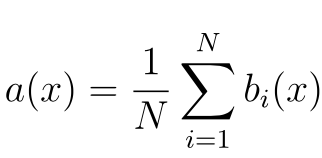что плохого в случайных лесах random forest
Алгоритм классификации Random Forest на Python
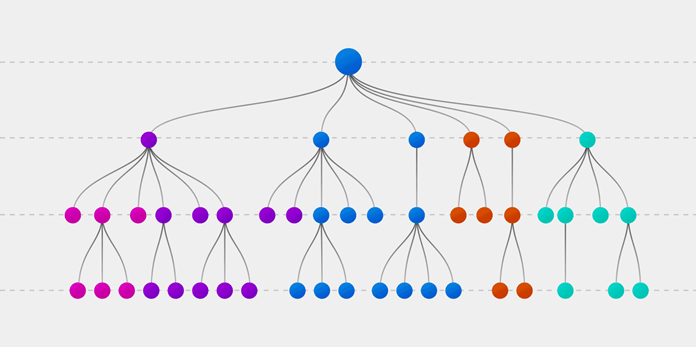
Случайный лес (Random forest, RF) — это алгоритм обучения с учителем. Его можно применять как для классификации, так и для регрессии. Также это наиболее гибкий и простой в использовании алгоритм. Лес состоит из деревьев. Говорят, что чем больше деревьев в лесу, тем он крепче. RF создает деревья решений для случайно выбранных семплов данных, получает прогноз от каждого дерева и выбирает наилучшее решение посредством голосования. Он также предоставляет довольно эффективный критерий важности показателей (признаков).
Случайный лес имеет множество применений, таких как механизмы рекомендаций, классификация изображений и отбор признаков. Его можно использовать для классификации добросовестных соискателей кредита, выявления мошенничества и прогнозирования заболеваний. Он лежит в основе алгоритма Борута, который определяет наиболее значимые показатели датасета.
Алгоритм Random Forest
Давайте разберемся в алгоритме случайного леса, используя нетехническую аналогию. Предположим, вы решили отправиться в путешествие и хотите попасть в туда, где вам точно понравится.
Итак, что вы делаете, чтобы выбрать подходящее место? Ищите информацию в Интернете: вы можете прочитать множество различных отзывов и мнений в блогах о путешествиях, на сайтах, подобных Кью, туристических порталах, — или же просто спросить своих друзей.
Предположим, вы решили узнать у своих знакомых об их опыте путешествий. Вы, вероятно, получите рекомендации от каждого друга и составите из них список возможных локаций. Затем вы попросите своих знакомых проголосовать, то есть выбрать лучший вариант для поездки из составленного вами перечня. Место, набравшее наибольшее количество голосов, станет вашим окончательным выбором для путешествия.
Вышеупомянутый процесс принятия решения состоит из двух частей.
Технически Random forest — это метод (основанный на подходе «разделяй и властвуй»), использующий ансамбль деревьев решений, созданных на случайно разделенном датасете. Набор таких деревьев-классификаторов образует лес. Каждое отдельное дерево решений генерируется с использованием метрик отбора показателей, таких как критерий прироста информации, отношение прироста и индекс Джини для каждого признака.
Любое такое дерево создается на основе независимой случайной выборки. В задаче классификации каждое дерево голосует, и в качестве окончательного результата выбирается самый популярный класс. В случае регрессии конечным результатом считается среднее значение всех выходных данных ансамбля. Метод случайного леса является более простым и эффективным по сравнению с другими алгоритмами нелинейной классификации.
Как работает случайный лес?
Алгоритм состоит из четырех этапов:
Поиск важных признаков
Random forest также предлагает хороший критерий отбора признаков. Scikit-learn предоставляет дополнительную переменную при использовании модели случайного леса, которая показывает относительную важность, то есть вклад каждого показателя в прогноз. Библиотека автоматически вычисляет оценку релевантности каждого признака на этапе обучения. Затем полученное значение нормализируется так, чтобы сумма всех оценок равнялась 1.
Такая оценка поможет выбрать наиболее значимые показатели и отбросить наименее важные для построения модели.
Случайный лес использует критерий Джини, также известный как среднее уменьшение неопределенности (MDI), для расчета важности каждого признака. Кроме того, критерий Джини иногда называют общим уменьшением неопределенности в узлах. Он показывает, насколько снижается точность модели, когда вы отбрасываете переменную. Чем больше уменьшение, тем значительнее отброшенный признак. Таким образом, среднее уменьшение является необходимым параметром для выбора переменной. Также с помощью данного критерия можете быть отображена общая описательная способность признаков.
Сравнение случайных лесов и деревьев решений
Создание классификатора с использованием Scikit-learn
Вы будете строить модель на основе набора данных о цветках ириса, который является очень известным классификационным датасетом. Он включает длину и ширину чашелистика, длину и ширину лепестка, и тип цветка. Существуют три вида (класса) ирисов: Setosa, Versicolor и Virginica. Вы построите модель, определяющую тип цветка из вышеперечисленных. Этот датасет доступен в библиотеке scikit-learn или вы можете загрузить его из репозитория машинного обучения UCI.
Анализ малых данных
КвазиНаучный блог Александра Дьяконова
Случайный лес (Random Forest)
Случайный лес — один из самых потрясающих алгоритмов машинного обучения, придуманные Лео Брейманом и Адель Катлер ещё в прошлом веке. Он дошёл до нас в «первозданном виде» (никакие эвристики не смогли его существенно улучшить) и является одним из немногих универсальных алгоритмов. Универсальность заключается, во-первых, в том, что он хорош во многих задачах (по моим оценкам, 70% из встречающихся на практике, если не учитывать задачи с изображениями), во-вторых, в том, что есть случайные леса для решения задач классификации, регрессии, кластеризации, поиска аномалий, селекции признаков и т.д.
Этот пост — краткое практическое руководство для новичков — путеводитель по основным параметрам алгоритма с картинками (которые, кстати, построены на данных последнего конкурса Сбербанка и одной модельной задачи). Под тестом здесь понимается результат на скользящем контроле (для построения графиков использовано 5 фолдов), хотя для отложенного контроля (hold out) выводы будут такими же. Графики лежат в коридорах: дисперсионном и (если есть второй коридор) макс-минном. Все выводы и рекомендации — общие — не для конкретной задачи.
RF (random forest) — это множество решающих деревьев. В задаче регрессии их ответы усредняются, в задаче классификации принимается решение голосованием по большинству. Все деревья строятся независимо по следующей схеме:
Понятно, что такая схема построения соответствует главному принципу ансамблирования (построению алгоритма машинного обучения на базе нескольких, в данном случае решающих деревьев): базовые алгоритмы должны быть хорошими и разнообразными (поэтому каждое дерево строится на своей обучающей выборке и при выборе расщеплений есть элемент случайности).
В библиотеке scikit-learn есть такая реализация RF (привожу только для задачи классификации):
С алгоритмом работают по стандартной схеме, принятой в scikit-learn:
Опишем, что означают основные параметры:
Число деревьев — n_estimators
Чем больше деревьев, тем лучше качество, но время настройки и работы RF также пропорционально увеличиваются. Обратите внимание, что часто при увеличении n_estimators качество на обучающей выборке повышается (может даже доходить до 100%), а качество на тесте выходит на асимптоту (можно прикинуть, скольких деревьев Вам достаточно).
Число признаков для выбора расщепления — max_features
График качества на тесте от значения этого праметра унимодальный, на обучении он строго возрастает. При увеличении max_features увеличивается время построения леса, а деревья становятся «более однообразными». По умолчанию он равен sqrt(n) в задачах классификации и n/3 в задачах регрессии. Это самый важный параметр! Его настраивают в первую очередь (при достаточном числе деревьев в лесе).
Минимальное число объектов, при котором выполняется расщепление — min_samples_split
Этот параметр, как правило, не очень важный и можно оставить значение по умолчанию (2). График качества на контроле может быть похожим на «расчёску» (нет явного оптимума). При увеличении параметра качество на обучении падает, а время построения RF сокращается.
Ограничение на число объектов в листьях — min_samples_leaf
Всё, что было описано про min_samples_split, годится и для описания этого параметра. Часто можно оставить значение по умолчанию (1). Кстати, по классике, в задачах регрессии рекомендуется использовать значение 5 (в библиотеке randomForest для R так и реализовано, в sklearn — 1).
Максимальная глубина деревьев — max_depth
Ясно, что чем меньше глубина, тем быстрее строится и работает RF. При увеличении глубины резко возрастает качество на обучении, но и на контроле оно, как правило, увеличивается. Рекомендуется использовать максимальную глубину (кроме случаев, когда объектов слишком много и получаются очень глубокие деревья, построение которых занимает значительное время). При использовании неглубоких деревьев изменение параметров, связанных с ограничением числа объектов в листе и для деления, не приводит к значимому эффекту (листья и так получаются «большими»). Неглубокие деревья рекомендуют использовать в задачах с большим числом шумовых объектов (выбросов).
Критерий расщепления — criterion
По смыслу это очень важный параметр, но по факту здесь нет вариантов выбора. В библиотеке sklearn для регрессии реализованы два критерия: “mse” и “mae”, соответствуют функциям ошибки, которые они минимизируют. В большинстве задач используется mse. Сравнить их пока не берусь, т.к. mae появился совсем недавно — в версии 0.18 (и по-моему, реализован с ошибкой). Для классификации реализованы критерии “gini” и “entropy”, которые соответствуют классическим критериям расщепления: Джини и энтропийному. Простой перебор поможет Вам выбрать, что использовать в конкретной задаче (в авторской реализации алгоритма использовался Джини). Подробнее о критериях надо писать отдельный пост;)
В sklearn-реализации случайного леса нет параметра samplesize, который регламентирует, из скольких объектов делать подвыборку для построения каждого дерева. Такой параметр есть в R-реализации, но, по сути, часто оптимально выбирать из всей выборки. Также рекомендуется выбирать подвыборку с возвращением: bootstrap=True (это и есть бэггинг — bootstrap aggregating).
Совет
По умолчанию в sklearn-овских методах n_jobs=1, т.е. случайный лес строится на одном процессоре. Если Вы хотите существенно ускорить построение, используйте n_jobs=-1 (строить на максимально возможном числе процессоров). Для построения воспроизводимых экспериментов используйте предустановку генератора псевдослучайных чисел: random_state.
П.С. Метод RF хорош ещё тем, что при построении леса параллельно может вычисляться т.н. oob-оценка качества алгоритма (которая очень точная и получается не в ущерб разделения на обучение/тест), oob-ответы алгоритмы (ответы, которые выдавал бы алгоритм на обучающей выборке, если бы «обучался не на ней»), оцениваются важности признаков (но об этом, опять же, надо писать в отдельном посте). Ну, и не стоит забывать про полный перебор значений параметров (если объектов в задаче не очень много).
🤖 Машинное обучение для начинающих: алгоритм случайного леса (Random Forest)
Alex Maszański
В каких задачах используется?
Благодаря своей гибкости Random Forest применяется для решения практически любых проблем в области машинного обучения. Сюда относятся классификации (RandomForestClassifier) и регрессии (RandomForestRegressor), а также более сложные задачи, вроде отбора признаков, поиска выбросов/аномалий и кластеризации.
Основным полем для применения алгоритма случайного дерева являются первые два пункта, решение других задач строится уже на их основе. Так, для задачи отбора признаков мы осуществляем следующий код:
Здесь мы на основе классификации просто добавляем метод для отбора признаков.
Порядок действий в алгоритме
Теоретическая составляющая алгоритма случайного дерева
По сравнению с другими методами машинного обучения, теоретическая часть алгоритма Random Forest проста. У нас нет большого объема теории, необходима только формула итогового классификатора a(x) :
Стоит также отметить, что для задачи классификации мы выбираем решение голосованием по большинству, а в задаче регрессии – средним.
Реализация алгоритма Random Forest
Реализуем алгоритм на простом примере для задачи классификации, используя библиотеку scikit-learn:
Работаем с алгоритмом по стандартному порядку действий, принятому в scikit-learn. Вычисляем AUC-ROC (площадь под кривой ошибок) для тренировочной и тестовой частей модели, чтобы определить ее качество:
Необходимые параметры алгоритма
Число деревьев – n_estimators
Критерий расщепления – criterion
Простой метод перебора поможет выбрать, что использовать для решения конкретной проблемы.
Число признаков для выбора расщепления – max_features
Минимальное число объектов для расщепления – min_samples_split
Второстепенный по своему значению параметр, его можно оставить в состоянии по умолчанию.
Ограничение числа объектов в листьях – min_samples_leaf
Максимальная глубина деревьев – max_depth
Чем меньше максимальная глубина, тем быстрее строится и работает алгоритм случайного дерева.
Неглубокие деревья рекомендуется использовать в задачах со значительным количеством шумовых объектов (выбросов).
Преимущества алгоритма
Недостатки алгоритма
Заключение
Метод случайного дерева (Random Forest) – это универсальный алгоритм машинного обучения с учителем. Его можно использовать во множестве задач, но в основном он применяется в проблемах классификации и регрессии.
Вы можете использовать случайный лес, если вам нужны чрезвычайно точные результаты или у вас есть огромный объем данных для обработки, и вам нужен достаточно сильный алгоритм, который позволит вам эффективно обработать все данные.
Random Forest: прогулки по зимнему лесу
1. Вступление
Это небольшое практическое руководство по применению алгоритмов машинного обучения. Разумеется, существует немалое число алгоритмов машинного обучения и способов математического (статистического) анализа информации, однако, эта заметка посвящена именно Random Forest. В заметке показаны примеры использования этого алгоритма для задач классификации и регрессии, а также даны некоторые теоретические пояснения.
2. Несколько слов о деревьях
Прежде всего, рассмотрим некоторые базовые теоретические принципы работы этого алгоритма, а начнём с такого понятия, как деревья решений. Наша основная задача — принять решение на основе имеющейся информации. В самом простом случае у нас есть всего один признак (метрика, предиктор, регрессор) с хорошо различимыми границами между классов (максимальное значение для одного класса явно меньше минимального значения для другого). Например, зная массу тела нужно отличить кита от пчелы, если известно, что среди всех наблюдений нет ни одного кита, который бы имел массу тела как у пчелы. Следовательно, достаточно всего одного показателя (предиктора), чтобы дать точный ответ, предсказав тем самым верный класс.
Допустим, что точки одного класса (пусть они будут показаны красным цветом) во всех наблюдениях находятся выше точек синего цвета. Человек может провести между ними прямую линию и сказать, что это и будет граница классов. Следовательно, всё расположенное выше этой границы будет относиться к одному классу, а всё ниже линии — к другому.
Отобразим это в виде древовидной структуры. Если мы воспользуемся одним из алгоритмов (CART) для создания дерева решений по указанным ранее данным, то получим следующее условие классификации:
Следовательно, его визуальное представление будет таким:
Разумеется, каждый признак обладает разной степенью важности. Из следующего набора данных (формат LibSVM) видно, что первый признак (его индекс 1, так как нумерация начинается не с нуля) абсолютно идентичен у представителей всех классов. Фактически, этот показатель не имеет никакой ценности для классификации, следовательно, его можно назвать избыточной информацией, которая не несёт никакой практической пользы. Аналогичная ситуация и со вторым признаком (предиктором). Однако, третий из них отличается.
Именно третий признак (feature 2) и будет служить тем самым заветным различием, с помощью которого можно предсказывать класс по вектору. Логично предположить, что задача может быть решена одним единственным условием (If-Else). Действительно, каждое дерево в алгоритме машинного обучения правильно смогло понять различия. Далее показана отладочная информация (использован классификатор Random Forest из фреймворка Apache Spark 2.1.0) для нескольких деревьев ансамбля случайного леса.
Для более сложных задач необходимы более сложные деревья. В следующем примере закономерность перестала быть такой очевидной для человека. Нужно более внимательно посмотреть набор данных, чтобы заметить различия. Условие будет немного более сложным, так как нужна дополнительная проверка.
Вот такие дополнительные проверки требуют новых ветвлений (узлов) дерева. После каждого ветвления необходимо будет делать ещё проверки, т.е. новые ветвления. Это видно на отладочной информации. В целях экономии места я привожу только несколько деревьев:
А теперь представим себе набор данных из миллиона строк и из нескольких сотен (даже тысяч) столбцов. Согласитесь, что простыми условиями такие задачи будет сложно решить. Более того, при очень сложных условиях (глубокое дерево) оно может быть слишком специфично для конкретного набора данных (переобучено). Одно дерево стойко к масштабированию данных, но не стойко к шумам. Если объединить большое количество деревьев в одну композицию, то можно получить значительно более хорошие результаты. В итоге получается весьма эффективная и достаточно универсальная модель.
3. Random Forest
По сути, Random Forest является композицией (ансамблем) множества решающих деревьев, что позволяет снизить проблему переобучения и повысить точность в сравнении с одним деревом. Прогноз получается в результате агрегирования ответов множества деревьев. Тренировка деревьев происходит независимо друг от друга (на разных подмножествах), что не просто решает проблему построения одинаковых деревьев на одном и том же наборе данных, но и делает этот алгоритм весьма удобным для применения в системах распределённых вычислений. Вообще, идея бэггинга, предложенная Лео Брейманом, хорошо подходит для распределения вычислений.
Для бэггинга (независимого обучения алгоритмов классификации, где результат определяется голосованием) есть смысл использовать большое количество деревьев решений с достаточно большой глубиной. Во время классификации финальным результатом будет тот класс, за который проголосовало большинство деревьев, при условии, что одно дерево обладает одним голосом.
Так, например, если в задаче бинарной классификации была сформирована модель с 500 деревьями, среди которых 100 указывают на нулевой класс, а остальные 400 на первый класс, то в результате модель будет предсказывать именно первый класс. Если использовать Random Forest для задач регрессии, то подход выбора того решения, за которое проголосовало большинство деревьев будет неподходящим. Вместо этого происходит выбор среднего решения по всем деревьям.
Random Forest (по причине независимого построения глубоких деревьев) требует весьма много ресурсов, а ограничение на глубину повредит точности (для решения сложных задач нужно построить много глубоких деревьев). Можно заметить, что время обучения деревьев возрастает приблизительно линейно их количеству.
Естественно, увеличение высоты (глубины) деревьев не самым лучшим образом сказывается на производительности, но повышает эффективность этого алгоритма (хотя и вместе с этим повышается склонность к переобучению). Слишком сильно бояться переобучения не следует, так как это будет скомпенсировано числом деревьев. Но и увлекаться тоже не следует. Везде важны оптимально подобранные параметры (гиперпараметры).
Рассмотрим пример классификации на языке программирования R. Так как нам сейчас нужна классификационная модель, а не регрессионная, то в качестве первого параметра следует явно задать, что класс является именно фактором. Кроме количества деревьев уделим внимание числу признаков (mtry), которое будет использовать элементарная модель (дерево) для ветвлений. Фактически, это два основных параметра, которые есть смысл настраивать в первую очередь.
Убедимся, что это именно модель для классификации:
Ознакомимся с результатами confusion matrix:
Интересно увидеть предсказанные значения (на основе out-of-bag):
А функции varImpPlot и importance предназначены для отображения важности предикторов (ценности для точности работы классификатора).
Разумеется, для получения вероятного класса существует специальная функция. Она называется predict. В качестве первого аргумента требует модель, а в качестве второго — набор данных. Результатом будет вектор предсказанных классов. Для надёжной проверки необходимо выполнять тренировку на одном наборе данных, а проверку на другом наборе данных.
Ещё один пример. На этот раз используем Apache Spark 2.1.0 и язык программирования Scala. Информацию мы прочитаем из файла формата LibSVM. После этого необходимо будет явно разделить набор данных на две части. Одна из них будет учебная, а вторая — проверочная. Выполнять стандартизацию или нормализацию нет особого смысла. Наша модель устойчива к этому, равно как и достаточно устойчива к данным различной природы (вес, возраст, доход).
Повторюсь, что обучение необходимо производить только на учебной выборке. Количество классов в этом примере будет равно двум. Количество деревьев пусть будет 50. Оставим индекс Джинни в качестве критерия расщепления, так как теоретически применение энтропии не будет значительно более эффективным критерием. Глубину дерева ограничим девятью.
Теперь используем тестовый набор данных, чтобы проверить работу классификатора с указанными параметрами. Следует заметить, что порог точности (пригодность модели) определяется индивидуально в каждом конкретном случае.
Получив на вход вектор предикторов, система должна угадать (с допустимой вероятностью) класс объекта. Если в результате нескольких проверок на большом наборе данных это удалось сделать, то можно утверждать о точности модели. Однако, никакой человек и никакая система не смогут угадать с очень высокой точностью по росту человека его уровень образования. Следовательно, без правильно собранных и подготовленных данных сложно (или вообще невозможно) будет решить задачу.
4. Несколько мыслей о практическом применении
Бывают такие ситуации, когда простым условием или методами описательной статистики задачу сходу решить не получается. Как раз в задачах повышения эффективности интернет-проектов (анализ клиентов, выявление вероятности покупки, оптимальные стратегии рекламы, выбор товаров для показа в популярных блоках, рекомендации и персональные ранжирования, классификация записей в каталогах и справочниках) и встречаются подобные сложные наборы данных.
Помню, несколько лет назад впервые столкнулся с необходимостью применения ML-технологий. Была ситуация, когда мы с коллегами (группа разработчиков) пытались придумать метод классификации материалов подробного справочника на очень большом портале. Раньше классификация выполнялась вручную другими специалистами, что требовало огромного количества времени. А вот автоматизировать никак не получалось (правила и статистические методы не дали нужной точности). У нас уже был набор векторов, который ранее разметили специалисты.
Тогда меня удивило, что несколько строк кода (применение одной из популярных библиотек машинного обучения) смогли решить проблему буквально сразу. Естественно, что изучалась возможность применения различных моделей (включая нейронные сети) и продумывались рациональные гиперпараметры. Но так как эта заметка про случайный лес, то пример на языке программирования Python будет посвящён именно ему. Естественно, код примера написан с учётом новых версий готовых классификаторов, а не используемых тогда:
Таких примеров очень много. Расскажу ещё одну историю. Была задача повысить эффективность огромной системы управления рекламой. Её работа напрямую зависела от точности предсказания рейтинга товаров и услуг. У каждого из них был вектор из 64-ти признаков. Стратегически важно было заранее дать относительно точный прогноз значения рейтинга для каждого нового вектора признаков. До этого система управлялась нехитрыми правилами и описательной статистикой. Но, как известно, эффективности и точности в таких вопросах много не бывает. Для решения задачи повышения эффективности была использована регрессионная модель, похожая на указанную в примере:
В итоге мы получаем достаточно мощный инструментарий анализа информации, который способен прийти на помощь в тех задачах, где другие методы дают не самые лучшие результаты.