Что такое числовая функция

Числовая функция

В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел или множества комплексных чисел .

Содержание

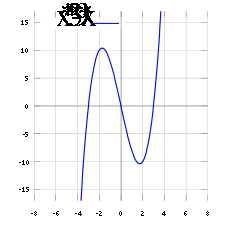
График функции

Примеры

Способы задания функции

Словесный	С помощью естественного языка	Игрек равно целая часть от икс.
Аналитический	С помощью формулы и стандартных обозначений
Графический	С помощью графика
Табличный	С помощью таблицы значений	x 0 1 2 3 4 5 6 7 8 9 y 1 1 2 3 5 8 13 21 34 55

Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента.

Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:

Графический способ

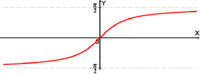
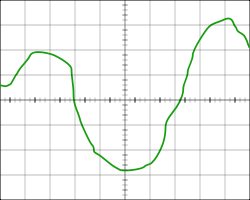
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.

Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

Словесный способ

Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.

Классы числовых функций

Исторический очерк

Появление понятия

Математический термин «функция» впервые появился в 1673 году у Лейбница, и притом не совсем в современном его понимании: Лейбниц вначале называл функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). Позже, однако, в переписке с Иоганном Бернулли (1694) содержание термина расширяется и в конце концов становится синонимом «аналитически заданной зависимости».

В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.

Первые попытки определения

В начале XVIII века были получены разложения всех стандартных функций и многих других. Благодаря, в основном, Эйлеру (1748) были уточнены их определения. Эйлер впервые ясно определил показательную функцию, а также логарифмическую как обратную к ней, и дал их разложения в ряд. До Эйлера многие математики считали, например, тангенс тупого угла положительным; Эйлер дал современные определения всех тригонометрических функций (сам термин «тригонометрическая функция» предложил Клюгель в 1770 году).

В приложениях анализа появляется множество новых трансцендентных функций. Когда Гольдбах и Бернулли попытались найти непрерывный аналог факториала, молодой Эйлер сообщил в письме Гольдбаху о свойствах гамма-функции (1729, название принадлежит Лежандру). Через год Эйлер открыл бета-функцию, и далее неоднократно возвращался к этой теме. Гамма-функция и связанные с ней (бета, дзета, цилиндрические (Бесселя)) находят многочисленные применения в анализе, а также в теории чисел, а дзета-функция Римана оказалась незаменимым инструментом для изучения распределения простых чисел в натуральном ряду.

В 1757 году Винченцо Риккати, исследуя секторы гиперболы, вводит гиперболические функции ch, sh (именно с такими обозначениями) и перечисляет их основные свойства. Немало новых функций возникло в связи с неинтегрируемостью различных выражений. Эйлер определил (1768) интегральный логарифм (название предложил И. Зольднер, 1809), Л. Маскерони — интегральные синус и косинус (1790). Вскоре появляется и новый раздел математики: специальные функции.

С этим пёстрым собранием надо было что-то делать, и математики приняли радикальное решение: все функции, независимо от их происхождения, были объявлены равноправными. Единственное требование, предъявляемое к функции — определённость, причём имеется в виду не однозначность самой функции (она может быть и многозначной), а недвусмысленность способа вычисления её значений.

Первое общее определение функции встречается у Иоганна Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств».

Всё же в XVIII веке отсутствовало достаточно ясное понимание различия между функцией и её аналитическим выражением. Это нашло отражение в той критике, которой Эйлер подверг решение задачи о колебании струны, предложенное Бернулли (1753). В основе решения Бернулли лежало утверждение о возможности разложить любую функцию в тригонометрический ряд. Возражая против этого, Эйлер указал на то, что подобная разложимость доставляла бы для любой функции аналитическое выражение, в то время как функция может и не иметь его (она может быть задана графиком, «начертанным свободным движением руки»).

Под влиянием теории бесконечных рядов, которые давали алгебраическое представление почти любой гладкой зависимости, наличие явной формулы постепенно перестало быть обязательным для функции. Логарифм или показательная функция, например, вычисляются как пределы бесконечных рядов; такой подход распространился и на другие нестандартные функции. С рядами стали обращаться как с конечными выражениями, первоначально никак не обосновывая корректность операций и даже не гарантируя сходимость ряда.

Начиная с «Дифференциального исчисления» (1755), Эйлер фактически принимает современное определение числовой функции как произвольного соответствия чисел [3] :

Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых.

Общее определение

В «Аналитической теории тепла» Фурье (1822) имеется фраза: «Функция обозначает функцию совершенно произвольную, то есть последовательность данных значений, подчинённых или нет общему закону и соответствующих всем значениям , содержащимся между и какой-либо величиной ».

Близко к современному и определение Лобачевского:

…Общее понятие функции требует, чтобы функцией от называть число, которое даётся для каждого и вместе с постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной… Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе.

Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое Дирихле, неоднократно предлагалось и до него. Вот определение Дирихле (1837):

у есть функция переменной х (на отрезке ), если каждому значению х (на этом отрезке) соответствует совершенно определённое значение у, причем безразлично, каким образом установлено это соответствие — аналитической формулой, графиком, таблицей, либо даже просто словами.

К концу XIX века понятие функции перерастает рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.

Примеры

Неявные функции

Функции могут быть заданы при помощи других функций и уравнений.

Предположим, задана функция двух переменных, которая удовлетворяет специальным условиям (условиям теоремы о неявных функций), тогда уравнение вида.

.

определяет неявную функцию вида .

Источник

Числовая функция

Содержание

График функции

Фрагмент графика функции

Способы задания функции

Фрагмент графика функции .

Словесный	С помощью естественного языка	Игрек равно целая часть от х.
Аналитический	С помощью аналитической формулы
Графический	С помощью графика
Табличный	С помощью таблицы значений	x 0 1 2 3 4 5 6 7 8 9 y 1 1 2 3 5 8 13 21 34 55

Классы числовых функций1

Исторический очерк

Математическое моделирование явлений и законов природы приводит к возникновению понятия функции, которое поначалу ограничивается алгебраическими функциями ( многочленами ) и тригонометрией.

Однако в работе Ферма «Введение и изучение плоских и телесных мест» (1636, опубликована в 1679 году ) говорится: «Всякий раз, когда в заключительном уравнении имеются две неизвестные величины, налицо имеется место». По существу здесь идёт речь о функциональной зависимости и её графическом изображении («место» у Ферма означает линию).

У Барроу («Лекции по геометрии», 1670) в геометрической форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует уже о совершенно отчётливом владении понятием функции.

В геометрическом и механическом виде это понятие мы находим и у Ньютона. Сам термин «функция» впервые появляется в 1692 году у Лейбница, и притом не совсем в современном его понимании. Лейбниц вначале называет функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). Позже, однако, в переписке с Иоганном Бернулли (1694) содержание термина расширяется и в конце концов становится синонимом «аналитически заданной зависимости».

В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.

С этим пёстрым собранием надо было что-то делать, и математики приняло радикальное решение: все функции, независимо от их происхождения, были объявлены равноправными. Единственное требование, предъявляемое к функции — определённость, причём имеется в виду не однозначность самой функции (она может быть и многозначной), а недвусмысленность способа вычисления её значений.

Первое общее определение функции встречается у Иоганна Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств».

Однако другие аргументы Эйлера уже ошибочны. Например, он считал, что разложение функции в тригонометрический ряд доставляет для неё единое аналитическое выражение, в то время как она может быть «смешанной» функцией, представимой на разных отрезках разными формулами. На самом деле одно другому не противоречит, но в ту эпоху казалось невозможным, чтобы два аналитических выражения, совпадая на части отрезка, не совпадали на всём его протяжении. Позже, при исследовании функций многих переменных он понял ограниченность прежнего определения и признал разрывные функции, а затем, после исследования комплексного логарифма — даже многозначные функции.

Под влиянием теории бесконечных рядов, которые давали алгебраическое представление почти любой гладкой зависимости, наличие явной формулы постепенно перестало быть обязательным для функции. Логарифм или показательная функция, например, вычисляются как пределы бесконечных рядов; такой подход распространился и на другие нестандартные функции. С рядами обращаются как с конечными выражениями, первоначально никак не обосновывая корректность операций и даже не гарантируя сходимость ряда.

Начиная с «Дифференциального исчисления» (1755), Эйлер фактически принимает современное определение функции как произвольного числового соответствия:

Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых.

С начала XIX века уже всё чаще и чаще определяют понятие функции без упоминания об её аналитическом изображении. В «Трактате по дифференциальному и интегральному исчислению» (1797—1802) Лакруа говорится: «Всякая величина, значение которой зависит от одной или многих других величин, называется функцией этих последних».

В «Аналитической теории тепла» Фурье (1822) имеется фраза: «Функция обозначает функцию совершенно произвольную, то есть последовательность данных значений, подчинённых или нет общему закону и соответствующих всем значениям , содержащимся между и какой-либо величиной ».

Близко к современному и определение Лобачевского:

…Общее понятие функции требует, чтобы функцией от называть число, которое даётся для каждого и вместе с постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной… Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе.

у есть функция переменной х (на отрезке ), если каждому значению х (на этом отрезке) соответствует совершенно определённое значение у, причем безразлично, каким образом установлено это соответствие — аналитической формулой, графиком, таблицей, либо даже просто словами.

Источник

Что такое Функция?

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Что такое числовая функция

зМБЧБ 2. жХОЛГЙС. юЙУМПЧЩЕ ЖХОЛГЙЙ.

ОБЪЩЧБАФ ЮЙУМПЧПК ЖХОЛГЙЕК.

оБРТЙНЕТ, РХУФШ X НОПЦЕУФЧП ФТЕХЗПМШОЙЛПЧ ОБ РМПУЛПУФЙ Й f ЕУФШ РТБЧЙМП, ЛПФПТПЕ ЛБЦДПНХ ФТЕХЗПМШОЙЛХ УФБЧЙФ Ч УППФЧЕФУФЧЙЕ ЮЙУМП, ТБЧОПЕ ДМЙОЕ ТБДЙХУБ r ПРЙУБООПК ПЛПМП ОЕЗП ПЛТХЦОПУФЙ. фПЗДБ НЩ ЙНЕЕН ДЕМП У ЮЙУМПЧПК ЖХОЛГЙЕК, БТЗХНЕОФПН ЛПФПТПК СЧМСЕФУС ФТЕХЗПМШОЙЛ.

ч ДБМШОЕКЫЕН ПУОПЧОПЕ ЧОЙНБОЙЕ ХДЕМСЕФУС ЖХОЛГЙСН, ДМС ЛПФПТЩИ НОПЦЕУФЧБ X Й Y СЧМСАФУС ЮЙУМПЧЩНЙ, Ф.Е.

2.1. уРПУПВЩ ЪБДБОЙС ЖХОЛГЙК.

фБВМЙЮОЩК УРПУПВ ЪБДБОЙС. ьФПФ УРПУПВ УПУФПЙФ Ч ФПН, ЮФП ЖХОЛГЙС y = f (x) ЪБДБЕФУС ФБВМЙГЕК, УПДЕТЦБЭЕК ЪОБЮЕОЙС БТЗХНЕОФБ x Й УППФЧЕФУФЧХАЭЙЕ ЪОБЮЕОЙС ЖХОЛГЙЙ y. оБРТЙНЕТ, ФБВМЙГЩ ФТЙЗПОПНЕФТЙЮЕУЛЙИ ЖХОЛГЙК, ФБВМЙГЩ МПЗБТЙЖНПЧ Й Ф.Д.

зТБЖЙЛ ЮЕФОПК ЖХОЛГЙЙ УЙННЕФТЙЮЕО ПФОПУЙФЕМШОП ПУЙ ПТДЙОБФ, Б ОЕЮЕФОПК ПФОПУЙФЕМШОП ОБЮБМБ ЛППТДЙОБФ. еДЙОУФЧЕООПК ЖХОЛГЙЕК, ПВМБДБАЭЕК УЧПКУФЧПН ЮЕФОПУФЙ Й ОЕЮЕФОПУФЙ ПДОПЧТЕНЕООП СЧМСЕФУС ЖХОЛГЙС y=0

2.2.2. нПОПФПООПУФШ. жХОЛГЙС f ОБЪЩЧБЕФУС ОЕХВЩЧБАЭЕК, ЕУМЙ ДМС МАВЩИ ФБЛЙИ, ЮФП x₁ f (x₂) ; Ф.Е.

2.3. оЕУФБОДБТФОЩЕ ЖПТНЩ ЪБРЙУЙ ЖХОЛГЙК.

2.3.1. пВТБФОБС ЖХОЛГЙС.

. жХОЛГЙС , ЛПФПТБС УФБЧЙФ Ч УППФЧЕФУФЧЙЕ ЛБЦДПНХ ЬМЕНЕОФХ ЬМЕНЕОФ ФБЛПК, ЮФП y=f (x) ОБЪЩЧБЕФУС ПВТБФОПК Л f:

2.3.2. уМПЦОБС ЖХОЛГЙС.

йОПЗДБ ЧПЪОЙЛБАФ УМХЮБЙ, ЛПЗДБ ОЕЧПЪНПЦОП ЙМЙ ОЕ ГЕМЕУППВТБЪОП ЙУЛБФШ БОБМЙФЙЮЕУЛПЕ ЧЩТБЦЕОЙЕ УХЭЕУФЧХАЭЕК ЖХОЛГЙПОБМШОПК ЪБЧЙУЙНПУФЙ. фПЗДБ ЙУРПМШЪХАФУС ДТХЗЙЕ ЖПТНЩ ЪБРЙУЙ ЖХОЛГЙК.

рХУФШ ЖХОЛГЙПОБМШОБС ЪБЧЙУЙНПУФШ f ПРТЕДЕМСЕФУС ДЧХНС ЙМЙ ОЕУЛПМШЛЙНЙ БОБМЙФЙЮЕУЛЙНЙ ЧЩТБЦЕОЙСНЙ.

фПЗДБ ЖХОЛГЙС , ОБЪЩЧБЕФУС УМПЦОПК ЖХОЛГЙЕК ЙМЙ ЛПНРПЪЙГЙЕК ЖХОЛГЙК F Й .

рТЙНЕТ: дБОБ ЖХОЛГЙС , РТЙЮЕН . оБКФЙ ЖХОЛГЙА .

йФБЛ, УМПЦОБС ЖХОЛГЙС . ъБНЕФЙН, ЮФП ОЕ ЧУСЛБС УПЧПЛХРОПУФШ БОБМЙФЙЮЕУЛЙИ ЧЩТБЦЕОЙК ПРТЕДЕМСЕФ ЖХОЛГЙА, ОБРТЙНЕТ

2.3. 3. рПУМЕДПЧБФЕМШОПУФШ.

рПУМЕДПЧБФЕМШОПУФШ, ЛБЛ Й МАВПЕ ВЕУЛПОЕЮОПЕ НОПЦЕУФЧП, ОЕЧПЪНПЦОП ЪБДБФШ РХФЕН РЕТЕЮЙУМЕОЙС ЧУЕИ ЕЈ ЬМЕНЕОФПЧ, РПЬФПНХ УБНЩК РТПУФПК УРПУПВ ЪБДБОЙС РПУМЕДПЧБФЕМШОПУФЙ ЬФП ХЛБЪБФШ, Ч СЧОПН ЧЙДЕ, ЪБЧЙУЙНПУФШ ЬМЕНЕОФБ РПУМЕДПЧБФЕМШОПУФЙ ПФ ЕЗП ОПНЕТБ, Ф.Е. ЪБДБОЙЕ «ЖПТНХМЩ ПВЭЕЗП ЮМЕОБ» Ч ЧЙДЕ x_n=f (n).

1) ;

2) ;

3) ;

4) ФБЛХА РПУМЕДПЧБФЕМШОПУФШ ОБЪЩЧБАФ УФБГЙПОБТОПК;

5) .

дТХЗЙН УРПУПВПН ЪБДБОЙС РПУМЕДПЧБФЕМШОПУФЙ УМХЦЙФ УРПУПВ, ЛПФПТЩК ОБЪЩЧБЕФУС ТЕЛХТТЕОФОЩН. пО УПУФПЙФ Ч ФПН, ЮФП РПУМЕДХАЭЙК ЬМЕНЕОФ РПУМЕДПЧБФЕМШОПУФЙ ЧЩЮЙУМСЕФУС РП РТЕДЩДХЭЕНХ. уХЭЕУФЧХАФ РПУМЕДПЧБФЕМШОПУФЙ, ЛПФПТЩЕ НПЦОП ЪБДБФШ Й ТЕЛХТТЕОФОП Й У РПНПЭША «ЖПТНХМЩ ПВЭЕЗП ЮМЕОБ». ьФП, ОБРТЙНЕТ, БТЙЖНЕФЙЮЕУЛБС Й ЗЕПНЕФТЙЮЕУЛБС РТПЗТЕУУЙЙ.

фБЛ, ЛБЛ МАВБС ЮЙУМПЧБС РПУМЕДПЧБФЕМШОПУФШ ЕУФШ ЖХОЛГЙС ОБФХТБМШОПЗП БТЗХНЕОФБ, ФП НПЦОП ЗПЧПТЙФШ П НПОПФПООПУФЙ Й ПЗТБОЙЮЕООПУФЙ РПУМЕДПЧБФЕМШОПУФЙ.

ъБНЕЮБОЙЕ. нПЦОП РПУФТПЙФШ РПУМЕДПЧБФЕМШОПУФЙ, ЛПФПТЩЕ ОЕ СЧМСАФУС ЮЙУМПЧЩНЙ. оБРТЙНЕТ, ЕУМЙ ЙЪП ДОС Ч ДЕОШ РЕТЕРЙУЩЧБФШ РФЙГ, РТПМЕФБАЭЙИ ПЛПМП ПЛОБ, РПМХЮЙН РПУМЕДПЧБФЕМШОПУФШ, ЮМЕОБНЙ ЛПФПТПК УМХЦБФ РФЙГЩ, РТЙФПН ПДОБ Й ФБ ЦЕ РФЙГБ НПЦЕФ ВЩФШ ЪБРЙУБОБ ОЕ ПДЙО ТБЪ. дТХЗЙН РТЙНЕТПН УМХЦЙФ ЛБФБМПЗ ОЕВЕУОЩИ ЪЧЕЪД.

оБЪБД

Источник