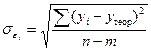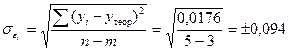Что такое экстраполяция рядов динамики

Экстраполяция в рядах динамики и прогнозирование.

Поможем написать любую работу на аналогичную тему

Применение экстраполяции в прогнозировании базируется на сле­дующих предпосылках:

• развитие исследуемого явления в целом описывается плавной кривой;

• общая тенденция развития явления в прошлом и настоящем не претерпет серьезных изменений в будущем.

Чем короче срок экстраполяции (период упреждения), тем более надежные и точные результаты (при прочих равных условиях) дает прогноз. Экстраполяцию в общем виде можно представить формулой:

1)Прогнозирование по среднему абсолютному приросту может быть Полнено в том случае, если есть уверенность считать общую тенденцию линейной, т.е. метод основан на предположении о равномерном вменении уровня.

номер последнего уровня (года) исследуемого периода, за который рассчитан Д;

срок прогноза (период упреждения);

средний абсолютный прирост.

При ус­ловии:

2) Прогнозирование по среднему темпу роста осуществляется в случае, когда есть основание считать, что общая тенденция ряда ха­рактеризуется показательной (экспоненциальной) кривой.

последний уровень ряда динамики;

средний коэффициент роста.

3) Наиболее распространенным методом прогнозирования считают аналитическое выражение тренда.

Величина доверительного интервала определяется следующим образом:

Источник

ЭКСТРАПОЛЯЦИЯ В РЯДАХ ДИНАМИКИ И ПРОГНОЗИРОВАНИЕ

Определяемые в анализе рядов динамики теоретические показатели имеют широкое применение при прогнозировании. Составление надежных прогнозов динамики спроса и предложения товаров является необходимым условием регулирования рыночных отношений.

Под экстраполяцией понимается распространение выявленных в анализе рядов динамики закономерностей развития изучаемого явления на будущее.

Основой прогнозирования является предположение, что закономерность, действующая внутри анализируемого ряда динамики, сохраняется и в дальнейшем.

Важное значение при экстраполяции имеет продолжительность базисного ряда динамики и сроков прогнозирования.

Установление сроков прогнозирования l зависит от задачи исследования. Но следует иметь в виду, что чем короче сроки упреждения прогноза, тем надежнее результаты экстраполяции.

(9.70)

-средний абсолютный прирост.

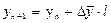
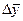
При экстраполяции уровня развития изучаемого явления на базе ряда динамики со стабильными темпами роста (Тр_ц » соnst) применяется формула:

(9.71)

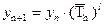
При прогнозировании тренда изучаемого явления на основе аналитического выравнивания применяется адекватная трендовая модель. Так, при выравнивании розничного товарооборота региона в 1993- 1997 гг. (табл. 10.1) была определена на основе показательной функции трендовая модель:

Для прогнозирования возможного уровня развития товарооборота региона в 1998 г. в модель подставляется t = 3.

y₁₉₉₉ = 17,67-1,04 3 = 19,8 млрд. руб.

На практике результат экстраполяции прогнозируемых уровней социально-экономических явлений обычно выполняется не дискретными, а интервальными оценками. Для определения границ интервалов используется формула

(9.72)

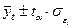
где 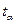— коэффициент доверия по распределению Стьюдента;

Применение формулы (9.72) проиллюстрируем на данных экстраполяции объема розничного товарооборота региона в 1998 г.

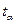
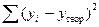
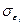
Число степеней свободы при n = 5 и m = 3 составляет 2. При уровне значимости a = 0,05 коэффициент доверия по таблице Стьюдента равен 4,3. При =0,0176 (см. гр. 11 табл. 10.2) значение остаточного среднего квадратического отклонения :

Важно иметь в виду, что экстраполяция в рядах динамики носит приближенный и условный характер. Это обусловлено распространением на ряды динамики положений корреляционно-регрессионного анализа выборочных совокупностей.

ИНДЕКСЫ И ИХ ИСПОЛЬЗОВАНИЕ В ЭКОНОМИКО-СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЯХ

В практике статистики индексы наряду со средними величинами являются наиболее распространенными статистическими показателями. С их помощью характеризуется развитие национальной экономики в целом и ее отдельных отраслей.

Необходимость индексов возникла в связи с тем, что в некоторых совокупностях отдельные элементы не подлежат суммированию. Например, было бы бессмысленно для получения общего объема реализации суммировать данные о продаже тканей (в метрах), костюмов (в штуках) обуви (в парах) и т.д. Поэтому для получения обобщающих (суммарных) величин в сложных статистических совокупностях прибегают к индексному методу.

Основой индексного метода является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям.

Способы построения индексов зависят от содержания и методологии изучаемых показателей.

По степени охвата элементов совокупности различают индивидуальные и сводные (общие) индексы.

Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности (например, изменение выпуска легковых автомобилей определенной марки). Индивидуальный индекс обозначается буквой i.

Сводный (общий) индекс отражает изменение по всей совокупности элементов сложного явления. Если индексы охватывают часть совокупности, то их называют групповыми или субиндексами. Например, сводный индекс характеризует динамику объема промышленной продукции. К субиндексам тогда относятся индексы продукции по отдельным отраслям промышленности. Обозначают сводный (общий) индекс буквой I.

Важной особенностью общих индексов является то, что они обладают обобщающими (синтетическими) и аналитическими свойствами.

Синтетическое свойство состоит в соединении (агрегировании) в целое разнородных единиц статистической совокупности.

Аналитическое свойство состоит в определении изменения уровня результативной величины под влиянием изменения индексируемой величины.

Например, величина индекса цен продукции, равная I_р= 1,1536, может быть истолкована в синтетическом значении как величина, указывающая на то, что цены на продукцию возросли в целом на 15,36%, или в 1,1536 раза, а в аналитическом значении, как показатель того, что в связи с изменением цен стоимость продукции (или размер выручки) увеличилась на 15,36%. Второе направление было связано с применением индексного метода для экономического анализа.

Для определения индекса необходимо сопоставить как минимум две величины. При этом различают сравниваемый уровень и уровень, с которым производится сравнение. Здесь возможны два способа расчета индексов — цепной и базисный. Цепные индексы получают путем сопоставления текущих уровней с предшествующим. Таким образом, база сравнения непрерывно меняется. Базисные индексы получают путем сопоставления с уровнем периода, принятого за базу сравнения.

Источник

Экстраполяция в рядах динамики и прогнозирование

Необходимым условием регулирования рыночных отноше­ний является составление надежных прогнозов развития соци­ально-экономических явлений.

Выявление и характеристика трендов и моделей взаимосвязи создают базу для прогнозирования, т. е. для определения ориен­тировочных размеров явлений в будущем. Для этого используют метод экстраполяции.

Экстраполяция это нахождение уровней за пре­делами изучаемого ряда, т. е. продление в будущее тенденции, наблюдавшейся в прошлом (перспективная экстраполяция). По­скольку в действительности тенденция развития не остается не­изменной, то данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятностные оценки.

Экстраполяцию рядов динамики осуществляют различными способами, например, экстраполируют ряды динамики выравни­ванием по аналитическим формулам. Зная уравнение для теоре­тических уровней и подставляя в него значения t за пределами исследованного ряда, рассчитывают для t вероятностные .

На практике результат экстраполяции прогнозируемых явле­ний обычно получают не точечными (дискретными), а интер­вальными оценками.

Для определения границ интервалов используют формулу:

t_α— коэффициент доверия по распределению Стьюдента;

п — число уровней ряда динамики;

т — число параметров адекватной модели тренда (для уравнения

прямой т = 2). Вероятностные границы интервала прогнозируемого явления:

Нужно иметь в виду, что экстраполяция в рядах динамики носит не только приближенный, но и условный характер.

Число степеней свободы — число элементов статистической совокупности, вариация которых свободна (неограничена).

Стьюдент — псевдоним английского математика и статистика Уильяма С. Госсета, разработавшего метод статистических оценок и проверки гипотез t-распределения, не являющегося нормальным.

РЕГРЕССИОННЫЙ АНАЛИЗ СВЯЗНЫХ ДИНАМИЧЕСКИХ РЯДОВ

Многомерные временные ряды, показывающие зависимость результативного признака от одного или нескольких факторных, называютсвязными рядами динамики. Применение методов наименьших квадратов для обработки рядов динамики не требу­ет предположений о законах распределе­ния исходных данных. Но при использовании метода наи­меньших квадратов для обработки связных рядов надо учи­тывать наличие автокорреляции (авторегрессии), которая не учи­тывалась при обработке одномерных рядов динамики, поскольку ее наличие способствовало более плотному и четкому выявле­нию тенденции развития рассматриваемого социально-экономи­ческого явления во времени.

Автокорреляционная зависимость существенна между последующими и предшествующими уровнями ряда ди­намики.

При анализе нескольких взаимо­связанных рядов динамики важно установить наличие и сте­пень их автокорреляции(поскольку классические методы математической ста­тистики применимы лишь в случае независимости отдельных членов ряда между собой).

Различаются два вида автокорреляции:

1) автокорреляция в наблюдениях за одной или более перемен­ными;

2) автокорреляция ошибок или автокорреляция в отклонениях от тренда.

Наличие последней приводит к искажению величин средних квадратических ошибок коэффициентов регрессии, что затрудняет построение доверительных интервалов для коэффициентов рег­рессии, а также проверку их значимости.

Автокорреляцию измеряют при помощинециклического коэффициента автокорреляции, который рассчитывается не только между соседними уровнями, т. е. сдвинутыми на один период, но и между сдвинутыми на любое число единиц времени (L). Этот сдвиг, именуемыйвременным лагом, опреде­ляет и порядок коэффициентов автокорреляции: первого поряд­ка (при L = 1), второго порядка (при L = 2) и т.д.

Формулу коэффициента автокорреляции можно записать следующим образом:

где , — среднее квадратическое отклонение рядов у_t и у_t+1 соот­ветственно.

Если значение последнего уровня (у_n) ряда мало отличается от первого (у₁), то сдвинутый ряд не укорачивается, его можно условно дополнить, принимая у_n = у₁. Тогда у_t = у_t+1 и = , поскольку рассчитываются они для одного и того же ряда. При такой замене, т. е. если _{t t+1} и ,формула коэффици­ента автокорреляции примет вид:

Если ряд динамики состоит из уровней, среднее значение вторых равно нулю ( = 0), то выражение yпрощается:

.

Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение коэффициентов автокор­реляции сопоставляется с табличным (критическим) для 5%-ного или 1%-ного уровня значимости (вероятности допустить ошибку при принятии нулевой гипотезы о независимости уровней ряда).

(Одна из специальных таблиц, в которой определена критическая область проверяемой гипотезы (об отсутствии автокорреляции), составленная Р. Андерсеном в 1942 г., приведена в приложении 12.)

Если фактическое значение коэффициента автокорреляции меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть принята. Когда же фактическое значение боль­ше табличного, можно сделать вывод о наличии автокорреляции в ряду динамики.

Для уменьшения автокорреляции применяют различные мето­ды. Bсе они преследуют цель исключения основной тенден­ции (тренда) из первоначальных данных.

Теоретическое основание применения этого критерия обуслов­лено тем, что в динамических рядах как сами наблюдения, так и отклонения от них распределяются в хронологическом по­рядке.

Источник

Метод экстраполяции

Добавлено в закладки: 0

М етод экстраполяции – это один из главных способов прогноза, который основывается на прогнозировании событий, учитывая анализ показателей, которые имели место в прошлые годы (при этом, не меньше чем за 5 – 8 лет). В данный момент есть приблизительно триста уравнений, которые дают возможность определить тенденции процессов и позволяют оценить линейную простую зависимость явления и квадратичную зависимость.

Экстраполи́рование, экстраполя́ция, (от лат. extrā — снаружи, вне, кроме, за и лат. polire — выправляю, приглаживаю, меняю, изменяю) — это особенный вид аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не меж фиксированными значениями.

Другими словами, экстраполяция — это приближённое определение значений функции в точках, которые лежат вне отрезка, по её значениям в точках.

Методы

Во многих случаях методы экстраполяции похожи с методами интерполяции.

Самый распространённый способ экстраполяции — это параболическая экстраполяция, при которой в точке берётся значение многочлена степени, которая принимает в точке заданные значения. Для параболической экстраполяции применяют интерполяционные формулы.

Применение

Общее значение — это распространение выводов, которые получены из наблюдения над одной частью явления, на его другую часть.

В маркетинге — это распространение выявленных закономерностей развития изучаемого предмета на будущее.

В статистике — это распространение тенденций, установленных в прошлом, на будущий период (экстраполяция во времени используется для перспективных расчетов населения); распространение выборочных данных на прочую часть совокупности, которая не подвергнута наблюдению (экстраполяция в пространстве).

Одним из более распространенных способов краткосрочного прогнозирования экономических явлений — это экстраполяция

Термин “экстраполяция” имеет немного толкований в широком смысле экстраполяция – это способ научного исследования, который заключается в распространении выводов, которые получены из наблюдений за одной частью явления, на а другую его часть В узком смысле – это определение по нескольким данным функции прочих ее значений вне данного ряда за этим рядом.

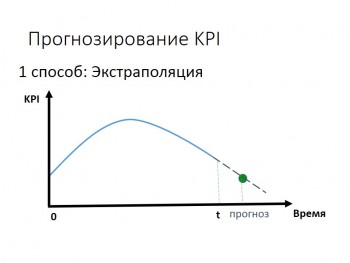
Прогноз экстраполяции

Экстраполяция заключена в изучении сложившихся в настоящем и прошлом устойчивых тенденций экономического развития и их перенос на будущее

Цель данного прогноза — это показать, к каким итогам можно сделать в будущем, когда передвигаться к нему с аналогичной ускорением или скоростью, что и в прошлом

Прогноз определяет ожидаемые варианты данного экономического развития исходя из гипотезы, что главные факторы и тенденции прошлого периода сберегается на период прогноза или что возможно обосновать и учесть направление их изменений в рассматриваемой перспективе. Такую гипотезу выдвигают, учитывая инертность экономических процессов и явлений.

В прогнозировании экстраполяция используется при изучении временных рядов экстраполяции в общем типе можно представить, как определенное значение функции зависимо от особенностей изменения уровней в рядах динамики способы экстраполяции могут быть сложными и простыми.

Простые способы экстраполяции базируются на предположении относительной устойчивости в будущем абсолютных значений уровней, среднего абсолютного прироста, среднего уровня ряда, среднего темпа роста.

Различные способы экстраполяции

Рассмотрим дет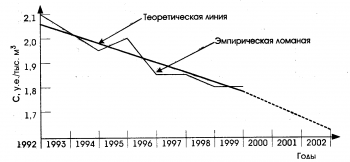альнее названные способы экстраполяции.

При экстраполяции на основании среднего уровня ряда применяется принцип, при котором прогнозируемый уровень равняется среднему значению в прошлом уровней ряда.

В данной ситуации экстраполяция дает точечную прогностическую оценку. Точное совпадение данных оценок с фактическими данными — маловероятное явление. Таким образом, прогноз обязан быть в виде интервала значений.

Полученный доверительный интервал учитывает неопределенность, которая связана с оценкой средней величины, и его использование для прогнозирования увеличивает степень надежности прогноза. Однако недостаток рассматриваемого подходов периода — это то, что доверительный интервал не связывается с периодом предупреждения.

Экстраполяцию по среднему абсолютному приросту можно провести тогда, когда линейной считать общую тенденцию развития явления.

Чтобы рассчитать прогнозное значение, уровень необходимо определить абсолютный средний прирост. Затем, зная уровень ряда динамики, который принимают за основу экстраполяции.

Экстраполяцию по среднему темпу роста можно осуществить, когда есть основания полагать, что суммарная тенденция ряда динамики характеризуется показательной кривой.

Доверительный интервал прогноза по средним темпом роста можно определить лишь в том случае, когда средний темп роста рассчитывают при помощи статистического оценивания параметров экспоненциальной кривой.

Все три рассмотренные способа экстраполяции тренда простейшие, но вместе и самые приближенные.

Сложные способы экстраполяции предусматривают выявление главной тенденции, то есть использование статистических формул, которые описывают тренд.

Способы данной группы возможно разделить на два главных вида: адаптивные и аналитические (кривые роста).

Аналитические способы прогнозирования

В основание аналитических способов прогнозирования (кривых роста) лежит принцип получения при помощи метода самых малых квадратов оценки детерминированной компоненты, которая характеризует главную тенденцию

Адаптивные способы прогнозирования основываются на том, что процесс реализации их заключен в вычислении последовательных во времени значений прогнозируемого показателя, учитывая степень влияния прошлых уровней. К ним относят способы экспоненциальной и текучей средних, способ гармонических весов, способ авторегрессииї.

Способ аналитического выравнивания тренда (способ наименьших квадратов) может быть использован лишь тогда, когда развитие явления довольно хорошо описывают построенную модель и условия, которые определяют тенденцию развития в прошлом, не изменятся существенно в будущем. При выполнении данных требований прогнозирование производится при помощи подстановки в уравнение тренда значений независимой переменной знает величине периода предупреждения.

Процедура создания прогноза по применению аналитического выравнивания тренда включает в себя такие этапы:

1) выбор формы кривой, которая отображает тенденцию;

2) определение показателей, характеризующие количественно тенденции изменений;

3) оценка вероятности прогнозных расчетов

Подбор формы кривой возможно осуществлять на основании построения графика, суммарный тип которого обычно дает возможность установить:

а) имеет динамический ряд показателя выраженную четко тенденцию;

б) если так, то данная тенденция плавная;

в) каков характер тенденции

Отвечая на данные вопросы, нужно помнить, что наружная простота графика ложная. Каждая динамическая задача намного сложнее от статического и каждая точка кривой — это результат изменения явления во времени и пространстве.

Ввиду этого для увеличения достоверности и обоснованности выравнивания для более точного выявления тенденции, которая есть, нужно провести вариантный расчет по некоторым аналитическими функциями и на основании статистических и экспертных оценок определить лучшую форму связей.

На втором этапе нужно определить параметры уравнения связи. Для того, чтобы их найти, применяют способ малых квадратов. В данной ситуации выравнивающая функция будет занимать данное положение среди факт политических значений показателей, при котором общее отклонение точек от функции будет наименьшим.

Обоснованную и достоверную оценку имеющимся результатам можно дать, применяя статистические показатели: средний коэффициент увеличения, коэффициент корреляции, остаточная и общая дисперсия, другой индекс корреляции, коэффициент корреляции ряда отклонений и исходного ряда, определенного по разнице выровненных и фактических по любой аналитической функции.

Для того, чтобы проверить гипотезу об отсутствии или наличии автокорреляции применяют таблицы с критическими значениями коэффициента автокорреляции при разных уровнях значимости. Когда табличное значение коефициэнта автокорреляции больше фактического, то возможно утверждать, что автокорреляция устраняется или отсутствует, а означает, возможно применять формулы для возиожностной оценки значений, которые прогнозируются по этому и точками.

Для прогноза были выбраны такие функции, как логарифмическая, линейная, ступенчатая, полиномиальная и экспоненциальная.

Не все выбранные аналитические функции выравнивают хорошо динамический выходной ряд. Об этом говорит значение индекса (коэффициента) корреляции Для того, чтобы прогнозировать, то есть продолжать сформированные тенденции на ближайшую перспективу, можно использовать лишь те функции, для которых индекс (коэффициент) корреляции больше 0,7 К таковым относят линейную, экспоненциальную и полиномиальную функцию. Последняя имеет самый большой коэффициент корреляции, равен 0,847, и самую малую величину остаточной дисперсией.

Порой, самой приемлемой формой аналитической функции для прогнозирования является полиномиальная функция, которая представлена уравнением:

Подставив в полученное уравнение значения периодов предубеждения, определяем прогнозное значение объема товарооборота на такие три месяца: у25 = 654,83; у = 655,93; у \”- 657,07 тыс грн 26 27

Возможность того, что экономический прогнозируемый показатель в заданный момент времени будет равняться значению, которое отвечает точечной прогноза, почти равняться нулю. Потому к точечному прогнозу границы вероятного изменения прогнозируемого значения показателя.

Заметим, что в полученных при прогнозировании оценок доверительных интервалов необходимо отнестись с осторожностью Это связывается со спецификой динамических рядов Их специфичность заключена в том, что увеличение количества наблюдений в статической совокупности дает возможность получить точные характеристики данной совокупности, в то время как аналогичное удлинение ряда динамики приводит не всегда к похожим результатам, особенно в тех ситуациях, когда ряды динамик применяются для прогнозирования. Данное обстоятельство связывается с тем, что информационная ценность уровней потеряется по мере их удаления от периода предубеждение, то есть означает уровни ряда динамики при прогнозировании неравноценно. Потому параметры уравнений аппроксимирующих кривых роста могут обладать погрешности и изменять собственные оценки при исключении части членов ряда или Анне добавил новых членов ряда динамики, что отображается на точности расчетных значений уровней ряда динамики. Помимо этого, параметры моделей тренда, которые получены способом самых малых квадратов, остаются неизменным и в течение рассматриваемого периода. На практике зачастую встречаются случаи, когда параметры моделей изменяются, а процедуры, которые сглаживают при помощи способа самых малых квадратов не могут определить такие изменения.

Поэтому наиболее эффективными являются адаптивные способы, в которых значимость уровней ряда динамики снижается по мере их удаления от прогнозируемого периода. К ним относят: способ текучих средних, способ экспоненциального сглаживания, способ гармонических весов и прочие, включаются в класс адаптивных способов.

Зачастую несколько динамики характеризуются резкими колебаниями показателей по годам. Данные ряды обычно, имеют слабую связь со временем и не проявляют четкой тенденции к изменению. В данной ситуации способы аналитического выравнивания малоэффективен, потому что возможность расчетов резко уменьшается. Доверительные границы прогноза порой оказываются шире, чем колебания показателя в некоторых динамиках.

При прогнозировании на основании временных рядов, которые весьма колеблются, можно применять способ текучих средних, при помощи которого возможно исключить случайные колебания временного ряда.

Интервал, величина которого все еще постоянная, постепенно помещается на одно наблюдение. Когда наблюдается определенная цикличность изменений показателей, интервал текучести равняется длительности циклу. В ситуации отсутствия цикличности в изменении показателей советуется исполнять различный расчет при параметре сглаживания. Лучший вариант определяется на основании дальнейшей оценки и выровненных рядов.

По данным выровненных значений ряда динамики производится подбор формы кривой, которая отражает тенденции развития явления. Полученное уравнение регрессии применяется для определения прогнозного значения исследуемого показатель.

На основании выровненных значений товарных запасов предприятия имеются такие значения коэффициента корреляции. Приведенные данные говорят, что наилучшие итоги должны по данным, которые выровнены на основании уровней исследуемого ряда динамики

Метод экспоненциального сглаживания

Экспоненциальное сглаживание – это выравнивание динамических рядов, весьма колеблются, цели стабильного прогнозирования По данному способу возможно дать обоснованные прогнозы на основе рядов динамики, имеют умеренный связь во времени, и обеспечить больше учета показателей, которые достигнуты за последние годы. Сущность метода оформляется в сглаживании временного ряда при помощи взвешенной текучей средней, в которые и веса подчиняются экспоненциальному закону.

Всякое сглажено значение рассчитано при помощи объединения прошлого текущего значения сглаженного значения и временного ряда. В данной ситуации текущие значения временного ряда разрешаются, учитывая константы, сглаживает.

Мы коротко рассмотрели м етод экстраполяции: методы, применение. Оставляйте свои комментарии или дополнения к материалу.

Источник