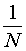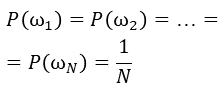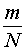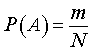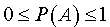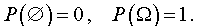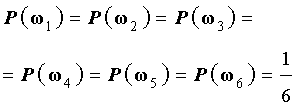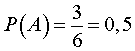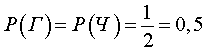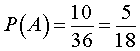Что такое элементарный исход в теории вероятностей
Что такое элементарный исход в теории вероятностей
уМЕДХЕФ РПНОЙФШ, ЮФП НЩ ЪБОЙНБЕНУС НБФЕНБФЙЛПК Й ЙНЕЕН ДЕМП ОЕ У ТЕБМШОПУФША, Б МЙЫШ У ЕЈ НБФЕНБФЙЮЕУЛПК НПДЕМША. нЩ Й ВХДЕН ЙЪХЮБФШ ФПМШЛП НБФЕНБФЙЮЕУЛЙЕ НПДЕМЙ, Б РТЙМПЦЕОЙЕ ЙИ Л ТЕБМШОПУФЙ ПУФБЧЙН ОБ ДПМА НБФЕНБФЙЮЕУЛПК Й РТБЛФЙЮЕУЛПК УФБФЙУФЙЛЙ.
рТЙНЕТЩ УПВЩФЙК: ЧЩРБМП ПДОП ЙМЙ ДЧБ ПЮЛБ; ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.
рТЙНЕТЩ УПВЩФЙК:
РТЙ РЕТЧПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
РТЙ ЧФПТПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
ОБ ЛПУФСИ ЧЩРБМП ПДЙОБЛПЧПЕ ЮЙУМП ПЮЛПЧ;
ОБ ПВЕЙИ ЛПУФСИ ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.
фБЛ, ЬЛУРЕТЙНЕОФЩ ЙЪ РТЙНЕТПЧ 1, 2 Й 4 (ОП ОЕ 3) РТЙЧПДСФ Л ДЙУЛТЕФОЩН РТПУФТБОУФЧБН ЬМЕНЕОФБТОЩИ ЙУИПДПЧ.
2. еУМЙ Й ОЕУПЧНЕУФОЩ, ФП ;
еУМЙ УПВЩФЙЕ УПУФПЙФ ЙЪ ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ФП ЧЕТПСФОПУФШ ЬФПЗП УПВЩФЙС ТБЧОСЕФУС ПФОПЫЕОЙА :
ОБЪЩЧБЕНПК ЛМБУУЙЮЕУЛЙН ПРТЕДЕМЕОЙЕН ЧЕТПСФОПУФЙ.
нЩ ЧЙДЙН ФЕРЕТШ, ЮФП РПДУЮЈФ ЧЕТПСФОПУФЙ Ч ЛМБУУЙЮЕУЛПК УИЕНЕ УЧПДЙФУС Л РПДУЮЈФХ ПВЭЕЗП ЮЙУМБ «ЫБОУПЧ» Й ЮЙУМБ ЫБОУПЧ, ВМБЗПРТЙСФУФЧХАЭЙИ ЛБЛПНХ-МЙВП УПВЩФЙА. юЙУМП ЫБОУПЧ УЮЙФБАФ У РПНПЭША ЖПТНХМ ЛПНВЙОБФПТЙЛЙ.
еУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБФШ, ФП УМЕДХЕФ ПВЯСЧЙФШ ДЧБ РПУМЕДОЙИ ЙУИПДБ ПДОЙН Й ФЕН ЦЕ ТЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ, Й РПМХЮЙФШ ОЕ ЮЕФЩТЕ, Б ФТЙ ЙУИПДБ:
рЕТЧЩЕ ДЧБ ЙУИПДБ ЙНЕАФ ЧЕТПСФОПУФЙ РП 1/4, Б РПУМЕДОЙК ЧЕТПСФОПУФШ 1/4+1/4=1/2.
тЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ОБВПТ ЙЪ ЫБТПЧ. нПЦОП ОЕ ХЮЙФЩЧБФШ ЙМЙ ХЮЙФЩЧБФШ РПТСДПЛ УМЕДПЧБОЙС ЫБТПЧ, ЧЕТПСФОПУФШ ОЕ ДПМЦОБ ЪБЧЙУЕФШ ПФ УРПУПВБ РПДУЮЈФБ.
чЩВПТ У ХЮЈФПН РПТСДЛБ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ ЕУФШ ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ЬМЕНЕОФПЧ ОБ НЕУФБИ: РП ФЕПТЕНЕ 2,
Классическое определение вероятности
Содержание
Случайный эксперимент. Множество элементарных исходов. Случайные события
Например, одним из случайных экспериментов, часто используемых в теории вероятностей, является подбрасывание игральной кости. Результатом этого случайного эксперимента будет количество выпавших очков.
Напомним, что игральная кость – это кубик из однородного материала, грани которого пронумерованы числами 1, 2, 3, 4, 5, 6 при помощи нанесенных на грани кубика точек.
Элементарные события часто называют элементарными исходами или, просто, исходами, а множество всех элементарных событий называют пространством элементарных событий, множеством элементарных исходов или пространством элементарных исходов.
Случайные события часто для простоты называют событиями.
Классическое определение вероятности
Если в результате случайного эксперимента может реализоваться один из нескольких равновозможных вариантов, то используют классическое определение вероятности.
Классическое определение вероятности является краеугольным камнем теории вероятностей и вводится в соответствии со следующей схемой.
Определяется множество элементарных событий (результаты случайного эксперимента).
В классическом определении вероятности в качестве множества элементарных событий Ω используют произвольное множество, состоящее из конечного числа элементов. Элементы множества Ω (элементарные события) обозначают
Вероятность каждого элементарного события полагают равной
Определяются случайные события.
Пустым множеством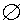 
называют множество, в котором нет ни одного элемента. Пустое множество содержится в любом множестве, то есть является подмножеством любого множества.
Определяется вероятность каждого случайного события.
Если A – случайное событие, то вероятность события A полагают равной числу
Вероятность случайного события A принято обозначать P (A).
Таким образом, справедливо равенство
причем, поскольку числитель в правой части формулы (1) не превосходит знаменателя, то вероятность любого случайного события A заключена в пределах
Примеры решения задач
составляют множество элементарных событий Ω :
Поскольку множество Ω состоит из 6 элементов, то вероятность каждого элементарного события равна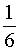 
:
Каждое случайное событие является подмножеством Ω и состоит из нескольких элементарных событий. Так, например, случайное событие
состоит из трех элементарных событий
В силу формулы (4) справедливо равенство
Элементарный исход
Пространство элементарных событий — множество Ω всех различных исходов случайного эксперимента.
Элемент этого множества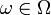 
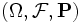
называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его элементов конечно или счётно. Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий Ω вместе с алгеброй событий 
и вероятностью 
образует тройку 
, которая называется вероятностным пространством.
См.также
Смотреть что такое «Элементарный исход» в других словарях:
Вероятностное пространство — У этого термина существуют и другие значения, см. Пространство. Вероятностное пространство понятие, введённое А. Н. Колмогоровым в 30 х годах XX века для формализации понятия вероятности, которое дало начало бурному развитию теории вероятностей… … Википедия
Случайный процесс — (случайная функция) в теории вероятностей семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты. Другое определение: Случайным называется процесс u(t), мгновенные значения… … Википедия
Пространство элементарных событий — Пространство элементарных событий множество всех различных исходов случайного эксперимента. Элемент этого множества называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его… … Википедия
Элементарное событие — В теории вероятностей элементарные события или события атомы это исходы случайного эксперимента, из которых в эксперименте происходит ровно один. Множество всех элементарных событий обычно обозначается Ω. Всякое подмножество множества Ω… … Википедия
Реализация случайной функции — Случайный процесс (случайная функция) в теории вероятностей семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или пространства. Содержание 1 Определение 2 Терминология 3 Классификация … Википедия
Эмпирическая функция распределения — Выборочная (эмпирическая) функция распределения в математической статистике это приближение теоретической функции распределения, построенное с помощью выборки из него. Определение Пусть выборка из распределения, задаваемого функцией распределения … Википедия
Эмпирическое распределение — Выборочная (эмпирическая) функция распределения в математической статистике это приближение теоретической функции распределения, построенное с помощью выборки из него. Определение Пусть выборка из распределения, задаваемого функцией распределения … Википедия
ТУБЕРКУЛЕЗ — ТУБЕРКУЛЕЗ. Содержание: I. Исторический очерк. 9 II. Возбудитель туберкулеза. 18 III. Патологическая анатомия. 34 IV. Статистика. 55 V. Социальное значение туберкулеза. 63 VІ.… … Большая медицинская энциклопедия