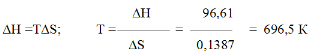Что такое энтальпия простыми словами в термодинамике
Основы теплотехники
Что такое энтальпия?
Попробуем уяснить физический смысл и суть понятия энтальпия, которое широко используется при расчетах и прогнозировании различных процессов в теплотехнике.
Уравнение первого закона термодинамики, выражающее закон сохранения энергии в термодинамических процессах, можно преобразовать к следующему виду:
Слово энтальпия в переводе с греческого означает «нагреваю».
Энтальпия тоже является параметром состояния, поскольку составляющие u и pv имеют для каждого состояния вполне определенные значения. Тогда первый закон термодинамики можно записать в виде:
Выражение (cv + T) в соответствии с уравнением Майера можно выразить через cp :
Значение энтальпии различных веществ в разных состояниях приведены в справочниках.
Энтальпия используется в вычислениях для определения разницы уровней энергии между двумя состояниями термодинамической системы.
Это бывает необходимо для настройки оборудования и определения коэффициента полезного действия процесса.
Понятие энтропии
В переводе с греческого слово «энтропия» означает превращение.
Этот параметр не имеет физического смысла и введен формально на основании математических построений для облегчения решения многих теплотехнических задач применительно к идеальному газу.
Произведение энтропии на изменение температуры системы характеризует изменение энергии системы. При этом даже если энергия системы будет изменяться, энтропия этой системы может оставаться неизменной. Очевидно, что при изотермических процессах (температура системы неизменна) составляющая энергии системы в которую входит энтропия равна нулю.
В общем случае изменение энергии термодинамической системы не является обязательным условием изменения энтропии этой системы.
Скачать теоретические вопросы к экзаменационным билетам
по учебной дисциплине «Основы гидравлики и теплотехники»
(в формате Word, размер файла 68 кБ)
Скачать рабочую программу
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):
Скачать календарно-тематический план
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):
Что такое энтальпия
Итак, что же такое энтальпия? Если говорить совсем упрощенно, энтальпия — это энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении. Когда я учился в университете, преподаватель помню, говорил нам, что энтальпию условно можно называть теплосодержанием, так как при постоянном давлении изменение энтальпии равно количеству теплоты, подведенной к системе.
И вообще, сам термин энтальпия составлен из древнегреческих слов — тепло и приставки — в. Это сочетание слов можно понимать как «нагревать». А впервые в термодинамику этот термин был введен ученым Д.Гиббсом. Ну это чтобы понятнее было, так как энтальпия, также кстати, как и энтропия, не может быть измерена непосредственно, как например давление или температура. Энтальпия определяется только расчетным путем. То есть, образно говоря, ее нельзя «потрогать», «пощупать».
Рассмотрим более подробно. Значение энтальпии вещества определяется из выражения:
где u – внутренняя энергия; p, u – давление и удельный объем рабочего тела в том же состоянии, для которого взято значение внутренней энергии.
То есть, можно сказать, что энтальпия любой термодинамической системы представляет собой сумму внутренней энергии системы и потенциальной энергии источника внешнего давления.
Энтальпия находится как сумма величин, которые определяются состоянием вещества, представляет собой функцию состояния и измеряется в Дж/кг. Чаще энтальпия во внесистемной системе измерений измеряется в ккал/кг. Энтальпия является одной из вспомогательных функций, использование которой позволяет значительно упрощать термодинамические расчеты. Так например, огромное количество процессов подвода теплоты в теплоэнергетике (в паровых котлах, камерах сгорания газовых турбин и реактивных двигателей, теплообменных аппаратах) осуществляется при постоянном давлении. По этой причине в таблицах термодинамических свойств обычно приводятся значения энтальпии.
В технической термодинамике пользуются значениями энтальпии, которые отсчитываются от условно принятого нуля. Абсолютные значения этих величин весьма трудно определить, так как для этого необходимо учесть все составляющие внутренней энергии вещества при изменении его состояния от 0 К. В таблицах и на диаграммах часто приводятся значения i и s, которые отсчитываются от 0 °С.
В заключение можно сказать, что энтальпия аналогично внутренней энергии и другим термодинамическим параметрам имеет вполне определенное значение для каждого состояния, то есть является функцией состояния рабочего тела.
Энтальпия — что это такое простыми словами
Про энтальпию на простом языке
При работе с какими-либо расчётами, вычислениями и выполнении прогноза разнообразных явлений, связанных с теплотехникой, каждый сталкивается с понятием энтальпия. Но для людей, специальность которых не касается теплоэнергетики или которые лишь поверхностно сталкиваются с подобными терминами, слово «энтальпия» будет наводить страх и ужас. Итак, давайте разберёмся, действительно ли всё так страшно и непонятно?
Если попытаться сказать совсем просто, под термином энтальпия понимается энергия, которая доступна для преобразования в теплоту при некотором постоянном давлении. Понятие энтальпия в переводе с греческого значит «нагреваю». То есть формулу, содержащую элементарную сумму внутренней энергии и произведенную работу, называют энтальпией. Эта величина обозначается буквой i.
Если записать вышесказанное физическими величинами, преобразовать и вывести формулу, то получится i = u + pv (где u – внутренняя энергия; p, u – давление и удельный объем рабочего тела в том же состоянии, для которого взято значение внутренней энергии). Энтальпия — аддитивная функция, т. е. энтальпия всей системы равна сумме всех составляющих её частей.
Термин «энтальпия» сложен и многогранен.
Но если постараться в нём разобраться, то всё пойдёт очень просто и понятно.
Ну, что же, механизм работы понятен. Вам лишь нужно внимательно читать и вникать. С термином «Энтальпии» мы уже разобрались, также привели и его формулу. Но тут же возникает ещё один вопрос: откуда взялась эта формула и почему энтропия связана, к примеру, с внутренней энергией и давлением?
Суть и смысл
Для того, чтобы попытаться выяснить физический смысл понятия «энтальпия» нужно знать первый закон термодинамики:
энергия не исчезает в никуда и не возникает из ничего, а лишь переходит из одного вида в другой в одинаковых количествах. Таким примером может служить переход теплоты (тепловой энергии) в механическую энергию, и наоборот.
Уравнение первого закона термодинамики нам нужно преобразить в вид dq = du + pdv = du + pdv + vdp – vdp = d(u + pv) – vdp. Отсюда мы видим выражение (u + pv). Именно это выражение и называется энтальпией (полная формула приводилась выше).
Энтальпия также является величиной состояния, потому что составляющие u (напряжение) и p (давление), v (удельный объём) имеют для каждой величины определенные значения. Зная это, первый закон термодинамики возможно переписать в виде: dq = di – vdp.
В технической термодинамике используются значения энтальпии, которые высчитываются от условно принятого нуля. Все абсолютные значения этих величин весьма трудно определить, так как для этого необходимо учесть все составляющие внутренней энергии вещества при изменении его состояния от О к К.
Формулу и значения энтальпии привёл в 1909 г. учёный Г.Камерлинг-Оннесом.
В выражении i — удельная энтальпия, для всей массы тела полная энтальпия обозначается буквой I, по всемирной системе единиц энтальпия измеряется в Джоулях на килограмм и рассчитывается как:
Функции
Энтальпия («Э») является одной из вспомогательных функций, благодаря использованию которой можно значительно упростить термодинамический расчёт. Так например, огромное количество процессов подвода теплоты в теплоэнергетике (в паровых котлах или камере сгорания газовых турбин и реактивных двигателей, а также в теплообменных аппаратах) осуществляют при постоянном давлении. По этой причине в таблицах термодинамических свойств обычно приводят значения энтальпии.
Условие сохранения энтальпии лежит, в частности, в основе теории Джоуля — Томсона. Или эффекта, нашедшего важное практическое применение при сжижении газов. Таким образом, энтальпия есть полная энергия расширенной системы, представляющая сумму внутренней энергии и внешней – потенциальной энергии давления. Как любой параметр состояния, энтальпия может быть определена любой парой независимых параметров состояния.
Также, исходя из приведённых выше формул, можно сказать: «Э» химической реакции равна сумме энтальпий сгорания исходных веществ за вычетом суммы энтальпий сгорания продуктов реакции.
В общем случае изменение энергии термодинамической системы не является необходимым условием для изменения энтропии этой системы.
Итак, вот мы и разобрали понятие «энтальпии». Стоит отметить, что «Э» неразрывно связана с энтропией, о которой вы также можете прочесть позже.
Энергетика химических процессов. Энтальпия, законы термодинамики
» data-shape=»round» data-use-links data-color-scheme=»normal» data-direction=»horizontal» data-services=»messenger,vkontakte,facebook,odnoklassniki,telegram,twitter,viber,whatsapp,moimir,lj,blogger»>
Энергетика химических процессов
Науку о взаимных превращениях различных видов энергии называют термодинамикой. Термодинамика устанавливает законы этих превращений, а также направление самопроизвольного течения различных процессов в данных условиях.
5.1. Общие понятия. При протекании химических реакций изменяется энергетическое состояние системы, в которой идет эта реакция. Состояние системы характеризуется термодинамическими параметрами (р, Т, с и др.). При изменении параметров меняется и состояние системы. В термодинамике свойства системы рассматриваются при ее равновесном состоянии. Термодинамическое состояние системы называют равновесным в том случае, когда его термодинамические параметры одинаковы во всех точках системы и не изменяются самопроизвольно (без затраты работы) во времени. Термодинамика изучает переходы системы из одного состояния в другое. Но переходы должны осуществляться при термодинамическом равновесии с окружающей средой, т.е. очень медленно, а в идеале — бесконечно медленно. При этом могут изменяться все параметры состояния системы, либо некоторые параметры остаются без изменения. Если процессы перехода системы происходят при постоянстве каких-то параметров системы, то они называются:
а) изобарическими (р = const);
б) изохорическими (Т= const);
в) изотермическими (Т = const);
г) изобарно-изотермическими (р,T – const) и т.д.
Термодинамика изучает возможность или невозможность самопроизвольного перехода системы из одного состояния в другое и энергетические эффекты этих переходов. Скорость и механизм процессов перехода — это области химической кинетики.
5.2. Внутренняя энергия. Первый закон термодинамики. При химических реакциях происходят глубокие качественные изменения в системе, рвутся связи в исходных веществах и возникают новые связи в конечных продуктах. Эти изменения сопровождаются поглощением или выделением энергии. В большинстве случаев этой энергией является теплота. Раздел термодинамики, изучающий тепловые эффекты химических реакций, называют термохимией. Реакции, которые сопровождаются выделением теплоты, называют экзотермическими, а те, которые сопровождаются поглощением теплоты, — эндотермическими. Теплота реакции является, таким образом, мерой изменения свойств системы, и знание ее может иметь большое значение при определении условий протекания той или иной реакции.
При любом процессе соблюдается закон сохранения энергии как проявление более общего закона природы — закона сохранения материи. Теплота Q, поглощенная системой, идет на изменение ее внутренней энергии и на совершение работы А:
Количественное соотношение между изменением внутренней энергии, теплотой и работой устанавливает первый закон термодинамики:
Уравнение означает, что теплота, подведенная к системе, расходуется на приращение внутренней энергии системы и на работу системы над окружающей средой.
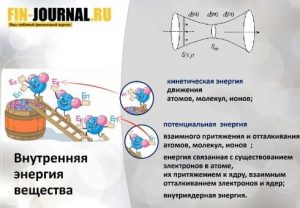
Внутренняя энергия системы U — это общий ее запас, включающий энергию поступательного и вращательного движений молекул, энергию внутримолекулярных колебаний атомов и атомных групп, энергию движения электронов, внутриядерную энергию и т.д. Внутренняя энергия — полная энергия системы без потенциальной энергии, обусловленной положением системы в пространстве, и без кинетической энергии системы как целого. Абсолютное значение внутренней энергии U веществ неизвестно, так как нельзя привести систему в состояние, лишенное энергии. Внутренняя энергия, как и любой вид энергии, является функцией состояния, т.е. ее изменение однозначно определяется начальным и конечным состояниями системы и не зависит от пути перехода, по которому протекает процесс:
где: U – изменение внутренней энергии системы при переходе из начального состояния U1 в конечное U2. Если U2 > U1, то U> 0.
Если U2 0 (Н2 > Н1). В дальнейшем тепловые эффекты всюду выражаются через H.
5.4. Термохимические расчеты. Термохимические расчеты основаны на законе Гесса, позволяющее рассчитать энтальпию химической реакции: тепловой эффект реакции зависит только от природы и физического состояния исходных веществ и конечных продуктов, но не зависит от пути перехода.
Часто в термохимических расчетах применяют следствие из закона Гесса: тепловой эффект реакции (Нx.p.) равен сумме теплот образования Нобр продуктов реакции за вычетом суммы теплот образования исходных веществ с учетом коэффициентов перед формулами этих веществ в уравнении реакции:
Пример 1. При взаимодействии кристаллов хлорида фосфора (V) с парами воды образуется жидкий РОС13 и хлороводород. Реакция сопровождается выделением 111,4 кДж теплоты. Напишите термохимическое уравнение этой реакции.
Решение. Уравнения реакций, в которых около символов химических соединений указываются их агрегатные состояния или кристаллическая модификация, а также числовое значение тепловых эффектов, называют термохимическими. В термохимических уравнениях, если это специально не оговорено, указываются значения тепловых эффектов при постоянном давлении Qp, равные изменению энтальпии системы Н. Значение Н приводят обычно в правой части уравнения, отделяя его запятой или точкой с запятой. Приняты следующие сокращенные обозначения агрегатного состояния вещества: г — газообразное, ж — жидкое, к — кристаллическое. Эти символы опускаются, если агрегатное состояние веществ очевидно.
Вычислите теплоту образования этана, если известны теплоты образования СO2(г) и Н2O(ж) (см. табл. 15).
Решение. Теплотой образования (энтальпией) данного соединения называют тепловой эффект реакции образования 1 моль этого соединения из простых веществ, взятых в их устойчивом состоянии при данных условиях.
Обычно теплоту образования относят к стандартному состоянию, т.е. 25° С (298 К) и 1,01310 5 Па и обозначают через.Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид
исходя из следующих данных:
На основании закона Гесса с термохимическими уравнениями можно оперировать так же, как и с алгебраическими. Для получения искомого результата следует уравнение (б) умножить на 2, уравнение (в) — на 3, а затем сумму этих уравнений вычитают из уравнения (а):
∆H =-1559,87-2(-393,51)-3(-285,84)= +84,67 кДж;
К тому же результату придем, если для решения задачи применить вывод из закона Гесса:
Учитывая, что теплоты образования простых веществ условно приняты равными нулю
Пример 3. Реакция горения этилового спирта выражается термохимическим уравнением
Вычислите тепловой эффект реакции, если известно, что молярная теплота парообразования С2Н5OН(ж) равна +42,36 кДж, а теплоты образования С2Н5OН(г), СO2(г), Н2O(ж) см. табл. 15.
Решение. Для определения Н реакции необходимо знать теплоту образования С2Н5OН(ж). Последнюю находим из данных:
Вычисляем H реакции, применяя следствие из закона Гесса:
5.5. Химическое сродство. Энтропия химических реакций. Энергия Гиббса. Самопроизвольно могут протекать реакции, сопровождающиеся не только выделением, но и поглощением теплоты.
Реакция, идущая при данной температуре с выделением теплоты, при другой температуре проходит с поглощением теплоты. Здесь проявляется диалектический закон единства и борьбы противоположностей. С одной стороны, система стремится к упорядочению (агрегации), к уменьшению Н; с другой стороны, система стремится к беспорядку (дезагрегации). Первая тенденция растет с понижением, а вторая — с повышением температуры. Тенденцию к беспорядку характеризует величина, которую называют энтропией.
Энтропия S, так же как внутренняя энергия U, энтальпия Н, объем V и др., является свойством вещества, пропорциональным его количеству. S, U, H, V обладают аддитивными свойствами, т.е. при соприкосновении системы суммируются. Энтропия отражает движение частиц вещества и является мерой неупорядоченности системы. Она возрастает с увеличением движения частиц: при нагревании, испарении, плавлении, расширении газа, при ослаблении или разрыве связей между атомами и т.п. Процессы, связанные с упорядоченностью системы: конденсация, кристаллизация, сжатие, упрочнение связей, полимеризация и т.п.— ведут к уменьшению энтропии. Энтропия является функцией состояния, т.е. ее изменение зависит только от начального (S1) и конечного (S2) состояний и не зависит от пути процесса:
Так как энтропия увеличивается с повышением температуры, то можно считать, что мера беспорядка равна TS. Энтропия выражается в Дж/(моль.К).
Таким образом, движущая сила процесса складывается из двух сил: стремления к упорядочению (Н) и стремления к беспорядку (TS). При р = const и Т = const общую движущую силу процесса, которую обозначают G, можно найти из соотношения
где: величина G называется изобарно-изотермическим потенциалом или энергией Гиббса.
Мерой химического сродства является убыль энергии Гиббса (G), которая зависит от природы вещества, его количества и температуры.
Энергия Гиббса является функцией состояния, поэтому
Самопроизвольно протекающие процессы идут в сторону уменьшения потенциала и, в частности, в сторону уменьшения G. Если G 0, процесс самопроизвольно проходить не может. Чем меньше G, тем сильнее стремление к протеканию данного процесса и тем дальше он от состояния равновесия, при котором G = 0 и H= TS.
Из соотношения G = H – TS видно, что самопроизвольно могут протекать и процессы, для которых H>0 (эндотермические). Это возможно, когда S>0, но |TS| > |H| и тогда G 0.
5.6. Второй и третий законы термодинамики. Для систем, которые не обмениваются с окружающей средой ни энергией, ни веществом (изолированные системы), второй закон термодинамики имеет следующую формулировку: в изолированных системах самопроизвольно идут только такие процессы, которые сопровождаются возрастанием энтропии: AS > 0.
Второй закон термодинамики имеет статистический характер, т.е.
справедлив лишь для систем, состоящих из очень большого числа
частиц.
Однако, если в системе протекает химическая реакция, то система обменивается энергией с окружающей средой, т.е. не является изолированной. Химические реакции обычно сопровождаются изменением как энтропии, так и энтальпии.
В отличие от других термодинамических функций, можно определить не только изменение, но абсолютное значение энтропии. Это вытекает из высказанного в 1911 г. М. Планком постулата, согласно которому «при абсолютном нуле энтропия идеального кристалла равна нулю». Этот постулат получил название третьего закона термодинамики.
Пример 1. В каком состоянии энтропия 1 моль вещества больше при одинаковой температуре: в кристаллическом или парообразном?
Решение. Энтропия есть мера неупорядоченности состояния вещества. В кристалле частицы (атомы, ионы) расположены упорядоченно и могут находиться лишь в определенных точках пространства, а для газа таких ограничений нет. Объем 1 моль газа гораздо больше объема 1 моль кристаллического вещества; возможность хаотичного движения молекул газа больше. А так как энтропию можно рассматривать как количественную меру хаотичности атомно-молекулярной структуры вещества, то энтропия 1 моль паров вещества больше энтропии 1 моль его кристаллов при одинаковой температуре.
Пример 2. Прямая или обратная реакция будет протекать при стандартных условиях в системе
Решение. ВычислимΔG 0 298 прямой реакции. Значения ΔG 0 298соответствующих веществ приведены в табл. 16. Зная, что ΔG есть функция состояния и что ΔG для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, находим ΔG 0 298процесса:
∆G 0 298 = 2 (-137,27) +2 (0) – (-50,79-394,38) = +170,63 кДж
То, что ΔG 0 298> 0, указывает на невозможность самопроизвольного протекания прямой реакции при Т = 298К и давлении взятых газов равном 1,013 ∙ 10 5 Па (760 мм рт. ст. = 1 атм).
Стандартная энергия Гиббса образования ΔG 0 298некоторых веществ
| Вещество | Состояние | ΔG 0 298, кДж/моль | Вещество | Состояние | ΔG 0 298, кДж/моль |
| ВаСО3 | к | -1138,8 | FeO | к | -244,3 |
| СаСО3 | к | -1128,75 | Н2О | ж | -237,19 |
| Fе3O4 | к | -1014,2 | Н2O | г | -228,59 |
| ВеСО3 | к | -944,75 | PbO2 | к | -219,0 |
| СаО | к | -604,2 | СО | г | -137,27 |
| ВеО | к | -581,61 | СН4 | г | -50,79 |
| NaF | к | -541,0 | NO2 | г | +51,84 |
| ВаО | к | -528,4 | NO | г | +86,69 |
| СО2 | г | -394,38 | C2H2 | г | +209,20 |
| NaCl | к | -384,03 | |||
| ZnO | к | -318,2 |
Стандартные абсолютные энтропии ΔS 0 298 некоторых веществ
| Вещество | Состояние | ΔS 0 298, Дж/(моль.К) | вещество | Состояние | ΔS 0 298,Дж/(моль.К) |
| С | Алмаз | 2,44 | Н2O | г | 188,72 |
| С | Графит | 5,69 | N2 | г | 191,49 |
| Fe | к | 27,2 | NН3 | г | 192,50 |
| Ti | к | 30,7 | СО | г | 197,91 |
| S | Ромб | 31,9 | с2H2 | г | 200,82 |
| TiO2 | к | 50,3 | O2 | г | 205,03 |
| FeO | к | 54,0 | H2S | г | 205,64 |
| H2O | ж | 69,94 | NO | г | 210,20 |
| Fе2О3 | к | 89,96 | CO2 | г | 213,65 |
| NH4C1 | к | 94,5 | C2H4 | г | 219,45 |
| СН3ОН | ж | 126,8 | Cl2 | г | 222,95 |
| Н2 | г | 130,59 | NO2 | г | 240,46 |
| Fе3O4 | к | 146,4 | РС13 | г | 311,66 |
| СН4 | г | 186,19 | PCl5 | г | 352,71 |
| НС1 | г | 186,68 |
Пример 3. На основании стандартных теплот образования (см. табл. 15) и абсолютных стандартных энтропий веществ (табл.17) вычислите ΔS 0 298 реакции, протекающей по уравнению
Решение. ∆G 0 = ∆H 0 – TS 0 ; ∆H и ∆S – функции состояния, поэтому
∆Н 0 х.р.=∑ ∆Н 0 прод – ∑ ∆Н 0 исх ; ∆S 0 x.p.= ∑S 0 прод – ∑ S 0 исх
∆Н 0 х.р.=(-393,51+0) – (110,52 – 285,84) = +2,85 кДж
∆S 0 x.p.=(213,65+130,59)-(197,91+69,94) = +76,39 = 0,07639 кДж/(моль∙К);
∆G 0 = +2,85 – 298 ∙ 0,07639 = – 19,91 кДж
Пример 4. Реакция восстановления Fе2О3 водородом протекает по уравнению
Возможна ли эта реакция при стандартных условиях, если изменение энтропии S=0,1387 кДж/(мольК)? При какой температуре начнется восстановление Fе2О3?
Решение. Вычисляем ∆G 0 реакции:
∆G = ∆Н-Т∆S = 96,61 – 298 ∙ 0,1387 = +55,28 кДж
Так как ∆G > 0, то реакция при стандартных условиях невозможна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру, при которой∆G=0:
Следовательно, при температуре 696,5 К начнется реакция восстановления Fе2О3 Иногда эту температуру называют температурой начала реакции.
Возможна ли реакция восстановления Fе2О3 углеродом при 500 и 1000 К?
Решение. ∆H 0 xp и ∆S 0 xp находим из соотношений (1) и (2) (см. разделы «Энергетика химических процессов. Термохимические расчеты» и «Химическое сродство»):
∆S 0 x.p.=(2 ∙ 27,2+3 ∙ 197,91) – (89,96+3 ∙ 5,69) = 541,1 Дж/(моль ∙ К)
Энергию Гиббса при соответствующих температурах находим из соотношения