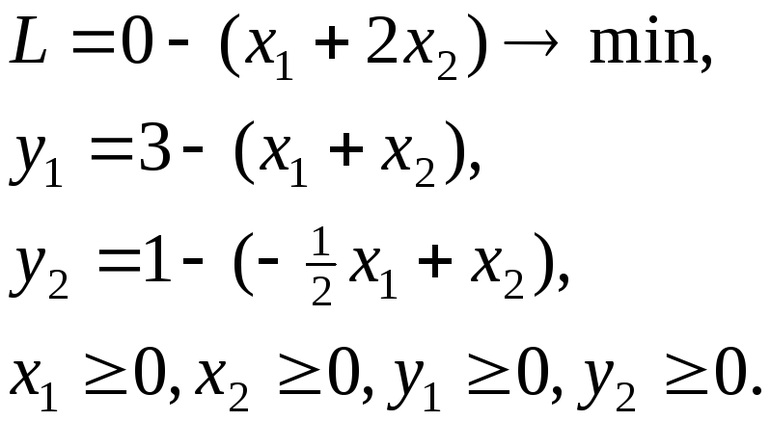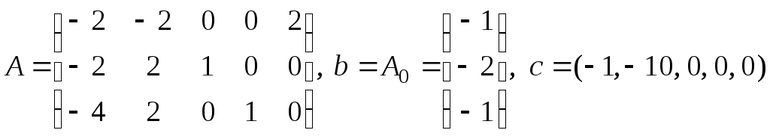Что такое опорный план в симплекс методе
Лекция 6
Алгоритм симплекс метода
Симплекс метод (метод последовательного улучшения плана)
Метод предназначен для решения общей задачи линейного программирования.
Пусть имеем следующую задачу:
с системой ограничений следующего вида:
Целевую функцию можно выразить через небазисные переменные:
Вектор с такими компонентами представляет собой угловую точку многогранника решений (допустимую) при условии, что (опорный план).
Теперь необходимо перейти к другой угловой точке с меньшим значением целевой функции. Для этого следует выбрать некоторую небазисную переменную и некоторую базисную так, чтобы после того, как мы “поменяем их местами”, значение целевой функции уменьшилось. Такой направленный перебор в конце концов приведет нас к решению задачи.
Пример 1.
Выберем в качестве базисных следующие переменные < x1, x2, x3> и разрешим систему относительно этих переменных. Система ограничений примет следующий вид:
Значение целевой функции можно уменьшить за счет увеличения x5. При увеличении x5 величина x1 также увеличивается, а x2 и x3 – уменьшаются. Причем величина x2 раньше может стать отрицательной. Поэтому, вводя в базис переменную x5, одновременно x2 исключаем из базиса. В результате после очевидных преобразований получим следующие выражения для новой системы базисных переменных и целевой функции:
Целевую функцию можно уменьшить за счет увеличения x4. Увеличение x4 приводит к уменьшению только x3. Поэтому вводим в базис переменную x4, а x3 исключаем из базиса. В результате получим следующие выражения для новой системы базисных переменных и целевой функции:
Пример 2.
Пусть имеем задачу
Теперь вводим в базис переменную x1, a x4 исключаем из базиса. В результате получим следующие выражения для базисных переменных и целевой функции:
Теперь можно заметить, что при увеличении x2 значения переменных x1 и x3 также возрастают, то есть при в допустимой области (задача не имеет решения).
Замечание
В процессе поиска допустимого плана может быть выявлена противоречивость системы ограничений.
Алгоритм симплекс метода
Проиллюстрируем алгоритм на рассмотренном ранее примере:
В случае базисных переменных < x1, x2, x3>начальная симплексная таблица для данного примера будет выглядеть следующим образом:
| — x4 | — x5 | 1 | |
| x1= | 1 | -2 | 1 |
| x2= | -2 | 1 | 2 |
| x3= | 3 | 1 | 3 |
| = | -1 | 1 | 0 |
Она уже соответствует опорному плану (столбец свободных членов).
Построение оптимального плана.
Выбор разрешающего элемента. Если при поиске минимума в строке целевой функции есть коэффициенты больше нуля, то выбираем столбец с положительным коэффициентом в строке целевой функции в качестве разрешающего. Пусть это столбец с номером l.
Для выбора разрешающей строки (разрешающего элемента) среди положительных коэффициентов разрешающего столбца выбираем тот (строку), для которого отношение коэффициента в столбце свободных членов к коэффициенту в разрешающем столбце минимально:
arl – разрешающий (направляющий) элемент, строка r – разрешающая.
Для перехода к следующей симплексной таблице (следующему опорному плану с меньшим значением целевой функции) делается шаг модифицированного жорданова исключения с разрешающим элементом arl.
Если в разрешающем столбце нет положительных коэффициентов, то целевая функция неограничена снизу (при максимизации – неограничена сверху).
Шаг модифицированного жорданова исключения над симплексной таблицей. На месте разрешающего элемента ставится 1 и делится на разрешающий элемент.
Остальные элементы разрешающего столбца меняют знак на противоположный и делятся на разрешающий элемент.
Остальные элементы разрешающей строки делятся на разрешающий элемент.
Построение опорного плана.
Пусть необходимо решить задачу:
Введем дополнительные переменные, чтобы преобразовать ограничения-неравенства к равенствам. В ограничениях-равенствах дополнительные переменные должны быть нулевыми. Тогда система ограничений принимает вид:
В качестве базисных переменных будем брать систему дополнительно введенных переменных. Тогда симплексная таблица для преобразованной задачи будет иметь следующий вид:
| — x1 | — x2 | …. | — xs | .… | — xn | 1 | |
| 0 | a1,1 | a1,2 | …. | a1,s | …. | a1,n | b1 |
| …. | …. | …. | …. | …. | …. | …. | …. |
| 0 | am,1 | am,2 | …. | am,s | …. | am,n | bm |
| xm+1 | am+1,1 | am+1,2 | …. | am+1,s | …. | am+1,n | bm+1 |
| …. | …. | …. | …. | …. | …. | …. | …. |
| xm+p | am+p,1 | am+p,2 | …. | am+p,s | …. | am+p,n | bm+p |
| — c1 | — c2 | …. | — cs | …. | — cn | 0 |
Вырожденность в задачах линейного программирования
Если задача линейного программирования оказывается вырожденной, то при плохом выборе вектора условий, выводимого из базиса, может возникнуть бесконечное движение по базисам одного и того же опорного плана. Так называемое, явление зацикливания. Хотя в практических задачах линейного программирования зацикливание явление крайне редкое, возможность его не исключена.
Один из приемов борьбы с вырожденностью состоит в преобразовании задачи путем «незначительного» изменения вектора правых частей системы ограничений на величины εi, таким образом, чтобы задача стала невырожденной, и, в то же время, чтобы это изменение не повлияло реально на оптимальный план задачи.
Чаще реализуемые алгоритмы включают в себя некоторые простые правила, снижающие вероятность возникновения зацикливания или его преодоления.
Практически правилом надо пользоваться, если зацикливание уже обнаружено.
Понятие и алгоритм
Под симплексным методом понимается последовательный переход от одного базисного нахождения системы решений к другому. Эта перестановка повторяется до тех пор, пока переменная величина цели не достигнет своего наибольшего или наименьшего значения. Такой подход является универсальным, его можно использовать для решения любой задачи последовательного программирования.
Метод был разработан в 1947 году математиком из США Бернардом Данцигом. Предложенный способ оказался весьма эффективным для решения задач, связанных с оптимизацией использования ограниченных ресурсов. То есть он позволяет оценить и откорректировать параметры системы, а также получить качественные аналитические результаты.
Существует два подхода решения задачи:
Первый можно использовать для оптимизационного решения двухмерных задач. Например, существует два производственных цикла по сборке ящиков. Выпуск товара характеризуется ограничением в поставках древесины и временем формовки изделия. Для одного необходимо 30 досок, а для другого — 40. Поставщики доставляют в неделю 2 тыс. единиц материала. Первый ящик собирается за 15 минут, а второй — за 30. Нужно определить, какое количество ящиков необходимо производить за неделю на первом конвейере и на втором. При этом первое изделие приносит 10 рублей прибыли, а второе — пять. Время изготовление ограничено 160 часами.
Решение заключается в принятии за Х1 и Х2 количество выпущенных ящиков. Затем — в нахождении максимальной еженедельной прибыли и описании процесса ограничения в виде уравнения.
Это типовая двухмерная задача, условия неотрицательности которой определяются границами прямых: 30*Х1 + 4 0*Х 2 ≤ 2000 (для досок) и 20*Х 1 ≤ 50*Х 2 = 1600 (для сборки). Отложив по оси ординат Х1, а Х2 по абсцисс, и указав на них точки соответствующие уравнениям, можно будет подобрать оптимальное решение для использования сырья и времени.
Графический метод удобно применять для двухмерных задач, но его невозможно использовать при решениях, связанных с размерностью, превышающей три. При этом во всех алгоритмах оптимальный результат принимается допустимым базисному. Симплекс-метод же является вычислительной процедурой, использующей принятое положение, описываемое в алгебраической форме.
Симплекс-метод при базисном решении
Впервые способ был изложен Данцигом в книге «Линейное программирование, его обобщения и применения», изданной на русском языке в 1966 году. Эта теория основывалась на вычислительной процедуре и представлялась в виде стандартных алгебраических форм. Основное направление метода заключается в указании способа нахождения опорного решения, переходе к другому, более оптимальному расчёту и определении критериев, позволяющих остановить перебор опорных вариантов.
Алгоритм решения задачи линейного программирования симплекс методом следующий:
Другими словами, указывается оптимальное опорное решение, способ перехода от одного нахождения ответа к другому, варианты улучшения расчётов. После нахождения первоначального решения с «единичным базисом» вычисляется оценка разложения векторов по базису и заполняется симплексная таблица.
В тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи, используют метод с искусственным базисом. Это симплекс-метод с так называемой М-задачей (ММЭ), решаемый способом добавления к левой части системы уравнений искусственных единичных векторов. При этом новая матрица должна содержать группу единичных линейно-независимых векторов.
Двухфазный способ
Двойственный метод используется при анализе задач линейного программирования, записанного в форме основной задачи. При этом среди векторов, m уравнений, составленных из коэффициентов, должны быть единичные. Такой метод можно использовать, когда свободные члены уравнений являются любыми числами.
Например, существует ограниченность, описываемая функцией:
F = C 1 X 1+ C 2 X 2+…+ CnXn. Используется условие, что Х1Р1+Х2Р2+…+Х(m +1) P (m +1)+ +… XnPn = Р0, где Х j больше либо равно 0 (j =1, n). Принимается, что среди чисел bi (i =1, m) имеются отрицательные.
Решением будет выражение: х= (b1; b2;…; bm ;0;…;0), однако этот ответ не будет разрешать задание, так как к нему могут относиться и отрицательные числа. Так как векторы Р1, Р2… Рм единичные, то каждый из них можно описать линейной областью, состоящей из них же. При этом коэффициентами разложения векторов Рj по области будут числа: Xij = aij (i =1, m; j =1, n) по модулю.
Выражение х= ( b1; b2;…; bm ;0;…;0) определяется базисом. Называют его псевдоплан. Считается, что если дельта j больше либо равна нулю, то для любого: j ( j =1, n ) по модулю. В то же время если в псевдоплане с находимым базисом существует хотя бы одно отрицательное число, то тогда задача вообще не будет иметь планов. Но когда для этих отрицательных чисел верно, что аij меньше нуля, то можно будет перейти к новому псевдоплану.
Объяснение псевдоплана помогает построить алгоритм двойственного метода. Если взять за основу х = (b1; b2;…; bm ;0;…;0) и представить это выражение псевдопланом, то, учитывая исходные данные, можно составить симплекс-таблицу. В ней часть элементов будет отрицательная. Так как дельта j должна быть больше либо равна нулю, то при отсутствии таких чисел в таблице уже будет записан оптимальный план. В обратном случае выбирается по модулю наибольшее из чисел с минусом.
Принцип решения задачи включает следующее:
Если анализ оптимален, считается, что найдено верное решение. В другом случае устанавливается неразрешимость задачи либо составляется новый псевдоплан. Делается это в результате пересчёта табличных данных, например, методом Жордана-Гаусса.
Пример задачи
Использование метода линейного программирования распространено в решениях транспортных задач. Он помогает в целевых расчётах и нужен для минимизации затрат в условиях ограниченной грузоподъёмности и времени обслуживания заказчиков.
Задачи линейного программирования (ЗЛП) позволяют выбрать оптимальную загрузку при перемещении какого-либо товара из одних мест в другие. Во вводных данных указывается число пунктов отправления (м) и количество мест назначения (n). Первые обозначаются как А1, А2…Ам, а вторые – В1, В2…Вn. За аi принимается объём продукции на складе, а bi – потребность. Затраты на перевозку с i пункта в j обозначаются Сij.
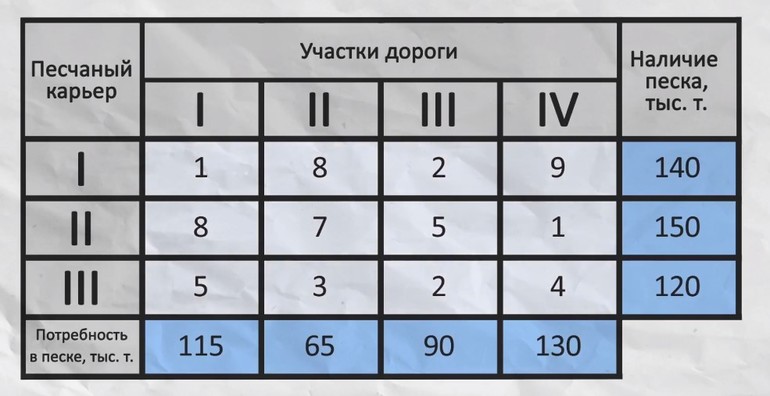
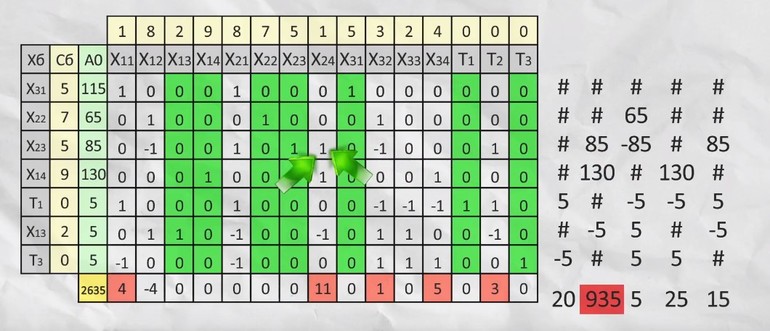
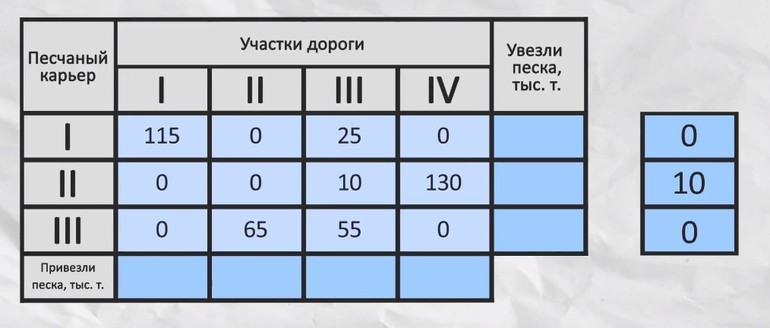
Главная задача — составить план таким образом, чтобы общая стоимость была минимальна. Пусть дано четыре песчаных карьера, с которых необходимо поставить песок на четыре склада. При этом осуществляться перевозки должны за определённую стоимость. Составляем таблицу.
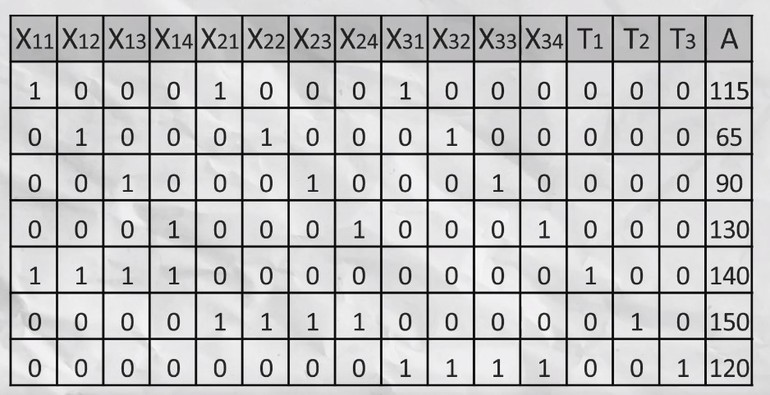
Записываем уравнение ограничения. Сумма всего перевезённого песка с первого карьера должна быть меньше или равна 140. Поэтому можно записать: x11+x12+x12+x14+T1 = 140, где Т1 переменная для хранения остатка. Сумма ограничений будет записана как х11+х21+х31 =115. Аналогичные уравнения составляют и для оставшихся карьеров.
В последней строчке прямоугольника проставляют сумму произведений Сб на этот столбец и вычитают значение суммы перемножения Сб с А0. Делают дополнительное вычисление. Для каждой строки А0 делят на выделенное число, ищут наименьший результат и умножают его на положительные числа из последней строки.
Наибольшее число определяется пересечением ранее выбранных значений, на базе которых создают новый базис. После в соответствии с единичными базисами меняют Сб и Хб. Операцию повторяют до тех пор, пока не исчезнут все положительные числа из последней строки. Заполняют новую таблицу.
Расчёт в Excel
Для включения пакета анализа в программе необходимо перейти в раздел «Параметры» и выбрать строчку «Перейти». В новом окне найти строчку «Пакет анализа», кликнуть по ней и нажать кнопку ОК.
Затем понадобится загрузить и открыть шаблон для проверки в Excel. Используя манипулятор типа «мышь» или клавиатуру, выбрать ячейку G4 и выполнить команду «Сервис/Поиск решения». Далее указать исходные данные, а после нажать кнопку «Выполнить».
Полученное решение можно представить в форме отчёта, содержащего:
Онлайн-сервис для чайников
Метод решения относится к высшей математике, поэтому в нём довольно трудно разобраться даже подготовленному человеку, не говоря уже о чайнике. Существует некоторое количество сайтов с подробным онлайн-решением методом симплекса. На таких сервисах предлагается ввести количество переменных и строк (ограничений). А далее просто заполнить симплекс-таблицу и нажать расчёт. Причём при необходимости вводимые данные можно править, тем самым видеть, как изменяется результат от изменения исходной информации.
Удобным является ещё и то, что обычно на сайтах предлагается создать шаблон решения в Excel или Maple. Решаться любая задача будет почти мгновенно. Подробно можно выполнить расчёт онлайн-калькулятор по методу симплекса на следующих сайтах:
Выполнить расчёт с помощью онлайн-сервисов сможет любой. При этом вероятность ошибки в ответе стремится к нулю. Тем более что для решения задачи даже необязательно знать принцип симплекс-метода.
Транспортная задача линейного программирования
Транспортная задача линейного программирования
Транспортная задача линейного программирования относится к перечню классических задач, решаемых в практике деятельности людей. Эта задача методами классической математики не решается. В задаче необходимо отыскивать экстремум целевой функции. В задаче целевая функция – линейная. Ограничения на переменные (их может быть очень много) описываются также линейными зависимостями. Казалось бы чего проще. Но как раз ограничения и порождают трудности, связанные не просто с поиском max и min при отсутствии ограничений, а с необходимостью учета таких ограничений. Искать требуется не просто экстремум, а условный экстремум. Методы решения задачи позволяют учитывать особенности структуры задачи и даже отказаться от симплексного метода решения в чистом виде.
I. Основные параметры, термины и обозначения
Для ощущения масштаба задачи приведу парочку изображений того, что рассматривается в транспортной задаче линейного программирования.
Все суда на одной карте в режиме онлайн
Все самолеты мира в режиме онлайн
В теории в тексте задачи Хичкока ничего не говорится о равенстве имеющегося общего запаса судов в портах отправления и общей потребности в судах в портах прибытия (назначения). Если такого равенства нет, то система ограничений несовместна. В случае равенства
транспортная задача называется «сбалансированной». Задачи, в которых условие баланса не задано, должны быть приведены к «сбалансированному» виду. Это можно выполнить использованием «фиктивных» перевозок. Рассматриваем два случая:
Метод содержит три последовательных этапа:
Формирование опорного плана;
Проверка опорного плана на оптимальность;
Переход к новому опорному плану, если предыдущий не оптимален.
II. Формирование опорного плана перевозок
Рассмотрим способ получения начального опорного плана транспортной задачи, названный способом северо-западного (С-З) угла. Способ заключается в заполнении ячеек таблицы m×n значениями переменной xij, таким образом, чтобы удовлетворялись условия задачи. При этом план решения Х[m, n] может быть и не оптимальным, но обязательно должен быть допустимым.
В этом способе формируют опорный план, двигаясь по таблице: сверху вниз по строкам и слева направо вдоль строки. Начинают с левого верхнего угла (ячейки), куда вписывают значение x11 =min<a1, b1>.Первые строка и столбец из рассмотрения далее исключаются.
Затем, если a1 > b1, то определяется остаток (a1 – b1) продукта на первом пункте отправления и его запас реализуется на 2-м пункте назначения. Остаток потребностей 2-го пункта назначения удовлетворяется за счет 2-го пункта отправления, остатки которого направляются в 3-й пункт назначения и т.д. Ниже метод будет иллюстрирован числовым примером.
Пример 1. Построение опорного плана методом Северо-Западного угла
Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные хij задачи Q.
РЕШЕНИЕ Построить исходный опорный план способом северо-западного угла. Строим симплексную таблицу: Таблица 3. Опорный план задачи
В таблице способом северо-западного угла получен опорный план. Базисные переменные (их число = 6): x11 = 40, x12= 20, x22= 40, x23= 40, x33= 40, x34= 60. Свободные переменные: x13= x14= x21= x24= x31= x32= 0 (их число равно 6).
Ячейки таблицы, соответствующие базисным переменным, называют базисными, остальные – свободными. Далее в алгоритме будем следовать идее симплекс метода. Суммарная стоимость перевозок Q, соответствующая плану Х[m,n], получает представление
Q = d11∙x11 + d12∙x12 + d22∙x22 + d23 ∙x23+ d33 ∙x33+ d34 ∙x34 = = 5∙40 + 2∙20 + 10∙40 + 2∙40 + 8∙40 + 5∙60 = 200+40+400 + 80 + 320+ 300 = 1340 ед
Каждому из таких уравнений соответствует какая-либо базисная переменная хij Система уравнений с потенциалами содержит m+n неизвестных потенциалов, число же уравнений равняется числу базисных ячеек таблицы, т.е. (m + n – 1). Следовательно, один из потенциалов можно задать произвольно, положив его равным, например, нулю.
Решая далее систему уравнений для потенциалов, находим значения потенциалов строк и столбцов, все фиктивные стоимости dij и коэффициенты γij. Если для всех свободных клеток γrs ≤ 0, то перевод в базис любой свободной переменной не уменьшит значения целевой функции и, следовательно, выбранный опорный план не является оптимальным. Если же некоторые γrs >0, то данный план можно улучшить путем перевода в базис свободной переменной, соответствующей max γrs, а также путем исключения из базиса, принадлежащей ему переменной, первой обращающейся в нуль. Переход к новому опорному плану и поиск оптимального плана рассмотрим на примере. Другой способ формирования опорного плана предложен Фогелем. Этот способ при первом чтении можно пропустить, так как дальше он в тексте не используется.
Пример 2. Способ аппроксимации Фогеля
В большинстве случаев этот способ дает опорный план наиболее близкий к оптимальному. Удобен для матриц большой размерности. Используется концепция штрафов, взимаемых за выбор не самого оптимального с точки зрения транспортных издержек маршрута. Штраф по каждой строке и каждому столбцу определяется из анализа маршрутов с различными показателями издержек (как разность двух различных уровней транспортных издержек). Первой заполняется клетка матрицы (таблицы), в которой фиксируется самый крупный штраф. После заполнения клетки штрафы пересчитываются и так до тех пор, пока все ресурсы не будут распределены. Исходные данные для этого примера заполняют таблицу слева вверху.
Этапы алгоритма: 1. Вычисление разностей в каждой строке и в каждом столбце между наименьшей стоимостью и ближайшей к ней по величине. Разности по строкам записываются справа в столбце разностей, разности по столбцам – внизу в строке разностей. Например, для строк А1 разность равна А1В2 – А1В3 = 38 – 24 = 14 и т. д.
2. Поиск из всех разностей, как по строкам, так и по столбцам максимальный. В нашем примере максимальная разность равна 38 и находится в строке А2. Обведем максимальную разность рамкой.
3. Размещение в клетку, где находится наименьшая стоимость (А2В2 = 18) (строка с наибольшей разностью), максимально возможного количества ресурсов. Оно равно 20, т.е. всему ресурсу отправителя А2. Поскольку все ресурсы отправителя А2 исчерпаны, строку А2 исключаем из дальнейших расчетов, для чего отметим все клетки этой строки точками.
4. Вычисление разностей столбцам и строкам, не принимая во внимание стоимость в клетках, имеющих ресурсы и клетках с точкой (исключенную строку или столбец) и определение максимальной разности в строке или столбце (В3 = 76).
5. Поиск минимального элемента в строке или в столбце с максимальной разностью (А1В3 = 24) и размещения в данную клетку максимально возможного количества ресурса, возвращение к этапу №4 и т.д. Окончательно
ЦФ Q=23∙19 + 7∙3 + 20∙18 + 2∙10 + 14∙24 + 1∙100 +3∙48 = = 437 + 21 + 360 + 20 +3 36 + 100 + 272 =1546 ед. Это значение соответствует опорному плану Фогеля.
III. Транспортная задача линейного программирования
Как основной метод решения транспортной задачи – используется метод потенциалов. Ни симплексный метод, ни распределительный метод здесь не рассматриваются. У них имеются свои плюсы и минусы, но объем изложения достаточно велик. Возможно этому позднее я уделю внимание и время, но пока отвечаю на пожелание читателя Хабра.
Исходные данные задачи удобно представить двумя матрицами.
Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные хij задачи
Решение задачи:
1. Формирование начального опорного плана способом Северо-Западного угла.
2. Проверка опорного плана на оптимальность
Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов. Определим систему уравнений для потенциалов и вычислим их значения:
α1 + β1 = d11 = 2;
α1 + β2 = d12 = 3;
α2 + β2 = d22 = 3;
α2 + β3 = d23 = 1;
α2 + β4 = d24 = 2;
α3 + β4 = d34 = 2.
Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β1 = 0. Тогда после решения системы получены значения потенциалов: α1= 2, α2= 2, α3= 2, β1 =0, β2=1, β3 =–1, β4 =0,
Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].
Выделяем в Г [m, n] свободные ячейки, содержащие γrs. Проверяем наличие положительных переменных γi,j > 0. Так как в матрице (в свободных ячейках) имеем γ32 = 2 > 0, то исходный опорный план может быть улучшен, он не является оптимальным.
3. Переход к новому (улучшенному) опорному плану
Переменную x32 =x следует ввести в базис. Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок
Модификация начального опорного плана
Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок Очевидно, что наибольшее x определяется теми xij в базисных клетках, из которых этот х вычитается. Следовательно, x11 = min<х22, х34> = <10, 40>= 10. При x >10 перевозка х22 становится отрицательной. Переменную х22 исключаем из базиса и переводим ее в разряд свободных переменных. Далее повторяются рекурсивно три пункта алгоритма.
Получаем из модифицированного плана новый опорный план
В нем объемы перевозок распределены иначе чем в начальном опорном плане.
Новый опорный план
Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d11 ∙x11 + d12∙x12 + d23∙x23 + d32∙x32 + d24∙x24+ d34∙x34 =
=2∙70 + 3∙20 + 2∙10 + 1∙20 + 1∙10 + 2∙30 = 140 + 60 + 20 + 20 + 10 + 60 = 310 ед. Затраты на перевозки при этом плане уменьшились на 330 – 310 = 20 ед.
Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.
2. Проверка опорного плана на оптимальность
Определим систему уравнений для потенциалов и вычислим их значения:
α1 + β1 = d11 = 2;
α1 + β2 = d12 = 3;
α2 + β3 = d23 = 1;
α2 + β4 = d24 = 2;
α3 + β2 = d32 = 1;
α3 + β4 = d34 = 2.
Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пустьα1 = 0. Тогда после решения системы получены значения потенциалов: α1= 0, α2= – 2, α3= –2, β1 =2, β2=3, β3 = 3, β4 =4.
Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].
Свободные ячейки матрицы Г [m, n] содержат γi,j > 0 (γ14 = 1>0). План не оптимален.
3. Переход к новому (улучшенному) опорному плану
Из свободных переменных с xij > 0, выбираем одну x14 для введения ее в базис. Обозначим ее как и ранее через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся очередным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок
модифицированный план
Очевидно, что наибольшее x определяется теми xij в базисных клетках, из которых этот х вычитается. Следовательно, x11 = min<х12, х34> = <20, 30>= 20. При х12 >20 перевозка х12 становится отрицательной. Переменную х12 исключаем из базиса и переводим ее в разряд свободных переменных. Переходим к новой итерации
1. Получаем из модифицированного плана новый опорный план.
В нем объемы перевозок распределены иначе чем в предшествующем опорном плане.
Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d11 ∙x11 + d14∙x14 + d23∙x23 + d32∙x32 + d24∙x24+ d34∙x34 =
=2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 140 + 60 + 20 + 20 + 30 + 20 = 290 ед. Затраты на перевозки при этом плане уменьшились на 310 – 290 = 20 ед. Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.
2. Проверка опорного плана на оптимальность
Определим систему уравнений для потенциалов и вычислим их значения:
α1 + β1 = d11 = 2;
α1 + β4 = d14 = 3;
α2 + β3 = d23 = 1;
α2 + β4 = d24 = 2;
α3 + β2 = d32 = 1;
α3 + β4 = d34 = 2. Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β1 = 0. Тогда после решения системы получены значения потенциалов: α1= 2, α2= 2, α3= 2, β1 =0, β2=1, β3 =–1, β4 =0.
Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].
При переходе к новому опорному плану проверяем наличие положительных свободных переменных γi,j >0. Но таких переменных не оказалось. Отсюда следует вывод, что полученный последним модифицированный план является оптимальным и ему соответствует значение линейной формы
Q’= 2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 290.
Заключение
Вся теория исследования операций с позиций математики решает неклассические задачи оптимизации целевых функций. Отличие от классики в том, что те ограничения на переменные, которые исследователи вынуждены накладывать в рамках моделей, созданы и вызваны реальностью. Отыскивать требуется экстремумы функций при многих ограничениях, так называемые условные экстремумы. Классика не позволяет этого делать. Взятие производных и приравнивание их нулю «не видит» ограничений. Лучшее, что там имеется это функция Лагранжа, но ее использование также весьма ограничено. Транспортные задачи – частный, но важный случай в исследовании операций. Надеюсь, что читатель разобравшись в приведенных примерах, лучше стал понимать логику задачи и сумеет самостоятельно постигать интересующие его вопросы по другим публикациям в учебниках и журнальных статьях.
Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.
Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.
Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.
Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.
Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.
Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.
Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.