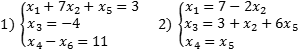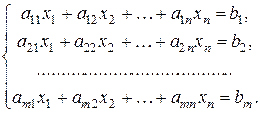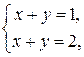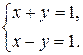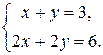Что такое определенная система

Системы линейных уравнений: основные понятия

— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x ₁, x ₃ и x ₄. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x ₁, x ₃ и x ₅. Достаточно переписать самое последнее уравнение в виде x ₅ = x ₄.

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

Так, в приведенных выше системах переменные x ₂, x ₅, x ₆ (для первой системы) и x ₂, x ₅ (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.

И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.

Источник

Основные понятия. Системы линейных уравнений

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

ЛЕКЦИЯ 4

Системы линейных уравнений. Основные понятия: совместные и несовместные, определенные и неопределенные системы. Метод Гаусса. Общее решение. Теорема Кронекера-Капелли. Исследование на совместность систем линейных уравнений. Однородные системы и свойства их решений. Фундаментальная система решений.

Рассмотрим произвольную систему линейных уравнений

Решением системы называется такая совокупность n чисел 1,a₂. a_n>, которая при подстановке в данную систему на место не известных x₁,x₂. x_n преобразует все уравнения в тождества. Задача теории систем линейных уравнений состоит в том, чтобы найти все решения системы. При этом возможны три случая.

1) Система вообще не имеет решений. Системы линейных уравнений, не имеющие ни одного решения, называются несовместными. Например, система уравнений

несовместна. С геометрической точки зрения, это соответствует двум параллельным несовпадающим прямым плоскости xOy.

2) Если система, имеющая хотя бы одно решение, называется совместной. Совместные системы могут иметь либо одно решение, либо бесконечно много решений. Системы, имеющие только одно решение, называются определенными. Например,

С геометрической точки зрения, это соответствует двум пересекающимся прямым плоскости xOy.

3) Система, имеющая бесконечно много решений, называется неопределенной. Например,

С геометрической точки зрения, это соответствует двум совпадающим прямым плоскости xOy.

Историческая справка. В трактатах до XIX в. рассматривались только квадратные системы линейных уравнений, т.е. системы, у которых число неизвестных равно числу уравнений. В случае несовместных или неопределенных систем довольствовались замечанием о некорректно поставленной задаче. В 1849 г. К. Гаусс (1777-1855) исследовал алгоритм последовательного исключения неизвестных для решения произвольных систем линейных уравнений, который с различными модификациями применяется до сих пор в практических вычислениях. Введение 1877 г. Г. Фробениусом (1849-1897) понятия ранга матрицы, позволило явно выразить условие совместности и определенности систем линейных уравнений через ее коэффициенты (теорема Кронекера-Капелли). Эта теорема содержалась в лекциях, прочитанных Л. Кронекером (1823-1891) в 1883-91 гг. А. Капелли (1858-1892) впервые дал формулировку теоремы с использованием термина «ранг» (1892 г.). К концу XIX в. усилиями К. Вейерштрасса (1815-1897), М. Жордана (1838-1922), Г. Фробениуса, Ш. Эрмита (1822-1901) и др. было завершено построение общей теории систем линейных уравнений.

Источник

Как решать систему уравнений

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует данному уравнению и является верным числовым равенством.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

Выразим x из первого уравнения:

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

Из первого уравнения выразим x:

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

Уравнять модули коэффициентов при одном из неизвестных.

Сложить или вычесть уравнения.

Решить полученное уравнение с одной переменной.

Подставить поочередно каждый из найденных корней в одно из уравнений исходной системы. Найти второе неизвестное.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести к нормальному виду это уравнение

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

Задание 4. Решить систему уравнений

Задание 5. Как решить систему уравнений с двумя неизвестными

Источник

Что такое определенная система

Дадим ряд необходимых определений.

Система линейных уравнений называется неоднородной, если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее свободные члены равны нулю.

Решением системы уравнений называется упорядоченный набор чисел, который, будучи подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Рассмотрим неоднородную систему линейных алгебраических уравнений, имеющую при n = m следующий общий вид:

Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:

Определитель главной матрицы системы называется главным определителем и обозначается ∆.

Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:

Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).

После этого следует провести проверку полученного решения.

Пример 1.4. Решить систему методом Крамера

Решение. Так как главный определитель системы

отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители

Воспользуемся формулами Крамера (1.6):

Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.

Определить стоимость 1 единицы продукции молокоцеха каждого вида.

Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:

Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):

Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):

По формулам Крамера (1.6) имеем:

Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей

Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.

В MathCAD для нахождения определителя пользуются палитрой оператора Matrix

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Системы линейных уравнений

Можно доказать (см. результаты ☟ НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:

1. система совместна и имеет единственное решение;

2. cистема совместна и имеет бесконечное множество решений;

3. cистема несовместна.

Матричная форма записи

Исключение переменных (метод Гаусса)

метода достаточно проста.

Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями — те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.

Исключение переменных

Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:

1. перестановка двух уравнений;

2. умножение обеих частей уравнения на любое отличное от нуля число;

Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.

Задача. С помощью элементарных преобразований привести систему л.у. к наиболее простому виду: такому, из которого легко было бы установить множество решений.

Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.

Исторический комментарий о Гауссе ☞ ЗДЕСЬ.

Установление множества решений

Пример. Решить систему л.у.

Ответ. Система несовместна.

Пример. Решить систему л.у.

Дальнейший матричный анализ метода Гаусса ☞ ЗДЕСЬ.

Формулы Крамера

Теорема. Cистема

Доказательство ☞ ЗДЕСЬ

Пример. Решить систему уравнений

Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее ☞ ЗДЕСЬ.

Найти достаточное условие существования общего решения систем уравнений:

Теорема Кронекера-Капелли

Доказательство достаточности проводится в следующем пункте. ♦

Система однородных уравнений

Доказать, что для совместности системы

An elementary treatise on determinants

в следующей формулировке.

Ответ ☞ ЗДЕСЬ

Общее решение

Пример. Исследовать совместность и найти общее решение системы уравнений:

Теперь посмотрим как можно описать общее решение однородной системы.

Система однородных уравнений

Теперь обсудим способы нахождения ФСР.

Оформим этот способ построения ФСР в теорему:

Пример. Найти ФСР для системы уравнений

Пример. Найти ФСР для системы уравнений

3. Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.

Пример. Найти ФСР для системы уравнений

Геометрическая интерпретация

Статья не закончена!

Ортогональность

Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти ☞ ЗДЕСЬ.

Источник