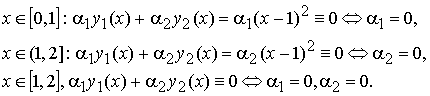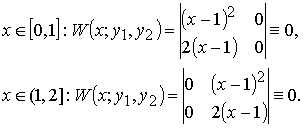Что такое определитель вронского для дифференциального уравнения

Определитель Вронского

Вторая сторона медали, которую мы сейчас будем обсуждать. это определитель Вронского. Так же, как и для уравнений n-го порядка, он возникает при попытке найти ту линейную комбинацию

которая удовлетворяет заданному начальному условию ж(/,о) = Т что сводится к решению векторного уравнения

Нетрудно видеть, что матрица, определитель которой нас интересует, это матрица, столбцы которой есть просто решения x l (t).

Определение 18.5 Пусть

набор вектор-функций, являющихся решениями системы (18.5). Тогда определитель

называется определителем Вронского 6 системы решений ж 1 (?). x n (t).

Теорема 18.2 Пусть ж 1 (t), ar(f). x n (t) некоторый набор решений системы (18.5). Тогда следующие пять утверждений эквивалентны:

“Название „определитель Вронского» (или более коротко „вронскиан») оправ- дывается не только происхождением. Если рассмотреть линейное уравнение n-го порядка

x 2 (t*), x n (t*) линейно зависима;

Следствие. Эквивалентны и противоположные утверждения:

I) система вектор-функций x l (t), x 2 (t). x n (t) линейно независима на (а, /3):

и перейти к эквивалентной системе

то, поскольку мы обозначили мри этом Xi = Х,Х2 = Х. Х_п = Х^ п 1 ‘, каждому решению 4>jуравнения будет соответствовать решение

Определитель Вронского, построенный но набору решений векторной системы окажется тогда равным

то есть совпадет в точности с определителем Вронского для системы решений исходного уравнения. Таким образом, определитель Вронского для решений уравнений и определитель Вронского для решений эквивалентной ему системы не просто аналогичны они в точности совпадают друг с другом.

5) существует такое t* € (а,/3), что W(t*) ф 0.

Доказательство теоремы проводится но схеме 1=>2=>3=>1с дополнительными „довесками 11 2 4 и 3 5.

Эквивалентности 2 о 4 и 3 О 5 являются по существу хороню известным утверждением из алгебры о том. что определитель матрицы равен нулю тогда и только тогда, когда ее столбцы линейно зависимы.

Импликацию 1 =>• 2 мы уже обсуждали из линейной зависимости вектор-функций следует линейная зависимость векторов при каждом t. Импликация 2 => 3 тривиальна. Остается доказать самое существенное импликацию 3 => 1.

и построим линейную комбинацию наших решений с теми же коэффициентами:

Эта функция будет решением системы (18.4) и будет удовлетворять нулевому начальному условию при t = t*:

Поскольку нулевому начальному условию удовлетворяет также еще одно очевидное решение системы нулевое то. по теореме существования и единственности (здесь мы пользуемся именно единственностью), два указанных решения обязаны совпадать. Но x= 0 означает, что нетривиальная линейная комбинация вектор-функций x l (t) равна нулю:

Линейная зависимость системы вектор-функций x lдоказана. Доказательство теоремы завершено.

Источник

Вронскиан

Вронскиа́н (определитель Вронского) системы функций , дифференцируемых на промежутке (n-1)-раз — функция на , задаваемая определителем следующей матрицы:

.

Также вронскианом называют функцию, заданную определителем более общего вида. А именно, пусть задано n вектор-функций с n компонентами: . Тогда определитель будет выглядеть так (чтобы избежать разночтений обозначим его ):

.

Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми. Это помогает в поиске его общего решения.

Содержание

Свойства

Примеры

Есть точки, где вронскиан отличен от нуля (в нашем случае это любая точка, кроме x=0). Поэтому на любом промежутке эти функции будут линейно независимыми.

Обе функции всюду дифференцируемы (в том числе в нуле, где производные обеих функций обращаются в ноль). Убедимся, что вронскиан всюду ноль.

Однако эти функции, очевидно, являются линейно независимыми. Видим что равенство вронскиана нулю не влечёт за собой линейной зависимости в случае произвольного выбора функций.

См. также

Литература

Полезное

Смотреть что такое «Вронскиан» в других словарях:

Вронскиан — функциональный определитель, составленный из n функций f1(x), f2(x), …, fn (x) и их производных до n 1 порядка включительно: Обращение В. в нуль [W (x) = 0] является необходимым, а при некоторых дополнительных… … Большая советская энциклопедия

ВРОНСКИАН — определитель Вроньского, определитель системы пвектор функций размерности п имеющий вид: В. системы n скалярных функций имеющих производные до ( п 1) го порядка включительно, есть определитель Это понятие было введено Ю. Вроньским [1]. Если… … Математическая энциклопедия

Вроньский Юзеф — (Wroński), настоящая фамилия Хёне (Hoene) (1776 1853), польский математик и философ мистик. Известен введённый им определитель, важный в теории линейных дифференциальных уравнений (вронскиан). * * * ВРОНЬСКИЙ Юзеф ВРОНЬСКИЙ (наст. фам. Хене,… … Энциклопедический словарь

ВРОНЬСКИЙ Юзеф — ВРОНЬСКИЙ (наст. фам. Хене Hoene) Юзеф (1776 1853), польский математик и философ мистик. Известен введенный им определитель, важный в теории линейных дифференциальных уравнений (вронскиан) … Большой Энциклопедический словарь

Вроньский Юзеф — Вроньский (Wroński) Юзеф (настоящая фамилия ‒ Хёне, Hoene; известен также как Гёне Вронский) (24.8.1776, Вольштын, ‒ 9.8.1853, Париж), польский математик и философ мистик. Был артиллерийским офицером в армии Костюшко, впоследствии служил в штабе… … Большая советская энциклопедия

Источник

Определитель Вронского

Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми.

Свойства определителя Вронского

Есть точки, где вронскиан отличен от нуля (в нашем случае это любая точка, кроме x=0). Поэтому на любом промежутке эти функции будут линейно независимыми.

3. Приведём теперь пример, когда вронскиан всюду равен нулю, но функции всё равно линейно независимы. Зададим две функции:

Обе функции всюду дифференцируемы (в том числе в нуле, где производные обеих функций обращаются в ноль). Убедимся, что вронскиан всюду равен нулю:

Однако эти функции, очевидно, являются линейно-независимыми. Видим, что равенство вронскиана нулю не влечёт за собой линейной зависимости в случае произвольного выбора функций.

Системы линейных дифференциальных уравнений

Определение. Система Дифференциальных Уравнений называется линейной, если она линейна относительно всех неизвестных функций и их производных.

Общий вид системы дифференциальных уравнений

то решение будет единственным при условии, что вектор-функция непрерывна на и коэффициенты матрицы: тоже непрерывные функции.

в ином случае оно называется неоднородным.

Так как оператор линейный, то для него выполняются следующие свойства:

Источник

Что такое определитель вронского для дифференциального уравнения

Если \(\left( x \right),\left( x \right)\) − фундаментальная система решений, то общее решение уравнения второго порядка представляется в виде \[y\left( x \right) = \left( x \right) + \left( x \right),\] где \(, \) − произвольные постоянные.

Заметим, что по заданной фундаментальной системе решений \(\left( x \right),\left( x \right)\) можно построить соответствующее однородное дифференциальное уравнение. Для случая второго порядка такое уравнение выражается через определитель в виде: \[\left| <\begin<*<20>> <>&<>&y\\ <>&<>&y’\\ <>&<>&y» \end> \right| = 0.\]

Итак, как указано выше, общее решение однородного дифференциального уравнения второго порядка является линейной комбинацией двух линейно независимых частных решений \(\left( x \right),\left( x \right)\) этого уравнения.

Очевидно, что частные решения зависят от коэффициентов дифференциального уравнения. Формула Лиувилля-Остроградского устанавливает связь между вронскианом \(W\left( x \right),\) построенном на базе частных решений \(\left( x \right),\left( x \right),\) и коэффициентом \(\left( x \right)\) в дифференциальном уравнении.

К сожалению, общего метода отыскания частного решения не существует. Обычно это можно сделать путем подбора.

Если известно частное решение \(\left( x \right) \ne 0\) линейного однородного уравнения второго порядка, то его можно преобразовать к линейному уравнению первого порядка с помощью подстановки \(y = \left( x \right)z\left( x \right)\) и последующей замены \(z’\left( x \right) = u.\)

Другой способ понижения порядка основан на использовании формулы Лиувилля-Остроградского. Здесь также одно частное решение \(\left( x \right)\) должно быть известно. Соответствующие примеры разобраны ниже.

Таким образом, общее решение имеет вид: \[ + 1> \right)z > = <x + \left( <+ 1> \right)\arctan x + \left( <+ 1> \right) > = <\left[ + 1> \right)\arctan x> \right] + \left( <+ 1> \right).> \]

Поскольку частное решение \(\) известно, то мы получили дифференциальное уравнение первого порядка для определения другого частного решения \(.\) После деления на \(y_1^2\) имеем: \[ <\left. < — = > \right|:y_1^2,>\;\; <\Rightarrow \frac<< — >><> = \frac<<>><>,>\;\; <\Rightarrow <\left( <\frac<<>><<>>> \right)^\prime > > = <\frac<<>><> > = <\frac<<\cancel>><<\cancel>> = .> \] Отсюда находим функцию \(:\) \[ <\frac<<>><<>> = x + ,>\;\; <\Rightarrow = \left( <x + > \right) > = <\left( <x + > \right) > = < + ,> \] где \(,\) \(\) − постоянные интегрирования. Ясно, что функция \(\) фактически представляет собой общее решение уравнения.

Источник

Определитель Вронского. Формула Остроградского-Лиувилля.

Справедливо следующее необходимое условие линейной зависимости функций.

Важно понимать, что обратное утверждение неверно. Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Однако, если определитель Вронского системы функций на некотором отрезке отличен от тождественного нуля, то система функций линейно независима на этом отрезке.

Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Рассмотрим две функции:

Эти функции линейно независимы на [0, 2]. Действительно:

Этот пример означает, что тождественное равенство нулю определителя Вронского системы функций является необходимым условием линейной зависимости системы функций, но не является достаточным условием линейной зависимости системы функций.

С другой строны, отличие от тождественного нуля определителя Вронского системы функций является достаточным условием условием линейной независимости системы функций.

(Ведь если бы она была бы линейно зависима, то определитель Вронского был бы тождественным нулём).

Формула Лиуви́лля-Острогра́дского — формула, связывающая определитель Вронского (вронскиа́н) для решений дифференциального уравнения и коэффициенты в этом уравнении.

Пусть есть дифференциальное уравнение вида

тогда где — определитель Вронского

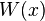
Для линейной однородной системы дифференциальных уравнений

где — непрерывная квадратная матрица порядка , справедлива формула Лиувилля-Остроградского

где — след матрицы

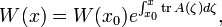
Построение общего решения линейного однородного уравнения 2 – го порядка с постоянными коэффициентами.

Однородное уравнение второго порядка:

интегрируется следующим образом:

Пусть — корни характеристического уравнения.

,

являющегося квадратным уравнением.

Вид общего решения однородного уравнения зависит от значения дискриминанта :

· при уравнение имеет два различных вещественных корня

Общее решение имеет вид:

· при — два совпадающих вещественных корня

Общее решение имеет вид:

· при существуют два комплексно сопряженных корня

Общее решение имеет вид:

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Источник