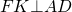Что такое оси симметрии 3 класс прямоугольника
Прямоугольник. Ось симметрии фигуры
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
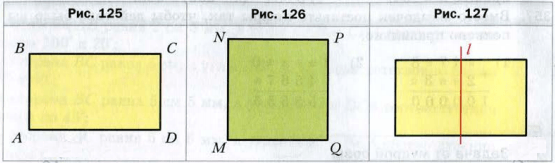
На рисунке 125 изображен прямоугольник ABCD.
Стороны AB и BC имеют общую вершину B. Их называют соседними сторонами прямоугольника ABCD. Также соседними являются, например, стороны BC и CD.
Соседние стороны прямоугольника называют его длиной и шириной.
Стороны AB и CD не имеют общих вершин. Их называют противоположными сторонами прямоугольника ABCD. Также противолежащими являются стороны BC и AD.
Противолежащие стороны прямоугольника равны.
На рисунке 125 AB = CD, BC = AD. Если длина прямоугольника равна a, а ширина − b, то его периметр вычисляют по уже знакомой тебе формуле:
P = 2 a + 2 b
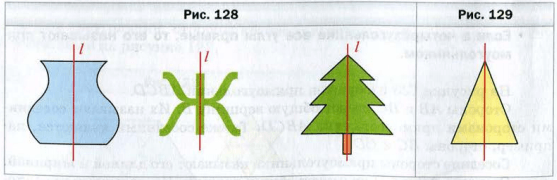
Прямоугольник, у которого все стороны равны, называют квадратом (рис. 126 ).
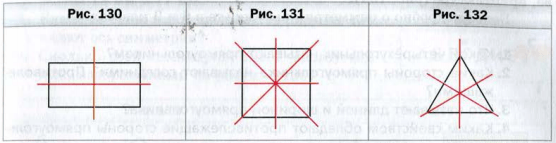
Проведем прямую l, проходящую через середины двух противолежащих сторон прямоугольника (рис. 127 ). Если лист бумаги перегнуть по прямой l, то две части прямоугольника, лежащие по разные стороны от прямой l, совпадут.
Итак, прямоугольник − это фигура, имеющая ось симметрии. Также ось симметрии имеет равнобедренный треугольник (рис. 129 ).
Фигура может иметь более одной оси симметрии. Например, прямоугольник, отличный от квадрата, имеет две оси симметрии (рис. 130 ), а квадрат − четыре оси симметрии (рис. 131 ). Равносторонний треугольник имеет три оси симметрии (рис. 132 ).
Объекты, имеющие ось симметрии, легко воспринимаются и приятные для глаза. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота».
Идея симметрии широко используется в изобразительном искусстве, архитектуре (рис. 134 ).
Симметрия прямоугольника
Какова симметрия прямоугольника? Есть ли у прямоугольника ось симметрии и центр симметрии?

Осями симметрии прямоугольника являются прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

Прямоугольные треугольники AOK и DOK равны по катету и гипотенузе (OK- общий катет, OA=OD по свойству диагоналей параллелограмма). Следовательно, AK=DK, то есть прямая FK проходит через середину стороны AD.
Отметим на стороне AB произвольную точку X. Проведём прямую через точку X прямую, перпендикулярную прямой FK. Точки пересечения этой прямой с прямыми FK и CD обозначим через P и X1.
Четырёхугольники AXPK и KPX1D — прямоугольники (так как у них все углы прямые). Следовательно, XP=AK, PX1=KD. А так как AK=DK, то и XP=PX1. Значит, X1 — точка, симметричная точке X относительно прямой FK.
Имеем: точка, симметричная относительно прямой FK произвольной точке прямоугольника, также принадлежит прямоугольнику.
Точки F и K симметричны сами себе относительно прямой FK.
Таким образом, FK — ось симметрии прямоугольника.
Аналогично доказывается, что прямая, проходящая через точку O параллельно AD является осью симметрии ABCD.
Прямоугольник — центрально симметричная фигура.
Центром симметрии параллелограмма является точка пересечения его диагоналей.
Так как параллелограмм — центрально-симметричная фигура с центром симметрии в точке пересечения диагоналей, то это верно и для частного случая параллелограмма — прямоугольника.
Прямоугольник. Ось симметрии фигуры
Если в четырёхугольнике все углы прямые, то его называют прямоугольником.
На рисунке изображён прямоугольник ABCD.
Стороны AB и BC имеют общую вершину B. Их называют соседними сторонами прямоугольника ABCD. Также соседними являются, например, стороны CD и AD.
Соседние стороны прямоугольника называют его длиной и шириной.
Стороны AB и CD не имеют общих вершин. Их называют противолежащими сторонами прямоугольника ABCD. Также противолежащими являются стороны BC и AD.
Противолежащие стороны прямоугольника равны.
На рисунке AB=CD, BC=AD. Если длина прямоугольника равна a, а ширина – b, то его периметр вычисляют по уже знакомой нам формуле:
P=2a+2b
Прямоугольник, у которого все стороны равны, называют квадратом. Квадрат ещё называют правильным четырёхугольником.
Проведём прямую с, проходящую через середины двух противолежащих сторон прямоугольника. Если лист бумаги перегнуть по прямой с, то две части прямоугольника, лежащие по разные стороны от прямой с, совпадут.
Аналогичным свойством обладают фигуры, изображённые на рисунке. Такие фигуры называют симметричными относительно прямой. Прямую с называют осью симметрии фигуры.
Прямоугольник – это фигура, имеющая ось симметрии. Также ось симметрии имеет равнобедренный треугольник.
Фигура может иметь более одной оси симметрии. Например, прямоугольник, отличный от квадрата, имеет две оси симметрии, а квадрат – четыре оси симметрии. Равносторонний треугольник имеет три оси симметрии.
Изучая окружающий мир, мы часто встречаемся с симметрией. Объекты, имеющие ось симметрии, легко воспринимаются и приятны для глаз. Недаром в Древней Греции слово “симметрия” служило синонимом слов “гармония”, “красота”. Идея симметрии широко используется в изобразительном искусстве, архитектуре.
Поделиться ссылкой:
Добавить комментарий Отменить ответ
Рубрики
Свежие записи
Презентация на тему по математике «Прямоугольник. Ось симметрии»
Описание презентации по отдельным слайдам:
Описание слайда:
Прямоугольник. Ось симметрии фигуры
Описание слайда:
Если в четырехугольнике все углы прямые, то его называют прямоугольником
А B
Описание слайда:
Описание слайда:
Противолежащие стороны прямоугольника равны.
АD=BC и АB=DC
Описание слайда:
КВАДРАТ – это прямоугольник у которого все стороны равны
MNPQ – квадрат
Q P
MN=NP=PQ=QM
Описание слайда:
ОСЬ СИММЕТРИИ ФИГУРЫ
L – ось симметрии фигуры
Описание слайда:
Слово «симметрия» греческое ( συμμετρία), оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”, неизменность при каких-либо преобразованиях.
Описание слайда:
Фигуры, симметричные относительно прямой
Описание слайда:
Прямоугольник – 2 оси симметрии,
квадрат – 4 оси симметрии,
равносторонний треугольник –
3 оси симметрии.
Описание слайда:
Изучая окружающий мир, мы часто встречаемся с симметрией.
Описание слайда:
Идея симметрии широко используется в изобразительном искусстве, архитектуре.
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Работа с учебником
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Презентация к уроку по математике «Знакомство с десятичными дробями»
Методический материал «Математические диктанты»
Полугодовая контрольная работа 6 класс
Конспект урока по математике в 5 классе «Знакомство с десятичными дробями»
Презентация по математике «Проект. Математическая сказка»
Презентация «Поиск идеального портфеля.»
Статья «Поиск идеального портфеля.»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5336774 материала.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Дополнительные занятия по изучению культуры чеченского народа появятся в школах Чечни
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
На новом «Уроке цифры» школьникам расскажут о разработке игр
Время чтения: 1 минута
Российские школьники установили рекорд на олимпиаде по астрономии
Время чтения: 2 минуты
Кузнецова призвала разработать закон о психологической помощи
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Чёрная пятница
На все курсы повышения квалификации и профессиональной переподготовки
Прямоугольник. Ось симметрии фигуры
Урок 15. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Прямоугольник. Ось симметрии фигуры»
Давайте представим себе такую историю.
– Саша, чем ты занимаешься? – поинтересовался у друга Паша.
– Папа научил меня делать самолётик оригами! – восхищался Саша. – Посмотри, как круто летает такой самолётик!
– Да… его полёт завораживает! – наблюдал за самолётиком Паша. – Только вот я бы уточнил, что искусство создания бумажных самолётиков называется аэрогами или бумажная авиация. Это одна из техник оригами, при которой необходимо не только сложить красивую фигурку, похожую на оригинал, но и предусмотреть её лётные характеристики. Самолёты из бумаги были известны более 2000 лет назад. Однако тогда это были не самолётики, а птички.
Датой создания бумажного самолётика считается 1909 год, но более популярной датой является 1930 год. Тогда основатель известной компании по аэродинамике Lockheed Corporation Джек Нортроп заинтересовался, как из бумаги сделать самолёт.
– А зачем этому человеку нужны были бумажные самолётики? – поинтересовался Паша.
– Изобретатель хотел протестировать на бумажных самолётах свои новые идеи, – продолжил Паша. – Использование бумажной подделки в воздухе помогало правильно подбирать форму для будущих летательных аппаратов.
– Как же это интересно! – с восторгом сказал Саша.
– И это ещё не всё! – продолжил Паша. – В наши дни бумажная авиация, или аэрогами, получила мировую известность. Каждый человек знает, как сложить элементарный самолётик и запустить его. Но на сегодняшний день это уже не просто забава, а серьёзное увлечение, по которому проводят соревнования по всему миру.
– Вот бы мне побывать на таких соревнованиях, – сказал Саша.
– Обязательно побываешь! – подбодрил друга Паша. – Главное верить в свою мечту! Ну и, конечно же, тебе ещё будет полезным познакомиться с условиями создания и схемами бумажных самолётиков. Одними из главных условий создания самолётика являются использование бумаги прямоугольной или квадратной формы и чёткое соблюдение симметрии.
– Ого! – задумался Саша. – Вот про прямоугольные и квадратные формы я всё знаю, а про симметрию совсем ничего, – расстроился он.
– А давай спросим у Электроши, – предложил Паша. – Он точно всё знает!
– Ребята, прежде чем я вам расскажу о прямоугольниках и симметрии, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– А теперь поговорим о прямоугольниках, – предложил Электроша. – И сразу начнём с вопроса: как вы понимаете, что такое прямоугольник?
– Прямоугольник – это четырёхугольник, у которого все углы прямые, – ответил Паша.
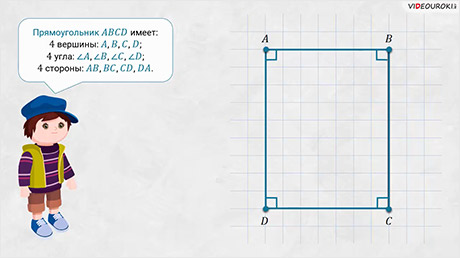
– Молодец! – похвалил Пашу Электроша. – Посмотрите: на листе изображён прямоугольник ABCD. Вы уже знакомы с элементами многоугольников. Назовите элементы нашего прямоугольника.
– Прямоугольник ABCD имеет 4 вершины: А, B, C и D, 4 одноимённых угла и 4 стороны: AB, BC, CD и DA – ответил Саша.
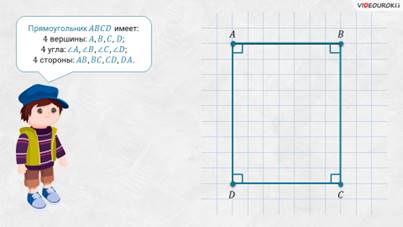
– Всё верно! – подтвердил Электроша. – Посмотрите: стороны AB и BC имеют общую вершину B. Такие стороны называют соседними сторонами прямоугольника ABCD. Также соседними сторонами будут стороны BC и CD с общей вершиной C, CD и DA с общей вершиной D, DA и AB с общей вершиной А.
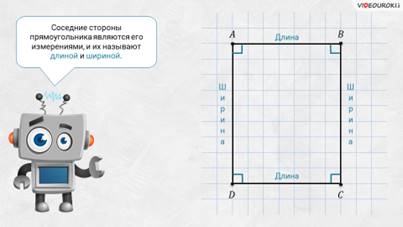
Соседние стороны прямоугольника являются его измерениями, и их называют длиной и шириной.
– А что вы можете сказать о сторонах, например, AB и CD нашего прямоугольника ABCD? – спросил у ребят Электроша.
– Стороны AB и CD не имеют общих вершин, – ответили мальчишки.
– Молодцы! – похвалил ребят Электроша. – Такие стороны называют противолежащими сторонами прямоугольника ABCD. Также противолежащими будут стороны BC и AD. Запомните! Противолежащие стороны прямоугольника равны.
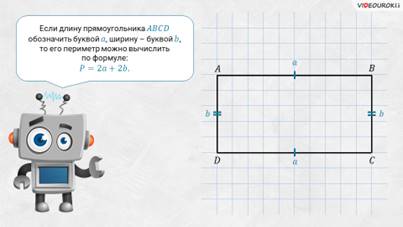
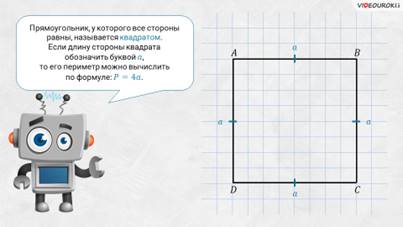
– А теперь посмотрите: на листке изображён прямоугольник ABCD, его противолежащие стороны равны. Если длину прямоугольника обозначить буквой а, а ширину – буквой b, то его периметр можно вычислить по формуле: P = 2a + 2b.
– Среди прямоугольников есть особые, – продолжил Электроша, – у которых все стороны имеют одну и ту же длину. Вы, конечно, помните, что такие прямоугольники называют квадратами. Если длину стороны квадрата обозначить буквой а, то его периметр можно вычислить по формуле: P = 4a.
– А теперь давайте проведём небольшой эксперимент. Возьмите лист бумаги прямоугольной формы и сложите его пополам так, чтобы противолежащие стороны совпали. Затем разверните этот лист. Что вы можете сказать о двух частях, получившихся в результате сгиба листа? – спросил у ребят Электроша.
– Видно, что две части нашего прямоугольного листа, лежащие по разные стороны от линии сгиба, совпадают.
– Молодцы! – похвалил ребят Электроша. – Прямую, которую мы получили в результате сгибания листа, называют осью симметрии.
Запомните! Ось симметрии – это прямая (или воображаемая линия), которая делит геометрическую фигуру на две зеркально одинаковые фигуры. Фигуру, которая имеет ось симметрии, называют симметричной относительно прямой.
– Скажите, сколько осей симметрии имеет прямоугольник? – спросил Электроша.
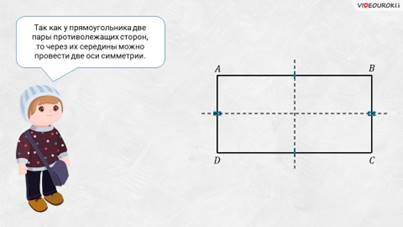
– Так как у прямоугольника 2 пары противолежащих сторон, то через их середины можно провести 2 оси симметрии, – сказал Паша.
– Правильно! А, может, вы ещё сможете привести примеры симметричных фигур в геометрии?
– Например, квадрат, – начал Саша. – У квадрата тоже 2 пары противолежащих сторон, значит, через их середины можно провести 2 оси симметрии.
– Саша, ты чуть-чуть не досчитался! – сказал Электроша. – Вы уже знакомы с таким понятием, как диагональ. Напомню, что диагональ – это отрезок, соединяющий любые две несоседние вершины.
Если лист квадратной формы сложить пополам по диагоналям, то заметим, что и эти пары частей совпадут относительно линий сгиба.
– Значит, у квадрата 4 оси симметрии? – уточнил Саша.
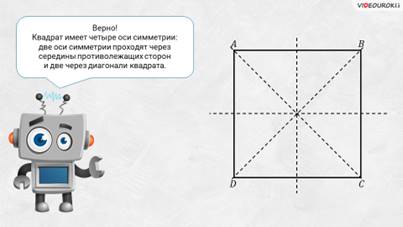
– Верно! – ответил Электроша – Квадрат имеет 4 оси симметрии: 2 оси симметрии проходят через середины противолежащих сторон и 2 – через диагонали квадрата.
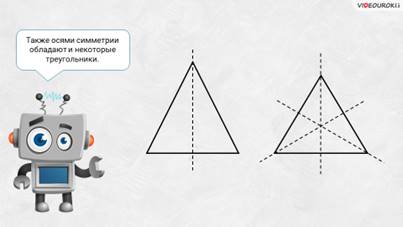
Также осями симметрии обладают и некоторые треугольники. Так, например, в равнобедренном треугольнике можно провести 1 ось симметрии, а в равностороннем – 3.
– С симметрией вы очень часто встречаетесь и в жизни. Люди с давних времён используют симметрию в рисунках, орнаментах, предметах быта, архитектуре, искусстве.
Даже многие буквы нашего алфавита обладают симметрией.
Однако больше всего восхищает симметрия в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, окраске и расположении различных органов животных, в форме кристаллических тел.
В порхающей бабочке и сказочной зимней снежинке.
Объекты, которые обладают осью симметрии, всегда легко воспринимаются и приятны для глаза. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота». Симметрия означает соразмерность, наличие определённого порядка в расположении частей.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
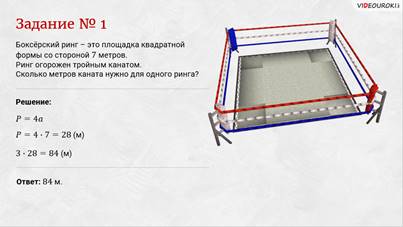
Задание первое: боксёрский ринг – это площадка квадратной формы со стороной 7 м. Ринг огорожен тройным канатом. Сколько метров каната нужно для одного ринга?
Решение: чтобы узнать, сколько понадобится метров каната для ринга, нужно знать периметр ринга. Мы знаем, что ринг имеет форму квадрата со стороной 7 м. Применяя формулу для вычисления периметра квадрата, получаем, что наш ринг имеет периметр 28 м. Так как ринг огорожен тройным канатом, то для одного ринга понадобится 84 метра каната.
Следующее задание: сколько осей симметрии имеет шестиугольник с равными сторонами?
Решение: так как, по условию, шестиугольник имеет равные стороны, а их 6, значит, можно провести 3 оси симметрии через середины противолежащих сторон. Также можно провести ещё 3 оси симметрии через диагонали шестиугольника. Тогда всего получим 6 осей симметрии.
Ось симметрии – это прямая (или воображаемая линия), которая делит геометрическую фигуру на две зеркально одинаковые фигуры.
Фигуру, которая имеет ось симметрии, называют симметричной относительно прямой.
У прямоугольника 2 оси симметрии, у квадрата – 4, у равнобедренного треугольника – 1, а у равностороннего – 3.