Что такое остаток в математике

Деление с остатком. Формула деления с остатком и проверка.

Деление с остатком.

Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.

Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?

Решение:
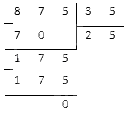
Поделим число 16 на 5 столбиком получим:

Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.

a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.

Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.

Остаток от деления

Остаток всегда должен быть меньше делителя.

Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.

Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.

Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.

Остаток может быть равен делителю?
Ответ: нет.

Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)

Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8

Решение:
а) Делим столбиком:

258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6 Category: 5 класс, Натуральные числа Leave a comment

Источник

Остаток от деления

Остаток от деления в арифметике — один из результатов операции деления с остатком. Образуется, если результат деления не может быть выражен целым числом, при этом остаток от деления должен быть по абсолютной величине меньше делителя. В случае, если числа делятся друг на друга без остатка, или нацело, то считают, что остаток равен нулю. Термин применяется также при делении многочленов.

Содержание

Натуральные числа

Остатком называется неотрицательное число, которое в сумме с произведением неполного частного и делителя даёт делимое. То есть,

если , то , где , то есть при делении на даёт (неполное) частное и остаток .

Остаток от деления a на b можно явно выразить через функцию «пол»:

Обобщения

Целые числа

даёт обобщение понятия остатка на случай деления целого числа a на целое число b. При этом выполняется соотношение и неравенство .

Вещественные числа

Если два числа и (отличное от нуля) относятся к множеству вещественных чисел, может быть поделено на без остатка, при этом частное является также вещественным числом. Если же частное по условию должно быть целым числом, в этом случае остаток будет вещественным числом, то есть может оказаться дробным.

если , то , где

(остаток 1,6)

Многочлены

При делении двух полиномов и степень остаточного полинома должна быть строго меньше степени делителя:

, причём Пример (здесь остатком является свободный член)

См. также

Полезное

Смотреть что такое «Остаток от деления» в других словарях:

остаток (от деления) — — [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ. Москва 1993] Тематики информационные технологии в целом EN remainder … Справочник технического переводчика

остаток целочисленного деления — модуль — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы модуль EN modulo … Справочник технического переводчика

Остаток — Остаток: В математике: Остаток от деления число, образующееся при делении с остатком. Остаток ряда ряд, полученный отбрасыванием n первых членов от исходного ряда. В астрономии: Остаток сверхновой газопылевое образование, результат… … Википедия

БЕЗУ ТЕОРЕМА — остаток от деления многочлена Рn(х) степени п на двучлен х b, где b число, равен Рп(b). Установлена Э. Безу в 1779 … Естествознание. Энциклопедический словарь

Контрольное число — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия

Контрольная цифра — Контрольное число, контрольная цифра разновидность контрольной суммы, добавляется (обычно в конец) длинных номеров с целью первичной проверки их правильности. Применяется с целью уменьшения вероятности ошибки при обработке таких номеров: машинном … Википедия

Контрольное число — Эта статья требует доработки. Вы поможете проекту, исправив и дополнив её. Надо разнести практическую информацию по соответствующим статьям. stas® 01:53, 14 сентября 2009 (MSD) Контрольное число, контрольная цифра разновидность контрольной су … Бухгалтерская энциклопедия

Признак Паскаля — метод, позволяющий получить признаки делимости на любое число. Своего рода «универсальный признак делимости». Содержание 1 Общий вид 2 Доказательство 3 О … Википедия

Пасхалия — собрание правил, на основании которых вычисляется день празднования Пасхи. На основании предписаний, изложенных в книге Исход, а также лунно солнечного календаря, окончательно принятого евреями в эпоху второго храма, еврейская Пасха празднуется… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

АРИФМЕТИКА — искусство вычислений, производимых с положительными действительными числами. Краткая история арифметики. С глубокой древности работа с числами подразделялась на две различные области: одна касалась непосредственно свойств чисел, другая была… … Энциклопедия Кольера

Источник

Деление чисел с остатком

Деление с остатком целых положительных чисел

Деление — это разбиение целого на равные части.

Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.

Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!

Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.

Попрактикуемся в решении.

Пример

Разделить 14671 на 54.

Выполним деление столбиком:

Неполное частное равно 271, остаток — 37.

Ответ: 14671 : 54 = 271(остаток 37).

Деление с остатком положительного числа на целое отрицательное

Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:

В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.

Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.

Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».

Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.

Алгоритм деления положительного числа на целое отрицательное (с остатком):

Пример

Разделить 17 на −5 с остатком.

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.

Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.

Ответ: 17 : (− 5) = −3 (остаток 2).

Деление с остатком целого отрицательного числа на целое положительное

Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:

Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:

d = a − b * c

Из правила делаем вывод, что при делении получается целое неотрицательное число.

Для точности решения применим алгоритм деления а на b с остатком:

Рассмотрим пример, где можно применить алгоритм.

Пример

Найти неполное частное и остаток от деления −17 на 5.

Разделим заданные числа по модулю.

Получаем, что при делении частное равно 3, а остаток 2.

Так как получили 3, противоположное ему −3.

Необходимо отнять единицу: −3 − 1 = −4.

Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:

d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.

Значит, неполным частным от деления является число −4 с остатком 3.

Ответ: (−17) : 5 = −4 (остаток 3).

Деление с остатком целых отрицательных чисел

Сформулируем правило деления с остатком целых отрицательных чисел:

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:

d = a − b * c

Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.

Алгоритм деления с остатком целых отрицательных чисел:

Пример

Найти неполное частное и остаток при делении −17 на −5.

Применим алгоритм для деления с остатком.

Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.

Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.

Получилось, что остаток равен 3, а неполное частное равно 4.

Ответ: (−17) : (−5) = 4 (остаток 3).

Деление с остатком с помощью числового луча

Деление с остатком можно выполнить и на числовом луче.

Пример 1

Рассмотрим выражение: 10 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.

Решение: 10 : 3 = 3 (остаток 1).

Пример 2

Рассмотрим выражение: 11 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.

Решение: 11 : 3 = 3 (остаток 2).

Проверка деления с остатком

Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.

Формула деления с остатком

a = b * c + d,

где a — делимое, b — делитель, c — неполное частное, d — остаток.

Эту формулу можно использовать для проверки деления с остатком.

Пример

Рассмотрим выражение: 15 : 2 = 7 (остаток 1).

В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:

Теорема о делимости целых чисел с остатком

Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.

Теорема

Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:

где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.

Доказательство:

Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.

Тогда необходимо взять q такое, чтобы данное неравенством b * q

Источник

Общее представление о делении натуральных чисел с остатком

В данном материале мы разберем, как разделить одно натуральное число на другое с остатком. Для начала сформируем общее представление о таком действии, определимся с терминами и обозначениями, а потом посмотрим, какие задачи можно решить с его помощью. В последнем пункте попробуем объяснить, какие связи существуют между понятиями делимого, делителя, неполного частного и остатка от деления.

Общее представление о делении с остатком

Разделить с остатком – значит представить исходное множество в виде некоторого числа равных множеств и еще одного дополнительного, элементов которого недостаточно для создания требуемого множества.

В чем состоит смысл деления с остатком?

1) если b –количество элементов в каждом равном множестве, полученном после деления, то c – это количество множеств, которое у нас получилось.

2) если b – это количество множеств, то c – это число предметов в каждом из них.

Основные понятия, используемые при делении с остатком

Здесь мы определимся с основными терминами, которые будем использовать, если речь идет о делении с остатком.

Знак деления, используемый при решении примеров с остатком, аналогичен тому же знаку «разделить» (две точки, расположенные вертикально), что и при делении нацело. В некоторых источниках можно встретить обозначение « ÷ », смысл которого тот же самый. Так, числовое выражение 16 : 3 означает деление одного натурального числа на другое с остатком.

Также можно записать это в виде схемы: делимое: делитель = неполное частное (ост. остаток).

Из самого понятия о делении с остатком следует, что в любом случае остаток будет меньше делителя. Если бы он был равен ему или был нулевым, то это уже было бы деление нацело, поскольку у нас в итоге вышло бы несколько равных множеств.

Задачи, в которых используется деление с остатком

В результате процесса деления, описываемого в этой статье, всегда получаются два числа, одно из которых является остатком, а другое – неполным частным. Поэтому оно будет полезно для решения двух разных типов задач:

1. Нахождение количества необходимых равных множеств, которые можно составить из заданного количества предметов, или же количества предметов в равных множествах, полученных в результате деления.

У нас есть 67 шаров, которыми мы будем наряжать елки. Если на каждую елку нужно 15 шаров, сколько всего елок можно нарядить? Результат мы получим после деления с остатком.

Вычислять мы можем не только количество предметов, но и изменения величин (массы, времени, длины и др.)

Например, на заводе произведено 6 113 л молока. Его нужно разлить в бутылки по 2 л. Мы можем вычислить неполное частное и понять, сколько бутылок будет в итоге. Или же если на производство какого-то изделия тратится 3 часа, то мы можем найти, сколько можно их выпустить за один восьмичасовой рабочий день.

2. Задачи второго типа направлены на вычисление количества предметов в исходном множестве, которые остались после деления. Это могут быть не только предметы, но и величины.

Чтобы изготовить бетонную плиту, надо израсходовать 750 кг цемента. Если мы закупили 12 900 кг, на сколько плит нам хватит? Результат мы вычислим в результате деления с остатком.

Основные связи между понятиями делимого, делителя, неполного частного и остатка от деления

Для установления этих связей сразу разберем конкретный пример.

Если у нас есть значения делителя, неполного частного и остатка, мы можем найти делимое. Если мы объединим все имеющиеся кучки и добавим к ним остаток, то получим множество из исходного количества предметов.

Чтобы найти делимое, нужно сложить остаток с произведением делителя на неполное частное.

Верное равенство, полученное в итоге, будет полезно для решения задач с неизвестным делимым, то есть таких, где нужно найти исходное число предметов. Приведем пример:

Вычислите делимое, если неполное частное равно одиннадцати, остаток двум, а делитель семи.

Решение

Если нам известны значения делимого, делителя и неполного частного, то мы можем найти остаток.

Чтобы найти остаток от деления одного натурального числа на другое, нужно вычесть из делимого произведение делителя на неполное частное.

Решение

Если нужно найти неполное частное, нужно из делимого вычесть остаток и результат разделить на делитель.

Решение

Отнимем остаток от делимого и результат разделим на делитель. Считаем: ( 221 − 13 ) : 52 = 208 : 52 = 4 (для подсчета мы использовали метод подбора частного).

Найти делитель можно, если вычесть из делимого остаток и получившуюся разность разделить на неполное частное.

Возьмем пример решения такой задачи.

Решение

Источник

Mod и остаток — не одно и то же

Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!

Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.

Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.

В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»

Позовите ребят из секты «mod не остаток»! Это для вас.

Что такое mod?

Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.

Вот где мы попадаем в странную серую область.

Математика циферблата

Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.

Впрочем, не будем отклоняться от темы.

Остатки и математика циферблата

Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.

Рассмотрим такую задачу:

JavaScript с этим согласен:

Google согласен с первым утверждением, но не согласен со вторым:

Ruby согласен с Google:

Во имя Дейкстры, что здесь происходит?

Вращение часов назад

Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.

Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:

Это известная вещь

Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:

Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.

Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:

Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.

А как на вашем языке?

Ну и что?

Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:

Источник