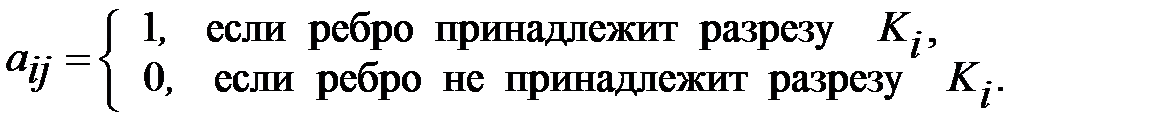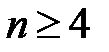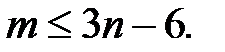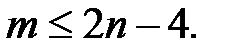Что такое остов графа
Остовы графа
Содержание
Остов графа
Пусть G — произвольный (n, m)-граф с k компонентами связности. Если G — не дерево, то в нем (его компонентах связности) существуют циклы. Рассмотрим какой-либо цикл и удалим из него некоторое ребро. При этом количество компонент связности не увеличится. Если после этого еще останутся циклы, то рассмотрим следующий из них и снова удалим какое-либо его ребро. Продолжим этот процесс до тех пор, пока не исчезнут все циклы. Полученный в результате подграф, который, очевидно, является лесом и имеет столько же компонент связности, как и исходный граф G, называется остовом графа G.
Остовым (покрывающим) деревом графа G называется любое дерево T, являющееся суграфом графа G. Покрывающее дерево T в связном графе определяется неоднозначно.
Связный граф имеет единственное покрывающее дерево тогда и только тогда, когда он сам является деревом.
Остов графа G является минимальным связным суграфом графа G, то есть содержит минимальное количество ребер, связывающих вершины графа.
Суграф T графа G называется каркасом этого графа, если он является лесом, который на любом компоненте связности графа G образует дерево.
Теорема
Число ребер произвольного графа G с n вершинами и m ребрами, имеющего k компонент связности, которое необходимо удалить для получения остова, не зависит от последовательности их удаления и равно m-n+k.
Доказательство теоремы
Определения
Число ν(G)=m-n+k называется цикломатическим числом (циклическим рангом) графа G. Число ν*(G)=n-k, то есть число ребер, входящих в любой остов графа G называется его коциклическим рангом. ν(G)+ν*(G)=m. Корневым деревом называется дерево T=(V,E) с выделенной вершиной ν, принадлежащая V, при этом вершина ν называется корнем дерева. Для каждой вершины корневого дерева её уровень — это длина цепи от корня до этой вершины.
Следствия
Следствие 1 Граф G является лесом тогда и только тогда, когда ν(G)=0.
Следствие 2 Граф G имеет единственный цикл тогда и только тогда, когда ν(G)=1.
Следствие 3 Граф G, в котором число ребер не меньше, чем число вершин, имеет цикл.
Теорема (Кирхгоф)
Число остовов в связном графе G порядка n≥2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа K(G) графа G.
Теорема. Орграф сильно связан, если в нем существует остовной циклический маршрут.
Полезное
Смотреть что такое «Остовы графа» в других словарях:
Семейство полорогие — (Bovidae)** * * Семейство полорогих, или бычьих самая обширная и разнообразная группа парнокопытных, включает 45 50 современных родов и около 130 видов. Полорогие животные составляют естественную, ясно очерченную группу. Как ни… … Жизнь животных
Семейство настоящие лягушки — У семейства настоящих лягушек зубы имеются только на нижней челюсти; поперечные отростки крестцового позвонка имеют цилиндрическую форму, к концу слабо или совсем не расширяясь. Грудной пояс у отдельных родов мало различается, зато форма… … Жизнь животных
Остов графа



Остов – минимальное множество ребер, которые связывают все вершины связного графа.
Остов это дерево. Часть G‘ графа G называется остовом (каркасом, скелетом), если V’ = V и все они связаны без циклов. Остов обычно обозначают буквой T. Для орграфов остов – часть G, которая является остовом в неорграфе, полученном из G удалением ориентации дуг.
Остов получается из графа разрушением циклов. Число удаляемых при этом ребер: 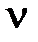
Если граф состоит из нескольких компонент, то его остов лес, а число удаляемых при определении остова ребер будет равно:
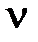
где ρ – количество компонент связности графа.
Количеств ребер в остове графа:
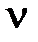
называется коциклическим рангом.
(У связного графа 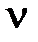
Для дерева цикломатическое число равно 0.
Нахождение остова минимальной длины
3) Повторяем п. 2, пока находятся нужные ребра.
Фундаментальным циклом графа G(V,E) с остовным деревом T(V,E‘) называется простой цикл, получаемый в результате добавления к T одного из ребер G, не принадлежащего E‘. Количество фундаментальных циклов графа G = (V,E) при любом остовном дереве T равно цикломатическому числу 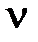
Пусть G(V, E) связный неорграф с n вершинами и m ребрами, T – остов графа, имеющий n – 1 ребро, которые называются ветвями T (ведь остов – это дерево) и обозначаются bj.
Не входящие в остов 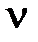
Если к дереву T добавить произвольную хорду hi, то образуется точно один цикл Ci. Этот цикл состоит из хорды hi и некоторых ветвей остова, образующих простую цепь и соединяющих вершины хорды hi.
Цикл Ci называется фундаментальным циклом графа G относительно хорды hi остова T (в общем случае остовов в графе может быть много). Таким образом, фундаментальный цикл содержит точно одну хорду остова графа.
Множество всех фундаментальных циклов <C1, C2, …, Ci, …, Cm–n+1> относительно хорд остова T называется фундаментальным множеством циклов графа G. Мощность этого множества равна цикломатическому числу 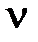
фундаментальное множество циклов графа можно задать с помощью матрицы, строки которой имеют вид
где hi, bj – хорды и ветви соответственно.
В каждом цикле имеется одна хорда hi и некоторое множество ветвей остова T. Этой хорде hi и ветвям, входящим в цикл Ci, присвоим значение 1, остальным ребрам графа присвоим значение 0. Повторяя процедуру для всех хорд, получим матрицу строк из 0 и 1.
Разрезом неорграфа G(V,E) по разбиению множества вершин V на два подмножества V1 и V2 называется множество ребер, соединяющих вершины из подмножества V1 с вершинами подмножества V2. В связном графе любой разрез не пуст.
Непустой разрез K неорграфа G называется простым или коциклом, если множество ребер K не содержит разрезов G ни по какому разбиению (любой разрез разбивает граф на две части – увеличивает число компонент связности).
В связном неорграфе остов T имеет, по крайней мере, одно общее ребро с любым разрезом графа.
В связном неорграфе любой цикл имеет с любым разрезом, проходящим через ребра цикла, четное число ребер.
Удаляя произвольную ветвь bi из T, получаем лес с двумя компонентами, т. е. каждое ребро bi есть разрез T по некоторому разбиению вершин V1, V2.
Множество ребер Ki = <bi, hi1, …, hij> образует разрез G относительно ветви bi, который называют фундаментальным разрезом относительно bi остова T. Таким образом, фундаментальный разрез содержит точно одну ветвь остова графа.
Множество <K1, K2, …, Kn–1> всех фундаментальных разрезов графа G называется фундаментальным множеством разрезов графа G относительно остова T.
Мощность этого множества равна 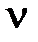
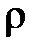
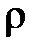
По аналогии с фундаментальными циклами, каждому фундаментальному разрезу можно поставить в соответствие вектор
где
Из этих векторов можно составить матрицу фундаментальных разрезов.
Поскольку каждый фундаментальный разрез содержит точно одну ветвь T, то матрица K имеет вид:
| hi,j – хорды | bi – ветви T | |||||||
| K1 | h1,1 | . | h1,V* | . | ||||
| K = | . | h2,1 | . | h2,V* | . | |||
| . | . | . | . | . | . | . | . | . |
| KV* | hV*,1 | . | hV*,V* | . |
где v* это 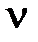
Таким образом 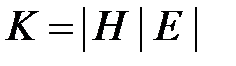
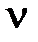
Матрицы фундаментальных циклов C и фундаментальных разрезов K взаимосвязаны.
Если 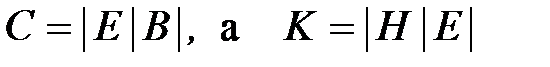
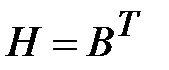
где 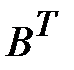
Следовательно, для анализа графа достаточно найти одну матрицу (C или K), а другую можно определить транспонированием.
Планарные графы
Планарный граф – это граф, допускающий укладку на плоскости, т.е. он может быть изображен на плоскости так, что никакие ребра не имеют общих точек, кроме своих вершин. Изображение графа на плоскости с соблюдением этого условия называется плоским графом.
Планарность нужна, например, для реализации печатного монтажа, в процессе разработки которого схема устройства представляется в виде графа: элементы – вершины, связи между выводами элементов – ребра.
Если граф не планарен, то приходится удалять (переносить на другой слой, на другую плоскость) отдельные ребра. Минимальное число ребер, которое надо удалить для получения плоского изображения, называется числом планарности графа и обозначается 

Из формулы следует, что при n = 4 

При перенесении на вторую плоскость, перенесенная часть может опять оказаться не плоской. Тогда отдельные ребра переносят на новую плоскость и т.д. Минимальное число плоскостей, при котором граф разбивается на плоские части, называется толщиной графа и обозначается t(G).
Толщина произвольного графа удовлетворяет неравенству
t(G) 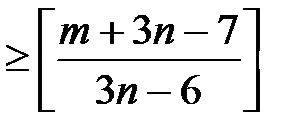
Здесь [x] – целая часть x.
Толщина полных графов удовлетворяет неравенству
t(Kn) 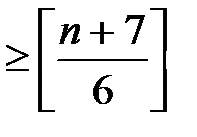
Ответ на первый вопрос: – Граф планарен? – можно получить, если воспользоваться условиями планарности.
У связного плоского графа с n 
У связного плоского двудольного графа
У плоского графа кроме вершин и ребер можно выделить еще один геометрический образ – грань. Область плоскости, ограниченная ребрами связного плоского графа и не содержащая внутри себя ни ребер, ни вершин, называется его гранью. Внешняя неограниченная грань называется бесконечной гранью. У графа без циклов ровно одна грань – бесконечная. Не следует думать, что она какая–то исключительная. При укладке графа на сферу эта грань ничем не будет отличаться от других.
Число граней f в связном плоском графе определяется из соотношения:
где n – число вершин, m – число ребер.
Будем называть кускомграфа G относительно G1:
1) ребро 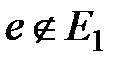
Алгоритм использует последовательный процесс присоединения к некоторому плоскому подграфу 
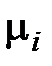


В качестве начального плоского графа 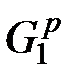

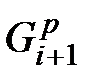


Для каждого куска определяем грани, которые с ним совместимы. Возможны три случая:
1) Некоторый кусок не совместим ни с какой гранью графа 
2) Какой–либо кусок совместим с единственной гранью fk графа 
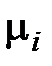


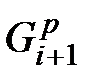
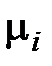
3) Если каждый из кусков Рj совместим, по крайней мере, с двумя гранями графа 
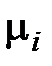
Деревья, их характеризации. Остов графа.
Дерево — это связный ациклический граф (то есть граф, не содержащий циклов, между любой парой вершин которого существует ровно один путь).[1]
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.[2]
Дерево не имеет кратных рёбер и петель.
Любое дерево с n вершинами содержит n − 1 ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда B − P = 1, где B — число вершин, P — число рёбер графа.
Граф является деревом тогда и только тогда, когда любые две различные его вершины можно соединить единственным элементарным путём.
Любое дерево однозначно определяется расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами.
Любое дерево является двудольным графом. Любое дерево, содержащее счётное количество вершин, является планарным графом.
Для любых трех вершин дерева, пути между парами этих вершин имеют ровно одну общую вершину.
Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.
Билет 16
Булевы решётки
Булева алгебра, булева решётка — частично упорядоченное множество специального вида; дистрибутивная решётка, имеющая наибольший элемент 1 — единицу булевой алгебры, наименьший элемент 0 — нуль булевой алгебры, и содержащая единственное дополнение каждого своего элемента x — элемент (не x)
Билет 16
Полные графы. Дополнение графа. Полные подграфы. Теорема Рамсея.
Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с n вершинами имеет n(n − 1) / 2
В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они не смежны в G. Чтобы найти обратный граф, дополните данный граф до полного и удалите все ребра, которые уже были до этого.
Пусть даны числа a1,a2. an. Тогда существует такое число R, что, как бы мы ни покрасили рёбра полного графа на R вершинах в n цветов, найдётся либо полный подграф 1-го цвета на a1 вершинах, либо полный подграф 2-го цвета на a2 вершинах, … либо полный подграф n-го цвета на an вершинах.
Билет 17
Булево кольцо
Булевым кольцом называют кольцо, в котором все элементы идемпотентны (коммутативность, наличие единицы или делителей нуля не требуется). Интересной особенностью булевых колец является то, что
в частности, при
то есть булево кольцо всегда коммутативно.
Билет 17
Двудольные графы, необходимое и достаточное условие существования.
Двудо́льный граф или бигра́ф — это математический термин теории графов, обозначающий граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.
Граф является двудольным тогда и только тогда, когда он не содержит цикла нечётной длины. Поэтому двудольный граф не может содержать клику размером более 2.
Граф является двудольным тогда и только тогда, когда он 2-раскрашиваем (то есть его хроматическое число равняется двум)
Граф разбивается на пары разноцветных вершин тогда и только тогда, когда любые k элементов одной из долей связаны по крайней мере с k элементами другой (Теорема Холла).
Двудольный граф, у которого в каждой части больше 2 вершин, является непланарным.
Билет 20
Решетки. Группы. Унарные алгебры.