Что такое отношение в информатике
Разнообразие отношений объектов и их множеств. Отношения между множествами
Урок 4. Информатика 6 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Разнообразие отношений объектов и их множеств. Отношения между множествами»
· отношения между множествами.
Итак, на первом уроке мы узнали, что такое объект и какие отличительные признаки он имеет. Объект также можно охарактеризовать с помощью отношений, в которых этот объект находится с другими объектами.
Подробнее разберём на примерах.
Антон сын Юрия. Эйфелева башня находится в Париже. Кислород входит в состав воды.
Москва – столица России (является столицей). Антон дружит с Аней.
В данных примерах выделено имя отношения, которое обозначает характер связи между ними.
Таким образом, отношение – это взаимосвязь между объектами.
Одинаковыми отношениями могут быть связаны одновременно несколько объектов.
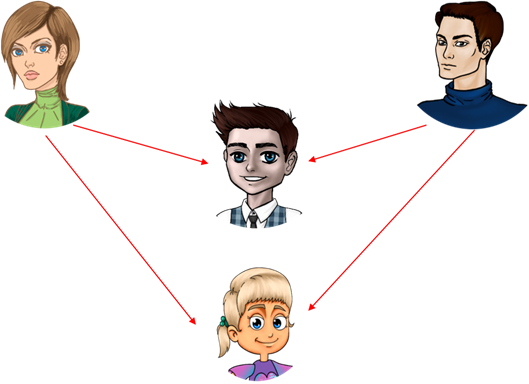
ученик Антон решил составить генеалогическое дерево своей семьи.
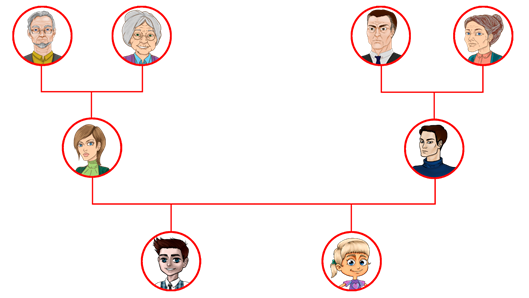
Для этого ему необходимо было узнать, кто в каких отношениях находится. То есть он приходится сыном своего отца (Юрия) и мамы (Татьяны). В свою очередь Татьяна приходится дочерью Леонида (дедушка Антона) и Елены (бабушка Антона). Юрий приходится сыном Григория (дедушка Антона) и Марии (бабушка Антона). Так же у Антона есть сестра Маша. Так как словесное восприятие вызывает затруднение, давайте поможем Антону представить это все в виде схемы и постоим генеалогическое дерево.
Видим, что самыми старшими являются дедушки и бабушки Антона, поэтому расположим их в самом верху.
У Леонида и Елены есть дочь Татьяна, а у Григория и Марии сын Юрий. Значит, разместим их на втором уровне (если считать сверху) и укажем их отношения с родителями в виде стрелок.
У Татьяны и Юрия есть сын Антон и дочь Маша. Разместим их аналогичным образом на нашей схеме.
На данной схеме стрелками указаны отношения, то есть сверху вниз стрелка обозначает, что тот, кто находится выше – приходится отцом или матерью, а тот, кто ниже – приходится сыном или дочерью. В данном случае можно обойтись и без стрелок. Получим следующую схему.
Таким образом, мы узнали, как же можно схематически показать отношение между объектами.
Следует запомнить, что такими отношениями могут быть связаны только объекты некоторых видов. А в отношениях «является элементом множества», «входит в состав» и «является разновидностью» могут находиться любые объекты.
Подходя к рассмотрению отношений множеств, разберём несколько примеров.
Для начала рассмотрим, как отношения связывают два множества.
помидоры – это овощи (являются элементом множества);
тигры относятся к семейству кошачьих;
10 входит в состав двухзначных чисел.
Для графического представления множеств удобнее использовать круги Эйлера.
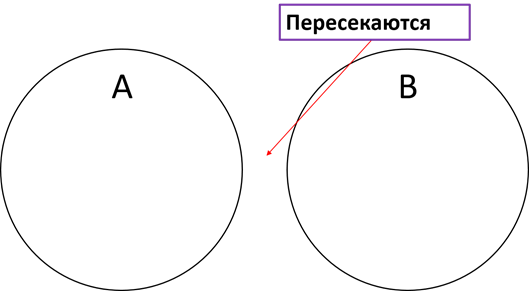
Существует два каких-то множества A и B (изобразим в виде двух кругов). Итак, если множества имеют общие элементы, то есть элементы одновременно принадлежат и множеству A, и множеству B, то эти множества пересекаются.
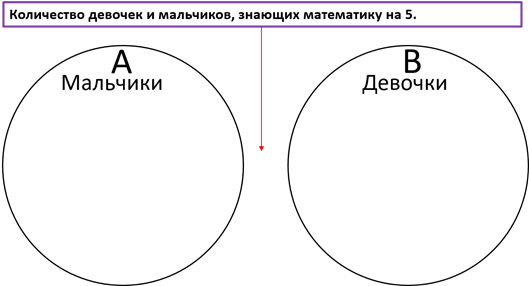
Например, Антон учится в 6 «А» классе. В классе восемнадцать человек: 8 мальчиков и 10 девочек.
У трёх девочек и у троих мальчиков по математике оценка пять. Учительница по математике попросила девочек и мальчиков, которые знают математику на пять сесть на средний ряд.
Для решения этого примера изобразим графически два множества: A – множество мальчиков, B – множество девочек. Так, как и в одном и во втором множестве есть ученики, которые знают математику на пять – объединим их и получим следующее.
Пересечением множеств и является количество девочек и мальчиков, знающих математику на пять, то есть это те учащиеся, которые сели на средний ряд.
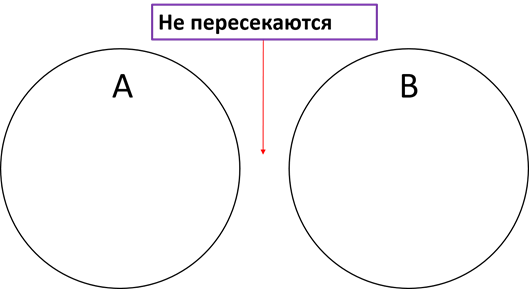
Множества, не имеющие общих элементов, не пересекаются.
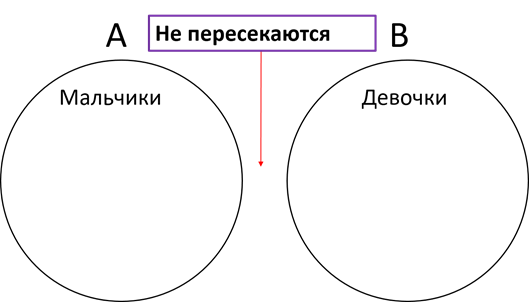
Разберём все тот же пример. В классе у Антона восемнадцать человек: восемь мальчиков и десять девочек. Возьмём A – множество мальчиков, B – множество девочек. Так как ничего общего, указанного в данном примере, между этими двумя множествами нет, то они не пересекаются.
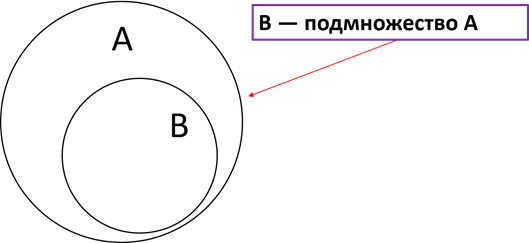
Если каждый элемент множества B является элементом множества A, то B является подмножеством A.
И снова возвращаемся к примеру, с классом Антона. Антон учится в 6 «А» классе. В классе восемнадцать человек. В школе учатся четыре шестых класса. Пусть A – множество параллели шестых классов, B – множество 6 «А» класса. Таким образом, каждый учащийся 6 «А» класса также является учащимся параллели шестых классов. То есть множество B является подмножеством A.
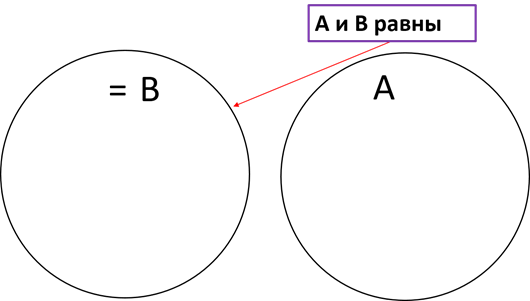
Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то множества А и В равны.
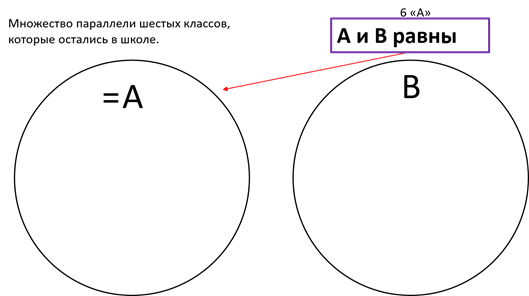
Например, Антон учится в 6 «А» классе. В школе учатся четыре шестых класса – 6 «А», 6 «Б», 6 «В», 6 «Г». Три из четырёх классов – 6 «Б», 6 «В» и 6 «Г» отправились на экскурсию и в школе из всей параллели 6-х классов остался один 6 «А». Итак, пусть A – множество параллели шестых классов, которые остались в школе, B – множество 6 «А» класса. Таким образом, каждый учащийся 6 «А» класса также является учащимся параллели шестых классов, которые остались в школе. То есть множество B равно множеству A.
Отношение – это взаимосвязь между объектами.
Если два множества имеют общие элементы, т.е. элементы одновременно принадлежат и первому и второму множеству, то эти множества пересекаются.
Множества, не имеющие общих элементов, не пересекаются.
Если каждый элемент множества B является элементом множества A, то B является подмножеством A.
Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то множества А и В равны.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 3. Отношения объектов и их множеств
Информатика. 6 класса. Босова Л.Л. Оглавление
Ключевые слова:
Разнообразие отношений.
Человек может рассказать не только о признаках объекта, но и об отношениях, в которых этот объект находится с другими объектами. Например:
В каждом из приведённых предложений выделено имя отношения, которое обозначает характер связи между двумя объектами.
Отношение — это взаимная связь, в которой находятся какие-либо объекты.
Одним и тем же отношением могут быть попарно связаны несколько объектов. Соответствующее словесное описание может оказаться очень длинным, и тогда в нём трудно разобраться.
Пусть про населённые пункты А, Б, В, Г, Д и Е известно, что некоторые из них соединены железной дорогой: населённый пункт А соединён железной дорогой с населёнными пунктами В, Г и Е, населённый пункт Е — с населёнными пунктами А, В, Г и Д.
Для большей наглядности имеющиеся связи («соединён железной дорогой») можно изобразить линиями на схеме отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д. (рис. 4).
Имена некоторых отношений изменяются, когда меняются местами имена объектов, например: «выше» — «ниже», «приходится отцом» — «приходится сыном». В этом случае направление отношения на схеме отношений обозначают стрелкой.
Так, на рис. 4 каждая стрелка направлена от отца к его сыну и поэтому отражает отношение «приходится отцом», а не «приходится сыном». Например: «Андрей приходится отцом Ивану».
Стрелки можно не использовать, если удаётся сформулировать и соблюсти правило взаимного расположения объектов на схеме. Например, если на рис. 5 имена детей всегда располагать ниже имени их отца, то можно обойтись без стрелок.
Такие отношения, как «приходится сыном», «соединён железной дорогой», «покупает», «лечит» и т. д., могут связывать только объекты некоторых видов. В отношениях «является элементом множества», «входит в состав» и «является разновидностью» могут находиться любые объекты.
Отношения могут существовать не только между двумя объектами, но и между объектом и множеством объектов, например:
В каждом из этих предложений описано отношение «является элементом множества».
Отношения между множествами
Отношения могут связывать два множества объектов, например:
Графически множества удобно представлять с помощью кругов, которые называют кругами Эйлера.
Если множества А и В имеют общие элементы, т. е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются (рис. 6).
Пример. Пусть А — множество электронных писем, В — множество писем на русском языке. В пересечение этих множеств попадают все электронные письма на русском языке.
Если множества не имеют общих элементов, то говорят, что они не пересекаются (рис. 7).
Пример. Пусть А — множество компьютерных устройств ввода информации, В — множество устройств вывода информации. Эти множества не имеют общих элементов.
Если каждый элемент множества В является элементом множества А, то говорят, что В — подмножество А (рис. 8).
Пример. Пусть А — множество учеников, В — множество шестиклассников. Множество шестиклассников является подмножеством множества учеников.
Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны (рис. 9).
Пример. Пусть А — множество равносторонних прямоугольников, В — множество квадратов. Эти множества равны.
Отношение «входит в состав»
В зависимости от ситуации объект может либо рассматриваться как единое целое, либо «распадаться» на более мелкие объекты. Например, компьютер рассматривается как единое целое, если нужно подсчитать количество компьютеров в школе. Чтобы получить представление о возможностях компьютера, необходимо рассмотреть характеристики таких его устройств, как процессор, память, жёсткий диск и т. д.
Объект может состоять из множества одинаковых (однородных, подобных) объектов. Например, объект «апельсин» состоит из частей — долек апельсина. Объект «школьный класс» состоит из множества учеников — мальчиков и девочек приблизительно одного возраста. Каждый ученик является целой, самостоятельной частью объекта «школьный класс».
Объект может состоять из множества различных объектов. Например, объект «компьютер» состоит из множества не похожих друг на друга объектов (системный блок, монитор, клавиатура и т. д.). При делении объекта «компьютер» на части новые объекты получают разные имена; признаки новых объектов различны.
При описании состава объектов в одних случаях речь идет о составе конкретного объекта, а в других — об общих составных частях множества объектов. В последнем случае описание состава содержит ответ на вопрос «Из чего обычно состоят объекты некоторого множества?». Например:
Описывая состав объекта, человек мысленно «разбирает» его на части. При этом, как правило, используют такой приём: сначала называют небольшое число крупных частей, затем каждую из них «разбирают» на части поменьше и т. д. Например, при описании состава дома удобно выделить сначала фундамент, стены и крышу, затем в составе стены выделить окно и дверь, затем сообщить, что окно состоит из рамы и стёкол, и так же поступить, описывая состав двери (рис. 10).
Схема отношений «входит в состав» (схема состава) отражает не только составные части, но и тот порядок, в котором предмет «разбирался» на части. Таким образом, она отражает строение (структуру) объекта. На схеме состава можно использовать линии без стрелок, если имя объекта-части располагать ниже имени объекта, которому принадлежит эта часть.
Все имена на рис. 11 — общие (обозначают множества предметов), потому что эта схема отражает состав не одного конкретного дома, а «дома вообще».
При описании признаков сложного, составного объекта человек может назвать не только действия и характеристики всего объекта, но также действия и свойства объектов-частей. Например, весь дом можно строить и ремонтировать, крышу — красить, а стекло — вставлять; весь дом имеет длину, ширину и высоту, стены — толщину, крыша — высоту.
Самое главное
В сообщении об объекте могут быть приведены не только признаки данного объекта, но и отношения, которые связывают его с другими объектами. Имя отношения обозначает характер этой связи. Отношения могут связывать не только два объекта, но и объект с множеством объектов или два множества.
В зависимости от ситуации объект может рассматриваться как единое целое либо «распадаться» на более мелкие объекты.
Объект может состоять из множества одинаковых (однородных, подобных) объектов или множества различных объектов.
Схема отношений «входит в состав» (схема состава) отражает не только составные части, но и тот порядок, в котором предмет «разбирался» на части.
Отношения между объектами
Урок 5. Информатика 4 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Отношения между объектами»
На прошлом занятии мы вспомнили, что объект – это общее название любого предмета, живого существа, явления, процесса, события, если мы обратили на него наше внимание. Также поговорили о том, что каждый объект имеет имена (общее, конкретное и собственное) и свойства (существенные и несущественные, общие и отличительные).
Предлагаю продолжить изучение данной темы по следующему плану.
Вспомнить, что объекты находятся в отношениях между собой и эти отношения имеют свои имена.
Научиться видеть и называть отношения, а также строить схему отношений между двумя объектами.
Все объекты взаимодействуют между собой, то есть находятся в определённых отношениях. Обычно говорят: объекты связаны отношениями.
Отношения имеют свои имена: «меньше», «больше», «дороже», «дешевле», «сильнее», «крупнее», «быстрее», «левее», «шире», «выше», «старше», «младше». Ой, приводить примеры имён отношений можно бесконечно.
Люди могут быть связаны друг с другом родственными отношениями: «брат», «сестра», «бабушка», «мать», «отец», «внучка», «сын», «дядя» и другие.
Бывают производственные отношения: «начальник», «подчинённый», «помощник», «учитель», «ученик» и так далее.
Значит, мы смело может заявлять, что все объекты связаны друг с другом разными отношениями. Обычно это не одно, а много разных отношений.
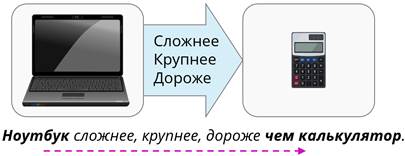
Например, вот 2 объекта: ноутбук и калькулятор. Ноутбук сложнее, крупнее, дороже калькулятора.
Отношения между объектами удобно представлять в виде схемы. Например, отношения между ноутбуком и калькулятором в виде схемы будут выглядеть вот так. Обратите внимание, в сторону какого объекта указывает стрелка.
Мы говорим, что ноутбук сложнее, крупнее, дороже чем калькулятор. Значит стрелка идёт от ноутбука к калькулятору. Если мы стрелку изобразим справа налево, то получится, что калькулятор сложнее, крупнее, дороже ноутбука. А это совсем не так. Отношения в данной схеме будут следующие:
проще, мельче, дешевле.
Думаю, здесь ничего сложного для вас нет, но потренироваться стоит.
Вот перед вами несколько объектов и отношений между ними. Изобразите эти отношения в виде схемы.
А теперь проверьте, так ли у вас получилось.
Если у вас так, эти аплодисменты вам. Идём дальше.
Все отношения между объектами делятся на симметричные и несимметричные.
В симметричных отношениях объект А находится с объектом Б в таких же отношениях, как и объект Б с объектом А.
Например, фехтовальщик слева соперник фехтовальщику справа. И наоборот, фехтовальщик справа соперник фехтовальщику слева.
Максим ровесник Наташи и Наташа ровесница Максима.
Шарик друг Денису, и Денис друг Шарику.
Обратите внимание, что в симметричных отношениях между объектами стрелка двусторонняя.
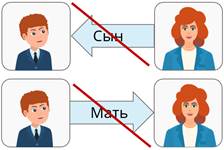
Семейные отношения между братом и сестрой, отцом и сыном, отцом и дочерью, сыном и матерью – это примеры несимметричных отношений. Только не путайте, пожалуйста, направления стрелок. Чтобы случайно у вас не получилось, что женщина – сын мальчика, а мальчик – мать этой женщины.
А вот, например, отношение «сестра» между двумя девочками, конечно симметричное.
К несимметричным отношениям ещё относится такой важный вид отношений как «часть – целое» и «целое – часть».
Например, компьютер – это целое по отношению к его части – монитору.
А вот системный блок – это часть целого – компьютера.
Солнечная система – целое по отношению к планете Земля, которая является её частью.
А планета Земля – часть Солнечной системы.
Ещё в отношениях «часть – целое» и «целое – часть» находятся, например, объекты ветка и дерево, тетрадь и лист, буква и слово, предложение и слово.
Ну, вот ребята, это всё, о чём я хотел рассказать вам сегодня по теме «Отношения между объектами».
Но чувствую, что закрепить полученные знания несколькими заданиями всё же надо.
Итак, первое задание.
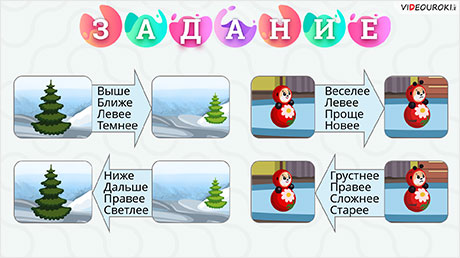
Отметьте подходящие пары отношений между объектами.
Давайте проверим то, что у вас получилось.
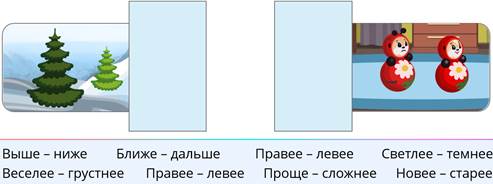
Для объектов слева – ёлок, подходят следующие пары отношений из предложенных: выше-ниже, ближе-дальше, правее-левее, светлее-темнее.
Для объектов «неваляшки» подходят следующие пары отношений из предложенных:
веселее-грустнее, правее-левее тоже подходит, как и для предыдущей пары объектов, проще-сложнее, новее-старее.
Кстати, можете ещё подумать и придумать несколько пар отношений между изображёнными объектами.
А теперь предлагаю представить в виде схем отношения между этими объектами.
Надеюсь, у вас так получилось.
Ну а сейчас, ребята, ещё одно задание.
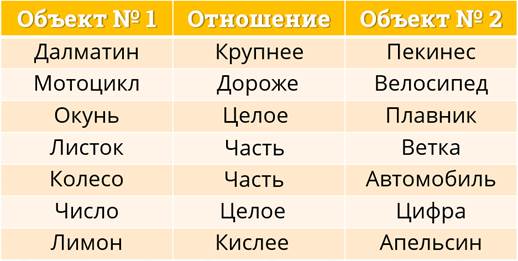
Перед вами таблица. В первом столбике объект номер один, в третьем – объект номер два. А во втором столбике нам необходимо вставить подходящее из этого списка отношение между объектами один и два.
Итак, что же должно было получиться.
Далматин и пекинес. Отношение «крупнее». Да, это действительно так.
Мотоцикл и велосипед. Отношение «дороже».
Окунь – плавник. Отношение «целое».
Листок – ветка. Часть.
Колесо – автомобиль – тоже отношение «часть».
Число – цифра. Отношение «целое».
И последняя пара объектов – «лимон-апельсин». Отношение «кислее».
Вот и подошла к концу наша встреча. Осталось сделать выводы и отметить главное.
Каждый объект связан с другими объектами разными отношениями.
Отношения между объектами имеют имена («больше», «дороже», «уже», «сильнее», «шире», «светлее» и так далее).
Отношения бывают разными: характеризующими вес, размер, расстояние между объектами.
Отношения бывают симметричными и несимметричными.
Важный вид несимметричных отношений – это «часть – целое» и «целое – часть».