Что такое оценка параметра

Понятие оценки параметров

Сформулируем задачу оценки параметров в общем виде. Пусть распределение признака X — генеральной совокупности — задается функцией вероятностей (p(x_/? 0) = Р(Х = х,) (для дискретной случайной величины X) или плотностью вероятности ср(х, б) (для непрерывной случайной величины X), которая содержит неизвестный параметр 9. Например, это параметр X в распределении Пуассона или параметры а и а 2 для нормального закона распределения и т.д.

Для вычисления параметра 0 исследовать все элементы генеральной совокупности не представляется возможным. Поэтому о параметре 9 пытаются судить по выборке, состоящей из значений (вариантов) х _<ух₂, х_п. Эти значения можно рассматривать как частные значения (реализации) п независимых случайных величин X_if Х₂, Х_п, каждая из которых имеет тот же закон распределения, что и сама случайная величина X.

Определение. Оценкой 0„ параметра 0 называют всякую

статистику), с помощью которой судят о значении параметра 0:

Поскольку Х_<, Х₂. Х_п — случайные величины, то и оценка 0„ (в отличие от оцениваемого параметра 0 — величины неслучайной, детерминированной) является случайной величиной, зависящей от закона распределения случайной величины X и числа п.

Назвать «наилучшей» оценкой такую, которая наиболее близка к истинному значению оцениваемого параметра, невозможно, так как выше отмечено, что 0_/7 — случайная величина, поэтому невозможно предсказать индивидуальное значение оценки в данном частном случае. Так что о качестве оценки следует судить не по индивидуальным ее значениям, а лишь по распределению ее значений в большой сети испытаний, т.е. по выборочному распределению оценки. Если значения оценки 0_Я концентрируются около истинного значения параметра 0, т.е. основная часть массы выборочного распределения оценки сосредоточена в малой окрестности оцениваемого параметра 0, то с большой вероятностью можно считать, что оценка 0„ отличается от параметра 0 лишь на малую величину. Поэтому, чтобы значение 0„ было близко к 0, надо, очевидно, потребовать, чтобы рассеяние случайной величины 0_/7 относительно 0, выражаемое, например, математическим ожиданием квадрата отклонения оценки от оцениваемого пара- 2

Определение. Оценка 0_/? параметра 0 называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е.

В противном случае оценка называется смещенной.

Если это равенство не выполняется, то оценка 0„, полученная по разным выборкам, будет в среднем либо завышать значение 0 (если М(0„)>0), либо занижать его (если М(0„) ОО

Определение. Оценка 0₇₇ параметра 0 называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:

или

В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки. Если оценка состоятельна, то практически достоверно, что при достаточно большом п 0„ % 0.

ственно вытекает из неравенства Чебышева:

Так, например, выборочная средняя х является несмещенной и состо- ятельной оценкой генеральной средней х₀ (дисперсия —>0 при/?—» оо,

Определение. Несмещенная оценка 0„ параметра 0 называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра 0, вычисленных по выборкам одного и того же объема п.

Эффективность оценки 0„ определяют отношением

где а? и а? — соответственно дисперсии эффективной и данной оценок.

На практике в целях упрощения расчетов используются оценки, не обладающие высокой эффективностью. Так, например, генеральную среднюю х₀ часто оценивают медианой Me выборки, в то время как эффективной оценкой х₀ является выборочная средняя х (параграф 9.5). При нормальном распределении признака в генеральной совокупности можно показать, что асимптотическая эффективность этой оценки, т.е. е(Ме) = 2/я = 0,64 при п —»со. Это означает, что для получения той же точности и надежности оценки генеральной средней по выборочной средней нужно использовать лишь 64% объема выборки, взятого при оценке по медиане.

Если при тех же условиях для оценки генеральной средней х₀ использовать статистику 0_/z = (x_min +x_max)/2, то (см., например, [231) ее эффек- 24 In я

—-— с ростом п стремится к нулю, и относительно п 2 п

приемлемый результат оценивания (по сравнению с эффективной оценкой х) возможен при малом объеме выборки.

Источник

Понятие оценки параметров.

Проблемы статистических выводов традиционно делятся на проблемы оценивания и проверку гипотез. Главное различие между этими двумя проблемами состоит в том, что при оценивании мы должны определить величину параметра или нескольких параметров. В то время как при проверке гипотез мы должны решить: принять или отвергнуть специфическую величину (или ряд специфических величин) параметра или нескольких параметров.

В общем виде задача оценки параметров формулируется следующим образом.

1. Оценка θ_n параметра θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. M(θ_n) = θ.

В противном случае оценка называется смещенной. Если это равенство не выполняется, то оценка θ_n, полученная по разным выборкам, будет либо завышать θ, если M(θ_n) > θ, либо занижать его, если M(θ_n) 2 есть дисперсия 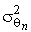, то эффективность является решающим свойством, определяющим качество оценки.

В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности.

4. Оценка θ_n параметра θ является достаточной, если при заданном ее значении распределение наблюдения Х не зависит от параметра θ. Иначе, оценка θ_n обеспечивает оценку параметра без потери информации, содержащейся в выборке.

Однако на практике не всегда оценки удовлетворяют всем трем требованиям. Может оказаться, что даже если эффективная оценка существует, то формулы для ее вычисления оказываются слишком сложными, и тогда используют оценку, дисперсия которой несколько больше. Иногда, в интересах простоты расчетов, применяются незначительно смещенные оценки. Выбору оценки всегда должно предшествовать ее критическое рассмотрение.

Источник

оценивание (параметра)

2.49. оценивание (параметра)

Операция определения на основе выборочных данных числовых значений параметров распределения, принятого в качестве статистической модели генеральной совокупности, из которой извлечена выборка.

Смотреть что такое «оценивание (параметра)» в других словарях:

оценивание параметра — parametro įvertinimas statusas T sritis automatika atitikmenys: angl. parameter estimation vok. Parameterschätzung, f rus. оценивание параметра, n pranc. estimation du paramètre, f … Automatikos terminų žodynas

Интервальное (доверительное) оценивание параметра — получение оценки параметра в виде доверительного интервала. Источник … Словарь-справочник терминов нормативно-технической документации

Точечное оценивание параметра — получение оценки параметра в виде одного численного значения. Источник … Словарь-справочник терминов нормативно-технической документации

оценивание — 4.12 оценивание (evaluation): Систематическое определение степени, с которой некоторый объект удовлетворяет установленным критериям. Источник: ГОСТ Р ИСО/ … Словарь-справочник терминов нормативно-технической документации

ОЦЕНИВАНИЕ СТАТИСТИЧЕСКОЕ — один из основных разделов статистики математич. (см.), посвященный оцениванию по случайным наблюдениям тех или иных характеристик из распределения. В социологич. исследованиях чаще всего используются два вида О.с. точечное и интервальное.… … Российская социологическая энциклопедия

СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — один из осн. разделов матем. статистики … Физическая энциклопедия

ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ — способ получения оценки для неизвестного значения скалярного параметра с помощью интервала его допустимых значений и определения вероятности того, что в этом интервале находится истинное значение параметра. На практике для получения интервальной… … Физическая энциклопедия

Кластерное оценивание — Кластерное оценивание оценка программ совместно работающих структур, объединенных для повышения качества работы, упрощения взаимодействия, привлечения новых идей. В последнее время активно развиваются такие экономические объединения, как… … Википедия

Источник

оценка параметра

Смотреть что такое «оценка параметра» в других словарях:

Оценка (значения) — Оценка (в философии) способ установления значимости чего либо для действующего и познающего субъекта. Оценка (педагогика) выраженное в числе мнение преподавателя (другого проверяющего лица) об уровне знаний ученика (качестве его работы) Оценка (в … Википедия

оценка телеметрируемого параметра — Значение параметра или функциональная зависимость его от времени или другого аргумента, полученные по результатам обработки телеметрических сообщений. Примечание Оценка может отличаться от истинного значения наличием внесенных погрешностей. [ГОСТ … Справочник технического переводчика

Оценка (значение) — Оценка (метрология) в метрологии, приближённое значение величины или параметра, найденное по экспериментальным данным Оценка (философия) способ установления значимости чего либо для действующего и познающего субъекта. Оценка (экономика) процесс… … Википедия

Оценка — (метрология) в метрологии, приближённое значение величины или параметра, найденное по экспериментальным данным Оценка (философия) способ установления значимости чего либо для действующего и познающего субъекта. Оценка (экономика) процесс… … Википедия

ОЦЕНКА СТАТИСТИЧЕСКАЯ — функция от случайных величин, применяемая для оценки неизвестных параметров теоретич. распределения вероятностей. Методы теории О. с. служат основой современной теории ошибок; обычно в качестве неизвестных параметров выступают измеряемые физич.… … Математическая энциклопедия

оценка — 3.9 оценка (evaluation): Систематическое определение степени соответствия объекта установленным критериям. Источник: ГОСТ Р ИСО/МЭК 12207 99: Информационная технология. Процессы жизненного цикла программных средств … Словарь-справочник терминов нормативно-технической документации

Оценка телеметрируемого параметра — 18. Оценка телеметрируемого параметра Е. Telemetering parameter estimation Значение параметра или функциональная зависимость его от времени или другого аргумента, полученные по результатам обработки телеметрических сообщений. Примечание. Оценка… … Словарь-справочник терминов нормативно-технической документации

Оценка максимального правдоподобия — Метод максимального правдоподобия в математической статистике это метод оценивания неизвестного параметра путём максимизации функции правдоподобия. (Фишер 1912 г.[1]) Содержание 1 Определение 2 Замечание 3 Примеры … Википедия

оценка — Этим термином обозначают несколько близких, но неодинаковых, понятий, каждому из которых соответствует свой английский термин. Прежде всего, оценка (estimator) – это функция, алгоритм, словом, способ получить по выборке число (estimate), которое… … Словарь социологической статистики

ОЦЕНКА, СТАТИСТИЧЕСКАЯ — функция выборочных наблюдений для приближенной замены параметра распределения (или самого распределения). Например, для нормального распределения случайной величины средняя арифметическая – оценка математического ожидания. Точечная и интервальная … Большой экономический словарь

Источник

Статистические оценки параметров распределения

Вы будете перенаправлены на Автор24

Распределения в математической статистике характеризуется многими статистическими параметрами. Оценка неизвестных параметров распределения на основе различных данных выборки позволяет построить распределения случайной величины.

Статистические оценки можно разделить на несмещенные, смещенные, эффективные и состоятельные.

Готовые работы на аналогичную тему

Генеральная и выборочная средние

Величины генерального и выборочного среднего можно найти по следующим формулам:

С этим понятием связано такое понятие как отклонение от средней. Данная величина находится по следующей формуле:

Среднее отклонение обладает следующими свойствами:

Среднее значение отклонения равно нулю.

Генеральная, выборочная и исправленная дисперсии

Еще одними из основных параметров является понятие генеральной и выборочной дисперсии:

Генеральная дисперсия:

Выборочная дисперсия:

С этими понятия связаны также генеральная и выборочная средние квадратические отклонения:

В качестве оценки генеральной дисперсии вводится понятие исправленной дисперсии:

Также вводится понятие исправленного стандартного отклонения:

Пример решения задачи

Генеральная совокупность задана следующей таблицей распределения:

Найдем для нее генеральное среднее, генеральную дисперсию, генеральное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

Для решения этой задачи для начала сделаем расчетную таблицу:

Найдем генеральную дисперсию по формуле:

Генеральное среднее квадратическое отклонение:

Исправленное среднее квадратическое отклонение:

Источник