Что такое парабола в жизни
Что такое парабола
Содержание статьи
Математическое понятие параболы
Парабола обладает особым оптическим свойством, заключающемся в фокусировки параллельных относительно оси ее симметрии световых лучей, направленных в параболу, в вершине параболы и расфокусировки пучка света, направленного в вершину параболы, в параллельные световые лучи относительной той же оси.
Если произвести отражение параболы относительно любой касательной, то образ параболы окажется на ее директрисе. Все параболы подобны между собой, то есть для каждых двух точек A и B одной параболы, найдутся точки A1 и B1, для которых верно утверждение |A1,B1| = |A,B|*k, где k – коэффициент подобия, который в численном значении всегда больше нуля.
Проявление параболы в жизни
Некоторые космические тела, такие как кометы или астероиды, проходящие вблизи крупных космических объектов на высокой скорости имеют траекторию движения в форме параболы. Это свойство малых космических тел используется при гравитационных маневрах космических кораблей.
Для тренировок будущих космонавтов, на земле проводятся специальные полеты самолетов по траектории параболы, чем достигается эффект невесомости в гравитационном поле земли.
В быту параболы можно встретить в различных осветительных приборах. Это связано с оптическим свойством параболы. Одним из последних способов применения параболы, основанных на ее свойствах фокусировки и расфокусировки световых лучей, стали солнечные батареи, которые все больше входят в сферу энергоснабжения в южных регионах России.
Параболы в окружающем мире.
Квадратичная функция
Автор работы: Султашева Алина
Кашкарбаевна, 8 класс,
Руководитель:
Базарбаева Зайра Хайргельдыновна,
учитель математики и информатики
I. Уникальное свойство параболы.
1.1.Парабола в древности и до наших дней.
1.2.Практическое применение параболы.
1.3.Параболы в окружающем мире.
II. Изучение квадратичной функции.
2.2.Понятие квадратичной функции и ее свойства.
III. Исследование квадратичной функции.
3.1.Зависимость графика параболы от коэффициентов.
3.2.Алгоритм построения графика функции у=а(х+m)2 + n.
«Что чувство удивления – могучий источник желания знать:
от удивления к знаниям – один шаг».
Введение
В 8 классе на уроке алгебры мы впервые встретились с квадратичной функцией. Я считаю, что рассмотреть свойства этой функции и понять их с помощью графика легче.
Если рассмотреть, как абстрактные математические понятия встречаются в действительности, то предмет математики становится интересней, а наши знания более осмысленными и глубокими.
В настоящее время очень популярны нестандартные задачи, нестандартные решения и применения; я считаю, что квадратичная функция и парабола относится к разряду таких применений; поэтому выбранная мной тема актуальна.
Цель исследования: изучение некоторых свойств квадратичной функции и особенностей ее графика.
Задачи исследования:
1. Изучить роль математики в развитии цивилизации и культуры.
2. Ознакомиться с оптическими свойствами параболы, рассмотреть их применение в технике, быту.
3. Изучить некоторые свойства квадратичной функции.
4. Исследовать квадратичную функцию и составить алгоритм построения графика квадратичной функции, основываясь на её свойствах.
Объект исследования: квадратичная функция и парабола.
Предмет исследования: влияние разных коэффициентов на внешнюю форму параболы.
В своей работе я использовала следующие методы:
1) сбор и анализ литературы по теме;
4) работа с помощью программы Microsoft Office Excel.
Основными этапами исследования были:
· овладение методикой построение графиков с помощью программы Microsoft Office Excel,
· проведение опытов по построению квадратичной функции и параболы,
· обобщение полученных данных и разработка алгоритма построения графика квадратичной функции.
I. Уникальное свойство параболы.
Парабола в древности и до наших дней.
Согласно легенде, в 212 году до н.э., Архимед из Сиракуз сжёг флот римлян, обороняя свой город с помощью параболических зеркал. Этот день уцелевшим римлянам запомнился на всю жизнь. Почти полтысячи маленьких солнц вдруг загорелись на крепостной стене. Сначала они просто ослепляли, но через некоторое время произошло нечто фантастическое: передовые римские корабли, подошедшие к Сиракузам, один за другим вдруг начали вспыхивать, как факелы. Бегство римлян было паническим. Так для защиты своего города Архимед использовал оптическое свойство параболы (Приложение 1, рис.1).
Аполлоний Пергский (Перге, 262 до н.э. — 190 до н.э.) — древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н.э., он прославился в первую очередь монографией «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы. Именно Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса». Он ввёл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота, абсцисса, ордината, аппликата (Приложение 1, рис. 2, 3).
Практическое применение параболы.
В технике.
Параболоид обладает следующим свойством:
· Все лучи, исходящие из особой точки – фокуса параболы (находящегося на оси z), после отражения от «стенок» параболоида образуют лучи, параллельные оси z.
· Все лучи, параллельные оси z, после отражения от параболоида собираются в одной точке – фокусе параболоида. На этом свойстве основано конструирование автомобильных фар, прожекторов, параболических антенн и других устройств с отражающими поверхностями, имеющими формы параболоидов (Приложение 2, рис.1).
Лучи от далеких звезд приходят к нам в виде пучка параллельных лучей, двигающихся вдоль оси параболы, и отражаясь собираются в его фокусе. Если поместить туда фотопластинку, то получаем возможность усилить световой поток, идущий от звезды. На этом основана идея телескопов, антенн, локаторов, зеркала которых выполнены в виде параболоидов вращения.
В нашей стране существуют прожекторные полки, предназначенные для обеспечения боевых действий частей истребительной авиации зоны ПВО. В 1932 году в Москве формируется первый территориальный прожекторный полк. Такой полк охранял воздушные рубежи над Москвой в первые дни войны, создавая световые поля в которые то и дело врывались вражеские самолеты. На подступах к Москве самолеты противника были встречены нашими ночными истребителями и организованным огнем зенитной артиллерии. В результате этого было сбито более 200 самолетов противника. (Приложение 2, рис. 2).
Идя в ногу со временем, многие меняют телевизионную антенну. После того, как устанавливается новая параболическая, то убеждаются в том, что идет расширение диапазона, улучшение качества изображения, дальность приема передач. Эти изменения связаны с формой антенны (Приложение 2,рис.4). Параболическую антенну называют зеркальной, т.к. она состоит из основного параболического зеркала и облучателя. Электромагнитная энергия подводится к облучателю, устанавливаемому у вершины параболоида, и излучается на малое зеркало, после отражения, от которого направляется на основное зеркало. (Приложение 2, рис.5).
В космосе.
Некоторые космические тела, такие как кометы или астероиды, проходящие вблизи крупных космических объектов на высокой скорости, имеют траекторию движения в форме параболы. Скорость примерно равна 11,2 км/с и называется параболической или космической скоростью. Масса таких тел мала, а скорость велика. Поэтому они не захватываются гравитационным полем планет (звезд) и продолжают свободный полет. Это свойство малых космических тел используется при гравитационных маневрах космических кораблей.
А для тренировок будущих космонавтов, на земле проводятся специальные полеты самолетов по траектории параболы, чем достигается эффект невесомости в гравитационном поле земли (Приложение 2,рис.6,7).
В медицине.
В медицине используется параболическое устройство, за счет которого удается разрушить камень в почках. Человека помещают на кресло, и подают электричество на параболическое устройство. Все лучи концентрируются в одной точке (фокус), фокус рассчитан на особое местонахождение (заранее). В данном случае это будет сам камень в почке (Приложение 2, рис.8).
Параболы в окружающем мире.
В природе.
Когда мы прикладываем руку к уху, чтобы лучше слышать, мы неосознанно формируем параболу в трех измерениях (Приложение 3, рис.1, 2).
В архитектуре.
Параболические формы можно встретить в архитектурных сооружениях.
-Использование математического знания о геометрии конических сечений наблюдается с древнейших времен. Вполне вероятно, что строители в прошлом пользовались в этой области знания интуитивно (Приложение 3, рис.3).
-Золотые ворота — один из немногих памятников оборонного зодчества Киевской Руси периода правления Ярослава Мудрого (Приложение 3, рис.4).
-Мост Золотые Ворота — висячий мост через пролив Золотые Ворота. Он соединяет город Сан-Франциско на севере полуострова Сан-Франциско и южную часть округа Марин, рядом с пригородом Саусалито. Мост Золотые Ворота был самым большим висячим мостом в мире с момента открытия в 1937 году и до 1964 года (Приложение 3, рис.5).
— Благодаря своей отражающей способности параболы используют в постройке куполов дворцов и соборов, а также амфитеатров, чтобы зрители четко слышали актеров. (Приложение 3, рис.6).
-Архитектурные свойства арки в форме параболы делают ее идеальной математически. Перевернутая цепная линия – это арка, которая держит сама себя и не требует никаких дополнительных опор. Ворота Сент-Луиса в Миссури – прекрасный пример такой арки (Приложение 3, рис.7).
-Знаменитый испанский архитектор Гауди обожал эту кривую и использовал во многих своих творениях, например, в Каса Мила в Барселоне (Приложение 3, рис.8).
— Стадион Фишт. На нем будет открытие и закрытие Олимпиады. А так же игры Чемпионата мира по футболу 2018г. (Приложение 3, рис.11).
Применение линейной и квадратичной функций в жизни человека.
Описание презентации по отдельным слайдам:
Тема: Применение линейной и квадратичной функций в жизни человека. Авторы проекта: учащиеся 8 «Г» класса – Зиновьева Дарья, Полянских Ирина, Вещикова Наталья. Руководитель: Приймак Э.И.
Цель исследования: Поиск задач на применение линейной и квадратичной функций в жизни человека. Задачи исследования: 1) Изучение научной литературы по данной теме. 2) Решение задач по теме, оценка полученных результатов. 3) Воспитать навыки командной работы по решению проблем и интерес к предмету.
Функциональные зависимости существуют во всех сферах жизни человека.
Изучение линейной функции является актуальной всегда, т.к. с помощью неё описываются реальные процессы происходящие в природе на языке математики. С помощью линейной функции можно описать процессы движения, изменения присущие природе.
Параболу мы можем наблюдать в реальной жизни, как траекторию движения какого-либо тела. Баскетболист бросает мяч летит в корзину почти по параболе. Струя фонтана «рисует» линию, которая близка к параболе. Парабола обладает важным оптическим свойствам.
Графики зависимости физических величин, Звёздный график, Отображение звуковых волн с помощью периодической функции. С помощью гиперболических функций описывается прогиб каната, зона слышимости звука пролетающего самолета
y=kx+b, графиком является прямая. Физика. Зависимость силы тока График равномерного прямолинейного движения.
График равноускоренного прямолинейного движения ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Линза; Увеличительное стекло; Отражательный телескоп; Прожектор или фара автомобиля Звук, колебания за просторами Земли
«Пересев хуже недосева» «КАШУ МАСЛОМ НЕ ИСПОРТИШЬ»
ВЗЛЕТ РАКЕТЫ ДВЕРНОЙ ЗАМОК
Функция является неотъемлемой частью нашей жизни и наук в целом, так как функциональные зависимости, действительно, существуют во всех сферах жизни человека.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-522613
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Минпросвещения подготовило проект плана по модернизации детских лагерей в России
Время чтения: 3 минуты
В России зарегистрировали вакцину от коронавируса для подростков
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В России отцы охотнее дают деньги детям на карманные расходы, чем матери
Время чтения: 2 минуты
В России стартовал прием заявок на конкурс для журналистов-школьников «Медиабум»
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Статья «Парабола в природе»
Парабола в природе
«Когда математика стала изучать переменные
величины и функции, лишь только она научилась
описывать процессы, движение, так она стала необходима всем»
В этой статье мы поговорим о том, что такое парабола, где встречается в нашем окружении?
Парабола ( греч. Παραβολή — приложение) — геометрическое место точек на плоскости, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Параболическая орбита и движение спутника по ней:
Парабола в природе:
 |
 |
Парабола в архитектуре:
 |
Свойства параболы используются при изготовлении прожекторов, автомобильных фар,зеркал, которые имеют видпароболоидов вращения.
 |
В медицине также нашла свое применение парабола в виде контактных линз.
Также используется пароболическое устройство, за счет которого удается разрушить камень в почках.
 |
И так, как мы видим, функции и их графики окружают нас практически во всех сферах. Параболу можно встретить вокруг себя.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Эта удивительная парабола!
Авторы: Чернышёв Иван, Ямалитдинов Дамир,
8 класс, МБОУ «СОШ № 18»,
г. Миасс
Научный руководитель: Лукьянова Ольга Георгиевна,
учитель математики
2.1.Построение параболы. 10
«Что чувство удивления – могучий источник желания знать: от удивления к знаниям – один шаг»
Введение
В 7 классе на уроке алгебры мы впервые встретились с квадратичной функцией. Мы считаем, что рассмотреть свойства этой функции и понять их с помощью графика легче.
Если рассмотреть, как абстрактные математические понятия встречаются в действительности, то предмет математики становится интересней, а наши знания более осмысленными и глубокими.
В настоящее время очень популярны нестандартные задачи, нестандартные решения и применения; мы считаем, что квадратичная функция и парабола относится к разряду таких применений; поэтому выбранная нами тема актуальна.
Цель исследования: и зучение некоторых свойств квадратичной функции и особенностей ее графика.
Объект исследования: к вадратичная функция и парабола.
Предмет исследования: влияние разных коэффициентов на внешнюю форму параболы.
1. Изучить роль математики в развитии цивилизации и культуры.
2. Ознакомиться с оптическими свойствами параболы, рассмотреть их применение в технике, быту.
3. Изучить некоторые свойства квадратичной функции.
4. Исследовать квадратичную функцию и составить алгоритм построения графика квадратичной функции, основываясь на её свойствах.
В своей работе мы использовали следующие методы:
1) сбор и анализ литературы по теме;
Основными этапами исследования были:
· овладение методикой построение графиков с помощью программы Microsoft Office Excel,
· проведение опытов по построению квадратичной функции и параболы,
· обобщение полученных данных и разработка алгоритма построения графика квадратичной функции.
1.1.Парабола в древности и до наших дней
Согласно легенде, в 212 году до н.э., Архимед из Сиракуз сжёг флот римлян, обороняя свой город с помощью параболических зеркал. Этот день уцелевшим римлянам запомнился на всю жизнь. Почти полтысячи маленьких солнц вдруг загорелись на крепостной стене. Сначала они просто ослепляли, но через некоторое время произошло нечто фантастическое: передовые римские корабли, подошедшие к Сиракузам, один за другим вдруг начали вспыхивать, как факелы. Бегство римлян было паническим. Так для защиты своего города Архимед использовал оптическое свойство параболы (Приложение 1, рис.1).
Аполлоний Пергский (Перге, 262 до н.э. — 190 до н.э.) — древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н.э., он прославился в первую очередь монографией «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы. Именно Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса». Он ввёл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота, абсцисса, ордината, аппликата (Приложение 1,рис. 2, 3).
1.2.Практическое применение параболы
Параболоид обладает следующим свойством :
Лучи от далеких звезд приходят к нам в виде пучка параллельных лучей, двигающихся вдоль оси параболы, и отражаясь собираются в его фокусе. Если поместить туда фотопластинку, то получаем возможность усилить световой поток, идущий от звезды. На этом основана идея телескопов, антенн, локаторов, зеркала которых выполнены в виде параболоидов вращения.
В нашей стране существуют прожекторные полки, предназначенные для обеспечения боевых действий частей истребительной авиации зоны ПВО. В 1932 году в Москве формируется первый территориальный прожекторный полк. Такой полк охранял воздушные рубежи над Москвой в первые дни войны, создавая световые поля в которые то и дело врывались вражеские самолеты. На подступах к Москве самолеты противника были встречены нашими ночными истребителями и организованным огнем зенитной артиллерии. В результате этого было сбито более 200 самолетов противника. (Приложение 2,рис. 2).
Идя в ногу со временем, многие меняют телевизионную антенну. После того, как устанавливается новая параболическая, то убеждаются в том, что идет расширение диапазона, улучшение качества изображения, дальность приема передач. Эти изменения связаны с формой антенны (Приложение 2,рис.4). Параболическую антенну называют зеркальной, т.к. она состоит из основного параболического зеркала и облучателя. Электромагнитная энергия подводится к облучателю, устанавливаемому у вершины параболоида, и излучается на малое зеркало, после отражения, от которого направляется на основное зеркало. (Приложение 2,рис.5).
Некоторые космические тела, такие как кометы или астероиды, проходящие вблизи крупных космических объектов на высокой скорости, имеют траекторию движения в форме параболы. Скорость примерно равна 11,2 км/с и называется параболической или космической скоростью. Масса таких тел мала, а скорость велика. Поэтому они не захватываются гравитационным полем планет (звезд) и продолжают свободный полет. Это свойство малых космических тел используется при гравитационных маневрах космических кораблей.
А для тренировок будущих космонавтов, на земле проводятся специальные полеты самолетов по траектории параболы, чем достигается эффект невесомости в гравитационном поле земли (Приложение 2,рис.6,7).
В медицине используется параболическое устройство, за счет которого удается разрушить камень в почках. Человека помещают на кресло, и подают электричество на параболическое устройство. Все лучи концентрируются в одной точке (фокус), фокус рассчитан на особое местонахождение (заранее). В данном случае это будет сам камень в почке (Приложение 2, рис.8).
1.3.Параболы в окружающем мире
Когда мы прикладываем руку к уху, чтобы лучше слышать, мы неосознанно формируем параболу в трех измерениях (Приложение 3, рис.1,2).
Параболические формы можно встретить в архитектурных сооружениях.
· Использование математического знания о геометрии конических сечений наблюдается с древнейших времен. Вполне вероятно, что строители в прошлом пользовались в этой области знания интуитивно (Приложение 3,рис.3).
· Золотые ворота — один из немногих памятников оборонного зодчества Киевской Руси периода правления Ярослава Мудрого (Приложение 3,рис.4).
· Мост Золотые Ворота — висячий мост через пролив Золотые Ворота. Он соединяет город Сан-Франциско на севере полуострова Сан-Франциско и южную часть округа Марин, рядом с пригородом Саусалито. Мост Золотые Ворота был самым большим висячим мостом в мире с момента открытия в 1937 году и до 1964 года (Приложение 3,рис.5).
· Благодаря своей отражающей способности параболы используют в постройке куполов дворцов и соборов, а также амфитеатров, чтобы зрители четко слышали актеров. (Приложение 3,рис.6).
· Архитектурные свойства арки в форме параболы делают ее идеальной математически. Перевернутая цепная линия – это арка, которая держит сама себя и не требует никаких дополнительных опор. Ворота Сент-Луиса в Миссури – прекрасный пример такой арки (Приложение 3,рис.7).
· Знаменитый испанский архитектор Гауди обожал эту кривую и использовал во многих своих творениях, например, в Каса Мила в Барселоне (Приложение 3,рис.8).
· Стадион Фишт. На нем будет открытие и закрытие Олимпиады. А так же игры Чемпионата мира по футболу 2018г. (Приложение 3,рис.11).
2.1.Построение параболы.
Возьмем лист бумаги прямоугольной формы и отметим около его большой стороны точку F. Сложим лист так, чтобы точка F совместилась с какой-нибудь точкой D на большой стороне, и на бумаге образовалась линия сгиба a. Линия сгиба будет серединным перпендикуляром к отрезку FD и, следовательно, касательной к параболе. Разогнем лист и снова согнем его, совместив точку F с другой точкой большой стороны. Сделаем так несколько раз, пока вся бумага не покроется линиями сгибов. Линии сгибов будут касательными к параболе. Граница участка внутри этих сгибов будет иметь форму параболы (Приложение 4, рис. 1).
На листе бумаги нужно закрепить линейку (ее край будет директрисой будущей параболы), в точке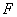 
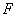
, которая станет фокусом параболы, булавкой прикрепить конец нити, другой конец которой закрепить в вершине острого угла чертежного треугольника, притом так, чтобы длина нити равнялась катету этого треугольника. Перемещая второй катет вдоль линейки и, прижимая нить острием карандаша к первому катету треугольника, мы получим кривую, точки которой находятся на одинаковых расстояниях от края линейки и от точки 
, т.е. параболу (Приложение 4, рис. 2). Оказывается, что парабола график квадратичной функции — обладает интересным свойством: есть такая точка и такая прямая, что каждая точка параболы одинаково удалена от этой точки и от этой прямой (точку называют фокусом параболы, а прямую — ее директрисой). Это свойство параболы было известно уже математикам античной Греции.
Построение параболы при заданной величине параметра p выполняется в следующей последовательности:
1. Проводят ось симметрии параболы и откладывают на ней отрезок KF=p;
2. Через точку K перпендикулярно оси симметрии проводят директрису DD1;
3. Отрезок KF делят пополам, получают вершину 0 параболы;
4. От вершины отмеряют ряд произвольных точек 1, 2, 3, 5, 6 с постепенно увеличивающемся расстоянием между ними;
5. Через эти точки проводят вспомогательные прямые перпендикулярные оси параболы;
6. На вспомогательных прямых делают засечки радиусом равным расстоянию от прямой до директрисы;
7. Полученные точки соединяют плавной кривой (Приложение 4, рис. 3).
2.2.Понятие квадратичной функции и ее свойства
Одновременно с Декартом к мысли о соответствии между линиями и уравнениями пришёл другой французский математик – Пьер Ферма (1601-1665г.г.). Он был советником Тулузского парламента и занимался математическими исследованиями лишь в свободное время. Тем не менее, Ферма получил ряд первоклассных результатов в различных областях математики. Термин функция начал применять в конце 18 века Лейбниц (1646-1716г.г.) и его ученики. Определение функции, приближённое к современному, дал Иоганн Бернулли: «Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных». (Приложение 5 рис.1)
С квадратичной функцией мы уже имели дело при работе с некоторыми формулами на уроках геометрии и физики. Например, формула S=πr² задаёт площадь круга как квадратичную функцию его радиуса r. Формула S=a² задаёт площадь квадрата как квадратичную функцию его стороны.
В уравнении квадратичной функции:
a – старший коэффициент
b – второй коэффициент
III. Исследование квадратичной функции
3.1.Зависимость графика параболы от коэффициентов
Необходимо выяснить как коэффициенты а, m , n влияют на внешнюю форму графика функции.
Оказалось, что парабола у = x 2 обладает следующими основными свойствами:
1) График функции целиком в верхней полуплоскости, принимает только неотрицательные значения. В начале координат парабола касается оси абсцисс. Это самая низкая точка графика.
Если старший коэффициент a>0, то ветви параболы направлены вверх.
Если старший коэффициент a
Вывод: график функции у =- х 2 можно получить из графика у = х 2 с помощью симметрии относительно оси Х.
Исследование 2. Сравним графики функции при различных целых значениях коэффициента ç a ç > 1. Построим графики функций у = х 2 и у = 2х 2. (Приложение 5, рис. 3).
Мы заметили что, график стал уже. Из построенного графика мы видим, что парабола растягивается относительно оси абсцисс. А такое преобразование на математическом языке называется — растяжением.
Любая точка графика y = х 2 +2 с абсциссой X находится на 2 единицы “выше”, чем точка графика y = х 2 с той же самой абсциссой; а график функции y= х 2 + 2 можно получить из графика y = f(x) параллельным переносом вдоль оси ординат на 2 единицы “вверх”.
Любая точка графика y = х 2 – 2 находится на 3 единицы “ниже”, чем точка графика y = х 2 с той же самой абсциссой; а график функции y= х 2 – 2 можно получить из графика y = х 2 параллельным переносом вдоль оси ординат на 2 единицы “вниз”.
Вывод: график функции y= f(x+ m ) можно получить из графика функции y = f(x), “сдвинув” его на | m | единиц вправо вдоль оси абсцисс, если m | m | единиц влево вдоль оси абсцисс, если m >0.
С помощью электронных таблиц мы построили графики функций, пронаблюдали за последовательностью построения графиков и составили алгоритм построения графиков функций данной модели.
3.2.Алгоритм построения графика функции у=а(х+ m ) 2 + n
0, и вправо, если m 0,и вниз, если n
Используя алгоритм, мы определили вид графика функции
1. График симметричен графику функции у=х 2 относительно оси ОХ Ветви направлены вниз.
2. Сжатие графика в 2 раза
3. График сдвинут на 4 единицы вправо.
4. График сдвинут на 7 единиц вверх. (Приложение 5, рис. 7)
Изучили значимость творческого опыта в области алгебры на примерах практического применения свойств данной кривой в различных сферах деятельности человека.
Для многих людей математика является трудной и непонятной, но мы считаем, что если подробнее изучить математические понятия и применение их в жизни, то математика становится интересной, а наши знания более осмысленными и глубокими.
На первый взгляд, понятие не ново,
И не всегда подумаешь о том,
Как важно будет в жизни это слово
И сколько смысла будет в слове том!
По-разному с годами толковали.
Сам Лобачевский руку приложил,
Чтоб слово «функция» и в средней школе знали,