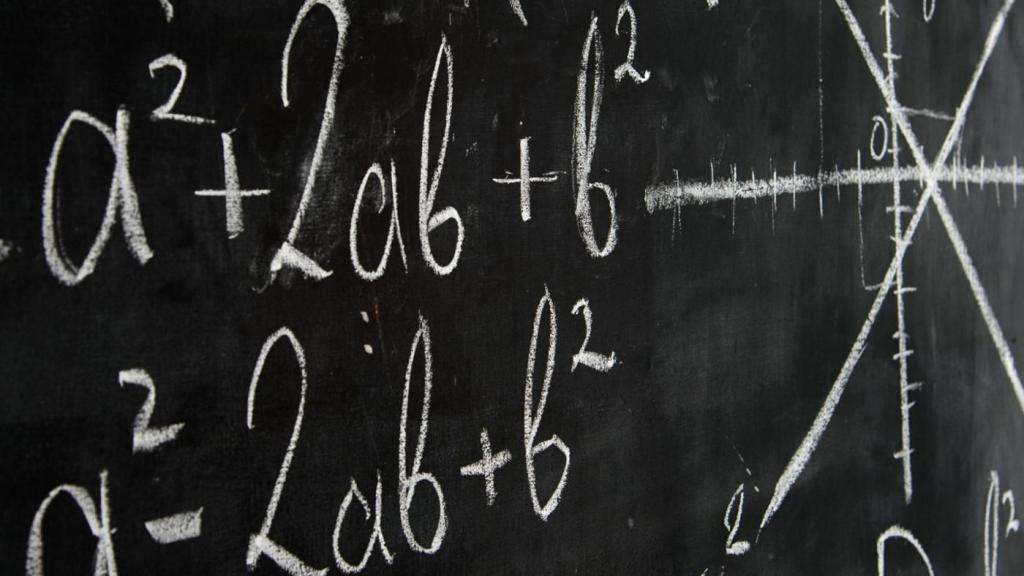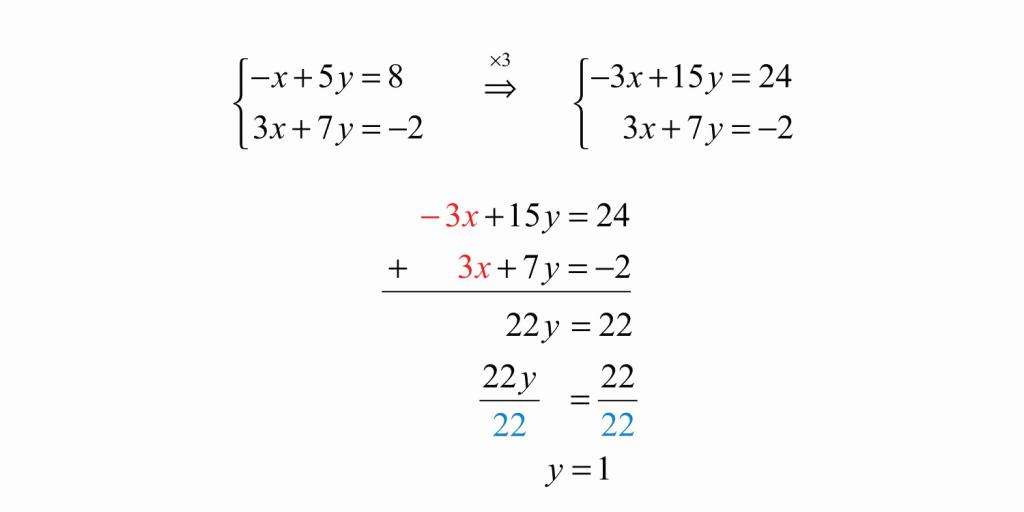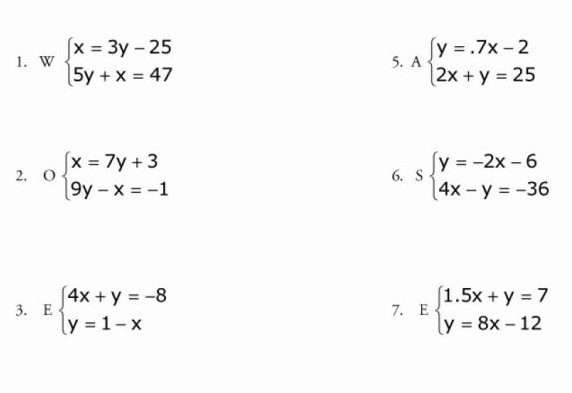Что такое переменная величина

Переменная величина

Переме́нная — атрибут физической или абстрактной системы, который может изменять своё значение. Значение может меняться в зависимости от контекста, в котором рассматривается система, или в случае уточнения, о какой конкретно системе идёт речь. Концепция переменной широко используется в таких областях как математика, естественные науки, техника и программирование. Примерами переменных могут служить температура воздуха, параметр функции и многое другое. В широком смысле, переменная характеризуется лишь множеством значений, которые она может принимать.

Содержание

Переменные в математике

В математике переменная — это величина, характеризующаяся множеством значений, которое она может принимать. [1] При этом может иметься в виду как реальная физическая величина, временно рассматриваемая в отрыве от своего физического контекста, так и некая абстрактная величина, не имеющая никаких аналогов в реальном мире. В математическом анализе и большинстве смежных разделов математики под «переменной» обычно понимают численную величину, множество принимаемых значений которой включено в множество вещественных чисел.

Множество всех значений, которые может принимать данная переменная, называется областью изменения этой переменной. Это множество и задаёт переменную, то есть формально и является ей.

При моделировании переменные необходимо отличать от параметров, несмотря на то что переменная в одном контексте может быть параметром в другом.

В прикладной статистике переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами.

Обозначения

Нужно отметить, что аналогичным образом обозначаются неизвестные в уравнениях, неравенствах и других подобных задачах. Например, . В этом случае имеются ввиду не переменные, хотя понятия весьма схожи и зависят от контекста.

Суть этого различия между неизвестной и переменной можно пояснить так. Запись можно, с одной стороны, трактовать как утверждение о свойстве неизвестной (в момент высказывания утверждения) величины , значение которой можно найти (или уточнить), отталкиваясь от приведенного утверждения как от исходной посылки. В этом случае будет обозначением конкретной, но до проведения выкладок (например, решения уравнения) неизвестной величины. С другой стороны запись можно трактовать как предикат, принимающий значение «истина» при одних значениях, подставляемых на место , и значение «ложь» при других. В этом случае является обозначением места в выражении, на которое могут подставляться различные (переменные) значения с целью определения логического (булева) значения записанного предиката. В этом случае правильнее рассматривать как переменную.

Переменные в программировании

В программировании переменная — это идентификатор, определяющий данные. Обычно это бывает имя, скрывающее за собой область памяти с хранящимися там данными. Переменная может иметь тип, характеризующий множество значений, которые она может принимать. В программировании, переменные, как правило, обозначаются одним или несколькими словами или символами, такими, как «time», «x», «foo» и тому подобное.

Следует отметить, что это значение в некотором смысле схоже с математическим. Математики в XVII веке придумали переменную именно для того, чтобы «забронировать» в формуле место, на которое в нужный момент можно подставить конкретное значение. Бумага в этом процессе является памятью, а обозначения (чаще, буквы) резервируют и именуют области этой памяти. Ощущение неоднозначности возникает из-за того, что формула в математике играет двоякую роль: если это алгоритм вычисления, смысл совпадает с программистским определением; если же формула визуализирует отношения своих элементов, мы абстрагируемся от роли переменной, как ячейки памяти, такое понимание теряет смысл.

Переменные в физике

В физике переменная — это некоторый атрибут модели реального физического процесса, принимающий количественные значения, физическая величина. Множество значений, которые может принимать конкретная переменная, определяется из физических соображений. Физические переменные связываются друг с другом физическими законами, в результате чего получаются математические модели различной степени сложности. Переменные в физике, как правило, кроме количественного значения характеризуются также размерностью.

Источник

Что такое переменные? Переменная величина в математике

Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.

Понятие переменной

Вам будет интересно: Плотность осмия: характеристика, значение, физические и химические свойства, получение и применение

Вам будет интересно: Российская таможенная академия в Москве: описание, адрес, факультеты.

Виды величин

Вам будет интересно: Конспект урока русского языка во 2 классе. Правила «жи – ши», «ча – ща», «чу – щу»

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).

Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.

С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:

За x2 принимаем некое k, и уравнение приобретает понятный вид:

Вот какую пользу в математику несет введение переменных.

Неравенства, примеры решения

Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Вам будет интересно: Французские местоимения: типы и виды

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

Пример с одной переменной:

Делим обе части неравенства на 10 и получаем:

Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.

Квадратные неравенства

Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

По формуле корней квадратного уравнения получаем:

Или можно было решить это уравнение по теореме Виета:

Методом подбора получаем такие же корни уравнения.

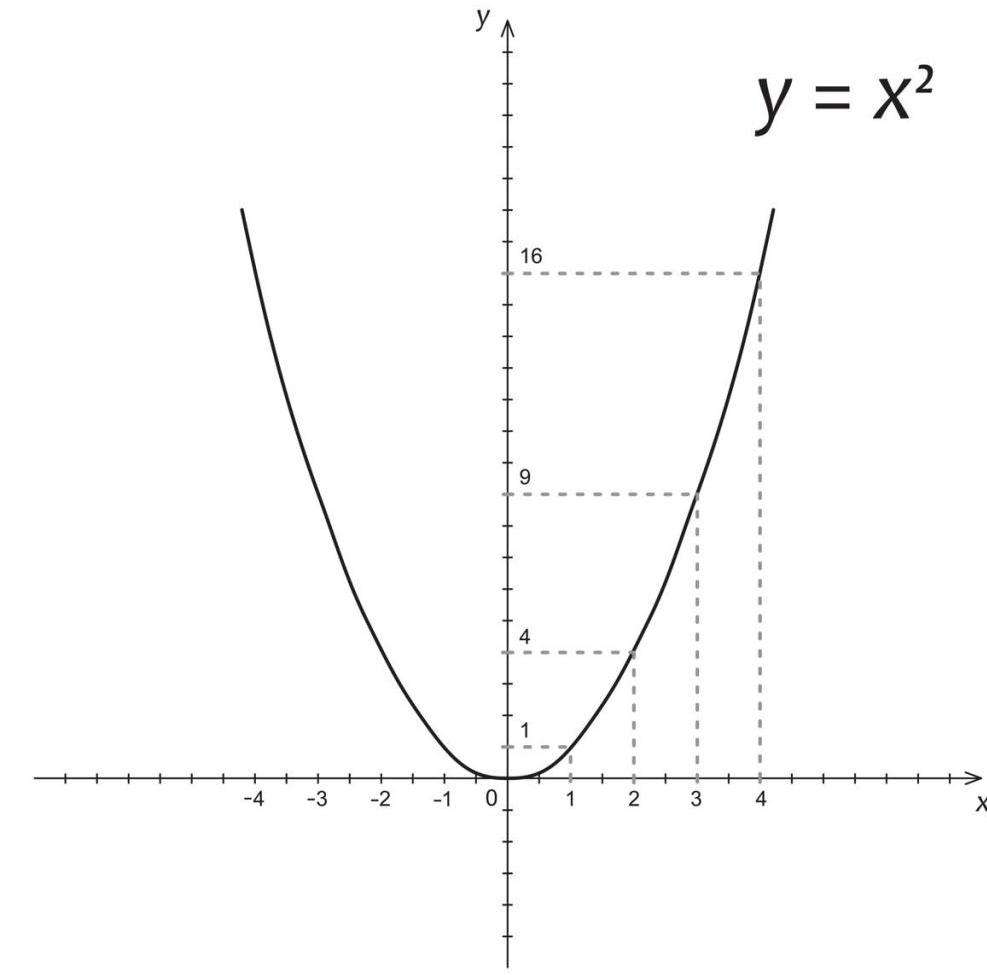
Парабола

1. Определяем, куда направлены ветви параболы.

2. Приравниваем функцию к нулю и находим корни уравнения.

3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.

Выписываем в виде функции:

Приравниваем к нулю.

Дальше решаем как квадратное уравнение и находим нули функции:

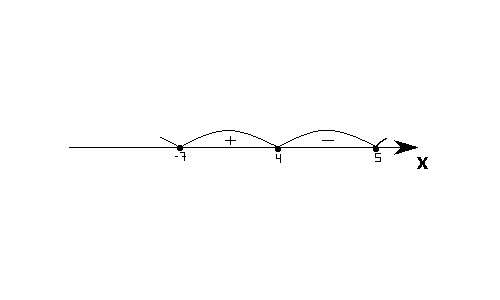
Метод интервалов

1. Находим корни уравнения, при которых неравенство равно нулю.

2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.

3. Определяем знак любого интервала.

4. Расставляем знаки у остальных интервалов, меняя их через один.

2) Изображаем их на числовой прямой.

3) Определяем знаки интервалов.

2. Отмечаем их на числовой прямой.

3. Определяем знаки интервалов.

Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.

Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.

Системы уравнений

Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.

Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.

Алгебраический метод

Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.

Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:

Решаем получившееся уравнение и находим икс.

Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:

Метод подстановки

Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.

В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:

Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:

Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:

Источник

Переменная

Переменное, одно из основных понятий математики и логики. Начиная с работ П. Ферма, Р. Декарта, И. Ньютона, Г. В. Лейбница и др. основоположников «высшей» математики под П. понимали некоторую «величину», которая может «изменяться», принимая в процессе этого изменения различные «значения». Тем самым П. противопоставлялись «постоянным» (или константам) — числам или каким-либо др. «величинам», каждая из которых имеет единственное, вполне определённое значение (см. Переменные и постоянные величины). По мере развития математики и в ходе её обоснования представления о «процессах», «изменении величин» и т. п. тщательно изгонялись из математического арсенала как «внематематические», в результате чего П. стала пониматься как обозначение для произвольного элемента рассматриваемой предметной области (например, области натуральных чисел или действительных чисел), то есть как родовое имя всей этой области (в отличие от констант — «собственных имён» для чисел или др. конкретных предметов рассматриваемой области). Этот пересмотр взглядов на понятие П. был тесно связан с перестройкой математики на базе множеств теории (См. Множеств теория), завершившейся в конце 19 в. При всей простоте и «естественности» такой перестройки она существенным образом опирается на так называемую абстракцию актуальной бесконечности, позволяющую рассматривать произвольные бесконечные множества в качестве «данных» («завершенных», «готовых», «актуальных») объектов и применять по отношению к ним любые средства классической логики, отвлекаясь от незавершённости и принципиальной незавершимости процесса образования такого множества. Трудности решения логических проблем, связанных с принятием этой абстракции, делают понятной частичную «реабилитацию» старинных представлений о «переменных величинах»; при построении математических теорий представители некоторых школ (см. Математический интуиционизм, Конструктивное направление) предпочитают обходиться боле (слабой, но зато менее уязвимой в логическом отношении абстракцией потенциальной осуществимости, с точки зрения которой с бесконечными множествами как раз связываются представления о процессах их «порождения»,— сколь угодно далеко заходящих, но никогда не завершающихся (см. Бесконечность в математике). При исследовании вопроса непротиворечивости (См. Непротиворечивость) различных областей математики на такую позицию фактически встаёт значительное большинство математиков и логиков (см. Метаматематика).

В формализованных языках (исчислениях (См. Исчисление), формальных системах) математической логики П. называются символы строго фиксированного вида, могущие при определённых условиях заменяться выражениям данного исчисления. Это относится к так называемым свободным (или значащим) П. примером которых может служить П. в неравенстве х > 5, обращающемся при подстановке вместо х, скажем, цифры 7 (то есть обозначения для числа) 7 в истинное высказывание, а при подстановке цифры 2 — в ложное высказывание. Что касается так называемых связанных (или фиктивных) П., то они сами по себе вообще ничего не означают, несут чисто синтаксические функции и могут (при соблюдении некоторых элементарных предосторожностей) «переименовываться», то есть заменяться др. П. Такова, например, П. 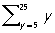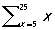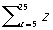у в записях или ∀yP (y), в интерпретации (прочтения) которых она вообще не входит и может быть заменена любой др. П. так, первая из них (читаемая как «сумма целых чисел от 5 до 25») может быть заменена на или , а вторая («все числа обладают свойством Р») на ∀tP (t). Различают индивидные, пропозициональные, предикатные, функциональные, числовые и др. виды П., вместо которых можно (согласно специальным правилам подстановки) подставлять соответственно обозначения предметов из рассматриваемой области («термы»), обозначения для конкретных высказываний, предикатов, функций, чисел и др. Т. о., П. можно содержательно понимать как «пустое место» в формуле, снабженное указанием, чем это «место» может быть «заполнено» (своего рода «тара под строго определенный товар»).

Свободные вхождения П. в выражения содержательных научных теорий и формулы логико-математических исчислений (соответствующие употреблению неопределенных местоимений в обычной речи) допускают различные интерпретации. Первая (соответствующая применению всякого рода процедур подстановок) — так называемая предикатная интерпретация: формула A (x₁. x_n) какого-либо исчисления понимается как некоторый местный Предикат. Та же формула может интерпретироваться и как предложение (Высказывание), а именно как предложение ∀x₁ … ∀x_n A (x₁ … x_n), являющееся ее «замыканием»,— это так называемая интерпретация всеобщности (употребительная, например, при формулировке аксиом (См. Аксиома) различных научных теорий). Свободным П. могут, наконец, приписываться значения, постоянные в пределах некоторого контекста (например, вывода из данной совокупности формул), их тогда называют параметрами этого контекста и говорят об их условной интерпретации. Например, П. х в выражении cos х, взятом изолированно, имеет предикатную интерпретацию, в тождестве sin 2 x + cos 2 x = 1 — интерпретацию всеобщности, в уравнении cos х = 1 (в процессе его решения, когда эта П. именуется «неизвестным») — условную интерпретацию.

Таким образом, на различных уровнях формализации понятие П. выступает как уточнение средств, общеупотребительных в обычных разговорных языках (неопределенные местоимения, неопределенные артикли), и различных способов использования этих средств.

Лит.: Клини С. К, Введение в метаматематику, пер с англ, М., 1957, §§ 31, 32, 45, Чёрч А, Введение в математическую логику, пер с англ, т. 1, М., 1960, §§ 02, 04, 06.

Источник

Что такое переменная величина в математике

Содержание статьи

Переменные

Основным показателем переменной является то, что она записывается не числом, а буквой. Под условным обозначением чаще всего скрывается определенное значение. Переменная получила свое название благодаря тому, что ее значение меняется в зависимости от уравнения. Как правило, любая буква алфавита может быть использована в качестве обозначения для такого элемента. Например, если вы знаете, что у вас есть 5 рублей и вы хотите купить яблоки, которые стоят 35 копеек, конечное количество яблок, которые можно купить, обозначается буквой (например «С»).

Пример использования

Если есть переменная, которая была выбрана по вашему усмотрению, необходимо составить алгебраическое уравнение. Оно будет связывать между собой известные и неизвестные величины, а также показывать связь между ними. Это выражение будет включать в себя цифры, переменные и одну алгебраическую операцию. Важно отметить, что выражение будет содержать знак равенства.

Полное уравнение содержит значение выражения в целом. Оно отделено от остального уравнения знаком равенства. В предыдущем примере с яблоками 0.35 или 35 копеек, умноженные на «С», является выражением. Для того чтобы создать полное уравнение, необходимо записать следующее:

Мономиальные выражения

Полиномы

Зависимые и независимые переменные

В математике независимыми переменными являются неизвестные, которые определяют другие части уравнения. Они стоят отдельно в выражениях и не изменяются вместе с другими переменными.

Значения зависимых переменных определяются с помощью независимых. Их значения зачастую определяются эмпирически.

Источник

Переменная величина

Переменная характеризуется только множеством значений, которые она может принимать. Переменную обозначают символом, общим для каждого из её значений.

Русский термин «переменная величина» происходит от латинской формулировки quantitas variabilis, также как в русском языке сокращаемой до единственного слова variabilis.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями.

В математике (особенно в теории категорий), коммутативная диаграмма — изображаемая в наглядном виде структура наподобие графа, вершинами которой служат объекты определённой категории, а рёбрами — морфизмы. Коммутативность означает, что для любых выбранных начального и конечного объекта для соединяющих их ориентированных путей композиция соответствующих пути морфизмов не будет зависеть от выбора пути.

Измери́мые функции представляют естественный класс функций, связывающих пространства с выделенными алгебрами множеств, в частности измеримыми пространствами.

Конечная разность — математический термин, широко применяющийся в методах вычисления при интерполировании.

Прострáнством называется математическое множество, имеющее структуру, определяемую аксиоматикой свойств его элементов (например, точек в геометрии, векторов в линейной алгебре, событий в теории вероятностей и так далее).Подмножество пространства называется «подпространством», если структура пространства индуцирует на этом подмножестве структуру такого же типа (точное определение зависит от типа пространства).

В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.

Источник