Что такое площадь квадрата 3 класс правило математика

Площадь фигур

Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см 2

Формулу площади квадрата, зная определение степени, можно записать следующим образом:

Площадь прямоугольника

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см 2

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м 2
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м 2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м 2

Ответ: S = 65 м 2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см 2

S _ABC = S_ABCD : 2

S _ABC = 20 : 2 = 10 см 2

S _ABC = S _ACD = 10 см 2

Источник

Площадь фигуры

В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.

Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией

Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.

Сравнение площадей фигур

При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.

Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.

Сравнение площадей способом наложения

Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.

Сравнение площадей заданной меркой

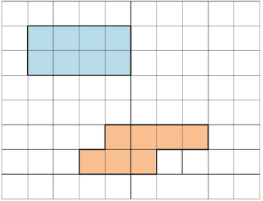
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.

Например, меркой может быть вот такой прямоугольник :

В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.

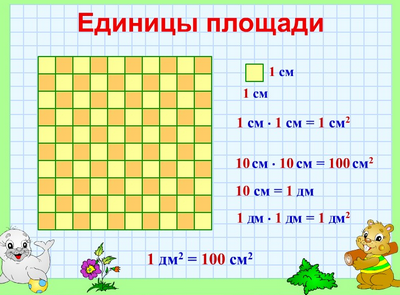
Единицы площади

В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.

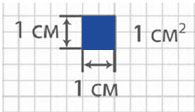
Квадратный сантиметр

Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²

Определим площадь данных фигур:

В синей фигуре 8 см², а в красной фигуре – 7 см².

8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.

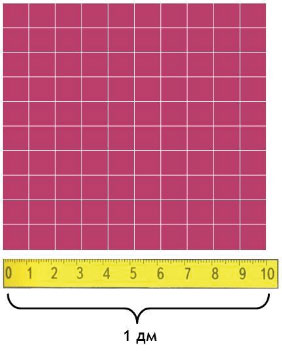
Квадратный дециметр

Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²

Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:

Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть

Значит, 1 дм² = 100 см²

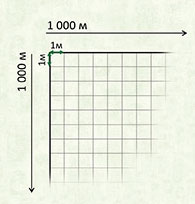
Квадратный метр

Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²

Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.

1 м² = 100 дм²

Квадратный километр

Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²

Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.

1 км² = 1000000 м²

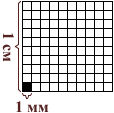
Квадратный миллиметр

Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²

Этой единицей мы пользуемся для измерения очень маленьких площадей.

1 см² = 100 мм²

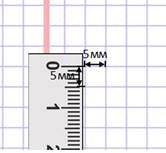
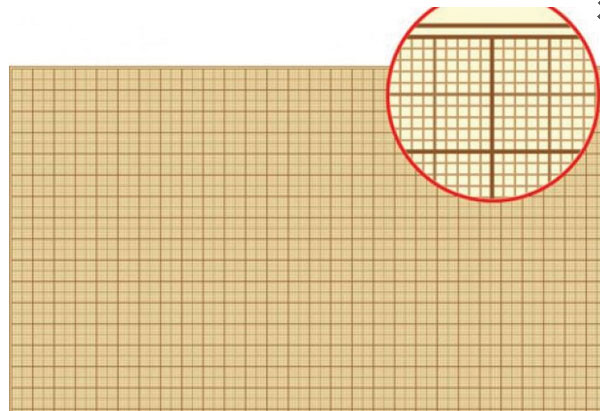
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.

Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Ар

Слово «ар» при числах сокращённо записывают так:

Гектар

Слово «гектар» при числах сокращённо записывают так:

Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.

Ар и гектар используются при измерении земельных участков.

Поделись с друзьями в социальных сетях:

Источник

Как определить площадь квадрата

Формула нахождения площади квадрата

Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где d — диагональ.

Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Популярные единицы измерения площади:

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Воспользуемся формулой: S = d 2 : 2.

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d

Диаметр окружности равен двум радиусам:
d = 2r

Получается, что сторона равна двум радиусам:
a = 2r

Используем формулу нахождения площади квадрата через сторону:
S = a 2

Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2

Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2

Источник

Урок математики на тему: «Площадь квадрата» (3 класс)

Муниципальное казенное общеобразовательное учреждение

«Солигаличская средняя общеобразовательная школа»

Солигаличского муниципального района Костромской области

Урок математики в 3 классе

Тема: «Площадь квадрата»

УМК «Планета знаний»

учебник М.И. Башмаков, М.Г. Нефёдова

«Математика 3 класс, 2 часть»

Малегина Ирина Валентиновна,

учитель начальных классов

г. Солигалич 2019 г.

Тема урока: «Площадь квадрата».

Тип урока: урок открытия нового знания.

Цель урока: обеспечить усвоение детьми способа нахождения площади квадрата.

Способствовать формированию ключевых компетентностей: познавательной, информационной, коммуникативной, развивающей.

Вывести правило вычисления площади квадрата.

Актуализировать знания о признаках и свойствах геометрических фигур.

Способствовать совершенствованию вычислительных навыков.

Способствовать развитию основных операций мышления (сравнение, обобщение, умение делать выводы на основе полученной информации).

Развитие умения анализировать и находить пути решения поднимаемой проблемы.

Формирование основных компонентов УУД (умение ставить учебную задачу, обобщать, делать выводы)

Формировать навыки самоанализа.

Создавать условия для снятия физической и умственной усталости детей.

Используемые методы обучения

1.Методы управления учебной деятельностью и восприятия информации:

а) по источнику передачи и восприятия информации – словесные, наглядные, практические;

б) по логике передачи и восприятия информации – индуктивные и дедуктивные;

в) по степени самостоятельности учащихся – репродуктивные и проблемно-поисковые;

г) по степени управления учебной деятельностью – учебная деятельность, организованная и управляемая учителем, самостоятельная деятельность уч-ся, работа с учебником.

3. Методы контроля и самооценки

а) фронтальная работа, опрос;

— Способность к самооценке на основе критерия успешности учебной деятельности.

— Уметь определять и формулировать цель на уроке с помощью учителя;

проговаривать последовательность действий на уроке;

уметь высказывать своё предположение на основе работы с материалом учебника;

уметь работать по коллективно составленному плану;

оценивать правильность выполнения действия на уровне адекватной оценки;

вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; планировать своё действие в соответствии с поставленной задачей.

— Уметь оформлять свои мысли в устной форме;

слушать и понимать речь других;

учиться работать в группе, формулировать собственное мнение и позицию.

— Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;

добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

— Уметь использовать в речи термины «длина», «ширина», «площадь».

— Уметь вычислять площадь прямоугольника, квадрата.

— Знать основные понятия длина, ширина, площадь

Оборудование: компьютер, мультимедийный проектор, презентация к уроку, учебник, тетрадь, линейка.

-Поприветствуем друг друга, подарим улыбку и хорошее настроение!

Думать – коллективно!
Решать – оперативно!
Отвечать – доказательно!
Работать – старательно!
И открытия нас ждут обязательно!

-Продолжаем путешествие по городу математических наук, где встречи с вами ждут известные нам герои Фея, Волшебный Почтальон, Юлика и Алеша.

Поспешим на главную площадь к волшебному фонтану.

(На волшебных каплях фонтана записаны выражения. Ученики решают, на обратной

стороне капли читают пожелание на урок:

Будьте внимательны!, Новых открытий!, Любознательности!, Умейте договариваться!

— Чему равно произведение чисел 8 и 8? 64

— Найдите произведение чисел 3 и 3. 9

— Чему равно частное чисел 25 и 5? 5.

— Уменьшите 81 в 9 раз. 9

— Увеличьте 4 в 4 раза. 16

— Найдите произведение чисел 6 и 6. 36

— Делимое 49, делитель 7, найдите частное. 7

3. Актуализация знаний и фиксация затруднений в деятельности.

-Веселый Почтальон принес вам конверты. Откройте их.

-Что в конвертах? (геометрические фигуры)

-Разделите фигуры на две группы.

-Какие группы? (Прямоугольники, квадраты)

-Как найти площадь прямоугольника?

(Длину умножить на ширину)

-Какие единицы измерения площади вы знаете?

-Как измерить площадь данного прямоугольника в см²?

-Найдите, пожалуйста, площадь синего прямоугольника.

С чего начнем? (Надо измерить стороны и вычислить площадь)

Длина – 5 см, ширина – 3 см. Площадь – 15 кв.см.

-Найдите, пожалуйста, площадь зеленого прямоугольника.

-Чем похожи прямоугольники и квадраты?

(Прямые углы, четыре стороны, это прямоугольники)

-Зная, как найти площадь прямоугольника, попробуйте, найти площадь квадрата, со

-Хотите узнать? Тогда поставьте цель нашего урока?

(Узнать, как записать площадь квадрата другим способом)

5. Сообщение темы урока.

-Какая будет тема урока?

(открываю тему на доске: Площадь квадрата)

6. Построение проекта выхода из затруднения.

-Мы с вами поставили цель – узнать, как записать площадь квадрата другим способом. Что вам поможет справиться с этим?

-Обратимся за помощью к самой умной Фее города математических наук. Она приготовила вам алгоритм вычисления площади.

-Посмотрим ещё раз на прямоугольник.

-Правило нахождения площади можно записать в виде формулы.

-Давайте подумаем как?

-Площадь в математике принято обозначать буквой – S

Длина прямоугольника – a

Как узнать площадь?

-Вот вы сами и вывели формулу нахождения прямоугольника, с помощью которой мы будем находить площадь любого прямоугольника.

-Так как у квадрата все стороны равны, значит и значение сторон тоже равно.

-И мы можем записать площадь квадрата таким способом: а х а= а в квадрате.

Другими словами: если множитель повторяется два раза, то в математике принято

-Ребята – это правило можно сформулировать иначе. Для этого откройте учебник на с.38 и прочитайте правило в рамочке.

-Давайте запишем новый способ нахождения площади квадрата в тетради.

-Давайте найдём площадь квадрата со стороной 4 см новым способом

4 х 4 = 4 в квадрате = 16 кв.см

-А теперь давайте запишем произведение двух одинаковых множителей

-А теперь выполним следующее задание.

Площадь квадрата равна 64 квадратных сантиметров. Чему равна сторона квадрата?

7. Первичное закрепление

Герои нашего волшебного города Юлика и Алеша просят вашей помощи. Им необходимо рассчитать площади газонов и клумб на главной площади. Поможем?

-Поработаем в парах. У вас на столе лежат карточки, возьмите их, пожалуйста, и решите задания вместе.

6 х 6 = 6 в квадрате = 36 кв.см

-Получилось? Давайте проверим по эталону.

-Проговорите друг другу новый способ нахождения площади квадрата.

8. Самостоятельная работа с самопроверкой

-Прочитайте задание в учебнике на с.38 под №1.

-Чему равна сторона клетки?

-Чему будет равна площадь клетки?

-Запишите площадь квадратов новым способом самостоятельно.

-Проверяем. Давайте запишем площади квадратов.

-Оцените себя, как вы справились с этим заданием.

— Прочитайте задание на с.39 учебника №4

-Давайте выполним (запись на доске)

11х11=11 в квадрате =

-А чтобы было быстро записать результат, воспользуемся таблицей квадрата числа на

11х11=11 в квадрате=121

-Вам понятно?.Тогда выполним это задание у доски.

(один у доски, остальные в тетрадях)

Вот и подошло к своему завершению путешествие по волшебному городу

-Какую цель мы ставили на данном уроке?

-Нам удалось достичь цели?

-Вы смогли справиться с трудности?

– Что понравилось на уроке?

10. Домашнее задание

— Учебник с. 38, правило, стр.39 № 7.

Покажите своё настроение (рисуют на полях тетради смайлик веселый или грустный).

-На этом наш урок закончился, благодарю всех.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Скоростное чтение

Курс повышения квалификации

Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО

Ищем педагогов в команду «Инфоурок»

Конспект урока математики в 3 классе. УМК «Планета Знаний» учебник «Математика 3 класс, 2 часть», авторы М.И. Башмаков, М.Г. Нефёдова

Тема урока: «Площадь квадрата».

Тип урока: урок открытия нового знания.

Цель урока: обеспечить усвоение детьми способа нахождения площади квадрата.

Способствовать формированию ключевых компетентностей: познавательной, информационной, коммуникативной, развивающей.

Номер материала: ДБ-438669

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Школьники из России выиграли 8 медалей на Международном турнире по информатике

Время чтения: 3 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

ОНФ проверит качество охраны в российских школах

Время чтения: 2 минуты

Создана Ассоциация руководителей школ России и Беларуси

Время чтения: 1 минута

Детский омбудсмен предложила обучать педагогов мотивированию учащихся

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Понятие площади многоугольника

Понятие площади уже знакомо нам из младших классов и повседневной жизни. Эта величина, которая, грубо говоря, характеризует размер плоских фигур. Она показывает, какую часть плоскости занимает та или иная фигура. Исторически понятие площади многоугольника считалось неопределяемым, так же как понятия точка, прямая, плоскость и т. д. Основная же задача геометров (а именно так называют математиков, специализирующихся на геометрии) сводилась к измерению площади.

Как известно, для проведения любых измерений должна существовать некоторая единица измерения. Так, массу измеряют в килограммах, длину – в метрах и т. д. При этом единицы измерения разных величин могут быть связаны друг с другом. С практической точки зрения удобно принять в качестве единицы измерения площади квадрат, сторона которого равна 1 метру. Принимается, что площадь такого квадрата равна 1 квадратному метру (обозначается символом м 2 ):

Аналогично можно определить такие величины, как квадратный сантиметр (см 2 ), квадратный километр (км 2 ), квадратный миллиметр (мм 2 ) и т.д.:

Как мы знаем, иногда в задачах единицу измерения длины не указывают вовсе. Например, говорят, что сторона квадрата равна единице. В таких случаях и площадь является безразмерной величиной. Принимается, что площадь квадрата со стороной, равной единице, также равна единице. Такой квадрат называется единичным.

Общепринято, что площадь фигуры обозначается буквой S.

Свойство аддитивности площади

Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:

Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.

В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.

Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.

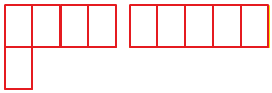
Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:

Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:

Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут. Равносоставленные же фигуры могут и не накладываться друг на друга.

Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны. Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.

Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.

Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:

Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m 2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R 2 ):

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Соотношение между единицами измерения площадей

Существуют специальные единицы измерения площади, известные как ар (обозначается сокращением а) и гектар (сокращение га). Первый представляет собой квадрат со стороной 10 м, а второй – со стороной 100 м. Верны следующие соотношения:

В частности, если стороны квадратов отличаются в 10 раз, то их площади отличаются уже в 100 раз. Отсюда вытекает быстрый метод перевода единиц площади. Пусть надо перевести 1 квадратный километр в квадратные дециметры. Сначала мы считаем, во сколько раз километр длиннее дециметра:

Решение. Миллиметр в 10 раз меньше сантиметра, а потому 1 см 2 равен 100 мм 2 :

Площадь прямоугольника

Ещё из младшей школы известно, что площадь прямоугольника равна произведению его сторон. Докажем этот факт, используя только свойства площади и выведенную нами ранее формулу площади квадрата.

Возьмем произвольный прямоугольник со сторонами a и b. Далее достроим его до квадрата со стороной (а + b):

Итак, мы доказали следующее утверждение:

Задание. Найдите площадь прямоугольника со сторонами 5 и 8 см?

Решение. Просто перемножаем эти числа:

Задание. Найдите площадь фигуры, изображенной на рисунке:

Решение. Необходимо разбить фигуры на несколько прямоугольников:

Далее считаем площадь каждого отдельного прямоугольника:

Задание. Полкомнаты необходимо покрыть паркетом. Длина и ширина комнаты равны 6 и 5,5 метрам, а каждая дощечка паркета имеет габариты 30х5 см. Сколько дощечек паркета необходимо купить для ремонта?

Решение. В таких задачах прежде всего следует все длины выразить в одних единицах измерения. Перепишем габариты комнаты:

Важно убедиться, что пол можно полностью покрыть целым числом дощечек, не используя какие-либо дощечки наполовину. Для этого габариты дощечки должны быть кратны габаритам комнаты. Это условие соблюдается:

Получается, что для покрытия пола дощечки необходимо разместить их в 20 рядов, в каждом из которых будет 110 досок. Тогда общее количество досок будет равно

Задание. Площадь прямоугольника равна 64, а одна из его сторон имеет длину 16. Найдите вторую сторону прямоугольника.

Решение. Запишем формулу площади прямоугольника:

Задание. Найдите стороны прямоугольника, если площадь равна 500, а одна из сторон в 5 раз больше другой стороны.

Решение. Обозначим меньшую сторону переменной х. Тогда большая сторона будет в 5 раз больше, то есть она равна 5х. Площадь прямоугольника будет вычисляться как произведение этих чисел

Мы получили два значения х, 10 и (– 10). Естественно, длина отрезка не может выражаться отрицательным числом, поэтому нам подходит только значение 10. Это длина меньшей стороны. Большая же сторона в 5 раз длиннее, то есть ее длина равна

Решение. Снова обозначим длину меньшей стороны буквой х, тогда большая сторона будет иметь длину х + 5 см. По условию произведение этих сторон равно 150:

Это обычное квадратное уравнение, решаемое с помощью:

Снова получили два корня, из которых только один является положительным. Итак, меньшая сторона равна 10 см. Тогда большая сторона буде равна

Решение. Обозначим смежные стороны буквами a и b. Тогда и две другие стороны также будут равны а и b. Так как периметр (его обозначают буквой Р) по определению является суммой длин всех сторон, то для прямоугольника он будет равен:

Если сюда вместо S подставить 15, а вместо а выражение 8 – b, то получим такое уравнение:

Оба полученных корня являются положительными числами, то есть устраивают нас. Зная b, легко найдем и a:

В первом случае получается, что стороны равны 3 и 5 см. Во втором случае получились те же числа, только в другом порядке: 5 и 3 см. То есть эти два ответа, по сути, идентичны друг другу.

Источник