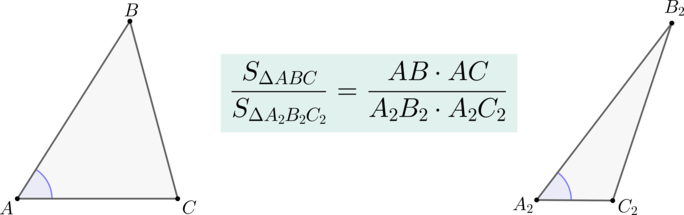Что такое площадь многоугольника
Понятие площади многоугольника
За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков.
| единица измерения отрезков | единица измерения площадей | название квадрата |
| мм | мм 2 | квадратный миллиметр |
| см | см 2 | квадратный сантиметр |
| дм | дм 2 | квадратный дециметр |
| м | м 2 | квадратный метр |
| км | км 2 | квадратный километр |
При выбранной единице измерения площадей площадь каждого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в данном многоугольнике.
Свойства площадей
Свойства 1 0 и 2 0 называют основными свойствами площадей.
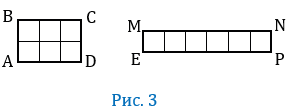
Равносоставленные многоугольники — это многоугольники, которые составлены из многоугольников, имеющих равные площади. На рисунке 3 изображены два равносоставленных многоугольника.
Любые два равносоставленных многоугольника равновеликие.
Поделись с друзьями в социальных сетях:
Понятие площади многоугольника
Урок 9. Геометрия 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Понятие площади многоугольника»
В повседневной жизни нам часто встречается понятие площади. Мы говорим о площади земельного участка, площади озера, площади комнаты.
На этом уроке мы будем вести речь о площади многоугольников.
Площадь многоугольника – это величина части плоскости, которую занимает многоугольник.
Прежде, чем говорить об измерении площади многоугольника, давайте вспомним, как мы измеряем длину отрезка.
Измерение отрезков основано на сравнении их с некоторым отрезком, принятым за единицу измерения.
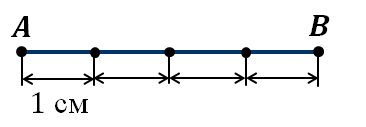
Так, например, определим длину некоторого отрезка AB, приняв за единицу измерения сантиметр.
Видим, что сантиметр в данном отрезке укладывается ровно четыре раза, а значит, его длина равна четырём сантиметрам.
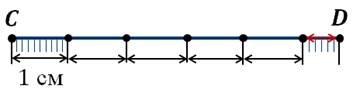
А вот в отрезке CD сантиметр укладывается пять раз, но при этом получается остаток.
В таком случае надо разделить единицу измерения на равные части, обычно делят на десять частей, и определить, сколько таких частей укладывается в остатке. В нашем случае в остатке шесть раз укладывается десятая часть отрезка, поэтому длина отрезка CD= 5,6 см.
Аналогично проводится и измерение площадей.
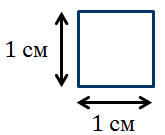
За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Например, если за единицу измерения отрезков принят сантиметр, то за единицу измерения площадей принимают квадрат со стороной один сантиметр.
Таким же образом определяется:
Квадратный миллиметр (мм 2 )
Квадратный метр (м 2 )
Квадратный километр (км 2 )
Отметим, что площадь обозначается буквой S.
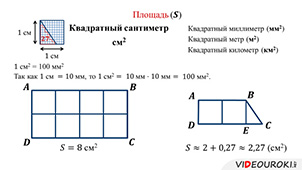
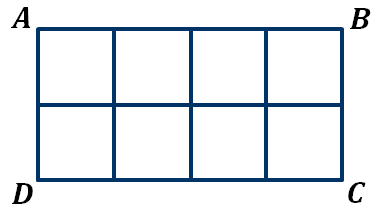
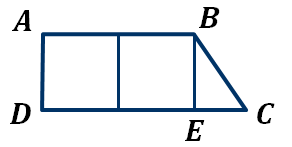
Давайте измерим площадь прямоугольника ABCD.
В прямоугольной трапеции ABCD квадратный сантиметр укладывается два раза, но при этом остается часть трапеции – треугольник BDE, в котором квадратный сантиметр не укладывается целиком.
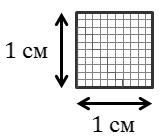
Чтобы измерить площадь этого треугольника, мы разобьём квадрат со стороной один сантиметр на более мелкие квадратики со стороной один миллиметр.
При этом у нас получится сто маленьких квадратиков.
То есть в одном сантиметре квадратном умещается сто миллиметров квадратных.
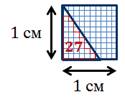
Теперь поместим наш треугольник BDE в этот квадрат.
Видим, что квадратный миллиметр укладывается целиком двадцать семь раз, но остается ещё часть, в которой квадратный миллиметр не укладывается целиком.
Мы могли бы продолжить деление квадратного миллиметра на ещё более мелкие квадратики, чтобы получить более точный результат, но давайте пока остановимся и запишем результат приблизительно.
Итак, 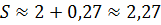
Рассмотренный процесс измерения площадей не совсем удобен. И на практике для вычисления площадей геометрических фигур применяются специальные формулы, с которыми мы с вами познакомимся в дальнейшем.
А теперь рассмотрим свойства площадей.
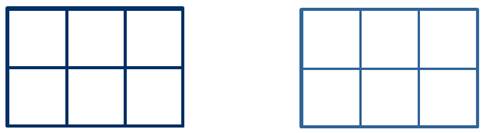
Возьмем два равных многоугольника.
Видим, что единица измерения площадей укладывается в них одинаковое число раз, а значит, равные многоугольники имеют равные площади.
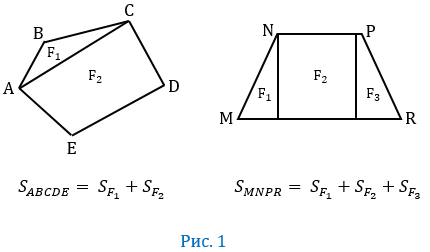
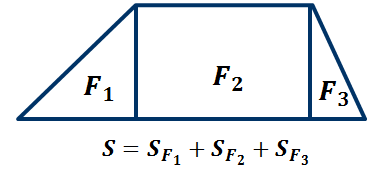
Следующий многоугольник состоит из трёх многоугольников, а тогда его площадь можно найти как сумму площадей фигур F1F2F3.
То есть, если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Рассмотренные два свойства являются основными свойствами площадей.
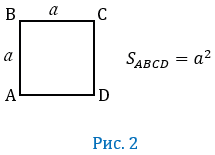
И ещё одно свойство: площадь квадрата равна квадрату его стороны. Если сторона квадрата равна 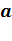
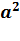
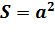
Действительно так. Давайте возьмем квадрат, сторона которого равна 3 сантиметра.
Также следует знать, что площадь всегда величина положительная.
Площади многоугольников
Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.
Свойства площади
1. Площадь любого многоугольника — величина положительная.
2. Равные многоугольники имеют равные площади.
3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Теорема: площадь прямоугольника
Доказательство
Определение
Теорема: площадь параллелограмма
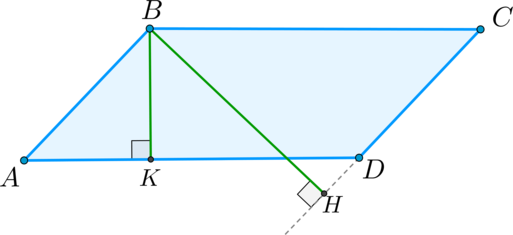
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Заметим, что прямоугольные треугольники \(ABB’\) и \(DCC’\) равны. Таким образом,
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
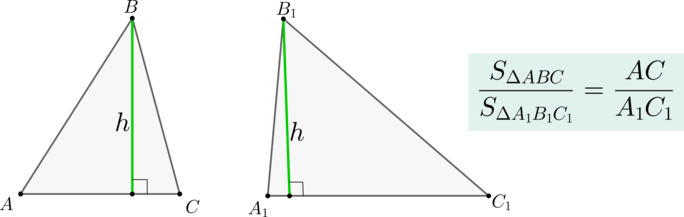
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_1B_1C_1\) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
Теорема
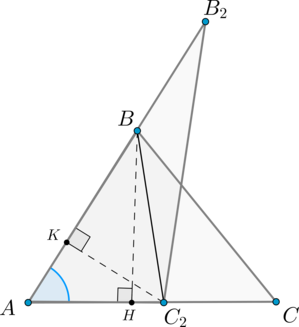
Если два треугольника \(\triangle ABC\) и \(\triangle A_2B_2C_2\) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
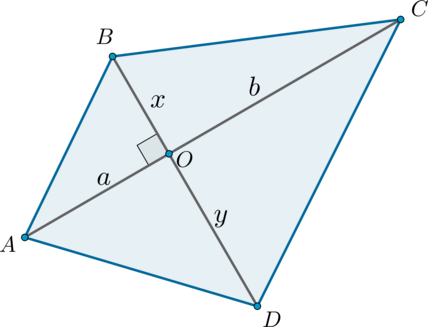
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
\(\begin
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: \[S_<\text<ромб>>=\dfrac12 d_1\cdot d_2\]
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
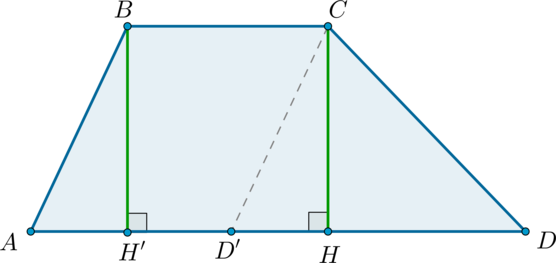
Теорема: площадь трапеции
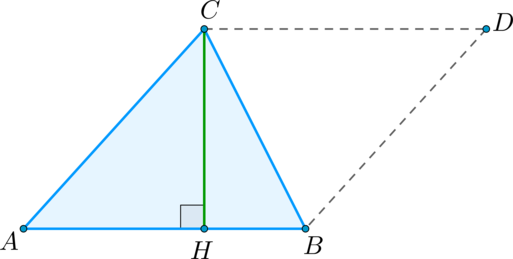
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
Тогда \(ABCD’\) – параллелограмм.
Проведем также \(BH’\perp AD, CH\perp AD\) ( \(BH’=CH\) – высоты трапеции).
Тогда \(S_
\[S_
Как найти площадь фигуры
Обозначение площади
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Если параметры фигуры переданы в разных единицах измерения длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Круг — это множество точек на плоскости, ограниченных окружностью, удаленных от центра на равном радиусу расстоянии. Радиусом принято называть отрезок, соединяющий центр с любой точкой окружности.
S = &pi × d 2 : 4;, где d — это диаметр.
S = L 2 : (4 × π), где L — это длина окружности.
Треугольник
Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, соединенных тремя отрезками. Эти три точки принято называть вершинами, а отрезки — сторонами. Рассчитать площадь треугольника можно несколькими способами по исходными данным, давайте их рассмотрим.
1. Если известна сторона и высота.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
2. Если известны две стороны и синус угла.
S = 0,5 × a × b * sinα, где a и b — две стороны, sinα — синус угла между ними.
3. Если есть радиус описанной окружности.
S = (a × b × с) : (4 × R), где a, b и с — стороны треугольника, а R — радиус описанной окружности.
4. Если есть радиус вписанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
У нас есть отличные онлайн-занятия с лучшими преподавателями по математике для учеников с 1 по 11 классы!
Прямоугольник
Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом. Узнать площадь прямоугольника помогут следующие формулы:
S = a × b, где a, b — длина и ширина прямоугольника.
Диагональ — это отрезок, который соединяет несмежные вершины многоугольника. Она есть во всех фигурах, число вершин которых больше трех.
S = 0,5 × d 2 × 𝑠𝑖𝑛(𝑎), где d — диагональ, α — угол между диагоналями.
Квадрат
Квадрат — это тот же прямоугольник, но при условии, что все его стороны равны. Найти его площадь легко:
S = d 2 : 2, где d — диагональ.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны и две не параллельны.
S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны под прямым углом.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны.
Ромб — это параллелограмм, у которого все стороны равны.
Расскажем про общие формулы расчета площади параллелограмма и ромба.
S = a × h, где a — сторона, h — высота.
S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
Для ромба: S = 0,5 × (d1 × d2), где d1, d2 — две диагонали. Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Площадь многоугольника
Одна из прикладных задач, которые решает геометрия — вычисление площадей многоугольников. Это необходимо строителям, земледельцам, конструкторам, летчикам, геологам. Даже в повседневной жизни знание формул, показывающих, как узнать площадь многоугольника, часто выручает при ремонте квартиры или дома.
Сначала определимся, что такое многоугольник, и что такое площадь. В геометрии многоугольником называют фигуру на плоскости, образованную замкнутой ломаной линией с количеством звеньев более 2-х. Это все известные и неизвестные нам фигуры, начиная от треугольника — квадрат, трапеция, ромб, шестиугольник, восьмиугольник и т.д. Готовые формулы, как найти площадь многоугольника созданы практически для каждой правильной фигуры с конечным количеством сторон. А вот что делать с неправильными?
Площади самых распространенных многоугольников можно найти по готовым формулам:
Правильным многоугольником называется фигура, у которой все стороны равны, а смежные углы одинаковые. Площадь — часть плоскости, в которой лежит фигура, заключенная между ее сторонами. Если многоугольник нарисован в тетради в клеточку, то площадь — это количество квадратиков внутри фигуры. За единицу площади принят квадратный метр (м 2 ), или квадратный сантиметр (см 2 ), в зависимости от размеров многоугольника.
Универсальный способ вычисления площади правильного многоугольника
Чтобы не запоминать десятки готовых формул, можно выучить только одну — как найти площадь многоугольника через периметр. Способ этот простой и не требует большого объема вычислений. Для работы нужны только линейка и карандаш.