Что такое площадь в геометрии

Площади геометрических фигур: список формул, описание, примеры

Содержание:

Для решения практических задач иногда приходится вычислять площади геометрических фигур. Они, например, нужны при измерениях земельных участков, поверхностей при проведении ремонтных и строительных работ. Рассмотрим, что такое площадь геометрической фигуры, по каким формулам она определяется в разных ситуациях.

Площади всех фигур в геометрии

Площадью называют численную характеристику поверхности, которая показывает сколько квадратов с размером 1 × 1 занимает объект на плоскости. Изменяется в квадратных единицах – метрах, сантиметрах, километрах и т. д.

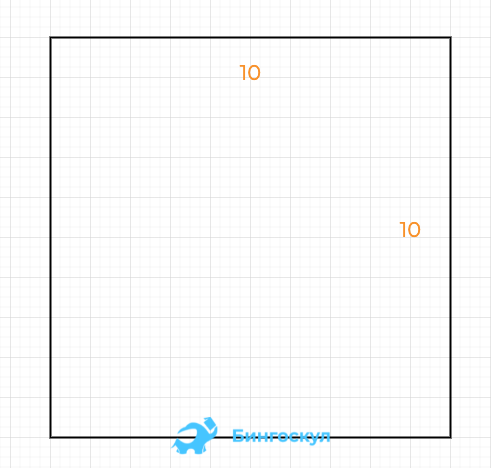
Для нарисованного по клеточкам четырёхугольника с прямыми углами это делается простым подсчётом с перемножением полученных значений. Для квадрата на примере это 100 см2: 10 × 10 см.

В математике насчитывается менее десятка фигур – замкнутых множеств, сформированных точками, площадь которых можно вычислить. Общий принцип расчётов сформирован благодаря интегральному счислению.

Формулы площадей фигур по геометрии

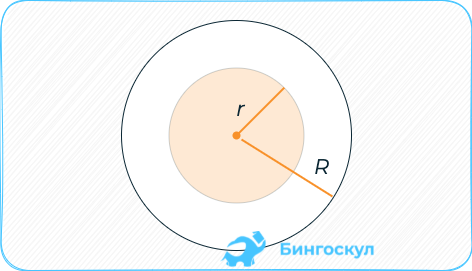
Если известен диаметр – четверти его квадрата на π.

Кольцо круга: разница между площадями кольца и круга.

Четырёхугольники

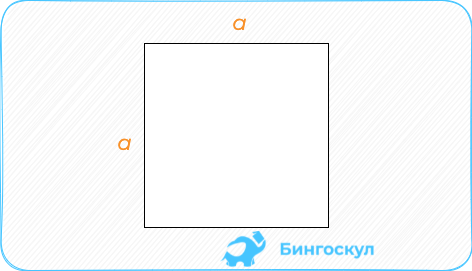
Квадрат: размеры сторон перемножаются.

Также площадь вычисляется как половина квадрата диагонали.

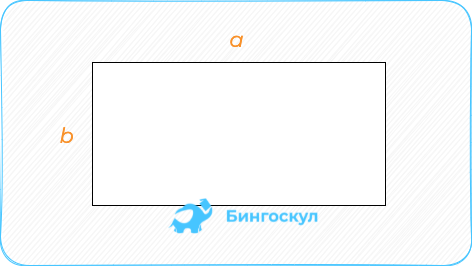
Прямоугольник: произведение соседних сторон – длины на ширину.

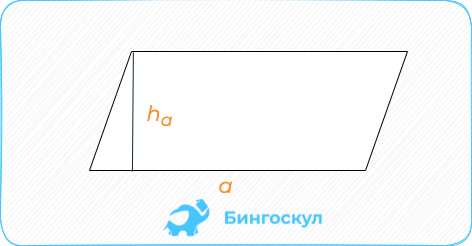
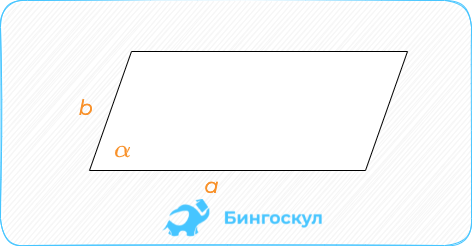
Параллелограмм: умножение длины стороны на опущенную к ней высоту.

Вторая формула применяется, когда известны длины сторон с углом между ними – произведение сторон на sin угла, под которым они пересекаются.

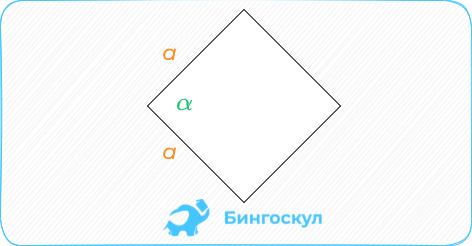
Ромб – параллелограмм с равными сторонами. Если известна сторона, площадь ромба вычисляется как произведение sin угла между сторонами на их длину в квадрате.

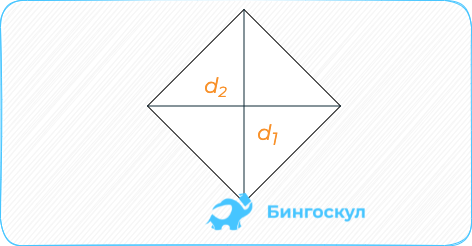
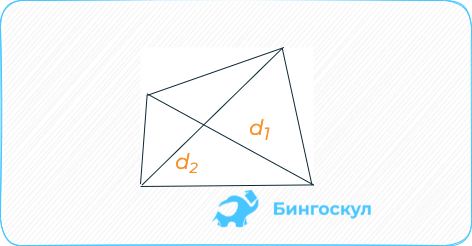
Если в задании даны длины диагоналей, площадь определяется как половина их произведения.

При наличии одной диагонали (полудиагонали) и стороны, неизвестные данные вычисляются по теореме Пифагора.

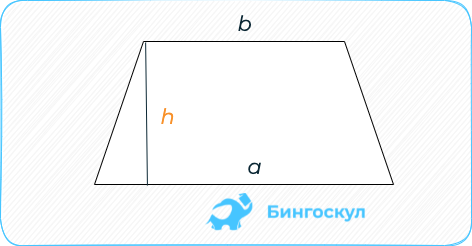
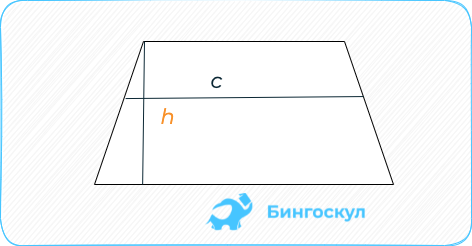
Трапеция: полусумма длин верхнего и нижнего оснований на высоту геометрической фигуры.

Когда даны средняя линия и высота, площадь находят путём перемножения их значений.

Выпуклый четырёхугольник: половина длины диагоналей, перемноженная на sin угла, который они образуют.

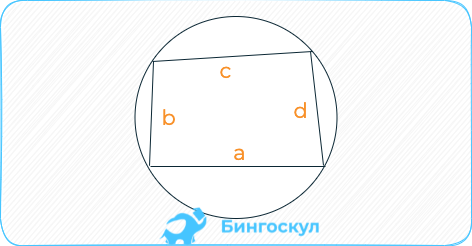
Вписанный в окружность 4-угольник: площадь вычисляется как корень квадратный из произведения разности периметра на длину каждой стороны.

В случае с прямоугольником, квадратом формула упрощается.

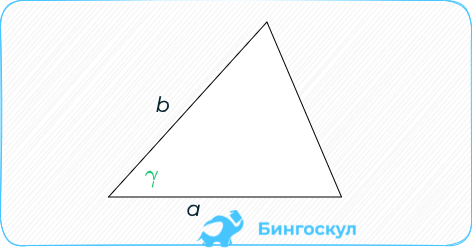
Треугольники

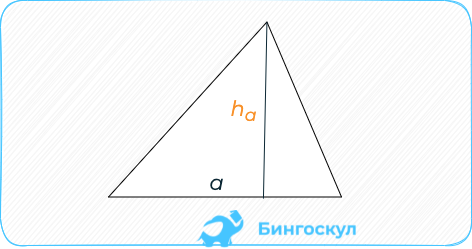
Половины стороны на проведённую к ней высоту.

Пары любых сторон на sin образуемого ими угла:

Квадрата полупериметра геометрической фигуры на тангенсы половин углов.

S = p 2 * tgα/2 * tgβ/2 * tgγ/2.

Корню квадратному произведения разницы полупериметров и сторон.

Квадрата длины стороны на синусы смежных углов, разделённому на удвоенный синус третьего, противоположного ей угла.

При известной высоте: отношению её произведения на синус угла, откуда та опущена, к двойному произведению синусов остальных углов.

Для прямоугольного 3-угольника, по сути, половины прямоугольника, применимо выражение:

Источник

Как найти площадь фигуры

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах измерения длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

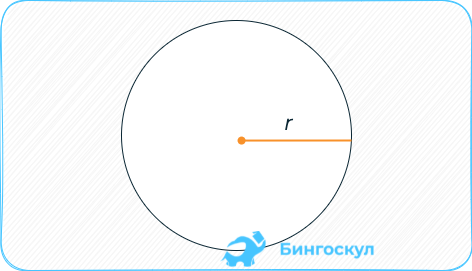
Круг — это множество точек на плоскости, ограниченных окружностью, удаленных от центра на равном радиусу расстоянии. Радиусом принято называть отрезок, соединяющий центр с любой точкой окружности.

S = &pi × d 2 : 4;, где d — это диаметр.

S = L 2 ​ : (4 × π), где L — это длина окружности.

Треугольник

Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, соединенных тремя отрезками. Эти три точки принято называть вершинами, а отрезки — сторонами. Рассчитать площадь треугольника можно несколькими способами по исходными данным, давайте их рассмотрим.

1. Если известна сторона и высота.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

2. Если известны две стороны и синус угла.

S = 0,5 × a × b * sinα, где a и b — две стороны, sinα — синус угла между ними.

3. Если есть радиус описанной окружности.

S = (a × b × с) : (4 × R), где a, b и с — стороны треугольника, а R — радиус описанной окружности.

4. Если есть радиус вписанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

У нас есть отличные онлайн-занятия с лучшими преподавателями по математике для учеников с 1 по 11 классы!

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом. Узнать площадь прямоугольника помогут следующие формулы:

S = a × b, где a, b — длина и ширина прямоугольника.

Диагональ — это отрезок, который соединяет несмежные вершины многоугольника. Она есть во всех фигурах, число вершин которых больше трех.

S = 0,5 × d 2 × 𝑠𝑖𝑛(𝑎), где d — диагональ, α — угол между диагоналями.

Квадрат

Квадрат — это тот же прямоугольник, но при условии, что все его стороны равны. Найти его площадь легко:

S = d 2 : 2, где d — диагональ.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны и две не параллельны.

S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны под прямым углом.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм, у которого все стороны равны.

Расскажем про общие формулы расчета площади параллелограмма и ромба.

S = a × h, где a — сторона, h — высота.

S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.

Для ромба: S = 0,5 × (d₁ × d₂), где d₁, d₂ — две диагонали. Для параллелограмма: S = 0,5 × (d₁ × d₂) × sinβ, где β — угол между диагоналями.

Источник

Площадь

Что такое площадь

Понятие площади фигур рассматривается одним из разделов математики — конкретно, геометрией. Результат решения задач с нахождением площади геометрических фигур может использоваться для решения математических задач, в быту, в производстве.

Площадь фигуры — численная характеристика, которая передает информацию о размере геометрической фигуры.

Фигура, в математическом мире определяемая как множество точек на плоскости, должна быть ограничена со всех сторон, чтобы иметь понятие площади. Если фигура располагается на одной плоскости, она не имеет объема, а только площадь.

В самом простом случае, площадь фигуры можно посчитать по количеству клеток, которые она занимает. Подобным способом можно легко посчитать площадь квадрата, прямоугольника или прямоугольного равнобедренного треугольника.

Площадь в геометрии обозначается знаком S, от английского square — площадь.

Как математическая характеристика, площадь имеет четыре характеристики:

Единицы измерения площади

Площадь фигуры может измеряться в разных единицах в зависимости от поверхности, на которой располагается. Основной системой измерения считается Международная система единиц СИ.

Площадь измеряется в единицах измерения в квадрате:

В Древней Руси употребляли такие величины, как квадратная верста, десятина, квадратный сажень.

В античных источниках единицей измерения площади были актус, арура, центурия, югер.

Формула нахождения площади в математике

Существует множество формул нахождения площади простых геометрических фигур, которые зависят, в основном, от количества углов, сторон и их соотношений.

Площадь прямоугольника

Прямоугольником является геометрическая фигура, все углы которой равны 90°. При этом таких углов должно быть, как минимум три, а четвертый будет равен 90° в силу закона о сумме углов четырехугольника в евклидовой геометрии.

Вычисление площади прямоугольника будет происходить через умножение сторон:

где a и b являются сторонами прямоугольника.

Площадь квадрата

Квадратом является прямоугольник с равными сторонами. Все его углы равны 90°. Площадь квадрата можно найти сразу двумя способами:

По длине стороны:

Через диагонали:

где a — длина сторон квадрата;

d — длина диагоналей квадрата.

Площадь круга

Кругом является часть плоскости, которая лежит внутри окружности. Круг не имеет ни одного угла, а точки его окружности находятся на равном удалении от центра.

Площадь круга можно найти двумя способами:

Через радиус:

где π — постоянная Пи, равна 3,14.

Радиус, упоминаемый в формуле, является линией или отрезком, соединяющим центр и любую из точек окружности.

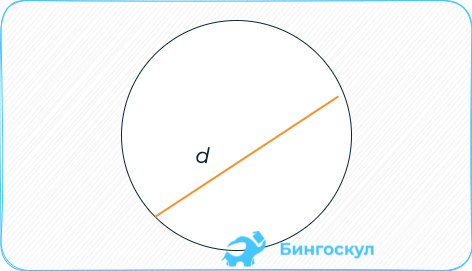
Через диаметр:

где π — постоянная Пи, равна 3,14.

Диаметр является отрезком, соединяющим две точки окружности и проходящим через центр. Он включает в себя два противоположно направленных радиуса.

Площадь эллипса

Эллипс является частным случаем окружности. Он, так же, как и круг, не имеет ни одного угла, но при этом точки окружности находятся на разном удалении от центра.

Найти площадь эллипса можно только одним способом: через произведение длин большой и малой полуосей эллипса и числа пи.

Площадь эллипса находится через произведение длин большой и малой полуосей эллипса и числа пи:

Площадь параллелограмма

Параллелограмм является геометрической фигурой с 4 углами и 4 сторонами, однако он отличается от прямоугольника по строению. Его противолежащие стороны попарно параллельны, а углы равны зеркально противолежащим.

Частными случаями параллелограмма являются квадрат, прямоугольник и ромб.

Найти площадь параллелограмма можно тремя способами:

Через сторону и высоту:

где a — сторона, к которой проведена высота,

h — высота непосредственно.

Через две стороны и величину угла между ними:

Через диагонали и угол между ними:

S = 1 2 × d 1 × d 2 × sin y

где d 1 и d 2 — это диагонали параллелограмма,

y — угол между ними.

Площадь ромба

Ромб, как частный случай параллелограмма, имеет те же свойства, кроме того, что все его стороны равны.

Площадь ромба также можно найти тремя способами:

По длине стороны и высоте:

Формула площади ромба по стороне и высоте выглядит так же, как и площадь параллелограмма по таким же характеристикам, с условием, что все высоты ромба будут равны:

По длине стороны и углу:

Формула площади ромба через длину сторон и углу между ними похожа на соответствующую формулу площади параллелограмма с условием того, что стороны равны, а значит, их перемножение можно заменить квадратом величины стороны:

По длине его диагоналей:

Площадь трапеции

Трапеция отличается от всех предыдущих фигур тем, что только две ее стороны, боковые, могут быть равны между собой. При этом они не параллельны. Две другие стороны параллельны, но не равны. Сумма углов трапеции равна 360°.

Площадь трапеции можно найти двумя способами:

По формуле Герона:

По длине основ и высоте:

Площадь треугольника

Треугольник является геометрической фигурой с тремя сторонами и суммой углов, равной 180°. По величине углов треугольники делятся на острые, тупые и прямоугольные. По числу равных сторон треугольники делятся на разносторонние, равносторонние и равнобедренные.

Площадь треугольника можно найти множеством способов:

По гипотенузе и острому углу:

a — любой из прилежащих острых углов.

Через сторону и высоту:

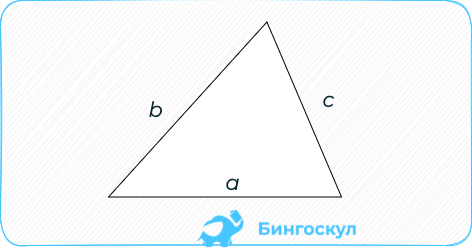
Через три стороны:

где р — полупериметр.

Через две стороны и угол между ними:

S = 1 2 × a × b × sin y

Через три стороны и радиус описанной окружности:

Через три стороны и радиус вписанной окружности:

где р — полупериметр.

Пояснения на примерах

Стены класса равны 7 и 5 метрам. Чему будет равна площадь пола в данной комнате?

Решение: S = 7 × 5 = 35

Ткань летучего змея порвалась. Вася решил сделать новую форму. Он посчитал, что длина жердей летучего змея равна 15 и 23 см. Форму какой площади нужно взять Васе с учетом того, что для припусков для пришивания нужно взять еще 2 см?

Равнобедренный треугольник имеет основание 4 дм и высоту 7 дм. Сколько будет его площадь?

Источник

Площадь (геометрия)

Площадь — величина, определяющая размер поверхности, одно из основных свойств геометрических фигур. Исторически, вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Площадь несложных геометрических фигур определяют, подсчитывая количество единичных квадратов, которыми фигуры можно покрыть.

Площадь принято обозначать большой латинской буквой S, в англоязычной литературе — буквой A от англ. area.

Содержание

[править] Формальное определение

Площадью в планиметрии может называться любая величина, удовлетворяющая условиям:

Для фигур на плоскости, не состоящих из целого числа единичных квадратов, а также для трехмерных поверхностей, площадь определяется с помощью предельного перехода и может быть вычислена с помощью интегрирования.

[править] Площадь в аналитической геометрии

Аналитическая геометрия позволяет решать геометрические задачи алгебраическими методами, оперируя такими понятиями как система координат, вектор. Плоскость в трехмерном пространстве имеет две поверхности. Площади двух поверхностей обозначаются с противоположными знаками. Поскольку ориентация поверхности задается вектором нормали к ней, то площадь тоже определяют как вектор, коллинеарной нормали к поверхности.

При изменении порядка множителей в этой формуле, [math] \mathbf [/math] меняет знак, соответствующий нормалям для двух разных сторон поверхности. Как произведение двух векторов [math] \mathbf [/math] является псевдовектором — при изменении направления каждого из векторов [math] \mathbf [/math] и [math] \mathbf [/math] на противоположный, [math] \mathbf [/math] направление не меняет.

Источник

ПЛОЩАДЬ (в геометрии)

Смотреть что такое «ПЛОЩАДЬ (в геометрии)» в других словарях:

Площадь (в геометрии) — Площадь, одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П. было уже в древности… … Большая советская энциклопедия

Площадь (в геометрии) — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

Площадь — часть поверхности, ограниченная каким либо замкнутымконтуром. Величина П. выражается числом заключающихся в ней квадратныхединиц. Вычисление П. производится с помощью приемов, излагаемых вгеометрии и приложении интегрального исчисления к… … Энциклопедия Брокгауза и Ефрона

ГЕОМЕТРИИ ОБЗОР — Геометрия раздел математики, тесно связанный с понятием пространства; в зависимости от форм описания этого понятия возникают различные виды геометрии. Предполагается, что читатель, приступая к чтению этой статьи, обладает некоторыми… … Энциклопедия Кольера

Площадь — I Площадь одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П.… … Большая советская энциклопедия

площадь — сущ., ж., употр. часто Морфология: (нет) чего? площади, чему? площади, (вижу) что? площадь, чем? площадью, о чём? о площади; мн. что? площади, (нет) чего? площадей, чему? площадям, (вижу) что? площади, чем? площадями, о чём? о площадях 1.… … Толковый словарь Дмитриева

ПЛОЩАДЬ — численная характеристика, приписываемая плоским фигурам определенного класса (напр., многоугольникам) и обладающая следующими свойствами: 1) П. неотрицательна; 2) П. аддитивна (в случае многоугольников это означает, что если фигура составлена из… … Математическая энциклопедия

Площадь — часть поверхности, ограниченная каким либо замкнутым контуром. Величина П. выражается числом заключающихся в ней квадратных единиц. Вычисление П. производится с помощью приемов, излагаемых в геометрии и приложения интегрального исчисления к… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

НЕЕВКЛИДОВЫ ГЕОМЕТРИИ — в буквальном понимании все геометрич. системы, отличные от геометрии Евклида; однако обычно термин Н. г. применяется лишь к геометрич. системам (отличным от геометрии Евклида), в к рых определено движение фигур, причем с той же степенью свободы,… … Математическая энциклопедия

Неевклидовы геометрии — в буквальном понимании все геометрические системы, отличные от геометрии Евклида; однако обычно термин «Н. г.» применяется лишь к геометрическим системам (отличным от геометрии Евклида), в которых определено движение фигур, причём с той… … Большая советская энциклопедия

Источник