Что такое погрешность результата измерения в метрологии

Погрешность измерений

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

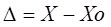
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

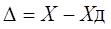
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

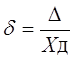
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

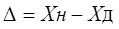
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

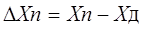
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

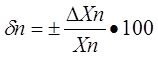
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

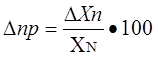
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Источник

Погрешность измерений. Классификация

Погрешность средств измерения и результатов измерения.

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Инструментальные и методические погрешности.

Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Систематическая и случайная погрешности.

Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Причинами возникновения систематических составляющих погрешности измерения являются:

Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.

Погрешности адекватности и градуировки.

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

Абсолютная, относительная и приведенная погрешности.

Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.

Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.

Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

Аддитивные и мультипликативные погрешности.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).

Источник

Погрешности измерений и их классификация

Полученное из опыта значение измеряемой величины может отличаться от ее действительного (истинного) значения.

Погрешность измерения – отклонение результата измерения от истинного (действительного) значения измеряемой величины.

Это может быть обусловлено конструктивными недостатками прибора, несовершенством технологии его изготовления, а также влиянием различных внешних факторов.

Таким образом, погрешности классифицируют:

По источнику возникновения (метод, инструмент, субъект)

-Методические (зависят от метода измерения и способа включения приборов в электрическую цепь)

-Инструментальные (зависят от средства измерения)

-Субъективные (зависят от измерителя)

По условиям проведения измерений (температура, давление, влажность)

-Дополнительные (условия отличны от нормальных)

По характеру проявления (систематические, случайные, промахи)

Систематические – погрешности, остающиеся постоянными или закономерно изменяющимися при повторных измерениях тем же способом и средствами. Т.е. они заранее известны и их легко исключить.

Случайные – погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Обычно выявляются в результате многократных измерений (не менее 10).

Промах – грубая ошибка, обусловленная неправильным отсчетом или расчетом, небрежностью измеряющего, поломки прибора, неправильно собранной схемы, невнимательности и т.д. Такие данные необходимо исключать.

По временному поведению измеряемой величины (статическая, динамическая)

Статическая – когда измеряемая величина не меняется за время измерения

Динамическая – когда прибор не успевает реагировать на изменения измеряемой величины.

По способу выражения измеряемой величины

Абсолютной погрешностью D Х называется разность между измеренным и действительным значениями.

– действительное значение измеряемой величины.

Выражается D Х в единицах измеряемой величины.

Относительная погрешность – отношение абсолютной погрешности к действительному значению измеряемой величины.

Выражается в процентах или относительных единицах. Относительная погрешность характеризует точность измерений.

Приведенная погрешность g _пр – отношение абсолютной погрешности к номинальному (нормированному) значению – верхнему пределу диапазона или поддиапазона измерения прибора.

Пределом измерения прибора называется наибольшая величина, на которую рассчитан данный прибор.

Прибор может иметь несколько пределов измерений (например, вольтметр).

Чем меньшую погрешность дает прибор, тем он точнее.

Выражается в процентах.

Максимальная приведенная погрешность определяет класс точности прибора.

Электроизмерительные приборы изготавливаются нескольких классов точности

Источник

Неопределенность измерений в метрологии

Определения погрешности и неопределенности измерений.

История возникновения термина «неопределенность измерений».

Термины используемые при расчете неопределенности.

Соотношение терминов теории неопределенности с терминами классической теории точности (в скобках):

Подробно о типах определённости и их расчётах рассказано в статье «Понятие и типы неопределенностей. ГОСТ 34100.3-2017»

Оценка результата измерений в терминах «погрешность измерений».

Рис.1. Диапазон возможных значений при погрешности

Оценка результата измерений в терминах «неопределенность измерений».

Рис.2. Диапазон возможных значений при неопределенности

Рис.3. Интервал значений при расчете неопределенности

Расчёт неопределённости с применением приборов.

В следующей статье «Расчет неопределенности результатов измерений | пример для люксметра «еЛайт»» мы рассмотрим практический пример как вручную вычислить неопределенность измерений освещенности, используя люксметр-пульсметр-яркомер еЛайт02. В некоторых современных приборах такой расчёт неопределённости уже осуществляется автоматически, как, например, в самом доступном люксметре с поверкой еЛайт-мини.

Рис.4. Профессиональный измеритель освещённости еЛайт01 с функцией автоматического расчёта неопределённости измерений.

Рис.5. Термоанемометр-гигрометр-барометр ЭкоТерма Максима 01 с функцией автоматического расчёта неопределённости измерений.

Выводы.

Отличие понятия «погрешности» от «неопределенности»:

Понравился материал? Поделитесь им в соцсетях:

Источник

Что есть погрешность средства измерений и можно ли ее «измерить»?

А.А. Данилов.
ОБУ «Пензенский ЦСМ»,
Россия, г.Пенза, pcsm@sura.ru

Е.Ю. Лукашов.
Федеральное государственное унитарное предприятие «Всероссийский чно-исследовательский институт метрологической службы» (ФГУП ИИМС»),
Москва, Россия, e-mail: sva@vniims.ru

Ключевые слова: погрешность средств измерений, случайные величины, характеристики погрешности.

This article describes the questions of a measurability of the inaccuracy of a measuring instrument. It gives an explanation that the inaccuracy is a random quantity and it cannot be a constant value. It is only possible to determine the characteristics of the inaccuracy.

Key words: inaccuracy of a measuring instruments, random variables, inaccuracy characteristics.

Мое дело сказать правду, а не заставлять верить в нее.
Жан Жак Руссо

РМГ 29-99 ГСП. Метрология. Термины и определения

Поводом для написания настоящей статьи послужило распространенное в последнее время заблуждение (приверженцами которого являются не только начинающие метрологи, но и некоторые метрологи со стажем), основанное на неправильном толковании определения погрешности средства измерений (СИ), приведённом в РМГ 29-99 [1]:

Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением», т.е.

Используя указанное определение, оппоненты считают, что при проведении поверки СИ, эталон выбран правильно, следовательно, его погрешностью, в сравнении с погрешностью поверяемого СИ, можно пренебречь. Это дает возможность получить погрешность СИ, вычислив разность «между показанием СИ и действительным значением измеряемой физической величины».

Где здесь противоречие?

Во-первых, в правой части формулы (1) обе величины являются случайными. Поэтому и погрешность тоже является случайной величиной. А, следовательно, можно говорить об отдельной реализации случайной величины. Если же говорить о погрешности вообще, то её оценку необходимо рассматривать, как оценку одной или нескольких характеристик случайной величины.

В-третьих, используя один экземпляр эталона и выполнив необходимые измерения, можно получить одно значение ε₁, погрешности СИ в проверяемой точке диапазона его измерений. Используя же другой экземпляр эталона, также выполнив необходимые измерения, можно получить второе значение ε₂ погрешности СИ. Для n-го экземпляра эталона будет получено n-е значение ε_n погрешности СИ. Какое из них принять за погрешность СИ?

Почему такое возможно? Потому, что каждый из экземпляров эталонов хранит, воспроизводит и передает свое значение единицы величины, которое отличается от номинального значения и находится в некоторых допускаемых пределах отклонения от него.

Те же рассуждения можно повторить в отношении повторных экспериментов с тем же эталоном и в той же точке диапазона измерений и в отношении других точек диапазона измерений СИ.

И, наконец, в-четвертых, если бы кому-нибудь удалось получить истинную погрешность СИ, тогда этот уникальный человек смог бы определить истинное значение измеряемой величины. Возможно ли такое?

Во-первых, при повторении эксперимента в силу случайных причин, устранить которые (либо свести к нулю их влияние) не представляется возможным, будут зафиксированы показания СИ, в общем случае отличающиеся между собой. На этом основании Шишкин И.Ф. в предложенной им аксиоматике формулирует третью аксиому метрологии, согласно которой «результат измерения без округления является случайным» [3]. Из этой аксиомы следует, что результат измерения имеет вполне конкретное значение, которое следует рассматривать, как реализацию случайной величины.

Во-вторых, действительное значение измеряемой величины, приписанное эталону, при его воспроизведении в силу случайных причин в действительности также не постоянно. Кроме того, это действительное значение также неизвестно абсолютно точно, в том числе и для первичного эталона. Именно поэтому для эталонов регламентируют неисключенную систематическую погрешность, случайную погрешность и нестабильность [4].

Рассмотрим теперь следующий тезис оппонентов, утверждающих, что погрешность можно измерить.

Из этого определения следует, что

— во-первых, измерению подлежит величина,

— во-вторых, техническое средство предназначенное для измерения должно хранить единицу величины.

— в-третьих, в результате рений получают оценку значения величины.

Так можно ли говорить об изме рении погрешности?

Нет! Погрешность измерить невозможно! Можно лишь говорить об определении характеристик погрешности [5].

Погрешность измерить невозможно. Можно определить лишь характеристики погрешности

ВЫВОДЫ

2. Погрешность измерить невозможно. Можно определить лишь характеристики погрешности.

1. РМГ 29-99. ГСИ. Метрология. Основные термины и определения.

2. Установка для поверки вольтметров В1-8. Техническое описание и инструкция по эксплуатации,- С. 31.

3. Шишкин И. Ф. Теоретическая метрология. Часть 1. Общая теория измерений. Учебник для вузов.-СПб.: Питер,- 2010.- С. 52.

4. ГОСТ8.381-2009. ГСИ. Эталоны. Способы выражения точности.

5. МИ 1317-2004. ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров.

Источник