Что такое принцип неопределенности
Принцип неопределенности Гейзенберга в квантовой механике
Обновлено: 19 Июня 2021
Разбираем принцип неопределенности Гейзенберга с пояснениями и примерами.
Что такое принцип неопределенности Гейзенберга
Если говорить простым языком, это фундаментальный закон квантовой механики, который гласит, что невозможно точно определить скорость и местонахождение частицы.

Источник: userapi.com
Если обратиться к Википедии, там мы увидим определение: «соотношение неопределенностей, устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых, описываемых некоммутирующими операторами». Чем точнее можно рассмотреть одну характеристику частицы, тем хуже получится рассмотреть вторую. То есть чем точнее определяются координаты частицы, тем неопределеннее становится ее импульс. Точно так и наоборот.
В чем заключается сущность и смысл
Легче всего этот принцип можно представить с помощью примера. Представим, что электрон — это баскетбольный мяч, а фотоны — это бильярдные шары. За счет фотонов мы видим мир и расположение объектов на том или ином месте. Происходит это, когда фотоны отскакивают от объекта и попадают к нам в глаз (проще говоря, это свет).
Так вот, кидая бильярдные шары в баскетбольный мяч, мы будем следить за шарами, которые отскакивают, чтобы понять его местонахождение. Вот только шары довольно тяжелые относительно баскетбольного мяча, поэтому каждый раз будут придавать ему импульс, и тот будет отдаляться. Таким образом, чем сильнее мы пытаемся определить местоположение электрона, тем усиленнее кидаем в него фотоны и ненароком двигаем.
По принципу неопределенности Гейзенберга ни один доступный сегодня метод определения положения электрона не пройдет бесследно для импульса, и мы не сможем определить оба фактора одновременно.
Формула выглядит следующим образом:
\(ħ\) — постоянная Планка;
\(Δx\) — среднеквадратическое отклонение координаты;
\(Δp\) — среднеквадратическое отклонение импульса.
Необычные последствия соотношения неопределенностей
«Отсутствие покоя»
Это состояние с наименьшей энергией. Как вам уже известно из уроков физики, полная энергия частицы складывается из кинетической и потенциальной E=p²/2m+U⃗(r). Состояние с наиболее низким энергетически запасом соответствует нахождению частицы в минимуме потенциальной энергии с нулевым импульсом. Но это противоречит соотношению неопределенностей, так как оказываются точно заданы координата и импульс. Поэтому в квантовой задаче, в состоянии самой низкой возможной энергии, частица должна иметь «слегка» неопределенную координату и «слегка» неопределенный импульс. Легче представить это как дрожание частицы рядом с положением равновесия. Однако подобная аналогия условна, так как мы рассматриваем исключительно квантовый эффект делокализации частицы.
Нулевые колебания гармонического осциллятора
Из-за условного дрожания частицы рядом с положением равновесия делокализацию квантовой частицы в ее основном состоянии (состояние с наиболее низкой энергией) называют «нулевыми колебаниями».
При точном решении задач об уровнях гармонического осциллятора появляется еще половина кванта энергии, из-за чего уравнение выглядит следующим образом: \(E=ħ\omega(n+1/2).\)
Размах делокализации частицы в пространстве называют амплитудой нулевых колебаний. Можно ее оценить для гармонического осциллятора.
Квантовые кристаллы гелия
Очевидно, что амплитуда нулевых колебаний больше, если легче атомы. А чем она больше, тем слабее воздействие между ними. В пример можно привести кристаллы, которые формируются при экстремально низких температурах из атомов гелия. Эти атомы в четыре раза легче кислорода и очень слабо взаимодействуют друг с другом, так как являются инертными. В том случае амплитуда нулевых колебаний близка к межатомному расстоянию. Из-за такой делокализации атомов кристалл не держится: жидкий гелий не замерзает при температурах до абсолютного нуля. Чтобы стабилизировать жесткую фазу, нужно ко всему прочему приложить давление в
Остались вопросы? Ленитесь разобраться в сложной теме? Заходи на сервис ФениксХелп. Лучшие специалисты помогут решить любую задачу, написать контрольную, курсовую или дипломную работу любой сложности.
Принцип неопределённости Гейзенберга
| Основа |
|---|
| Классическая механика · Интерференция · Бра и кет · Гамильтониан |
| Фундаментальные понятия |
|---|
| Квантовое состояние · Волновая функция · Суперпозиция · Запутанность · Измерение · Неопределённость · Запрет Паули · Дуализм · Декогеренция · Теорема Эренфеста · Туннелирование |
| Эксперименты |
|---|
| Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга · Проверка неравенств Белла · Фотоэффект · Эффект Комптона |
| Формулировки |
|---|
| Картина Шрёдингера · Картина Гейзенберга · Картина взаимодействия · Матричная квантовая механика · Интегралы по траекториям |
| Уравнения |
|---|
| Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака |
| Интерпретации |
|---|
| Копенгагенская интерпретация · Теория скрытых параметров · Многомировая |
| Сложные темы |
|---|
| Квантовая теория поля · Квантовая гравитация · Теория всего |
| Известные учёные |
|---|
| Планк · Эйнштейн · Шрёдингер · Гейзенберг · Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт |
Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) — в квантовой механике так называют принцип, дающий нижний (ненулевой) предел для произведения дисперсий величин, характеризующих состояние системы.
Обычно принцип неопределённости иллюстрируется следующим образом. Рассмотрим ансамбль невзаимодействующих эквивалентных частиц, приготовленных в определённом состоянии, с каждой из которых производятся два последовательных измерения. Первое определяет импульс частицы, а второе, сразу после этого, её координату. Измерение импульса даст некоторое распределение с характерной дисперсией. Второе же измерение даст распределение значений, дисперсия которого 


В общем смысле, соотношение неопределённости возникает между любыми переменными состояния, определяемыми некоммутирующими операторами. Это — один из краеугольных камней квантовой механики, который был открыт Вернером Гейзенбергом в 1927 г. [ источник? ]
Содержание
Краткий обзор
Принцип неопределённости в квантовой механике иногда объясняется таким образом, что измерение координаты обязательно влияет на импульс частицы. По-видимому, сам Гейзенберг предложил это объяснение, по крайней мере первоначально. То, что влияние измерения на импульс несущественно, может быть показано следующим образом: рассмотрим ансамбль (невзаимодействующих) частиц приготовленных в одном и том же состоянии; для каждой частицы в ансамбле мы измеряем либо импульс, либо координату, но не обе величины. В результате измерения мы получим, что значения распределены с некоторой вероятностью, и для дисперсий dp и dq верно отношение неопределённости.
Соответственно, любая частица (в общем смысле, например несущая дискретный электрический заряд) не может быть описана одновременно как «классическая точечная частица» и как волна. (Сам факт того, что какое-либо из этих описаний может быть справедливо, по крайней мере в отдельных случаях, называют корпускулярно-волновым дуализмом ). Принцип неопределённости, в виде, первоначально предложенном Гейзенбергом, верен в случае, когда ни одно из этих двух описаний не является полностью и исключительно подходящим, например частица в коробке с определённым значением энергии; то есть для систем, которые не характеризуются ни каким-либо определённым «положением» (какое-либо определённое значение расстояния от потенциальной стенки), ни каким-либо определённым значением импульса (включая его направление).
Существует точная, количественная аналогия между отношениями неопределённости Гейзенберга и свойствами волн или сигналов. Рассмотрим переменный во времени сигнал, например звуковую волну. Бессмысленно говорить о частотном спектре сигнала в какой-либо момент времени. Для точного определения частоты необходимо наблюдать за сигналом в течение некоторого времени, таким образом теряя точность определения времени. Другими словами, звук не может иметь и точного значения времени, как например короткий импульс, и точного значения частоты, как, например, в непрерывном чистом тоне. Временно́е положение и частота волны во времени походят на координату и импульс частицы в пространстве.
Определение
Если приготовлены несколько идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину стандартного отклонения Δx координаты и стандартного отклонения Δp импульса, мы найдем что:

где 
В повседневной жизни мы обычно не наблюдаем неопределённость потому, что значение h чрезвычайно мало.
Другие характеристики
Было развито множество дополнительных характеристик, включая описанные ниже:
Выражение конечного доступного количества информации Фишера
Обобщённый принцип неопределённости
Принцип неопределённости не относится только к координате и импульсу. В своей общей форме, он применим к каждой паре сопряжённых переменных. В общем случае, и в отличие от случая координаты и импульса, обсуждённого выше, нижняя граница произведения неопределённостей двух сопряжённых переменных зависит от состояния системы. Принцип неопределённости становится тогда теоремой в теории операторов, которую мы здесь приведем
Теорема. Для любых самосопряжённых операторов : A:H → H и B:H → H, и любого элемента x из H такого, что A B x и B A x оба определены (то есть, в частности, A x и B x также определены), имеем:
Следовательно, верна следующая общая форма принципа неопределённости, впервые выведенная в 1930 г. Говардом Перси Робертсоном и (независимо) Эрвином Шрёдингером :
Это неравенство называют отношением Робертсона — Шрёдингера.
Оператор AB—BA называют коммутатором A и B и обозначают как [A,B]. Он определен для тех x, для которых определены оба ABx и BAx.
Из отношения Робертсона — Шрёдингера немедленно следует отношение неопределённости Гейзенберга:
Предположим, A и B — две переменные состояния, которые связаны с самосопряжёнными (и что важно — симметричными) операторами. Если ABψ и BAψ определены, тогда:

среднее значение оператора переменной X в состоянии ψ системы, и:
оператор стандартного отклонения переменной X в состоянии ψ системы
Возможно также существование двух некоммутирующих самосопряжённых операторов A и B, которые имеют один и тот же собственный вектор ψ. В этом случае ψ представляет собой чистое состояние, которое является одновременно измеримым для A и B.
Общие наблюдаемые переменные, которые повинуются принципу неопределённости
Предыдущие математические результаты показывают, как найти отношения неопределённости между физическими переменными, а именно, определить значения пар переменных A и B коммутатор которых имеет определённые аналитические свойства.
Интерпретации
Альберту Эйнштейну принцип неопределённости не очень понравился, и он бросил вызов Нильсу Бору и Вернеру Гейзенбергу известным мысленным экспериментом (См. дебаты Бор-Эйнштейн для подробной информации): заполним коробку радиоактивным материалом, который испускает радиацию случайным образом. Коробка имеет открытый затвор, который немедленно после заполнения закрывается при помощи часов в определённый момент времени, позволяя уйти небольшому количеству радиации. Таким образом время уже точно известно. Мы все ещё хотим точно измерить сопряжённую переменную энергии. Эйнштейн предложил сделать это, взвешивая коробку до и после. Эквивалентность между массой и энергией по специальной теории относительности позволит точно определить, сколько энергии осталось в коробке. Бор возразил следующим образом: если энергия уйдет, тогда полегчавшая коробка сдвинется немного на весах. Это изменит положение часов. Таким образом часы отклоняются от нашей неподвижной системы отсчёта, и по специальной теории относительности, их измерение времени будет отличаться от нашего, приводя к некоторому неизбежному значению ошибки. Детальный анализ показывает, что неточность правильно дается соотношением Гейзенберга.
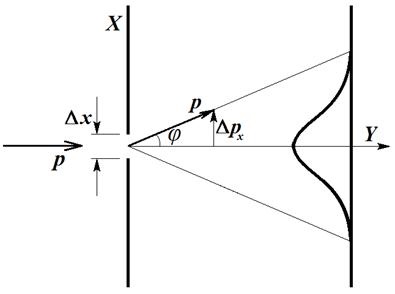
В пределах широко, но не универсально принятой Копенгагенской интерпретации квантовой механики, принцип неопределённости принят на элементарном уровне. Физическая вселенная существует не в детерминистичной форме, а скорее как набор вероятностей, или возможностей. Например, картина (распределение вероятности) произведённая миллионами фотонов, дифрагирующими через щель может быть вычислена при помощи квантовой механики, но точный путь каждого фотона не может быть предсказан никаким известным методом. Копенгагенская интерпретация считает, что это не может быть предсказано вообще никаким методом.
Эйнштейн был убеждён, что эта интерпретация была ошибочной. Его рассуждение основывалось на том, что все уже известные распределения вероятности являлись результатом детерминированных событий. Распределение подбрасываемой монеты или катящейся кости может быть описано распределением вероятности (50 % орёл, 50 % решка). Но это не означает, что их физические движения непредсказуемы. Обычная механика может вычислить точно, как каждая монета приземлится, если силы, действующие на неё будут известны, а орлы/решки будут все ещё распределяться случайно (при случайных начальных силах).
Эйнштейн предполагал, что существуют скрытые переменные в квантовой механике, которые лежат в основе наблюдаемых вероятностей.
Ни Эйнштейн, ни кто-либо ещё с тех пор не смог построить удовлетворительную теорию скрытых переменных, и неравенство Белла иллюстрирует некоторые очень тернистые пути в попытке сделать это. Хотя поведение индивидуальной частицы случайно, оно также скоррелировано с поведением других частиц. Поэтому, если принцип неопределённости — результат некоторого детерминированного процесса, то получается, что частицы на больших расстояниях должны немедленно передавать информацию друг другу, чтобы гарантировать корреляции в своём поведении.
Принцип неопределённости в популярной культуре
Принцип неопределённости часто неправильно понимается или приводится в популярной прессе. Одна частая неправильная формулировка в том, что наблюдение события изменяет само событие. Это может быть верным в некоторых случаях для некоторых событий, но это не имеет никакого отношения к принципу неопределённости в квантовой механике.
Другие (также вводящие в заблуждение) аналогии с макроскопическими эффектами были предложены для объяснения принципа неопределённости: одна из них рассматривает придавливание арбузной семечки пальцем. Эффект известен — нельзя предсказать, как быстро или куда семечка исчезнет. Этот случайный результат базируется полностью на хаотичности, которую можно объяснить в простых классических терминах.
В некоторых научно-фантастических рассказах устройство для преодоления принципа неопределённости называют компенсатором Гейзенберга, наиболее известное используется на звездолёте «Энтерпрайз» из фантастического телесериала Звёздный Путь в телепортаторе. Однако, неизвестно, что означает «преодоление принципа неопределённости». На одной из пресс-конференций продюсера сериала спросили «Как работает компенсатор Гейзенберга?», на что он ответил «Спасибо, хорошо!».
Научный юмор
Необычная природа принципа неопределённости Гейзенберга и его запоминающееся название, сделали его источником нескольких шуток. Говорят, что популярной надписью на стенах физического факультета университетских городков является: «Здесь, возможно, был Гейзенберг».
В другой шутке о принципе неопределённости, квантового физика останавливает на шоссе полицейский и спрашивает: «Вы знаете, как быстро Вы ехали, сэр?». На что физик отвечает: «Нет, но я точно знаю, где я!»
Литература
Использованная литература
Журнальные статьи
Внешние ссылки
См. также
Принцип неопределенности Гейзенберга
Невозможно одновременно с точностью определить координаты и скорость квантовой частицы.
В обыденной жизни нас окружают материальные объекты, размеры которых сопоставимы с нами: машины, дома, песчинки и т. д. Наши интуитивные представления об устройстве мира формируются в результате повседневного наблюдения за поведением таких объектов. Поскольку все мы имеем за плечами прожитую жизнь, накопленный за ее годы опыт подсказывает нам, что раз всё наблюдаемое нами раз за разом ведет себя определенным образом, значит и во всей Вселенной, во всех масштабах материальные объекты должны вести себя аналогичным образом. И когда выясняется, что где-то что-то не подчиняется привычным правилам и противоречит нашим интуитивным понятиям о мире, нас это не просто удивляет, а шокирует.
В первой четверти ХХ века именно такова была реакция физиков, когда они стали исследовать поведение материи на атомном и субатомном уровнях. Появление и бурное развитие квантовой механики открыло перед нами целый мир, системное устройство которого попросту не укладывается в рамки здравого смысла и полностью противоречит нашим интуитивным представлениям. Но нужно помнить, что наша интуиция основана на опыте поведения обычных предметов соизмеримых с нами масштабов, а квантовая механика описывает вещи, которые происходят на микроскопическом и невидимом для нас уровне, — ни один человек никогда напрямую с ними не сталкивался. Если забыть об этом, мы неизбежно придем в состояние полного замешательства и недоумения. Для себя я сформулировал следующий подход к квантово-механическим эффектам: как только «внутренний голос» начинает твердить «такого не может быть!», нужно спросить себя: «А почему бы и нет? Откуда мне знать, как всё на самом деле устроено внутри атома? Разве я сам туда заглядывал?» Настроив себя подобным образом, вам будет проще воспринять статьи этой книги, посвященные квантовой механике.
Принцип Гейзенберга вообще играет в квантовой механике ключевую роль хотя бы потому, что достаточно наглядно объясняет, как и почему микромир отличается от знакомого нам материального мира. Чтобы понять этот принцип, задумайтесь для начала о том, что значит «измерить» какую бы то ни было величину. Чтобы отыскать, например, эту книгу, вы, войдя в комнату, окидываете ее взглядом, пока он не остановится на ней. На языке физики это означает, что вы провели визуальное измерение (нашли взглядом книгу) и получили результат — зафиксировали ее пространственные координаты (определили местоположение книги в комнате). На самом деле процесс измерения происходит гораздо сложнее: источник света (Солнце или лампа, например) испускает лучи, которые, пройдя некий путь в пространстве, взаимодействуют с книгой, отражаются от ее поверхности, после чего часть из них доходит до ваших глаз, проходя через хрусталик, фокусируется, попадает на сетчатку — и вы видите образ книги и определяете ее положение в пространстве. Ключ к измерению здесь — взаимодействие между светом и книгой. Так и при любом измерении, представьте себе, инструмент измерения (в данном случае, это свет) вступает во взаимодействие с объектом измерения (в данном случае, это книга).
В классической физике, построенной на ньютоновских принципах и применимой к объектам нашего обычного мира, мы привыкли игнорировать тот факт, что инструмент измерения, вступая во взаимодействие с объектом измерения, воздействует на него и изменяет его свойства, включая, собственно, измеряемые величины. Включая свет в комнате, чтобы найти книгу, вы даже не задумываетесь о том, что под воздействием возникшего давления световых лучей книга может сдвинуться со своего места, и вы узнаете ее искаженные под влиянием включенного вами света пространственные координаты. Интуиция подсказывает нам (и, в данном случае, совершенно правильно), что акт измерения не влияет на измеряемые свойства объекта измерения. А теперь задумайтесь о процессах, происходящих на субатомном уровне. Допустим, мне нужно зафиксировать пространственное местонахождение электрона. Мне по-прежнему нужен измерительный инструмент, который вступит во взаимодействие с электроном и возвратит моим детекторам сигнал с информацией о его местопребывании. И тут же возникает сложность: иных инструментов взаимодействия с электроном для определения его положения в пространстве, кроме других элементарных частиц, у меня нет. И, если предположение о том, что свет, вступая во взаимодействие с книгой, на ее пространственных координатах не сказывается, относительно взаимодействия измеряемого электрона с другим электроном или фотонами такого сказать нельзя.
В начале 1920-х годов, когда произошел бурный всплеск творческой мысли, приведший к созданию квантовой механики, эту проблему первым осознал молодой немецкий физик-теоретик Вернер Гейзенберг. Начав со сложных математических формул, описывающих мир на субатомном уровне, он постепенно пришел к удивительной по простоте формуле, дающий общее описание эффекта воздействия инструментов измерения на измеряемые объекты микромира, о котором мы только что говорили. В результате им был сформулирован принцип неопределенности, названный теперь его именем:
математическое выражение которого называется соотношением неопределенностей Гейзенберга:
где Δx — неопределенность (погрешность измерения) пространственной координаты микрочастицы, Δv — неопределенность скорости частицы, m — масса частицы, а h — постоянная Планка, названная так в честь немецкого физика Макса Планка, еще одного из основоположников квантовой механики. Постоянная Планка равняется примерно 6,626 x Дж·с, то есть содержит 33 нуля до первой значимой цифры после запятой.
Термин «неопределенность пространственной координаты» как раз и означает, что мы не знаем точного местоположения частицы. Например, если вы используете глобальную систему рекогносцировки GPS, чтобы определить местоположение этой книги, система вычислит их с точностью до 2-3 метров. (GPS, Global Positioning System — навигационная система, в которой задействованы 24 искусственных спутника Земли. Если у вас, например, на автомобиле установлен приемник GPS, то, принимая сигналы от этих спутников и сопоставляя время их задержки, система определяет ваши географические координаты на Земле с точностью до угловой секунды.) Однако, с точки зрения измерения, проведенного инструментом GPS, книга может с некоторой вероятностью находиться где угодно в пределах указанных системой нескольких квадратных метров. В таком случае мы и говорим о неопределенности пространственных координат объекта (в данном примере, книги). Ситуацию можно улучшить, если взять вместо GPS рулетку — в этом случае мы сможем утверждать, что книга находится, например, в 4 м 11 см от одной стены и в 1м 44 см от другой. Но и здесь мы ограничены в точности измерения минимальным делением шкалы рулетки (пусть это будет даже миллиметр) и погрешностями измерения и самого прибора, — и в самом лучшем случае нам удастся определить пространственное положение объекта с точностью до минимального деления шкалы. Чем более точный прибор мы будем использовать, тем точнее будут полученные нами результаты, тем ниже будет погрешность измерения и тем меньше будет неопределенность. В принципе, в нашем обыденном мире свести неопределенность к нулю и определить точные координаты книги можно.
И тут мы подходим к самому принципиальному отличию микромира от нашего повседневного физического мира. В обычном мире, измеряя положение и скорость тела в пространстве, мы на него практически не воздействуем. Таким образом, в идеале мы можем одновременно измерить и скорость, и координаты объекта абсолютно точно (иными словами, с нулевой неопределенностью).
В мире квантовых явлений, однако, любое измерение воздействует на систему. Сам факт проведения нами измерения, например, местоположения частицы, приводит к изменению ее скорости, причем непредсказуемому (и наоборот). Вот почему в правой части соотношения Гейзенберга стоит не нулевая, а положительная величина. Чем меньше неопределенность в отношении одной переменной (например, Δx), тем более неопределенной становится другая переменная (Δv), поскольку произведение двух погрешностей в левой части соотношения не может быть меньше константы в правой его части. На самом деле, если нам удастся с нулевой погрешностью (абсолютно точно) определить одну из измеряемых величин, неопределенность другой величины будет равняться бесконечности, и о ней мы не будем знать вообще ничего. Иными словами, если бы нам удалось абсолютно точно установить координаты квантовой частицы, о ее скорости мы не имели бы ни малейшего представления; если бы нам удалось точно зафиксировать скорость частицы, мы бы понятия не имели, где она находится. На практике, конечно, физикам-экспериментаторам всегда приходится искать какой-то компромисс между двумя этими крайностями и подбирать методы измерения, позволяющие с разумной погрешностью судить и о скорости, и о пространственном положении частиц.
На самом деле, принцип неопределенности связывает не только пространственные координаты и скорость — на этом примере он просто проявляется нагляднее всего; в равной мере неопределенность связывает и другие пары взаимно увязанных характеристик микрочастиц. Путем аналогичных рассуждений мы приходим к выводу о невозможности безошибочно измерить энергию квантовой системы и определить момент времени, в который она обладает этой энергией. То есть, если мы проводим измерение состояния квантовой системы на предмет определения ее энергии, это измерение займет некоторый отрезок времени — назовем его Δt. За этот промежуток времени энергия системы случайным образом меняется — происходят ее флуктуация, — и выявить ее мы не можем. Обозначим погрешность измерения энергии Δ Е. Путем рассуждений, аналогичных вышеприведенным, мы придем к аналогичному соотношению для Δ Е и неопределенности времени, которым квантовая частица этой энергией обладала:
Относительно принципа неопределенности нужно сделать еще два важных замечания:
он не подразумевает, что какую-либо одну из двух характеристик частицы — пространственное местоположение или скорость — нельзя измерить сколь угодно точно;
принцип неопределенности действует объективно и не зависит от присутствия разумного субъекта, проводящего измерения.
Иногда вам могут встретиться утверждения, будто принцип неопределенности подразумевает, что у квантовых частиц отсутствуют определенные пространственные координаты и скорости, или что эти величины абсолютно непознаваемы. Не верьте: как мы только что видели, принцип неопределенности не мешает нам с любой желаемой точностью измерить каждую из этих величин. Он утверждает лишь, что мы не в состоянии достоверно узнать и то, и другое одновременно. И, как и во многом другом, мы вынуждены идти на компромисс. Опять же, писатели-антропософы из числа сторонников концепции «Новой эры» иногда утверждают, что, якобы, поскольку измерения подразумевают присутствие разумного наблюдателя, то, значит, на некоем фундаментальном уровне человеческое сознание связано с Вселенским разумом, и именно эта связь обусловливает принцип неопределенности. Повторим по этому поводу еще раз: ключевым в соотношении Гейзенберга является взаимодействие между частицей-объектом измерения и инструментом измерения, влияющим на его результаты. А тот факт, что при этом присутствует разумный наблюдатель в лице ученого, отношения к делу не имеет; инструмент измерения в любом случае влияет на его результаты, присутствует при этом разумное существо или нет.