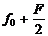Что такое широкополосный сигнал

Широкополосные сигналы

Смотреть что такое «Широкополосные сигналы» в других словарях:

ГОСТ Р ИСО 12124-2009: Акустика. Методы измерения акустических характеристик слуховых аппаратов на ухе человека — Терминология ГОСТ Р ИСО 12124 2009: Акустика. Методы измерения акустических характеристик слуховых аппаратов на ухе человека оригинал документа: 3.18 азимут на источник звука (azimuth angle of sound incidence): Угол между плоскостью симметрии… … Словарь-справочник терминов нормативно-технической документации

Многолучевой эффект — Многолучевой эффект это эффект, наблюдаемый при распространении сигналов. Возникает при условии существования в точке приема радиосигнала не только прямого, но и ещё одного или целого ряда отраженных лучей. Если говорить проще, на антенну… … Википедия

Радиолокация — (от Радио. и лат. locatio размещение, расположение) область науки и техники, предметом которой является наблюдение радиотехническими методами (радиолокационное наблюдение) различных объектов (целей) их обнаружение, распознавание,… … Большая советская энциклопедия

Сигнал (значения) — Сигнал изменение физической величины, несущее информацию, кодированную определённым способом, либо синхронизированное (заранее оговоренное с получателем) отсутствие изменения физической величины. Одно из фундаментальных понятий кибернетики. В… … Википедия

L-диапазон — Частотный спектр 1 2 ГГц Спектр длин волн от 30 до 15 см Классификация ITU (рус.) КНЧ СНЧ ИНЧ ОНЧ НЧ СЧ ВЧ ОВЧ … Википедия

ГИДРОАКУСТИЧЕСКАЯ СВЯЗЬ — обмен информацией через водную среду, по которой распространяются гидроакустические сигналы между надводными судами, подводными лодками, водолазами и т. д. Передаваемая информация речевые сигналы и кодированные сообщения. Гидроакустическая Связь… … Морской энциклопедический справочник

Стеганография — Не следует путать с стенографией. Запрос «Тайнопись» перенаправляется сюда; о тайнописи в Древней Руси см. Древнерусские тайнописи. Стеганография (от греч. στεγανός скрытый + γράφω пишу; буквально «тайнопись») это наука о… … Википедия

дифференциальное сравнение — 3.27 дифференциальное сравнение (differential comparison): Измерение, в котором уровень испытательного сигнала вычитается из УЗД в точке измерения. Примечание Если используются широкополосные сигналы, то должны быть измерены уровни звукового… … Словарь-справочник терминов нормативно-технической документации

коэффициент передачи звука открытого уха — 3.29 коэффициент передачи звука открытого уха (real ear unaided gain REUG): Разность между уровнем звукового давления в точке измерения и уровнем испытательного сигнала в зависимости от частоты испытательного сигнала при открытом ушном канале.… … Словарь-справочник терминов нормативно-технической документации

коэффициент передачи звука уха, закрытого включенным слуховым аппаратом — 3.33 коэффициент передачи звука уха, закрытого включенным слуховым аппаратом (real ear aided gain REAG): Разность между уровнем звукового давления в точке измерения и уровнем испытательного сигнала в зависимости от частоты испытательного сигнала… … Словарь-справочник терминов нормативно-технической документации

Источник

Теория радиоволн: аналоговая модуляция

Амплитудная модуляция

При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.

Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.

Данный спектр свойственен для модулирующего колебания постоянной частоты.

На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции

Источник

Что такое широкополосный сигнал

Для пояснения дальнейшего изложения мы сделаем здесь техническое отступление об особенностях различных диапазонов частот и о связанных с ними принципах построения радиосетей.

Современные средства радиосвязи работают на частотах в сотни мегагерц, в тысячи мегагерц (т.е. гигагерцы) и даже в десятки гигагерц. Радиоспектр разделен на участки, отведенные самым различным применениям; радиосвязь только одно из них. Распределение спектра в международном масштабе регламентируется соответствующим международным комитетом, в который входит и Россия. В России оно регулируется межведомственным Государственным Комитетом по Радиочастотам (ГКРЧ). Мы вернемся к этому позднее.

Каждый участок радиоспектра нарезан на каналы одинаковой «ширины» (например, по 25 килогерц для сотовой телефонии). Максимальная скорость передачи данных в данном канале зависит только от ширины канала, а не от участка спектра, в котором он находится. Понятно, что в диапазоне частот, скажем, от 8 гигагерц до 9 гигагерц уложится в 10 раз больше каналов определенной ширины, чем в диапазоне от 800 мегагерц до 900 мегагерц. Таким образом, чем выше частоты, тем больше общая «емкость» диапазона в смысле возможности одновременных передач: если представить себе 800-мегагерцевый диапазон как тысячежильный кабель, то 8-гигагерцевый диапазон будет уже десятитысячежильным кабелем.

Можно было бы предположить, что колоссальная емкость сверхвысокочастотной (СВЧ) части радиоспектра может решить все проблемы радиосвязи. Это почти так, но есть одна чисто физическая особенность радиоволн: чем выше частота волны (т.е. чем короче ее длина), тем меньших размеров препятствия она способна огибать. Поэтому, скажем, мобильная сотовая связь может работать на частотах не выше 2 гигагерц: на более высоких частотах связь уже строго ограничена прямой видимостью (почти как для светового луча), так что связь с мобильным телефоном будет прерываться как свет от фонаря, когда идешь перед частоколом.

Замечание: Мобильная сотовая сеть строится по тому же принципу, но с использованием ненаправленных антенн также и у мобильных абонентов, которые не мешают при этом друг другу как потому, что говорят всегда на разных каналах (или чередуясь на одном и том же канале), так и потому, что сигнал от мобильного аппарата гораздо слабее сигнала от базовой станции и может быть правильно принят только базовой станцией, но не другим мобильным аппаратом.

Для того, чтобы послать радиосигнал большой мощности в СВЧ-диапазоне, нужен дорогостоящий передатчик с усилителем и дорогостоящая антенна большого диаметра. Для того, чтобы принять без помех сигнал малой мощности, также нужна дорогая большая антенна и дорогой приемник с усилителем.

Так обстоит дело при использовании обычного «узкополосного» радиосигнала, когда передача происходит на одной определенной частоте, а точнее, в узкой полосе радио-спектра, окружающей эту частоту (частотном канале). Картину усложняют еще и различные взаимные помехи между узкополосными сигналами большой мощности, передаваемыми близко друг от друга или на близких частотах. В частности, узкополосный сигнал может быть просто заглушен (случайно или намеренно) передатчиком достаточной мощности, настроившимся на ту же частоту.

Суммируя, мы можем выделить следующие свойства ШПС-технологии, по крайней мере для метода прямой последовательности:

— Не создаются помехи другим устройствам.

— Экономичность при массовом производстве.

— Возможность повторного использования одного и того же участка спектра.

Другая пара передатчик-приемник будет использовать и другую последовательность переключений частот, заданную независимо от первой. В одной полосе частот и на одной территории прямой видимости (в одной «ячейке») таких последовательностей может быть много. Ясно, что при возрастании числа одновременных передач возрастает и вероятность коллизий, когда, например, два передатчика одновременно перескочили на частоту №45, каждый в соответствии со своей последовательностью, и заглушили друг друга.

Метод частотных скачков, так же как и описанный выше метод прямой последовательности, обеспечивает конфиденциальность и некоторую помехозащищенность передач. Помехозащищенность обеспечивается тем, что если на каком-нибудь из 79 подканалов передаваемый пакет не смог быть принят, то приемник сообщает об этом, и передача этого пакета повторяется на одном из следующих (в последовательности скачков) подканалов.

С другой стороны, поскольку при использовании метода частотных скачков, в отличие от метода прямой последовательности, на каждом подканале передача ведется на достаточно большой мощности (сравнимой с мощностью обычных узкополосных передатчиков), про этот метод нельзя сказать, что он не мешает другим видам передач.

Другие новости Wireless:

25 декабря 2019 года компания CompTek приглашает принять участие в техническом воркшопе на тему «Планирование сети Wi-Fi: коротко о сложном».

Материал подготовлен при поддержке компании Ruckus Networks 802. 11ax – это новый стандарт WiFi, позволяющий решить многие проблемы предприятий.

Источник

ШИРОКОПОЛОСНЫЕ СИГНАЛЫ, СВОЙСТВА, ТИПЫ,

В. Ф. Попов

«МЕТОДЫ И УСТРОЙСТВА ФОРМИРОВАНИЯ И ОБРАБОТКИ ШИРОКОПОЛОСНЫХ СИГНАЛОВ»

В.И.Сединин, д-р техн. наук, проф., зав. кафедрой «САПР»

Сибирского государственного университета телекоммуникаций и информатики;

В.А. Алгазин, к. ф.- м. наук, доцент, зам. Директора ОФИМ СОРАН по информатизации

В учебном пособии излагаются основные теоретические положения формирования, оценки качества и обработки ФМ и частотно-дискретных широкополосных сигналов (ШПС) на основе линейных и нелинейных псевдослучайных последовательностей (ПСП). Эти положения необходимы для решения задач синтеза и анализа современных и перспективных помехозащищенных широкополосных систем радиолокации или связи с кодовым разделением абонентов и большим объемом ансамбля ШПС, которые реализуются методами прямого расширения спектра сигнала, псевдослучайной перестройки рабочей частоты (ППРЧ).

Пособие содержит примеры решения задач и перечень задач для самостоятельной работы студентов.

Пособие предназначено для студентов дневной и заочной форм обучения специальности 210402 «Средства связи с подвижными объектами» и 210302 «Радиотехника», магистров направлений «Инфокоммуникационные технологии и системы связи», «Телекоммуникация» и «Радиотехника», а также может быть полезным радиоинженерам и студентам других специальностей.

Печатается по решению редакционно-издательского совета

Омского государственного технического университета

УДК 621.396(075)

ББК 32.811я73

ISBN978-5-8149-0817-9 ГОУ ВПО «Омский государственный

Технический университет», 2011

Введение

Решение задач статистического синтеза и анализа устройств формирования, приема и обработки широкополосных шумоподобных сигналов (ШПС) широкополосных систем связи (ШСС) и радиолокации требует от студентов достаточно высокой математической подготовки и встречает определенные затруднения.

Целью издания учебного пособия является ознакомление студентов с современными достижениями отечественных и зарубежных ученых по синтезу ШПС и систем ШПС на основе линейных и нелинейных псевдослучайных последовательностей (ПСП) и выработка у студентов навыков по синтезу и анализу качества ШПС, ШСС в целом и ее элементов.

В пособии изложены основные свойства, типы ШПС, методы построения ШСС, свойства и методы формирования и обработки линейных и нелинейных фазоманипулированных (ФМ) ШПС, дискретно частотных сигналов (ДЧС). Кроме того дана оценка помехоустойчивости асинхронно-адресной ШСС с кодовым разделением абонентов при различных видах помех, рассмотрены методы реализации поиска и синхронизации ШПС и приведены оценки временных затрат поиска и синхронизации.

В приложении приведены примеры синтеза согласованных фильтров (СФ) ШПС, а также периодически повторяющихся сигналов с накоплением в рециркуляторе. Даны теоретические сведения, рекомендации для решения задач и перечень задач, которые предназначены для домашних заданий, а также для использования при выполнении курсовых работ и проектов по следующим разделам курса:

1. Синтез производных систем ФМ, ДЧ ШПС с большим ансамблем сигналов.

2. ШСС с прямым расширением спектра, псевдослучайной перестройкой частоты (ППРЧ) и помехоустойчивым кодированием.

При подготовке пособия использованы материалы монографий, книг известных ученых в области теории связи и радиолокации: Л.Е. Варакина, Дж. Прокиса и др., а также материалы статей Ю.В. Гуляева, В.Я. Кислова и др., опубликованных в периодической литературе по данной тематике, в том числе и работы автора учебного пособия.

ШИРОКОПОЛОСНЫЕ СИГНАЛЫ, СВОЙСТВА, ТИПЫ,

Свойства ШПС

Широкополосные сигналы позволяют:

— 1). Обеспечить высокую помехозащищенность ШСС, определяемую помехоустойчивостью, энергетической и структурной скрытностью ШПС. При корреляционном приеме ШПС или приеме на согласованный фильтр (СФ) увеличение выходного отношения сигнал/шум (ОСШ)

(1.3)

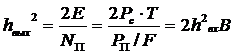
относительно входного h_вх 2 =Р_с/Р_П равно 2В.

При больших В можно обеспечить высокую помехоустойчивость при h_вх 2 > В число сигналов в системеравно:

, (1.5)

где с, n – const и n >1.

Кроме того смена ШПС из ансамбля L в сеансе связи обеспечивает структурную (параметрическую) скрытность ШСС.

Сигналы, входящие в систему, должны обеспечивать минимум взаимных помех, определяемый уровнем максимальных пиков взаимокорреляционной функции (ВКФ) R_ijсигналов i и j

, (1.6)

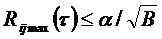
где α -пик-фактор ВКФ; чем меньше α, тем лучше ВКФ;

— 3). Бороться с многолучевостью сигнала разделением лучей. Минимальная задержка между разделяемыми лучами определена полосой F ШПС:

(1.7)

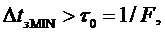
где τ₀ – ширина АКФ R(τ) ШПС;

— 4). Обеспечить совместимость передачи информации с измерением параметров расстояния и скорости движения объекта в системах подвижной связи. Среднеквадратическая погрешность измерения:

— расстояния (по задержке сигнала) равна

; (1.8)

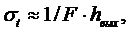
-скорости (по доплеровскому смещению частоты) равна

, (1.9)

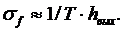
т.е. зависят от составляющих базы ШПС, изменяемых независимо;

— 5). Обеспечить электромагнитную совместимость ШСС с узкополосными системами связи (УПС). Помехоустойчивость ШПС при УПС помехи равна (1.3), где h_вх 2 =Р_ШПС/Р_У, а усиление обработки В.

Мощность ШПС помехи на выходе приемника УПС равна (Р_ШПС/F)·F_У ипомехоустойчивость УПС равна также (1.3), где h_вх 2 =Р_У/Р_ШПС и В=F/F_У.

1.2. Основные типы ШПС

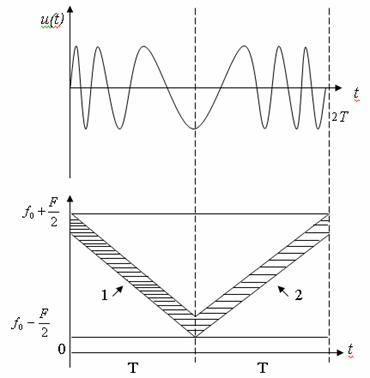
Частотно-модулированные (ЧМ) сигналы. Частота сигнала

меняется по заданному закону Рис.1.1.

Рис. 1.1. ЧМ сигнал с модуляцией по V – закону на интервале 2Т, состоящий из

двух сигналов с линейной ЧМ (ЛЧМ): 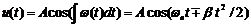, где

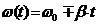
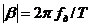
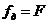
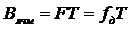
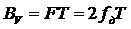
мгновенная частота , знак «-» для эпюры 1, а знак «+» для эпюры2; а -скорость изменения ЛЧМ; -девиация частоты.

, (1.10)

где 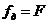— девиация частоты. Такие сигналы используются в радиолокации, связи с приемом СФ на ПАВ.

На частотно-временной плоскости Рис.1.2 штриховкой выделено распределение энергии одного элемента МЧ сигнала на частоте f_k. Все элементы полностью перекрывают квадрат со сторонами F и T. База сигнала B равна площади квадрата. Ширина спектра элемента .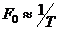

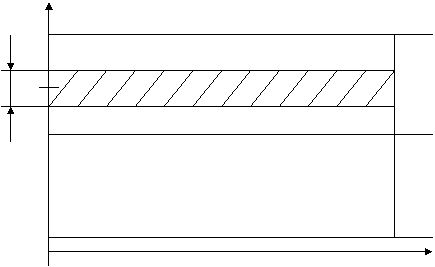
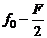
f

Т

Рис. 1.2. МЧ сигнал на частотно-временной плоскости.

Поэтому база МЧ сигнала:

(1.11)

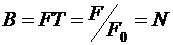
совпадает с числом гармонических сигналов и для большой базы B требуется большое число частотных каналов N. Однако, для уменьшения влияния многолучевости весьма эффективны сигналы ОFDM с Т>> 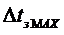, занимающие по величине B промежуточное положение между ШПС и УПС. Недостатком МЧ сигналов является большой пик – фактор.

Фазоманипулированные (ФМ) сигналы представляют последовательность радиоимпульсов, фазы которых изменяются по заданному закону (рис.1.3а)

Рис.1.3. Фазоманипулированные (ФМ) сигналы.

Модулированный по амплитуде и фазе радиосигнал можно записать в общем виде

(1.12)

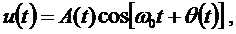
где медленно меняющиеся по закону модулирующего сигнала:

— A(t) огибающая АМ сигнала (рис.10.3.б)

, (1.13)

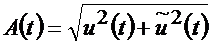
где 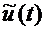— преобразование Гильбертаот u(t);

— Ө(t) фаза ФМ сигнала рис.1.3.в ( принимает обычно значения 0 или ).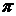

Сигнал (1.12) является реальной частью комплексного сигнала

(1.14)

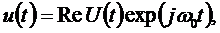
где комплексная огибающая сигнала равна

(1.15)

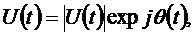
а модуль — огибающая (1.13) сигнала u(t).

Таким образом, ФМ радиочастотному сигналу (1.12) соответствует видео ФМ сигнал U(t), состоящий из положительных и отрицательных импульсов (рис.1.4) с симметричным спектром относительно .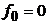

F≈2/

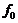
=0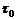

0 t

Рис. 1.4. Фазоманипулированный видеосигнал и ЧВП.

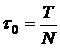
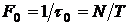
Если число импульсов N, то длительность одного импульса , а ширина его спектра равна приближенно ширине спектра сигнала . На частотно-временной плоскости (ЧВП) штриховкой выделено распределение энергии одного элемента (импульса) ФМ сигнала.

Все элементы перекрывают выделенный квадрат со сторонами F и T. База сигнала равна:

, (1.16)

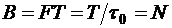
т. е. числу импульсов в сигнале.

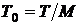
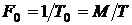
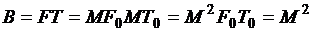
Дискретные частотные сигналы (ДЧС)представляют последовательность радиоимпульсов, несущие частоты которых изменяются по заданному закону. Если число импульсов в ДЧ сигнале равно M, то длительность импульса , а ширина его спектра . Энергия этих сигналов распределена не равномерно на ЧВП. База ДЧ сигналов

, (1.17)

т.к. база импульса .

Достоинство ДЧ сигналов перед МЧ сигналами состоит в том, что для получения необходимой базы значение 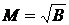значительно меньше. Однако, более эффективны ДСЧ сигналы.

Дискретные составные частотные сигналы (ДСЧ) являются ДЧ сигналами, у которых каждый импульс заменен псевдослучайным ШПС. На рис. 1.5а изображен видео ФМ сигнал, отдельные части которого передаются на различных несущих частотах. На рис. 1.5б штриховкой выделено распределение энергии ДСЧ сигнала.

U(t)

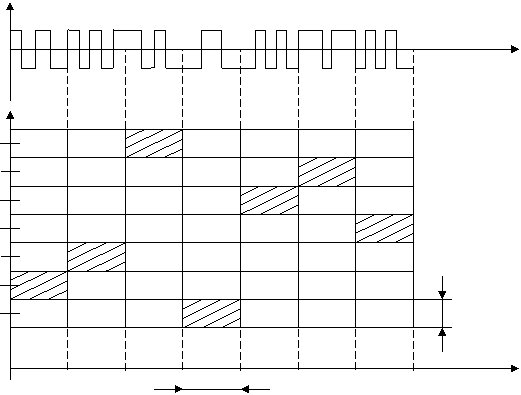
Рис. 1.5. ДСЧ-ФМ сигнал. (Составной сигнал с кодовой ЧМ и ФМ (СКЧМ-ФМ)).

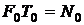
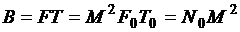
Площадь — равна числу импульсов ФМ сигнала в одном частотном элементе ДСЧ сигнала. База ДСЧ сигнала

. (1.18)

При этом число импульсов полного (на интервале Т) ФМ сигнала равно

.

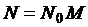
Такой сигнал называют ДСЧ-ФМ сигналом. Известны ДСЧ-ЧМ сигналы на основе кодовой ЧМ и частотной манипуляции (ДЧС вместо ФМ ШПС).

Методы построения ШСС.

ШПС являются псевдослучайными сигналами со свойствами случайного шума и могут формироваться по детерминированным законам.

(1.19)

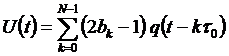
В ШСС с ШПС ширина спектра огибающей модулированного радиосигнала не определяется (в отличие от УПС) скоростью передачи информации, а определяется шириной спектра ПСП.

Прямое расширение спектра (ПРС) в ШСС с ФМ-2 реализуют модуляцией информационного сигнала U_инф.(t) БВНс амплитудами ±1 сигналом БВН U(t) ПСП (1.19), т.е. перемножением. Сигнал БВН этого произведения U_прс(t)=U_инф.(t)U(t) с амплитудами ±1 является модулирующим сигналом ФМ-2 ШПС с ПРС и является огибающей радиосигнала ФМ-2 ШПС с ПРС, который можно записать в виде:

. (1.20)

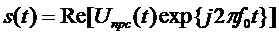
Структурная схема ШСС ФМ-2 ШПС с ПРС дана на рис.1.6.

Рис. 1.6. ШСС с ПРС ФМ-2 ШПС (база В = ): С- синхронизатор,

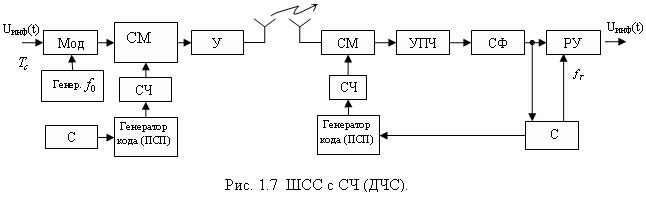
При расширении спектра радиосигнала скачками по частоте (СЧ) частота несущего колебания изменяется дискретно во времени (ДЧС), принимая конечное число разных значений. Последовательность её значений можно рассматривать как ПСП, которая формируется в соответствии с некоторым кодом. Структурная схема ШСС с СЧ представлена на рис.1.7, а база ДЧС сигнала определена выражением (1.17).

ШСС с ДСЧ-ФМ сигналом (рис. 1.5) можно построить комбинацией формирователей ФМ ШПС (рис. 1.6.) и ДЧС ШПС (рис.1.7.): первоначально формируется ФМ-2 ШПС, а затем ДЧС ШПС. Другие варианты реализации ШСС с ПРС и СЧ рассмотрены в работах [2, 19].

Сигналы

Максимальные уровни боковых пиков апериодических АКФ ПСП конечной длительности можно уменьшить, применяя многофазные сигналы и амплитудно-фазоманипулированные сигналы.

Многофазные сигналы можно построить дискретизацией аналоговых сигналов с ЧМ, например, линейно-частотной модуляцией (ЛЧМ). На рис.2.8, изображена зависимость фазы θ от t огибающей сигнала с ЛЧМ (рис.1.1) в форме записи (1.15).

Рис.2.8. Зависимость фазы θ огибающей сигнала с ЛЧМ

, где .

ЛЧМ сигнал длительностью Т можно представить в виде последовательности N радиоимпульсов с мгновенной частотой, линейно изменяющейся в течение импульса Значения линейно-ломанной аппроксимирующей дискретной функции совпадают с непрерывной θ(t) в точках, кратных τ₀, т.е. θ_n=θ (n τ₀), n = 0,1,…N-1.

Если в качестве начальных фаз многофазного сигнала ЧМ взять

θ_фn=(θ_n+θ_n+1)/2, то начальные фазы n-го импульса многофазного сигнала, соответствующего аналоговому сигналу ЛЧМ, равны:

Меняя β (т.е. θ_фn ) получим систему многофазных сигналов.

Модуль АКФ такого многофазного сигнала равен

. (2.42)

В качестве аналогового сигнала можно взять также сигнал с квадратичной частотой модуляцией (КЧМ). Известно, что модули АКФ этих аналоговых и соответствующих многофазных сигналов близки, а боковые пики

Если произвести двоичное квантование (клипирование) по уровню АФМ сигнала (рис.2.9а), т.е. получить (рис.2.9б), то получим ФМ сигнал, АКФ которого будет обладать большими, но все же достаточно малыми боковыми пиками.

Рис.2.9. АФМ сигнал (а), ФМ сигнал (б), АКФ ФМ сигнала (в).

Например, АФМ сигнал с квадратичным фазовым спектром при N=37 имеет максимальный боковой пик АКФ 1,5%. При этом максимальный боковой пик АКФ ФМ сигнала (рис.2.9в) равен 5/37=0.135, что несколько меньше Можно показать, что среднеквадратичное значение боковых пиков АКФ таких ФМ сигналов (при оптимальном выборе их параметров) равно т.е. такие сигналы можно отнести к оптимальным (или минимаксным) ФМ сигналам.

Минимаксными ФМ сигналами называют сигналы, у которых максимальные боковые пики АКФ минимальны.

2.4.3.Cистемы ФМ сигналов

Ранее отмечалось, что для помехозащищенных ШСС требуется большой объем L (1.5) нормальных и больших систем ФМ ШПС.

К такому объему можно приблизиться, реализуя системы сигналов на основе, например, систем Уолша или производные системы [1] ФМ сигналов на основе М-последовательностей.

Система сигналов Уолша. Многие системы ФМ сигналов образованы на базе систем сигналов Уолша, построенных на основе матрицы Адамара

, (2.43)

Полагая H₁=1 из (2.43) можно получить матрицы порядка 2

(2.43′)

В качестве КП системы Уолша можно брать строки или столбцы матрицы Адамара. Число этих КП (объём системы) равно порядку матрицы N.

. (2.44)

На рис.2.10 приведены ПСП системы Уолша согласно матрице Н₈, которые упорядочены по числу блоков μ в последовательности.

Рис.2.10. Система сигналов Уолша.

Отметим, что число блоков μ в различных последовательностях изменяется от 1 до N, и плохо согласуется с блоковой структурой кода СП (2.23), (2.27). Поэтому система сигналов Уолша обладает плохими корреляционными свойствами, т.е. АКФ и ВКФ имеют большие боковые пики.

На базе систем Уолша можно строить производные системы сигналов.

Производным сигналом называют сигнал, образованный посимвольным произведением двух или более исходного и производящего сигналов, которые могут быть узкополосными и широкополосными.

К таким системам можно отнести:

—сегментные cистемы, реализуемые путем выделения перекрывающихся или не перекрывающихся сегментов (отрезков) из ПСП на основе М-последовательности большой длины N;

—циклические системы Голда, Касами.

Выбор производящего сигнала зависит от исходного сигнала. Если исходный сигнал U широкополосный, то производящий V тоже широкополосный с малыми уровнями боковых пиков ФН. Если исходный сигнал узкополосный, то для производящего сигнала достаточно многократное превышение полосы исходного сигнала и малый уровень боковых пиков АКФ.

Производные сегментные системы сигналов. Обозначим комплексную огибающую (1.15) исходной М-последовательности U(t), где

0 ≤ t ≤T, а модуль огибающей (1.13) производящего сигнала V(t)=1, 0 ≤ t ≤ T₀, гдеT₀ 2, то будем называть сигнал многофазным. Этим ПСП можно поставить в однозначное соответствие цифровые кодовые ПСП <а(ν)>, ,символы которых а(ν), b(ν) принадлежат аддитивным р-ичным группам.

Формирование КФ (2.18) сводится к перемножению символов А(ν) и В*(ν) с последующим суммированием, где *-знак комплексной сопряженности.

При переходе к символам а(ν), b(ν) КФ определяется через разности этих символов по mod p на основе сравнения (Примечание стр.23)

, т.е. . (2.47)

Для циклических систем ФМ сигналов ПСП <а(ν)>, должны обладать следующим циклическим свойством: разность по mod p ПСП и её циклической перестановкой является другой циклической перестановкой исходной ПСП, т.е.

где λ≠0 и λ≠μ(mod p). Аналогично:

Равенства (2.48) выполняются для М-последовательностей согласно их аддитивно-циклическим свойствам.

Пример. Циклические перестановки получаются так: исходная ПСП записывается в виде периодической бесконечной ПСП:

Циклическая система сигналов состоит из последовательностей <С_j(ν)>, символы которых определяются равенством

где

Каждая ПСП циклической системы равна разности между ПСП и ПСП циклической перестановки , т.е.

Такие циклические системы являются производными, где система последовательностей является исходной, а ПСП

Известно, что ВКФ сигналов циклической системы определяются периодическими ВКФ, ВФН образующих последовательностей. Поэтому для построения циклической системы минимаксных сигналов (R_max→min) необходимо, чтобы периодические ВКФ и ВФН образующих сигналов имели малые боковые пики (R_max(λ)→min). Общего метода построений таких сигналов нет.

Примитивным называют неприводимый (не может быть представлен в виде произведения) многочлен, одним из корней которого является примитивный элемент поля Галуа GF(2 n ).

Такие образующие ПСП выбираются по известным [1] таблицам неприводимых многочленов и периодические нормированные ВКФ ПСП циклической системы сигналов являются случайными уровнями с

максимальными боковыми пиками

R_max (λ ) ≤ 1,4/ , (2.51)

что меньше в 2 раза, чем для полного кода (3/ ).

Из этой пары ПСП ν)> и ν)> образуем согласно (2.50) ансамбль

Если включить в этот ансамбль и исходные ПСП ν)> и ν)>, то получим ансамбль из (N+2)=33 ПСП. Эти ПСП называют последовательностями Голда, из которых 31 ПСП не являются последовательностями максимальной длины. Схема реализации генератора предпочтительных М-последовательностей, которым соответствуют примитивные многочлены (2.50′), и генератора ПСП Голда представлена на рис.2.10′.

Рис.2.10′. Схема реализации генератора предпочтительных

М-последовательностей (2.50′) и соответсвующих ПСП Голда

АКФ ансамбля из 31 ПСП Голда не являются в отличие от М-последо-вательностей двоичными. Голд показал, что значения ВКФ любой пары ПСП ансамбля (N+2) последовательностей Голда и пиковые значения не нормированной АКФ R_max являются троичными с возможными значениями <-1,-t(k), t_k-2>, где уровень t(k) определен (2.32′).

Циклические последовательности Касами образуются аналогичными процедурами согласно (2.50), где, если ввести задержку D(j), то можно записать в виде:

j(ν)>= <А(ν)> , (2.52)

где символ — посимвольное умножение последовательностей и , а произведение D(j)B(ν) является символом B(ν), сдвинутым на jтактов. Число всех ПСП равно N+2 (N сдвигов плюс две исходных ПСП).

Для малой системы Касами с ансамблем

ij(ν)>= <А(ν)> , (2.53)

При значении степени характеристического полинома исходных ПСП 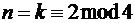объем большой системы Кассами: ,

а при соответственно

При больших п объем боль

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Источник