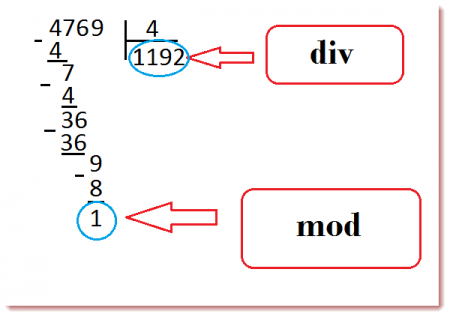
Что такое целочислительное деление
Что такое целочислительное деление
Оператор div и оператор mod
В этой статье речь пойдет о целочисленном делении и делении с остатком.
То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.
Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e
Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так
z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!
А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.
Например (40 / 6) с остатком = 4 с оператором mod будет такой
Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.
Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим
Целочисленная арифметика. Делим с округлением результата. Часть 1
Чем проще, на первый взгляд, задача, тем меньше разработчик вдумывается в то, как грамотно её реализовать, и допущенную ошибку, в лучшем случае, обнаруживает поздно, в худшем — не замечает вовсе. Речь пойдет об одной из таких задач, а именно, о дробном делении и о масштабировании в контроллерах, поддерживающих исключительно целочисленную арифметику.
Почему тонкостям вычислений в условиях такой арифметики разработчики прикладных программ не уделяют внимание, вопрос. Рискну только предположить, что, по всей вероятности, сказывается привычка производить вычисления на калькуляторе… Во всяком случае, с завидной регулярностью «имею счастье» лицезреть, как коллеги по цеху наступают на одни и те же грабли. Этот материал нацелен на то, чтобы те самые «грабли» нейтрализовать.
При целочисленной арифметике результат деления одного целого числа на другое состоит из двух чисел — частного и остатка. Если остаток деления отбросить, получим результат, в абсолютной величине округленный до меньшего целого.
Реализуя вычисления с дробями, этот момент частенько упускают из вида, а, упустив, получают потери в точности вычислений. Причем точность вычислений падает с ростом величины делителя. К примеру, что 53/13, что 64/13 дадут в результате 4, хотя, по факту, частное от деления второй дроби существенно ближе к 5.
На самом деле, округление результата до ближайшего целого организовать элементарно. Для этого достаточно удвоить остаток деления, просуммировав его сам с собою, а затем вновь поделить его на то же число, на которое делили первоначально, и частное от этого деления сложить с частным, полученным от первоначальной операции деления.
Принимая во внимание то, что такие вычисления в программе могут потребоваться неоднократно, алгоритм вычислений реализуем в формате, пригодном для упаковки в подпрограмму.
Для корректного выполнения необходимых для этого промежуточных вычислений понадобится массив из пяти регистров, обозначим его условно TEMP[0..4]. Почему пять и не меньше, поясню чуть ниже.
Шаги с 3-го по 7-й могут быть вынесены в подпрограмму.
При желании, запись результата может быть произведена непосредственно суммированием TEMP[0] c TEMP[1] за пределами подпрограммы расчета. Это непринципиально. Единственное, следует иметь в виду, что при множестве однотипных расчетов вынос операции сложения в основное тело программы способен привести к возрастанию задействованного ею объема программной памяти.
Так почему же для промежуточных вычислений потребовалось целых 5 регистров? А операция суммирования остатка деления самого с собой, о чем говорилось ранее, заменена умножением остатка на два? Очень просто — для того, чтобы оперировать с неограниченным набором целых чисел.
То бишь, удвоенный остаток от целочисленного деления дроби в интересах округления результата такого деления всегда должен быть представлен в формате double integer.
Целочисленное деление и деление по модулю
Целочисленное деление несколько отличается от обычного. Целочисленное деление — это то же caмoe деление, которое вы изучали, когда ходили в первый класс. При делении числа 21 на число 4 (21/4) в случае целочисленного деления в ответе получается 5 и остаток 1.
Чтобы получить остаток, нужно число 21 разделить по модулю 4 (21 % 4), в результате получим остаток 1.
Операция деления по модулю иногда оказывается весьма полезной, например, если вы захотите вывести из ряда чисел каждое десятое значение. Любое число, результат деления которого по модулю 10 равен нулю, является кратным десяти, т.е. делится на 10 без остатка. Так, результат выражения 1 % 10 равен 1; 2 % 10 равен 2 и т.д.; а 10 % 10 равен 0. Результат от деления 11 % 10 снова равен 1; 12 % 10 снова равен 2; и так можно продолжать до следующего числа, кратного 10, которым окажется 20. Мы воспользуемся этим методом при рассмотрении циклов на занятии 7.
При делении 5 на 3 я получаю в ответе 1. В чем моя ошибка?
При делении одного целого числа на другое в качестве результата вы также получите целое число. Следовательно, 5/3 равно 1.
Для получения дробного результата нужно использовать вещественные числа. Выражение 5,0 / 3,0 даст дробный ответ: 1,66667.
Если ваш метод принимает в качестве параметров целочисленные значения, нужно привести их к типу float.
Вопросы и ответы: Выполняя операцию приведения типа переменной, вы заставляете компилятор изменить ее тип. Приэтом вы как будто говорите своемукомпилятору:»Я знаю, что делаю». Было бы неплохо, если бы это оказалось правдой, поскольку компилятор как бы отвечает вам: «Как скажете, босс: вся ответственность ложится на вас». В данном случае мы хотим сказать компилятору: «Я понимаю, что ты считаешь это значение целым, но я знаю, что делаю: это действительно вещественное значение». Для приведения типа существует два способа. Можно использовать приведение типа в старом стиле С или новый улучшенный оператор ANSIstatic_cast. Оба варианта демонстрируются в листинге 4.3.
Листинг 4.3. Приведение переменной к типу float
3: void intDiv(int x, int y)
6: cout (y); // современный стиль
7: int myAge = 39; // инициализируем две целочисленные переменные
9: cout yourAge; // значение переменной myAge больше значения переменной yourAge? также возвратит 0 (или false).
Предупреждение: Многие начинающие программировать на языке C++ путают оператор присваивания (=) с оператором равенства (==). Случайное использование не того оператора может привести к такой ошибке, которую трудно обнаружить.
Всего в языке C++ используется шесть операторов отношений: равно (==), меньше ( ), меньше или равно ( =) и не равно (!=). В табл. 4.1 не только перечислены все операторы отношений, но и приведены примеры их использования.
Рекомендуется:Помните, что операторы отношений true или false.
He рекомендуется: Не путайте оператор присваивания (=) с оператором равенства (==). Это одна из самых распространенных ошибок программирования на языке C++ — будьте начеку!
Ошибка! Недопустимый объект гиперссылки.
Оператор if
Обычно программа выполняется по порядку, строка за строкой. Оператор if позволяет проверить условие (например, равны ли две переменные) и изменить ход выполнения программы, направив ее в другое русло, которое будет зависеть от результата сравнения. Простейшая форма оператора if имеет следующий вид:
Условие в круглых скобках может быть любым выражением, но обычно оно содержит операторы отношений. Если это выражение возвращает false, то последующий оператор пропускается. Если же оно возвращает значение true, то оператор выполняется. Рассмотрим следующий пример:
Здесь сравниваются значения переменных bigNumber и smallNumber. Если значение переменной bigNumber больше, то во второй строке этого программного фрагмента ее значение устанавливается равным значению переменной smallNumber.
Поскольку блок выражений, заключенных в фигурные скобки, эквивалентен одному выражению, то это свойство позволяет за строкой с оператором if использовать целые блоки, которые могут быть довольно обширными:
Вот простой пример применения блока выражений:
Деление в Python
Python — популярный высокоуровневый язык программирования. Он обладает большим набором инструментов, имеет динамическую типизацию и используется для решения любых видов задач.
Деление в Python разделяется на три вида: обычное, целочисленное и взятие остатка. Программисту не нужно заботиться о типах операндов, Python сам определяет их и приводит результат к нужному виду. Как это делается, разберемся в этой статье.
Оператор деления
Деление в Python обозначается косой чертой «/». Примечательно, что результат в консоле всегда приводится к типу «float», даже если оба операнда были целочисленного типа, об этом свидетельствует появление «.0» у полученного значения.
Это появилось в 3-ей версии Python, ранее результатом деления целых чисел было только целое число, чтобы получить дробный результат, программисты явно указывали одному из операндов тип «float», в противном случае дробная часть просто отбрасывалась.
Важно понимать, что деление в Python, как и другие операции, работает медленнее, чем в более низкоуровневых языках программирования. Это связано с высоким уровнем автоматизации и абстракции, из-за динамической типизации интерпретатор вынужден приводить числа к дробному типу «float», который требует большего количества памяти.
Деление в представлении человека отличается от его представления в компьютере. Компьютер устроен так, что все арифметические операции могут выполняться только через сложение. Это значит, что быстрее всего выполняется сложение, затем вычитание, где необходимо менять знак операндов, умножение, где число складывается много раз. Деление выполняется дольше всех, потому что помимо многократно повторяющейся операции сложения необходимо также менять знак операндов, что требует больше памяти и действий.
Из примера видно, что не смотря на то, что во всех случаях операция была между целыми числами, результатом деления в Python 3 является вещественное число. В первом случае мы даже специально использовали приведение к типу int.
Деление без остатка
Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».
В отличие от других языков программирования Python позволяет результату целочисленного деления быть как целым (int), так и дробным (float) числом. В обоих случаях дробная часть отбрасывается и получается число с окончанием «.0».
Примеры нахождения целой части от деления:
В первых двух случаях деление осуществлялось между целыми числами. Поэтому в результате было получено целое число. В третьем примере одно из чисел вещественное. В этом случае в результате получаем так же вещественное число (типа float), после запятой у которого 0.
Остаток
Для получения остатка от деления в Python 3 используется операция, обозначающаяся символом процента «%». Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.
Определение остатка от деления очень часто используется в программах для нахождения, допустим, чётных чисел. Или, например, если обработка данных выполняется в цикле, и нужно выводить в консоль сообщение о ходе обработки не каждый раз, а на каждой 10-ой итерации.
Вот пример вывода чётных чисел из списка в консоль:
Проблемы чисел с плавающей точкой
Компьютер устроен так, что на аппаратном уровне понимает только две цифры: один и ноль. Из-за этого при делении и других операциях с дробями часто возникают проблемы. Например, 1/10 в двоичном представлении является неправильной бесконечной дробью. Её нельзя написать полностью, поэтому приходится округлять, а выбор значения при округлении ограничен нулем и единицей.
Что говорить о делении, если ошибки возникают и при операции сложения. Если сложить число «0.1» с самим собой четырнадцать раз, то получиться 1.400…01. Откуда взялась эта единица? Она появилась при переводе числа из двоичного вида в десятичный.
Более технически сложное деление приводит к подобным неточностям гораздо чаще. Обычно Python округляет результат так, что пользователь не замечает этой проблемы, но если получается достаточно длинное число, то проблема проявляется.
Деление комплексных чисел
Комплексные числа — это числа вида «a + b·i». Они занимают наивысшую ступень в иерархии чисел, арифметические операции над ними существенно отличаются от операций над обычными числами.
Деление комплексного числа на обычное меняет лишь длину радиус вектора, но не его направление.
Сокращенные операции деления
Чтобы упростить жизнь программистов, разработчики Python включили в язык «сокращенные операции». Их используют если надо выполнить операцию над переменной и полученный результат записать в эту же переменную. То, что записывается в длинной форме, можно записать в более короткой по следующим правилам:
| Полная форма | Краткая форма | |
| Деление | a = a / b | a /= b |
| Целая часть | a = a // b | a //=b |
| Остаток | a = a % b | a %= b |
Деление на ноль
Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.
Исключение следует обрабатывать, это можно сделать так:
Арифметические действия в языке Си
Пожалуйста, приостановите работу AdBlock на этом сайте.
Программы работают с данными. Зачастую данные представляют собой числа. В этом уроке, как вы наверное догадались, мы будем заниматься изучением того, как и что в языке Си можно делать с числами. Начнём с арифметики.
Компилятор языка Си понимает все основные арифметические операции, которые вам известны со школы. Плюс есть несколько дополнительных.
Основные арифметические операторы языка Си.
+ оператор сложения
— оператор вычитания
* оператор умножения
% оператор взятия остатка от деления
/ оператор деления
Результат работы этой программы представлен на следующем рисунке.
Рис.5 Использование арифметических действий в Си.
Как видите, результат получился не тот, что мы ожидали. Это одна из особенностей оператора деления в языке Си.
При делении значение целого типа на значение целого типа результат тоже получается целого типа.
Так уж устроен язык Си. Поэкспериментируйте, попробуйте любые другие целые числа.
Вычислить результат целочисленного деления легко. Поделите числа и отбросьте всё, что получилось в дробной части.
Пример: Как получить результат целочисленного деления
7/2 = 3.5 → 3
11/3 = 3.66 → 3
2/5 = 0.4 → 0
Посмотрим на нашем примере:
Явное преобразование (приведение) типа.
Если какое-то значение нужно привести к другому типу, нужно перед этим значением в скобках написать название требуемого типа.
Листинг 4. Примеры явного преобразования типа
Важный момент: преобразуется не тип исходной переменной, а только лишь значение, которое используется в выражении. В следующем видео-фрагменте об этом говорится подробнее.
Обратите внимание, что, когда мы преобразовываем целое значение в вещественное, ничего особенного не происходит, т.к. вещественные числа включают в себя целые.
Совсем иная ситуация, когда мы от вещественного переходим к целому. При этом переходе у нас теряется вся дробная часть. Не забывайте об этом.
Картинка, показывающая различия между операциями взятие остатка, целочисленного деления и обычного деления.
Рис.2 Деление, целочисленное деление и остаток от деления.
Практика
Решите предложенные задачи:
Для удобства работы сразу переходите в полноэкранный режим
Исследовательские задачи для хакеров