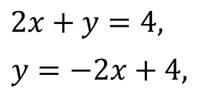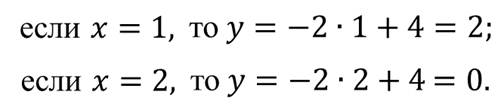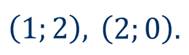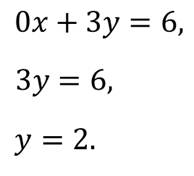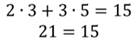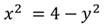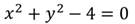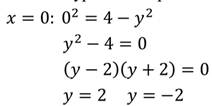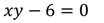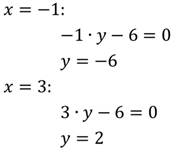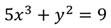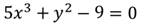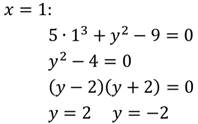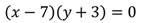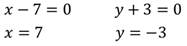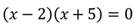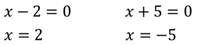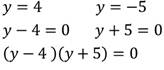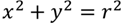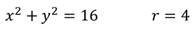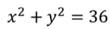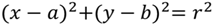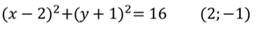Что является графиком уравнения с двумя переменными

Алгебра. 9 класс

Рассмотрим уравнение 3x 2 + y = 13.

Это уравнение является уравнением с двумя переменными x и y.

При подстановке вместо переменной x числа 2, а вместо переменной y числа 1 мы получим верное равенство.

Значит, пара чисел 2 и 1 является решением данного уравнения. Эту пару чисел записывают в круглых скобках, причём на первом месте записывают значение переменной x, а на втором – значение переменной y: (2; 1).

Итак, сформулируем определение решения уравнения с двумя переменными.

Решением уравнения с двумя переменными называется пара значений переменных, обращающая уравнение в верное равенство.

Если все эти пары чисел представить как координаты точек и изобразить на координатной плоскости, то получится график данного уравнения.

Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

Вспомним, что является графиком линейного уравнения с двумя переменными.

Графиком этого уравнения является окружность с центром в точке с координатами (а; b) и радиусом r.

Все пары чисел, которые будут являться решением данного уравнения, при изображении их на координатной плоскости будут принадлежать окружности с центром в точке с координатами (1; 2) и радиусом, равным 3.

Источник

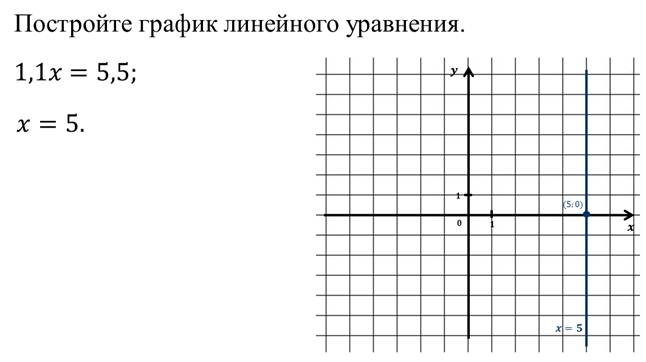
График линейного уравнения с двумя переменными

Урок 40. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «График линейного уравнения с двумя переменными»

· ввести понятие «график линейного уравнения с двумя переменными»;

· рассмотреть поведение графика в зависимости от значений коэффициентов перед переменными.

На прошлом уроке мы с вами познакомились с линейным уравнением с двумя переменным. Давайте, вспомним определение.

И сегодня на уроке мы будем вести речь о графике такого уравнения.

Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

Обратите внимание, что полученная формула имеет вид линейной функции, графиком которой является прямая.

Так как прямая определяется двумя точками, то для построения графика нам достаточно указать две точки. Так:

Таким образом, получили две точки с координатами:

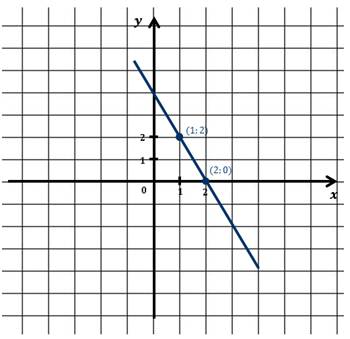
Теперь на координатной плоскости отметим эти точки и проведём через них линию.

Эта прямая является графиком исходного уравнения.

Все точки, принадлежащие графику, – это пары чисел, которые являются решениями нашего уравнения.

Теперь рассмотрим уравнение, в котором коэффициент при одной из переменных равен нулю.

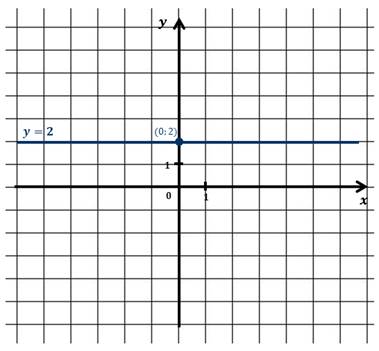
А это постоянная функция. С предыдущих уроков нам известно, что график такой функции – это прямая, которая проходит через точку с координатами (0; 2) и параллельна оси Ox.

Все точки, принадлежащие этой прямой, – это пары чисел, которые являются решениями данного уравнения. И таких решений бесконечно много.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

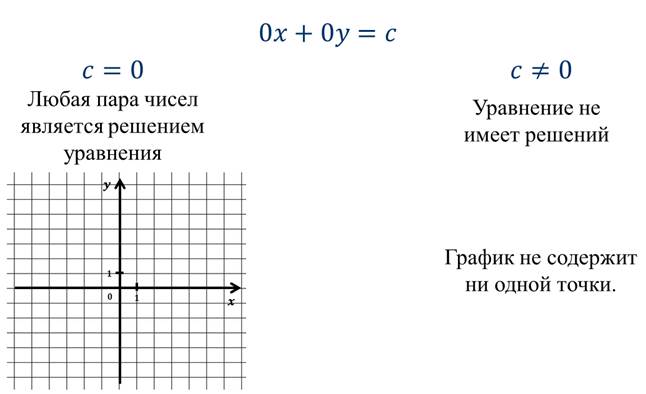
А теперь давайте рассмотрим случай, когда в линейном уравнении оба коэффициента при переменных равны нулю.

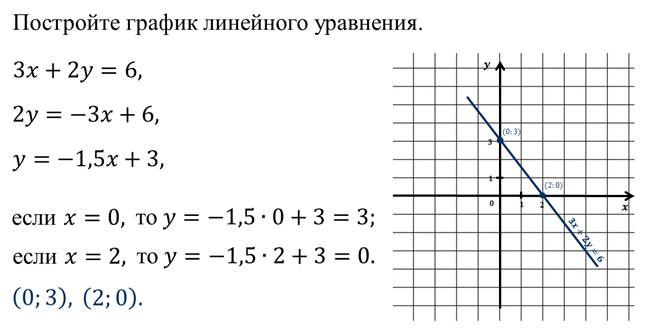
Давайте, рассмотрим примеры построения графиков линейных уравнений.

Итак, сегодня на уроке мы выяснили, что же представляет собой график линейного уравнения с двумя переменными и научились строить такие графики.

Источник

Уравнение с двумя переменными и его график

Урок 15. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Уравнение с двумя переменными и его график»

· уравнения с двумя переменными;

· решения уравнения с двумя переменными;

· степень уравнения с двумя переменными;

· график уравнения с двумя переменными.

Перед вами записаны уравнения:

Все они являются уравнениями с двумя переменными, так как в каждом из них есть две переменные. Возьмём, например, первое уравнение и подставим в него x=3 и y=5:

Получили неверное равенство. А если подставим x=3 и y=3, то получим верное числовое равенство.

Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное числовое равенство.

Пара чисел (3; 3) является решением данного уравнения. Но это не единственное решение.

Для определения степени уравнения с двумя переменными, нужно преобразовать его так, чтобы в левой части стоял многочлен стандартного вида, а справа ноль. Тогда степень уравнения считают равной степени данного многочлена.

Чтобы определить степень многочлена с двумя переменными, нужно определить степень каждого одночлена, входящего в состав многочлена, и выбрать из них наибольшую. Степень данного уравнения равна 1.

Определить степени уравнений и найти любых два решения.

1. Рассмотрим уравнение:

Степень данного уравнения равна 2.

Найдём два любых решения:

2. Решить уравнение:

Степень уравнения равна 2.

Найдём два решения уравнения:

3. Решить уравнение:

Степень данного уравнения равна 3.

Найдём любые два решения:

В ходе выполнения заданий стало понятно, что уравнения с двумя переменными имеют много решений. И указать все решения достаточно сложно. Если решением является пара значений, то его можно изобразить на координатной плоскости в виде точки. Так все решения и образуют график уравнения с двумя переменными.

Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

1. Построить график уравнения:

Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:

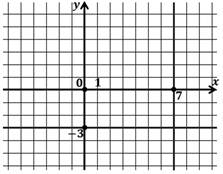
Изобразим график данного уравнения:

Решением являются две прямые: х=7 и у=-3.

2. Построить график уравнения:

Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:

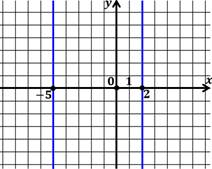
Изобразим график данного уравнения:

Решением являются две прямые: х=-5 и х=2.

Составить уравнения, графиками которых являются пары прямых, изображённых на рисунках.

Посмотрим на первый рисунок:

Получили, что прямые являются графиком уравнения.

Обратимся ко второму случаю:

Получили, что эти прямые являются графиком уравнения.

Графиком уравнения является окружность с центром в точке начала координат и радиусом r.

Например, графиком уравнения:

является окружность с r=4.

Записать уравнение окружности с центром в точке начала координат и r=6.

Получим уравнение окружности:

Если центром окружности не является точка начала координат, то уравнение окружности будет выглядеть так:

Центр окружности имеет координаты (a; b).

Выполним обратное действие. Но для записи уравнения окружности уже не достаточно только координат центра, необходимо знать и радиус. Например:

Источник

Уравнения с двумя переменными

Содержание:

Уравнения с двумя переменными — это решение системы двух линейных уравнений с двумя неизвестными с парой чисел (x,y), если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство.

Решение уравнения с двумя переменными. График уравнения с двумя переменными

Рассмотрим уравнение с двумя переменными f(x; у) = 0. Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения. Если дано уравнение с двумя переменными х и у, то принято в записи его решения на первое место ставить значение переменной х, а на второе — значение у.

Уравнения с двумя переменными называют равносильными, если они имеют одни и те же решения (или оба не имеют решений).

Для уравнений с двумя переменными справедливы теоремы 1 и 2 (см. п. 135) о равносильных преобразованиях уравнения.

Пусть дано уравнение с двумя переменными f(х; у) = 0. Если все его решения изобразить точками на координатной плоскости, то получится некоторое множество точек плоскости. Это множество называют графиком уравнения f(х; у) = 0.

Линейное уравнение с двумя переменными и его график

Уравнение вида , где х, у — переменные, а — числа, называют линейным; числа называют коэффициентами при переменных, с — свободным членом.

Графиком любого линейного уравнения , у которого хотя бы один из коэффициентов при переменных отличен от нуля, является прямая; если , то эта прямая параллельна оси у, если , то эта прямая параллельна оси х.

Пример:

Решение:

Если линейное уравнение имеет вид 0 * х + 0 * у = с, то могут представиться два случая:

1) с = 0; в этом случае уравнению удовлетворяет любая пара ( х; у), а потому графиком уравнения является вся координатная плоскость;

2) в этом случае уравнение не имеет решения; значит, его график не содержит ни одной точки.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник

Линейные уравнения с двумя переменными

Линейные уравнения с двумя переменными

Определение: Решение уравнения с двумя переменными – это пара значений переменных, обращающая это уравнение в верное равенство.

т. е. пара чисел (4; 1,5) не является решением уравнения.

Определение: Равносильные уравнения – это уравнения, имеющие одни и те же решения или не имеющие их.

1. В уравнении можно перенести слагаемое из одной части уравнения в другую, изменив его знак.

2. Обе части уравнения можно множить или разделить на одно и то же отличное от нуля число.

Выразить одну переменную через другую:

1) 2х +у = 5 2) 3)

График линейного уравнения с двумя переменными

Определение: График уравнения с двумя переменными – это множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

1. Пример: 3х + 2у = 6, где а=3, b=2, c=6

План 1) Выразить переменную у

у =

2) Составить таблицу значений х и у

3) Построить график

2. Частные случаи построения графика ax + by = c

у =

x =

х = 2

Графика не существует

График – вся координатная плоскость

Решение систем уравнений с двумя переменными. Графический способ.

Определение: Система уравнений – это несколько уравнений, для которых находят общее решение.

Определение: Решение системы уравнений с двумя переменными – это пара значений переменных, обращающая каждое уравнение в верное равенство.

Если х=7, у=5, то , , верно,

т. е. (7; 5) – решение системы уравнений.

Определение: Решить систему – это значит найти все ее решения или доказать, что решений нет.

План решения системы уравнений графическим способом

1. Выразить переменную у в первом уравнении.

2. Выразить переменную у во втором уравнении.

3. В одной системе построить графики данных функций.

4. Координаты точки пересечения графиков и является решением системы уравнений.

Пример:

Источник