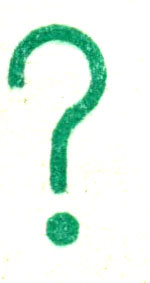Что является изометрической проекцией окружности

Черчение. 10 класс

§ 18. Построение аксонометрических проекций плоских фигур и окружностей

Построение аксонометрических проекций плоских фигур и окружностей

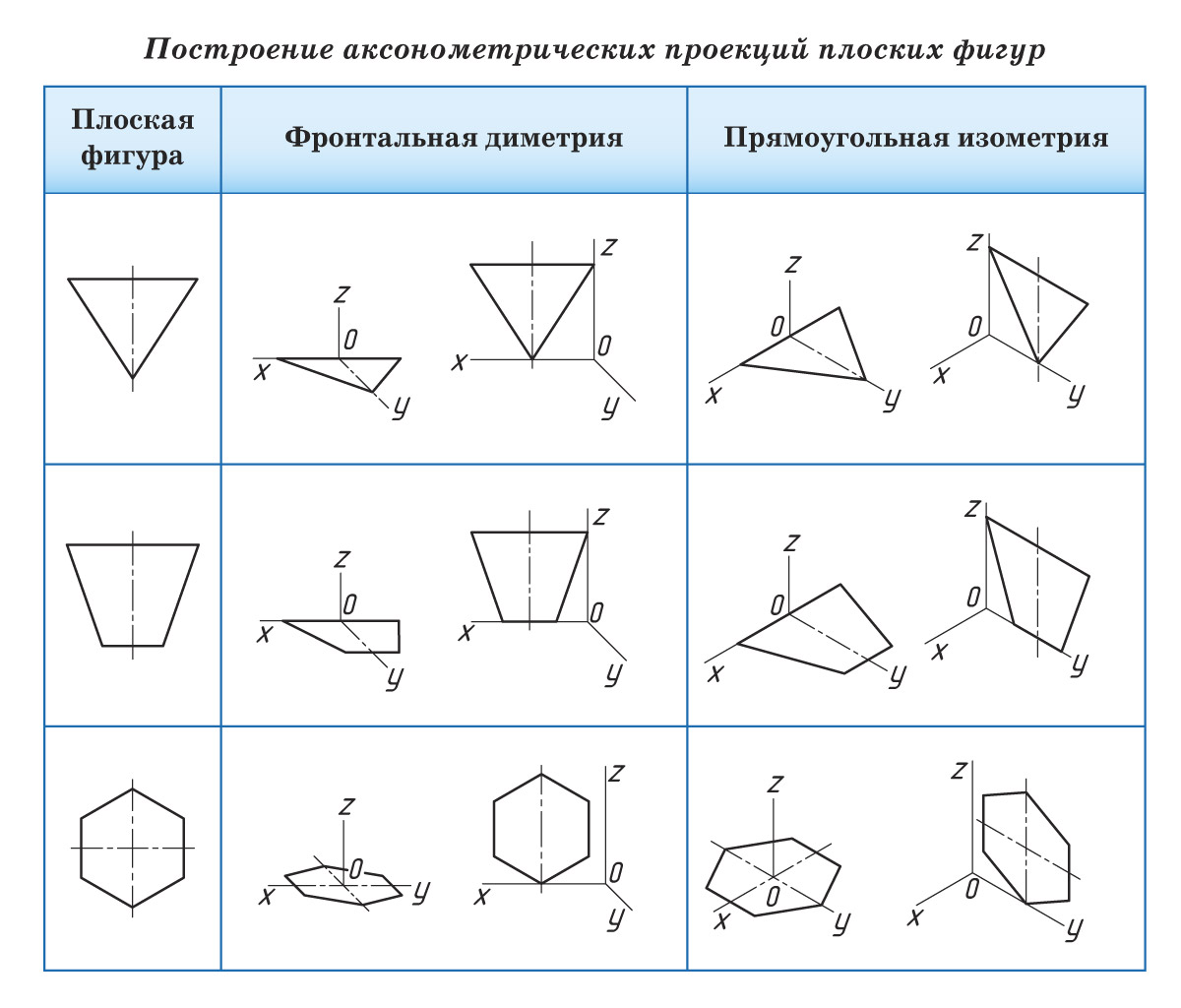
Построение аксонометрических проекций мы начнем с построения аксонометрических проекций плоских геометрических фигур. Знание приемов построения плоских фигур (квадрата, треугольника, прямоугольника, круга) необходимо для построения аксонометрических проекций геометрических тел, предметов и т. д.

Плоская фигура — фигура, все точки которой находятся в одной плоскости .

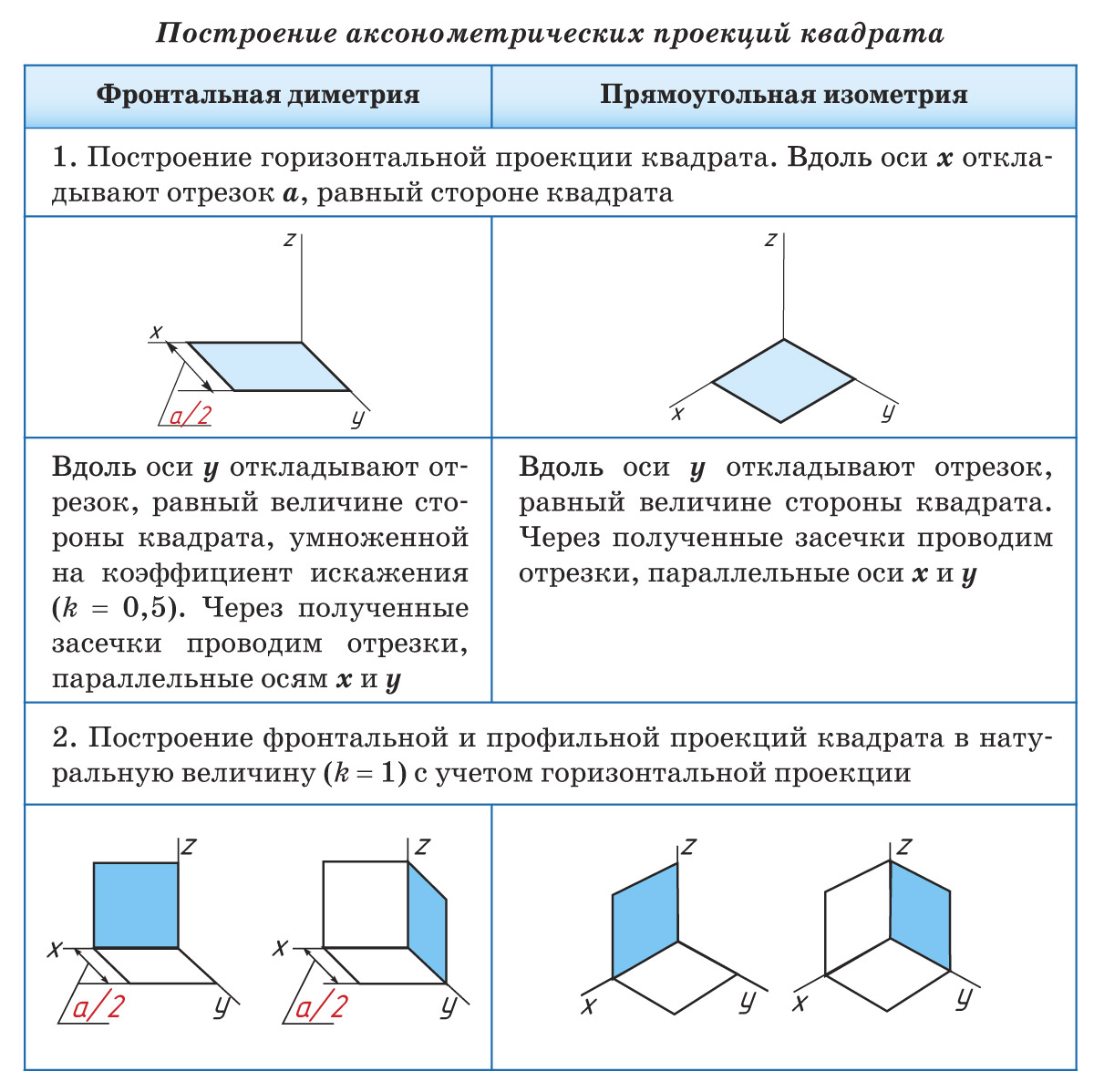
В качестве примера рассмотрим алгоритм построения аксонометрической проекции квадрата. По такому же алгоритму строятся аксонометрические проекции других плоских многоугольников.

На основе алгоритма построения квадрата постройте аксонометрические проекции прямоугольного треугольника. Какая сторона треугольника будет проецироваться с искажением во фронтальной диметрии?

Постройте аксонометрические проекции елки. Какие плоские фигуры составляют изображение? Какой плоскости проецирования елка параллельна?

Кроме многоугольников, к плоским фигурам относят и окружности. В изометрической проекции окружность проецируется в замкнутую кривую линию — эллипс (рис. 55). Для его построения пользуются лекалами, поэтому эллипсы называют лекальными кривыми. Прием построения эллипса сложный и требует длительной работы, поэтому для упрощения построений эллипсы заменяют овалами.

Овал — замкнутая кривая, состоящая из четырех дуг окружностей, плавно переходящих друг в друга (рис. 56).

Для удобства построения овала в аксонометрической проекции сначала изображают аксонометрическую проекцию квадрата, построение которой вам уже известно.

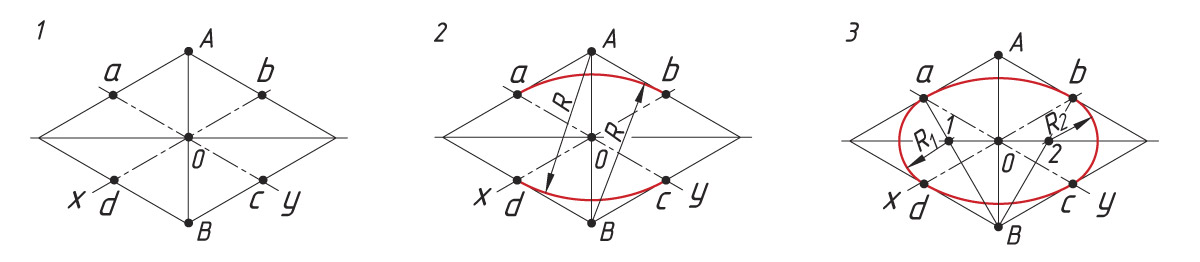
Общее построение аксонометрической проекции окружности

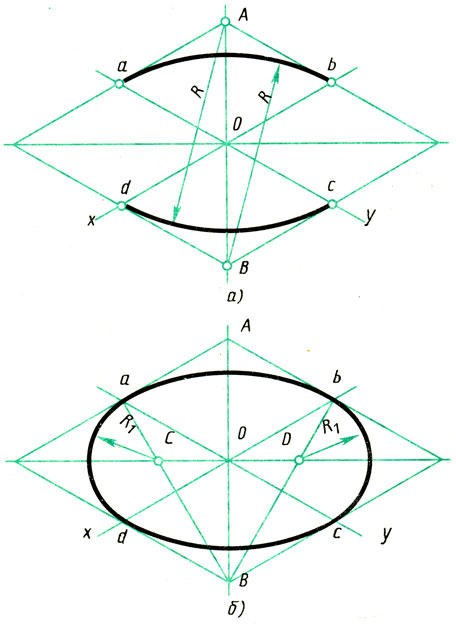
1. Выполняют построение осей аксонометрической проекции. Затем от точки О откладывают отрезки, равные радиусу окружности (R = Oa = Ob = Oc = Od). Через точки а, b, c и d проводят прямые, параллельные осям, получают ромб. Большая ось овала располагается на большой диагонали ромба.
2. Выполняют построение больших дуг овала. Из вершин А и В описывают дуги радиусом R, равные расстоянию от вершины (А или В) до точек a, b, c, d (R = Ad = Bb).
3. Строят малые дуги овала. Через точки B и a, B и b проводят прямые. На пересечении прямых Вa и Вb с большой диагональю ромба находят точки 1 и 2. Они будут центрами малых дуг. Их радиус R1 равен 1а или 2b

Построение фронтальной и профильной проекций окружности
Фронтальная и профильные проекции окружности выполняются по такому же алгоритму, как и горизонтальная проекция.

Помните! Большая ось овала всегда перпендикулярна аксонометрической оси, не участвующей в образовании плоскости, на которой ведется построение. Малая ось — продолжение аксонометрической оси.

Определите, на каком рисунке (а или б) изображен куб в изометрии. Объясните, как вы это определили.

Эллипсограф, или Сеть Архимеда, — механизм, который способен преобразовывать возвратно-поступательное движение в эллипсоидное. Применяется в качестве чертежного инструмента для вычерчивания эллипсов, а также в качестве приспособления для разрезания стекла, бумаги, картона. История этого механизма точно не определена, но считается, что эллипсографы существовали еще во времена Архимеда.

Источник

Изображение кругов в изометрических и диметрических проекциях

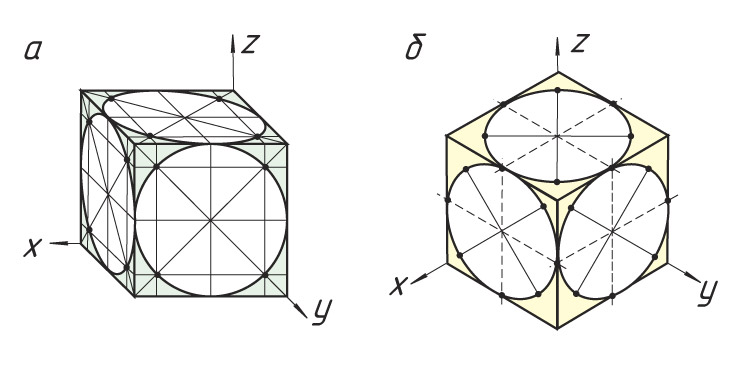
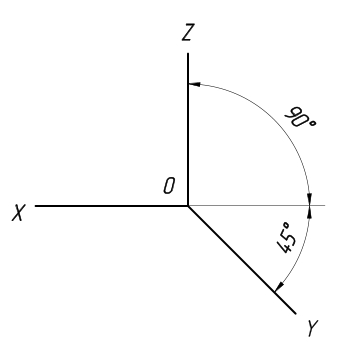
Из геометрии известно, что круг можно рассматривать как правильный многоугольник с большим количеством сторон. Следовательно, изометрическое изображение круга можно строить так же, описывая вокруг него квадрат (рис. 155, а). Точки касания А, В, С и D будут находиться на средине сторон квадрата и легко могут быть нанесены на аксонометрическое изображение (рис. 155, б). Промежуточные точки Е’, F’ и другие находим с помощью их координат. Изометрической проекцией круга является эллипс; его большая ось EG расположена под углом 60° к горизонту по большой диагонали ромба, а малая ось — под углом 30° по малой диагонали ромба.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451018_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Аксонометрические изображения круга чаще строят, проводя оси х и у через центр окружности (рис. 156, а); при этом отпадает надобность в построениях квадрата и ромба. Выбрав точку О’, проводим через нее оси х’ и у’ (рис. 156, б), откладываем на осях величины, равные радиусу окружности, получаем точки А’, В’, С и D’. Другие точки находим с помощью их координат; построение точки Е показано двойными тонкими линиями. Два координатных отрезка для точки Е составляют так называемую координатную ломаную, которая будет в дальнейшем широко применяться при построении точек, расположенных в пространстве. Большая ось эллипса E’G’ для круга, лежащего в плоскости х’О’у’, расположена горизонтально, а малая ось — вертикально.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451012_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

В начертательной геометрии доказывается, что отношение осей эллипса, являющегося изображением окружности, в прямоугольной изометрии равняется 0,58, т. е. если большую ось эллипса d принять за единицу, то малая ось будет равна 0,58d. Это положение иллюстрируем так: расположим плоскость квадрата, в который вписана окружность, параллельно плоскости П₂ (рис. 157, а); повернем квадрат вокруг его горизонтальной диагонали на угол, равный 54° 30′ (рис. 157, б); спроецируем квадрат и окружность на плоскость, параллельную горизонтальной диагонали квадрата (рис. 157, е). Диагональ ромба и горизонтальный диаметр окружности спроецируются при этом в действительную величину, стороны ромба изобразятся прямыми, составляющими =0,82 от величины d; наклоненные диагональ и диаметр окружности спроецируются с искажением и составят 0,58 от своей действительной величины, поскольку sin 35°30′ = 0,58.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451023_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Изображение окружности на рис. 157, в является натуральным. Чтобы перейти к «приведенному» изображению, которое, как известно, увеличено в 1,22 раза, умножим все три величины на указанное количество раз. Получим: сторона ромба 0,82dxl,22 = 1,004d = d; большая ось эллипса dx 1,22 = 1,22d; малая ось эллипса 0,58dx1,22= 0,71d.

Зная эти зависимости, мы можем по заданному диаметру круга быстро найти размеры большой и малой осей эллипса, являющегося изометрической проекцией окружности. Пусть требуется построить прямоугольную изометрию круга, диаметр окружности которого равен 50 мм. Определяем размеры большой и малой осей эллипса: большая ось А’В’ равна 50х X 1,22 = 61 мм, малая ось CD’ равна 50’х0,71=35 мм. Строим по этим размерам оси эллипса на чертеже (рис. 158, а).

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451055_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Из геометрического черчения известно (см. рис. 47), что по осям эллипса можно построить его кривую. Практически эллипс в изометрии обычно заменяют овалом, который строят следующим образом (рис. 158, б). На большой А’В’ и малой CD’ осях строим две окружности; они пересекают продолжение малой оси в точках 1 и 2, а большую ось — в точках 3 и 4; эти точки являются центрами для дуг овала; используя их, вычерчиваем овал с радиусами r = О’В’—О’С и R = CD’ + г. Точку сопряжения дуг радиусов R и г находим, соединяя точки 1 и 4 прямой и продолжая эту прямую до пересечения с дугами в точке 5.

В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу и лишь расположены различно. В отличие от этого в прямоугольной диметрии имеются две различные формы эллипса: одна для плоскости х’О’z’, а другая — для плоскостей х’О’у’ и z’O’y’.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451008_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Пусть требуется построить прямоугольную диметрию окружности, лежащей в плоскости хОz (рис. 159, а). Описываем вокруг окружности квадрат и проводим его диагонали. Отмечаем точки пересечения диагоналей с окружностью и координатные отрезки, нужные для построения точек Е, F и др. Строим квадрат в прямоугольной диметрии (рис. 159, б), проводим его средние линии А’С и B’D’ и диагонали. Пользуясь координатными отрезками (помечены на чертежах тонкими двойными линиями), находим точки Е’, F’, G’ и H’. Большая ось эллипса F’G’ в прямоугольной диметрии будет равна l,06d, малая ось Е’Н’ будет равна 0,95d (отношение 9 : 10). Полученные восемь точек соединяем от руки, а затем обводим по лекалу. Если требуется более точное построение, то находят с помощью координатных ломаных еще ряд промежуточных точек.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451062_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

В практике эллипс нередко заменяют овалом (рис. 160, а). Центры дуг для построения овала находим так: строим ромб, его средние линии и диагонали, Из центра О’ радиусом r=d/7 проводим вспомогательную окружность.

Она пересекает малую диагональ ромба в точках 1 и 2; используем эти центры для проведения дуг А’В’ и CD’. Соединяем точки А’ и I, С и 2; эти линии пересекают большую диагональ в точках 3 и 4. Пользуясь этими центрами, проводим дуги A’D’ и В’С. При этом способе также не требуется откладывать размеры большой и малой осей; они получаются сами собой при проведении дуг.

Если требуется построить прямоугольную диметрию окружности, лежащей в плоскости х’О’у’, то на осях х’ и у’ строим параллелограмм и намечаем средние точки его сторон (рис. 160, б). Затем через точку О’ проводим горизонтальную прямую — направление большой оси эллипса. Откладываем на этой прямой размер большой оси эллипса, равный 1,06d. Перпендикулярно к ней проводим малую ось эллипса, размер которой равен 0,35d (отношение 3 : 10). Таким путем получаем восемь точек, принадлежащих эллипсу. В практике избегают построения параллелограмма и строят вместо эллипса овал по его осям А’В’ и CD’ (рис. 160, в). Последовательность построения такая: от центра О’ на продолжении малой оси эллипса откладываем величину большой оси А’В’; получаем точку 1 — центр верхней дуги радиуса R. Тем же радиусом из точки 2 (не показана на чертеже) проводим нижнюю дугу овала. Слева и справа овал дочерчиваем кривыми радиуса r, величину которого принимаем равным r=O’C’/2 Центры 3 и 4 находим, делая засечки дугами r из точек А’ и В’. Точку сопряжения 5 находим, соединяя прямой точки I и 4 и продолжая эту прямую до пересечения с дугой.

Окружность, находящаяся в плоскости, параллельной фронтальной плоскости проекций, проецируется на нее во фронтальной изометрической проекции в виде окружности (рис. 161, а), а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, — в эллипсы, большие оси которых наклонены к осям х’ и z’ под углами 22° 30′. Большие оси эллипсов равны 1,3 диаметра окружности, малые — 0,54 диаметра окружности.

Пусть требуется построить во фронтальной изометрии окружность диаметра 40 мм, находящуюся в плоскости х’О’у’. Определяем большую и малую оси эллипса. Большая ось А’В’ = 1,3d = 1,3 40 = 52 мм, малая ось CD’ = 0,54d = 0,54-40 = 21,6 мм. Овал, заменяющий собой эллипс, удобно строить из четырех центров радиусами, равными R = 1,3d и r = = 0,16d (рис. 161, б). В нашем примере R — 52 мм, г = 0,16d = 6,4 мм. Точка 5 — точка сопряжения.

Источник

Аксонометрические проекции

Для того чтобы наиболее наглядно передать форму изделий и предметов, ясно и понятно представить схемы взаимодействия различных деталей, по мере надобности применяются аксонометрические проекции.

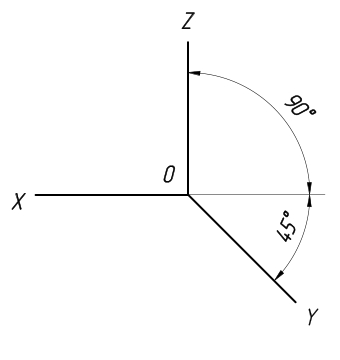
Прямоугольная изометрическая проекция

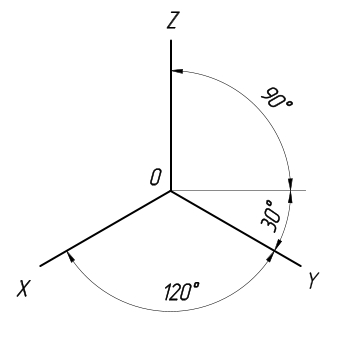
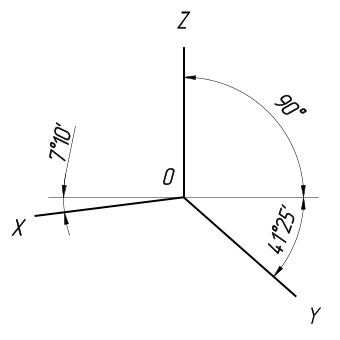
Проекция этого вида отличается тем, что в ней оси аксонометрии располагаются друг по отношению к другу под углом 120°. При этом искажения изображения по всем аксонометрическим осям имеют один и тот же коэффициент, равный 0,82.

Чтобы упростить изометрическую проекцию, по осям x, y и z, как правило, выполняют без искажений, то есть его коэффициент выбирают равным единице.

Изображение окружностей в прямоугольной изометрии

Если окружности располагаются в тех плоскостях, которые параллельны плоскостям проекций, то в аксонометрической плоскости они изображаются в виде эллипсов.

В тех случаях, когда по осям x, y, и z изометрическая проекция выполняется без искажений, длина большой и малой осей эллипсов составляет, соответственно, 1,22 и 0,71 от диаметра отображаемой окружности.

В тех случаях, когда по осям x, y и z изометрическая проекция выполняется с искажениями, длина большой оси эллипсов равняется диаметру отображаемой окружности, а длина малой оси – 0,58 от нее.

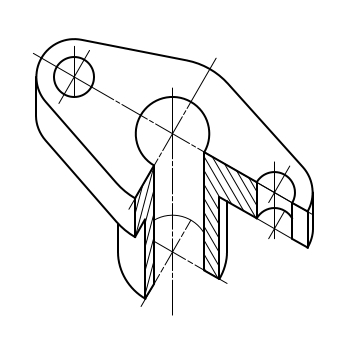
Изображение детали в прямоугольной изометрии

Чтобы наиболее наглядно передать особенности формы различных изделий и предметов, их изображают в прямоугольной изометрической проекции.

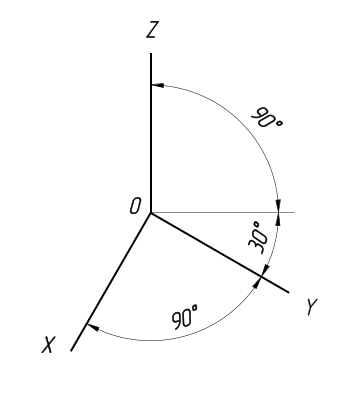
Прямоугольная диметрическая проекция

Отличительной особенностью прямоугольной диметрической проекции является то, что она имеет различные коэффициенты искажения по разным аксонометрическим осям: для x и z он имеет значение 0,94, а по y, равна значению 0,47.

В большинстве случаев диметрическая проекция выполняется с коэффициентом искажения по оси аксонометрии y, равным 0,5, и по осям аксонометрии z и x, равным единице.

Изображение окружностей в прямоугольной диметрии

Те окружности, которые располагаются в плоскостях, являющихся параллельными по отношению к плоскости проекции, при проецировании на аксонометрическую плоскость изображаются в виде эллипсов.

В тех случаях, когда диметрическая проекция окружности выполняется в неискаженном виде по осям z и x, длина большой оси эллипсов составляет 1,06 от диаметра изображаемой окружности, при этом малая ось эллипса под номером 1 ровна 0,95, а эллипсов под номерами 2 и 3 ровна 0,35 диаметра окружности.

В тех случаях, когда диметрическая проекция окружности выполняется в искаженном виде по осям x и z, длина больших осей всех эллипсов соответствует диаметру окружности, малой оси эллипса под номером 1 равна 0,9, а эллипсов с номерами 2 и 3 равна 0,33 длины диаметров окружности.

Изображение детали в прямоугольной диметрии

Для того чтобы в печатных изданиях и на некоторых других видах носителей информации представить деталь или изделие наиболее наглядно, ее изображают в прямоугольной диметрии.

Косоугольная фронтальная изометрическая проекция

Для этой проекции характерно то, что проекции с углом наклона оси у допускается располагать с углом наклона от 30° до 60°. Фронтальная изометрическая проекция по осям x, y и z искажений не имеет.

Изображения окружности в косоугольной фронтальной изометрии

Те окружности, которые располагаются в плоскостях, лежащих параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в виде окружностей. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и горизонтальной плоскостям проекций, проецируются в эллипсы. При этом длина их больших осей составляет 1,3 диаметра окружности, а малой оси – 0,54 диаметра окружности.

Изображение детали в косоугольной фронтальной изометрии

Изображение деталей в косоугольной фронтальной изометрии, используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

Косоугольная горизонтальная изометрическая проекция

Отличительной особенностью косоугольной горизонтальной изометрической проекции является то, что здесь допускается применять, что проекции с углом наклона оси у допускается располагать под углом наклона от 45° до 60°, при этом угол 90° между осями x и y должен сохраняться неизменным. В данной проекции искажения отсутствуют по всем осям.

Изображения окружности в косоугольной горизонтальной изометрической проекции

Те окружности, которые располагаются в плоскостях, находящихся параллельно горизонтальной плоскости проекций, на аксонометрическую плоскость проецируются в окружности. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и фронтальной плоскостям проекций, проецируются в эллипсы.

Наибольшая ось эллипса под номером 1 равна 1,37, а малая ось равна 0,37 от диаметра окружности. Большая ось эллипса номер 3 равна 1,22, а малая ось равна 0,71 от диаметра окружности.

Изображение детали в косоугольной горизонтальной изометрии

Эта проекция используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

Косоугольная фронтальная диметрическая проекция

Отличительной чертой этой проекции является то, что аксометрическая ось y может иметь угол наклона от 30° до 60°. При этом коэффициент искажения по осям x и z равняется единице, а по оси y – 0,5.

Изображения окружности в косоугольной фронтальной диметрии

Те окружности, которые располагаются в плоскостях, находящихся параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в окружности. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и горизонтальной плоскостям проекций, проецируются в эллипсы. При этом длина их больших осей составляет 1,07 диаметра окружности, а малой оси – 0,33 диаметра окружности.

Изображение детали в косоугольной фронтальной диметрии

Эта проекция используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

Нанесение размеров

Размерные линии при изображении аксонометрических проекций должны наноситься параллельно измеряемым отрезкам, а выносные – параллельно аксонометрическим осям.

Штриховка

Сечения во всех аксонометрических проекциях наносится штриховкой. При этом ее линии должны быть параллельны лежащим в соответствующих координатных плоскостях диагоналям проекций квадратов.

Источник

Что является изометрической проекцией окружности

§ 14. Построение аксонометрических проекций окружности

Рассмотрите рис. 92. На нем дана фронтальная диметрическая проекция куба с вписанными в его грани окружностями.

Рис. 92. Фронтальные диметрические проекции окружностей, вписанных в грани куба

Окружности, расположенные на плоскостях, перпендикулярных к осям х и z, изображаются эллипсами. Передняя грань куба, перпендикулярная к оси у, проецируется без искажения, и окружность, расположенная на ней, изображается без искажения, т. е. описывается циркулем. Поэтому фронтальная диметрическая проекция удобна для изображения предметов с криволинейными очертаниями, подооных представленными на рис. 93.

Рис. 93. Фронтальные диметрические проекции деталей

Построение фронтальной диметрической проекции плоской детали с цилиндрическим отверстием. Фронтальную диметрическую проекцию плоской детали с цилиндрическим отверстием выполняют следующим образом.

1. Строят очертания передней грани детали, пользуясь циркулем (рис. 94, а).

2. Через центры окружности и дуг параллельно оси у проводят прямые, на которых откладывают половину толщины детали. Получают центры окружности и дуг, расположенных на задней поверхности детали (рис. 94, б). Из этих центров проводят окружность и дуги, радиусы которых должны быть равны радиусам окружности и дуг передней грани.

Рис. 94. Построение фронтальной диметрической проекции детали с цилиндрическими элементами

3. Проводят касательные к дугам. Удаляют лишние линии и обводят видимый контур (рис. 94, в).

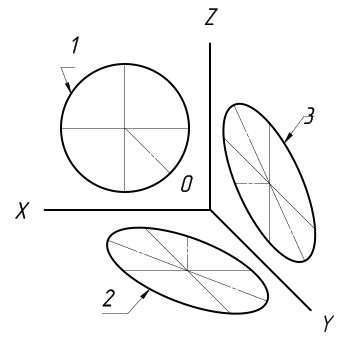
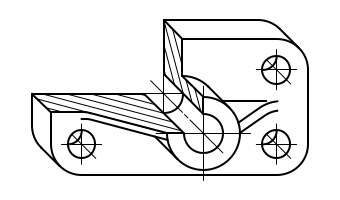
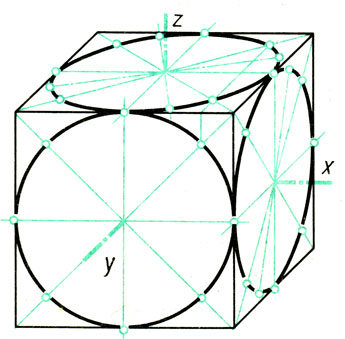
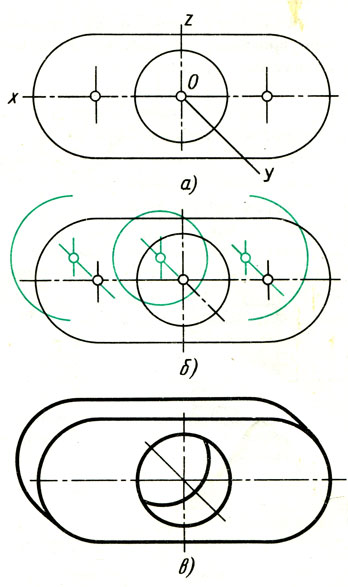
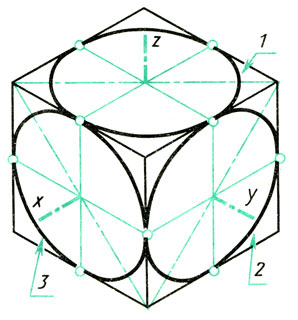
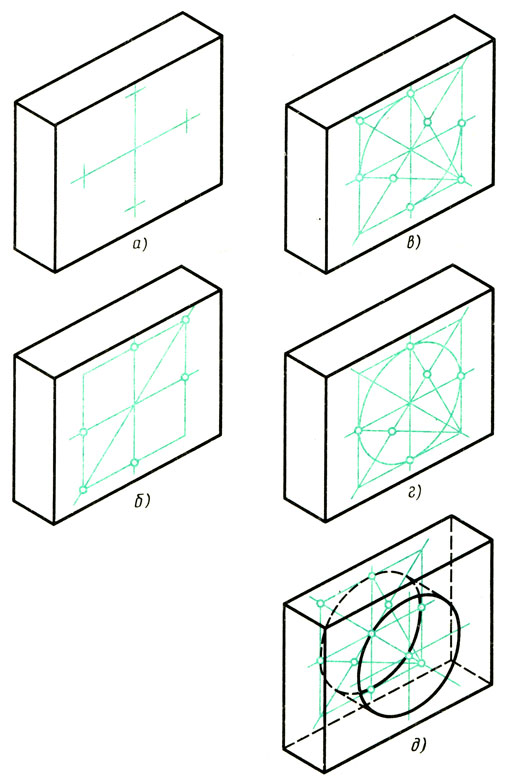
Изометрические проекции окружностей. Квадрат в изометрической проекции проецируется в ромб. Окружности, вписанные в квадраты, например, расположенные на гранях куба (рис. 95), в изометрической проекции изображаются эллипсами. На практике эллипсы заменяют овалами, которые вычерчивают четырьмя дугами окружностей.

Рис. 95. Изометрические проекции окружностей, вписанных в грани куба

Построение овала, вписанного в ромб.

1. Строят ромб со стороной, равной диаметру изображаемой окружности (рис. 96, а). Для этого через точку О проводят изометрические оси х и у и на них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки a, w, с и d проводят прямые, параллельные осям; получают ромб. Большая ось овала располагается на большой диагонали ромба.

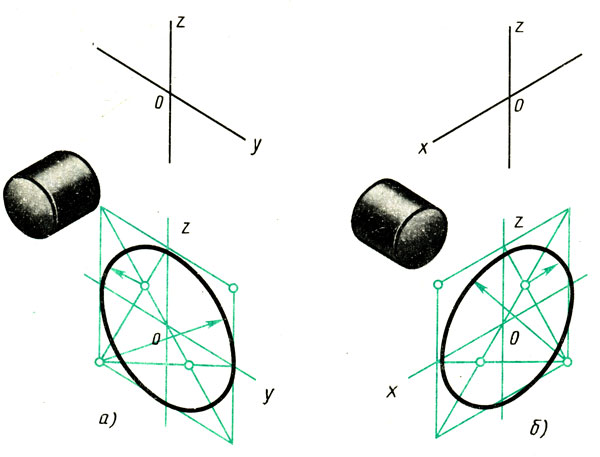
Рис. 96. Построение овала в плоскости, перпендикулярной оси z

Рис. 97. Построение овала в плоскостях, перпендикулярных осям х и у

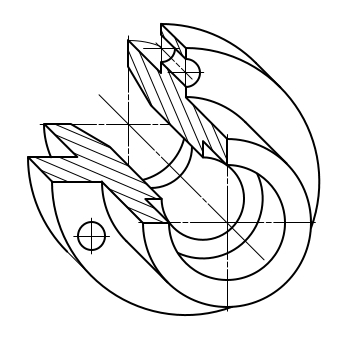
Построение изометрической проекции детали с цилиндрическим отверстием.

Как применить рассмотренные построения на практике?

Дана изометрическая проекция детали (рис. 98, а). Нужно изобразить сквозное цилиндрическое отверстие, просверленное перпендикулярно передней грани.

Построения выполняет следующим образом.

1. Находят положение центра отверстия на передней грани детали. Через найденный центр проводят изометрические оси. (Для определения их направления удобно воспользоваться изображением куба на рис. 95.) На осях от центра откладывают отрезки, равные радиусу изображаемой окружности (рис. 98, а).

2. Строят ромб, сторона которого равна диаметру изображаемой окружности; проводят большую диагональ ромба (рис. 98, б).

3. Описывают большие дуги овала; находят центры для малых дуг (рис. 98, в).

4. Проводят малые дуги (рис. 98, г).

5. Строят такой же овал на задней грани детали и проводят касательные к обоим овалам (рис. 98, д).

Рис. 98. Построение изометрической проекции летали с цилиндрическим отверстием

Ответьте на вопросы

1. Какими фигурами изображаются во фронтальной диме-трической проекции окружности, расположенные на плоскостях, перпендикулярных к осям х и у?

2. Искажается ли во фронтальной диметрической проекции окружность, если ее плоскость перпендикулярна оси у?

4. Какими фигурами изображаются в изометрической проекции окружности, расположенные на плоскостях, перпендикулярных к осям х, у, z?

5. Какими фигурами в практике заменяют эллипсы, изображающие окружности в изометрической проекции?

6. Из каких элементов состоит овал?

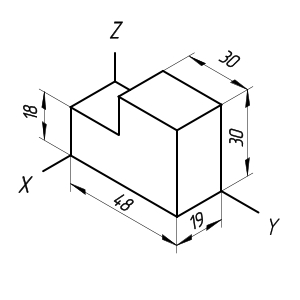
7. Чему равны диаметры окружностей, изображенных овалами, вписанными в ромбы на рис. 95, если стороны этих ромбов равны 40 мм?

Задания к § 13 и 14

Упражнение 42

Рис. 99. Задание для упражнений

Упражнение 43

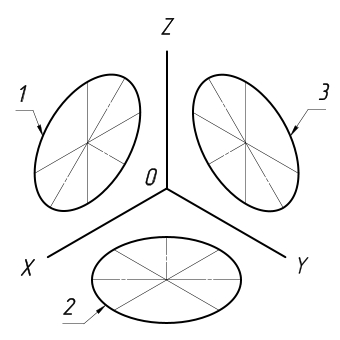
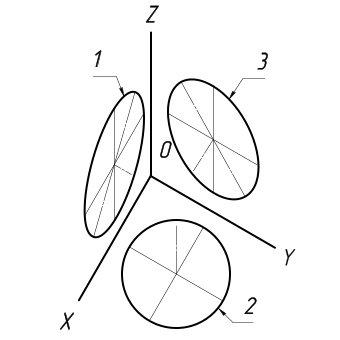
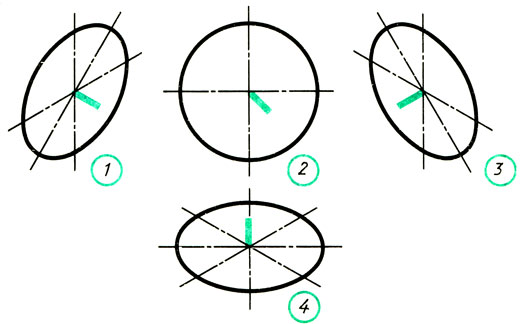
Запишите, какой оси (х, у или z) перпендикулярны плоскости овала на рис. 100. В какой аксонометрической проекции даны здесь окружности?

Рис. 100. Задание для упражнений

Упражнение 44

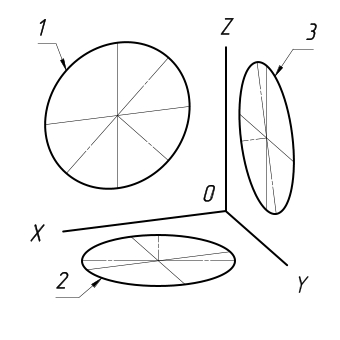
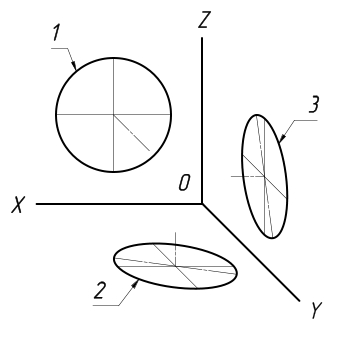
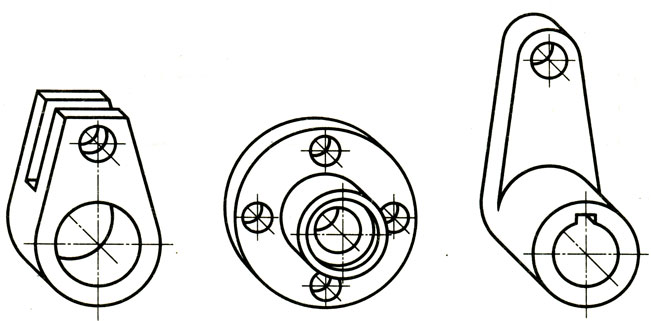
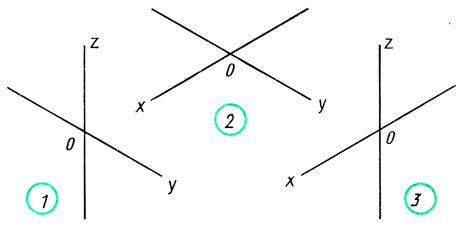
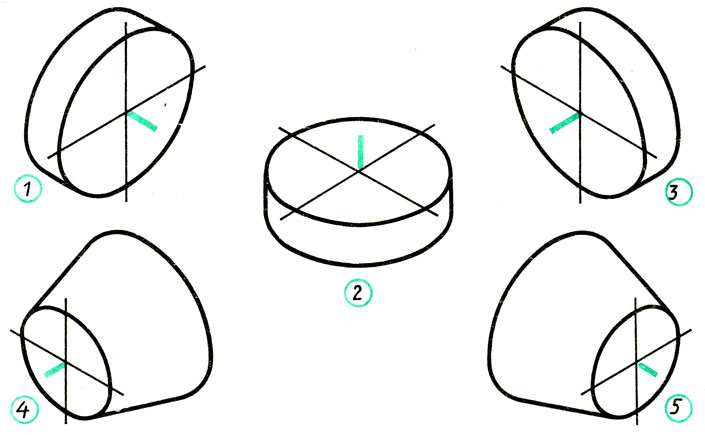
В каких аксонометрических проекциях даны окружности на рис. 101? Какой оси перпендикулярна плоскость каждой из них?

Рис. 101. Задание для упражнений

Упражнение 45

Запишите, в каких аксонометрических проекциях даны геометрические тела на рис. 102.

Каким осям (х, у или z) параллельна высота каждого из них?

Рис. 102. Геометрические тела для задания для упраждений

Упражнение 46

Источник