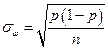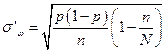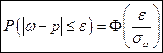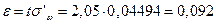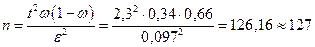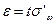Что является оценкой генеральной доли или вероятности

Тест по «Теории вероятности и математической статистике»

Автор работы: Пользователь скрыл имя, 30 Мая 2013 в 16:34, тест

Описание работы

Файлы: 1 файл

Externat_Teoria_veroyatnostey_i_matematicheskaya (9).docx

Ответ: распределение Стьюдента

При проверке гипотезы об однородности ряда вероятностей в случае полиномиального распределения используется:

Ответ: распределение Пирсона

При проверке значимости коэффициента корреляции с помощью таблицы Фишера-Иейтса коэффициент корреляции считается значимым, если:

Ответ: рассчитанное по выборке значение коэффициента корреляции превышает по модулю найденное по таблице критическое значение

Произведение каких событий есть событие невозможное?

Простой называют статистическую гипотезу:

Ответ: однозначно определяющую закон распределения

Симметричный ли интервал строится при оценивании генеральной дисперсии для заданной надѐжности γ?

Симметричный ли интервал строится при оценивании генеральной доли (вероятности) в случае большого объѐма наблюдений для заданной надѐжности γ?

Симметричный ли интервал строится при оценивании генеральной средней для заданной надѐжности γ?

Сколькими способами можно поставить 5 человек в очередь?

Сколькими способов жеребьѐвки существует для 5 участников конкурса?

Сколько различных двухбуквенных бессмысленных слов можно составить из букв К, Н, И, Г, А?

Сколько различных трѐхбуквенных бессмысленных слов можно составить из букв К, Н, И, Г, А?

Сложной называют статистическую гипотезу:

Ответ: не определяющую однозначно закон распределения

Согласно методу наименьших квадратов, в качестве оценок параметров двумерной линейной регрессионной модели следует использовать такие значения b0, b1, которые минимизируют сумму квадратов отклонений:

Ответ: фактических значений зависимой переменной от ее расчетных значений

Статистическим критерием называют:

Ответ: правило, устанавливающее условия, при которых проверяемую гипотезу следует либо отвергнуть, либо не отвергнуть

Статистической гипотезой называют предположение:

Ответ: о виде или параметрах неизвестного закона распределения случайной величины

Сумма каких событий есть событие достоверное?

Точечную оценку называют эффективной, если она:

Ответ: обладает минимальной дисперсией среди всех несмещенных оценок

У какого распределения случайной величины вероятности рассчитываются по формуле Бернулли?

У какого распределения случайной величины вероятности рассчитываются по формуле Пуассона?

Уравнение регрессии имеет вид ŷ=1,7+5,1x. На сколько единиц своего измерения в среднем изменится y при увеличении x на 1 единицу своего измерения:

Ответ: увеличится на 5,1

Уравнение регрессии имеет вид ŷ=1,7-5,1x. На сколько единиц своего измерения в среднем изменится y при увеличении x на 1 единицу своего измерения:

Ответ: уменьшится на 5,1

Уравнение регрессии имеет вид ŷ=5,1+1,7x. На сколько единиц своего измерения в среднем изменится y при увеличении x на 1 единицу своего измерения:

Ответ: увеличится на 1,7

Уравнение регрессии имеет вид ŷ=5,1-1,7x. На сколько единиц своего измерения в среднем изменится y при увеличении x на 1 единицу своего измерения:

Ответ: уменьшится на 1,7

Функция плотности вероятности непрерывной случайной величины есть … еѐ функции распределения

Функция распределения дискретной случайной величины есть функция:

Функция распределения любой случайной величины есть функция:

Функция распределения непрерывной случайной величины есть функция:

Функция распределения непрерывной случайной величины есть … еѐ функции плотности вероятности

Человек забыл последние две цифры номера телефона своего знакомого и, помня лишь, что они различны, пытается набрать номер наугад. Какова вероятность, что он дозвонится с первого раза?

Чем достигается репрезентативность выборки?

Ответ: случайностью отбора

Чему равна вероятность достоверного события?

Чему равна вероятность любого отдельно взятого значения непрерывной случайной величины?

Чему равна вероятность невозможного события?

Чему равна дисперсия постоянной величины?

Чему равна дисперсия случайной величины Y=2X+1, если дисперсия X равна 2?

Чему равна дисперсия случайной величины Y=2X+1, если дисперсия X равна 3?

Чему равна дисперсия случайной величины Y=2X-1, если дисперсия X равна 3?

Чему равна дисперсия случайной величины Y=2X-5, если дисперсия X равна 2?

Чему равна дисперсия случайной величины Y=2X-5, если дисперсия X равна 2?

Чему равна дисперсия случайной величины Y=3X+5, если дисперсия X равна 2?

Чему равна сумма вероятностей всех значений дискретной случайной величины?

Чему равна сумма доверительной вероятности (надѐжности) γ и вероятности α при использовании распределения Стьюдента?

Чему равно математическое ожидание случайной величины Y=2X+2, если математическое ожидание X равно 3?

Чему равно математическое ожидание случайной величины Y=2X-2, если математическое ожидание X равно 4?

Чему равно математическое ожидание случайной величины Y=2X-2, если математическое ожидание X равно 5?

Чему равно математическое ожидание случайной величины Y=4X+2, если математическое ожидание X равно 3?

Чему равно математическое ожидание постоянной величины?

Ответ: этой величине

Чему равно математическое ожидание произведения независимых случайных величин?

Ответ: произведению их математических ожиданий

Чему равно математическое ожидание суммы случайных величин?

Ответ: сумме их математических ожиданий

Что называют мощностью критерия 1-β?

Ответ: Нулевая гипотеза не верна и ее отвергают согласно критерию

Что называют мощностью критерия1-β?

Ответ: вероятность не допустить ошибку второго рода

Ответ: Нулевая гипотеза не верна, но ее принимают согласно критерию

Что называют ошибкой первого рода α?

Ответ: Нулевая гипотеза верна, но ее отвергают согласно критерию

Что показывает множественный коэффициент корреляции?

Ответ: тесноту связи между одной величиной и совместным действием остальных величин

Что показывает парный коэффициент корреляции?

Ответ: тесноту связи между величинами X и Y на фоне действия остальных переменных

Что показывает частный коэффициент корреляции?

Ответ: тесноту связи между двумя переменными при фиксированном значении остальных

Что является несмещѐнной точечной оценкой генеральной дисперсии?

Ответ: исправленная выборочная дисперсия

Что является точечной оценкой генеральной дисперсии?

Ответ: выборочная дисперсия

Что является точечной оценкой генеральной доли или вероятности p?

Ответ: частость (относительная частота) события

Что является точечной оценкой математического ожидания?

Ответ: средняя арифметическая

Что является центром при построении доверительного интервала для генеральной доли или вероятности?

Ответ: частость (относительная частота) события

Что является центром при построении доверительного интервала для генеральной средней?

Ответ: средняя арифметическая

Ширина доверительного интервала при построении интервальных оценок зависит от:

Ответ: доверительной вероятности (надѐжности) и числа наблюдений

Источник

Оценка генеральной доли

Пусть требуется оценить долю тех объектов заданной генеральной совокупности, которые удовлетворяют некоторому условию – генеральную долю . Для этого из генеральной совокупности выделяют выборку, и по результатам её обследования находят долю тех объектов, которые удовлетворяют условию – выборочную долю . Очевидно, что , где – объем выборки, – число тех её объектов, которые удовлетворяют условию . Выборочная доля в данном случае является той величиной, с помощью которой мы получим информацию о неизвестном значении генеральной доли.

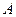
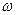
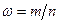
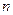
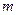
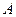
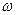
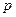
Таким образом, выборочная доля является оценкой генеральной доли .

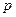
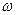
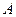
Пример. – доля бракованных деталей генеральной совокупности, – доля бракованных деталей в выборке. Условие (событие) – деталь, взятая наудачу из генеральной совокупности – бракована.

Простейший способ оценивания – точечное оценивание – подразумевает использование приближенного равенства .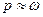

Как и всякая оценка, выборочная доля 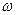является случайной величиной. Действительно, выборка из генеральной совокупности выделяется случайным образом. Соответственно то значение, которое примет выборочная доля, будет случайным.

Следующие теоремы характеризуют выборочную долю как случайную величину.

Теорема 1.Математическое ожидание выборочной доли равно генеральной доле:

.

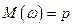
Среднее квадратическое отклонение () выборочной доли вычисляется по формулам

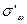
– в случае повторной выборки и

– в случае бесповторной выборки, где 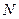– объем генеральной совокупности.

Напомним, что по определению среднего квадратического отклонения в случае повторной выборки имеем 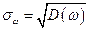(аналогично в случае бесповторной выборки).

Замечание. При применении формул Теоремы 1 полагают

.

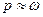
Теорема 2.Закон распределения выборочной доли неограниченно приближается к нормальному закону при неограниченном увеличении объема выборки.

Подобно тому, как мы это сделали в предыдущем параграфе, как следствие Теоремы 2, получаем формулу доверительной вероятности:

– в случае повторной выборки. Заменяя в последнем равенстве на , получаем формулу доверительной вероятности в случае бесповторной выборки.

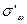
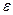
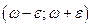
По определению, величина , фигурирующая в формуле доверительной вероятности, называется предельной ошибкой выборки. Интервал называется доверительным интервалом.

Выше было указано, в чем состоит точечная оценка генеральной доли. Интервальное оценивание сводится, например, к вычислению значения доверительной вероятности при заданной предельной ошибке выборки.

Теорема 3.В случае повторной выборки выборочная доля является несмещенной и состоятельной оценкой генеральной доли.

Пример.Выборочные данные о надое молока для 100 коров из 1000 представлены таблицей:

Надой молока, ц	10-20	20-30	30-40	40-50	50-60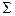
Число коров

1. Найти вероятность того, что доля всех коров с надоем молока более 40 ц отличается от такой доли в выборке не более чем на 0,05 (по абсолютной величине), для случая повторной и бесповторной выборок.

2. Найти границы, в которых с вероятностью 0,9596 заключена доля всех коров с надоем более 40 ц.

3. Сколько коров надо обследовать, чтобы с вероятностью 0,9786 для генеральной доли коров с надоем более 40 ц можно было гарантировать те же границы что и в п.2.

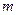
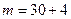
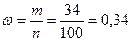
Решение. Число коров с надоем более 40 ц равно 34 (, см. заданный вариационный ряд). Тогда .

Для нахождения доверительной вероятности п. 1 задания воспользуемся одноименной формулой при .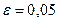

Пусть рассматриваемая выборка – повторная. Тогда по формуле Теоремы 1, учитывая Замечание, получаем

.

.

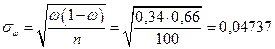
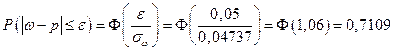
Аналогично, в случае бесповторной выборки:

,

.

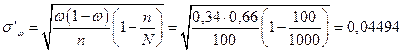
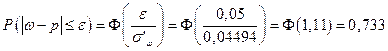
Доверительным в данном случае является интервал 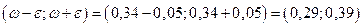. Таким образом, неизвестное значение доли всех коров с надоем более 40 ц накрывается доверительным интервалом (0,29;0,39) с вероятностью 0,7109 в случае повторной выборки и с вероятностью 0,733 в случае бесповторной выборки.

В п. 2 задания при заданном значении доверительной вероятности искомым является доверительный интервал. Поскольку значение выборочной доли известно, остается найти предельную ошибку выборки .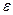

Пусть выборка – повторная. По условию, принимая во внимание формулу доверительной вероятности, имеем

.

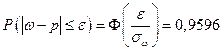
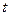
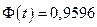
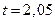
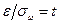
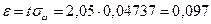
По таблице значений функции Лапласа найдем такое , что : . Тогда и, используя найденное выше значение , получаем

.

Соответственно, доверительным будет интервал:

.

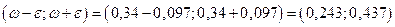
Пусть выборка – бесповторная. Аналогично предыдущему, получаем предельную ошибку выборки

и доверительный интервал:

.

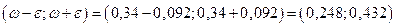
Таким образом, доля всех коров с надоем молока более 40 ц с вероятностью 0,9596 накрывается доверительным интервалом (0,243; 0,437) в случае повторной выборки и интервалом (0,248; 0,432) в случае бесповторной выборки.

В п. 3 по заданным значениям доверительной вероятности и предельной ошибки выборки найдем необходимый объем выборки. Из начла решения заимствуем значение выборочной доли 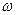, найденное по исходному вариационному ряду.

Пусть выборка – повторная. По условию, принимая во внимание формулу доверительной вероятности, имеем:

.

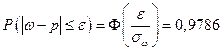
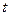
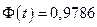
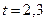
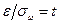
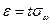
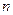
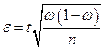
По таблице значений функции Лапласа найдем такое , что : . Тогда и, . Подставляя вместо выражение из Теоремы 1, приходим к уравнению относительно неизвестной величины :

.

Решая это уравнение относительно 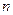, подставляя в полученную формулу известные величины, завершаем решение

(заметим, что, как и ранее, округление здесь произведено в большую сторону).

Аналогично, в случае бесповторной выборки из условия и формулы доверительной вероятности следует равенство

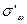
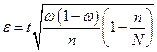
или, принимая во внимание известное выражение для (см. Теорему 1):

.

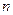
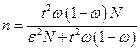
Решая это уравнение относительно , получаем

.

Подставляя в правую часть последнего равенства известные значения, окончательно имеем:

.

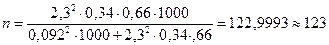
Таким образом, в повторную выборку надо взять 127 коров, чтобы с вероятностью 0,9786 можно было утверждать, что доля всех коров с надоем молока более 40 ц накрывается доверительным интервалом (0,243; 0,437). Аналогично, в бесповторную выборку надо взять 123 коровы, чтобы с вероятностью 0,9786 можно было утверждать, что доля всех коров с надоем молока более 40 ц накрывается доверительным интервалом (0,248; 0,432).

Домашнее задание:9.19, 9.21, 9.23, 9.30.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Оценки параметров генеральной совокупности. Доверительные интервалы

п.1. Переход от выборки к генеральной совокупности

50 посетителей магазина, заполнившие анкеты

Все будущие посетители магазина

100 опрошенных школьников

Все школьники города/области/страны

10 опытов с определением периода математического маятника

Все математические маятники

Насколько большой должна быть выборка, чтобы надежно представлять генеральную совокупность? К концу параграфа мы получим ответ на этот вопрос для определенного класса задач.

Попутно заметим, что малой называют выборку, если при исследовании одного признака её объем \(n\lt 30\), а при исследовании k признаков \(\frac\lt 10\).

п.2. Способы, виды и методы отбора

Пять способов отбора

п.3. Распространение результатов выборки на генеральную совокупность при изучении альтернативного признака

Например:
1) орел или решка;
2) 0 или 1;
3) качественный или бракованный и т.п.

Мы уже знаем, что конечное число экспериментов с таким признаком описывается биномиальным распределением (см. §40 справочника для 9 класса), а при \(n\rightarrow \infty\) биномиальное распределение приближается к нормальному (см. §64 данного справочника).

При исследовании альтернативного признака x генеральной совокупности с помощью выборки будем использовать следующие обозначения:

Например:
Из партии товара в 1000 изделий было случайным образом выбрано 100 изделий, и среди них обнаружено 8 бракованных. Для этой выборки можем записать: \begin N=1000,\ n=100,\ n_x=8,\ w=\frac<8><100>=0,08\\ \sigma^2=w(1-w)=\frac<8><100>\cdot\frac<92><100>=\frac<736><10000>=0,0736;\ \ \sigma=\sqrt<\frac<736><10000>>\approx 0,2713 \end

Доверительным интервалом оценки неизвестного параметра генеральной совокупности называют вычисленный на основе данных выборки интервал, в котором генеральный параметр содержится с известной вероятностью.

п.4. Минимальный объем выборки

п.4. Алгоритм построения доверительного интервала для оценки генеральной доли

Повторная выборка
На входе: объем выборки n, число повторений признака \(n_x\), доверительная вероятность \(P\)
Шаг 1. Найти выборочную долю \(w=\frac\), дисперсию \(\sigma=\sqrt\)
Шаг 2. Найти среднюю ошибку выборки \(m=\frac<\sigma><\sqrt>\)
Шаг 3. Найти уровень значимости \(\alpha=1-P\), рассчитать \(Z_\alpha\) (если в Excel, то НОРМСТОБР(1-α/2))
Шаг 4. Найти предельную ошибку выборки \(\triangle =Z_\alpha m\)
На выходе: интервал для генеральной доли \(p=w\pm\triangle\)

Бесповторная выборка
На входе: объем генеральной совокупности N, объем выборки n, число повторений признака \(n_x\), доверительная вероятность \(P\)
Шаг 1. Найти выборочную долю \(w=\frac\), дисперсию \(\sigma=\sqrt\)
Шаг 2. Найти среднюю ошибку выборки \(m=\frac<\sigma><\sqrt>\sqrt<1-\frac nN>\)
Шаг 3. Найти уровень значимости \(\alpha=1-P\), рассчитать \(Z_\alpha\) (если в Excel, то НОРМСТОБР(1-α/2))
Шаг 4. Найти предельную ошибку выборки \(\triangle =Z_\alpha m\)
На выходе: интервал для генеральной доли \(p=w\pm\triangle\)

п.5. Для каких величин строят доверительные интервалы?

В этом параграфе мы научились строить доверительный интервал для оценки биномиальной доли в генеральной совокупности.

На практике в статистических исследованиях доверительные интервалы строят для:
— оценки математического ожидания в генеральной совокупности, если выборка образует вариационный ряд (дискретный или непрерывный). Здесь разделяют два случая: а) генеральная дисперсия известна или б) она неизвестна;
— оценки дисперсии генеральной совокупности, если выборка образует вариационный ряд (дискретный или непрерывный). Здесь также разделяют два случая: а) генеральная средняя известна или б) она неизвестна.

Подробней о построении различных доверительных интервалов вы можете узнать из вузовских курсов теории вероятностей и статистики.

п.6. Примеры

Пример 1. Перед выборами мера в городе был проведен опрос 1000 человек (2% бесповторная выборка). В результате опроса оказалось, что за кандидата Y готовы проголосовать 423 человека из опрошенных. Определите с уровнем значимости 3% долю сторонников кандидата Y в городе.

Пример 2. Какое минимальное число людей нужно опросить в городе из предыдущего примера, чтобы можно было с уровнем значимости 3% получить предельную ошибку для генеральной доли \(\triangle=\)1%. Выборка бесповторная.

Источник