Что является разверткой цилиндра
Инструменты пользователя
Инструменты сайта
Боковая панель
Стереометрия:
Контакты
Цилиндр
Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.
Вот другое определение:
Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.
Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.
Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.
Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.
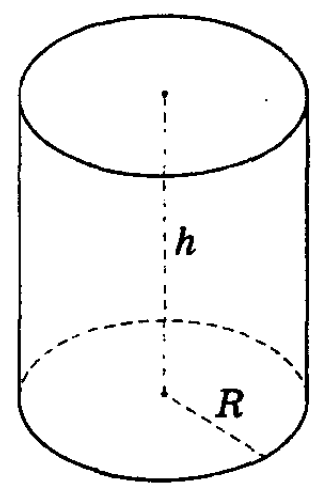
Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.
Круговой цилиндр — цилиндр, основания которого являются кругами.
Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.
Радиус цилиндра – радиус его основания.
Образующая цилиндра — образующая цилиндрической поверхности.
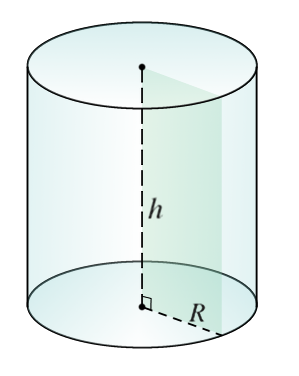
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.
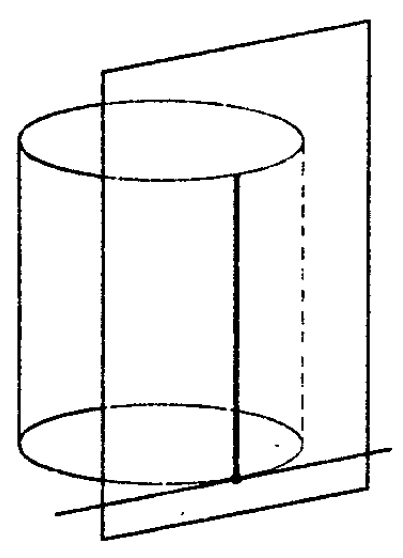
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.
Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.
Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класса
Урок №6. Тела вращения. Цилиндр
Перечень вопросов, рассматриваемых в теме:
Цилиндрическая поверхность – это поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность.
Эти прямые – образующие цилиндрической поверхности.
Прямая, проходящая через центр окружности, перпендикулярно к плоскости – ось цилиндрической поверхности.
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами.
Круги – основания цилиндра; отрезки образующих, заключённые между основаниями – образующие цилиндра; образованная ими часть цилиндрической поверхности – боковая поверхность.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Сечение – изображение фигуры, образованной рассечением тела плоскостью.
Осевое сечение – вариант сечения, при котором плоскость проходит через ось тела.
Развёртка боковой поверхности цилиндра – прямоугольник, одна сторона которого равна высоте цилиндра, а другая длине окружности основания.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций: базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс.
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-79.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Основные определения
Цилиндрической поверхностью называется поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность (см.рис.).
Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.
Так как все образующие и ось перпендикулярны плоскости 𝛂, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).
Если построить ещё одну плоскость 𝛃, которая будет параллельна плоскости 𝛂, то отрезки образующих, заключённые между плоскостями 𝛂 и 𝛃 будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости 𝛃, дают окружность, равную окружности, лежащей в плоскости 𝛂.
Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях 𝛂 и 𝛃) называется цилиндром.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.
Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.
2. Сечения цилиндра различными плоскостями
Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.
Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).
3. Основные формулы
Формула для вычисления площади боковой поверхности цилиндра: Sбок=2𝛑RL.
То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2𝛑R(R+L).
Примеры и разбор решения заданий тренировочного модуля
Выберите значение площади его боковой поверхности
Площадь боковой поверхности вычисляется по формуле: S=2πRL.
Найдем сторону АВ сечения.
НВ=ОН·tg60 0 =1·
Sсеч=6

3. Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.
По условию задачи L=R+6.
Получили квадратное уравнение относительно радиуса:
R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Развертка прямого кругового цилиндра.
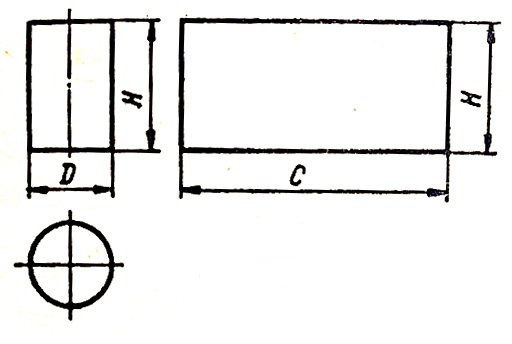
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.
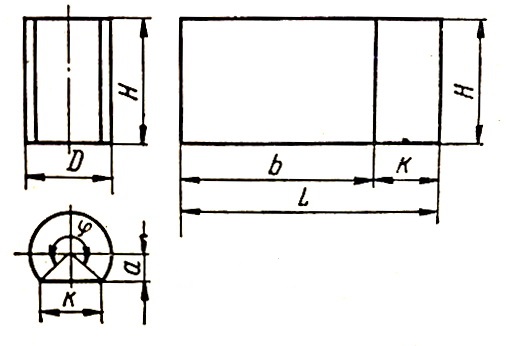
Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2) 2 – a 2 ) = 2a tg (ᵠ/2).
Рис. 1.
Рис. 2.
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
Рис. 3.
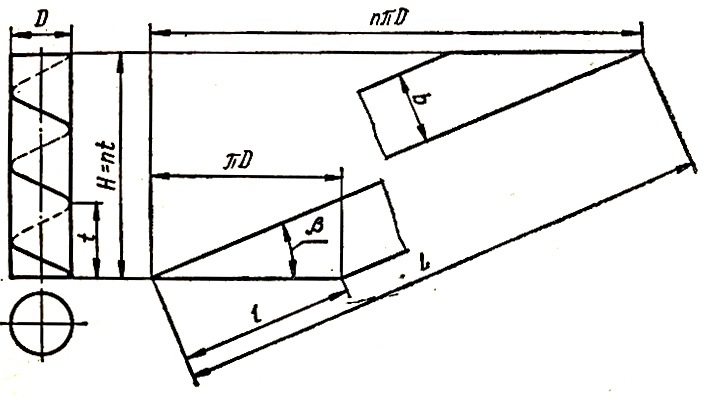
Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:
D — диаметр цилиндра;
t — шаг винтовой линии;
n — число полных витков на общей длине цилиндра H, Н = nt;
L — общая длина ленты;
Развертка усеченного цилиндра.
Цилиндр показан на рис. 4.
Рис. 4.
Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′1, 1′1…, 6′1. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 00, 10, …, 60 строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 0 0 1, 1 0 1, …, 6 0 1. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.
Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′13′1 и b = D/2.
Рис. 5.
При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:
xk = kx1 = πD/2 kε/180°; yk = D/2 tg α sin kε = A sin kε = A sin ᵠi,
где х1 = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠi= kε.
Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.
Таблица 1. Значения sin kε и sin 2 kε
| 2n | sin kε | sin 2 kε | 2n | sin kε | sin 2 kε | ||||||
| 8 | 16 | 32 | 64 | 12 | 24 | 48 | 96 | ||||
| — | — | — | 1 | 0,09802 | 0,00961 | — | — | — | 1 | 0,06540 | 0,00428 |
| — | — | 1 | 2 | 0,19509 | 0,03806 | — | — | 1 | 2 | 0,13053 | 0,01704 |
| — | — | — | 3 | 0,29028 | 0,08426 | — | — | — | 3 | 0,19509 | 0,03806 |
| — | 1 | 2 | 4 | 0,38268 | 0,14645 | — | 1 | 2 | 4 | 0,25882 | 0,06699 |
| — | — | — | 5 | 0,47139 | 0,22221 | — | — | — | 5 | 0,32144 | 0,10332 |
| — | — | 3 | 6 | 0,55557 | 0,30866 | — | — | 3 | 6 | 0,38268 | 0,14645 |
| — | — | — | 7 | 0,63439 | 0,40245 | — | — | — | 7 | 0,44229 | 0,19562 |
| 1 | 2 | 4 | 8 | 0,70711 | 0,50000 | 1 | 2 | 4 | 8 | 0,50000 | 0,25000 |
| — | — | — | 9 | 0,77301 | 0,59754 | — | — | — | 9 | 0,55557 | 0,30866 |
| — | — | 5 | 10 | 0,83147 | 0,69134 | — | — | 5 | 10 | 0,60876 | 0,37059 |
| — | — | — | 11 | 0,88192 | 0,77778 | — | — | — | 11 | 0,65935 | 0,43474 |
| — | 3 | 6 | 12 | 0,92388 | 0,85355 | — | 3 | 6 | 12 | 0,70711 | 0,50000 |
| — | — | — | 13 | 0,95694 | 0,91573 | — | — | — | 13 | 0,75184 | 0,56526 |
| — | — | 7 | 14 | 0,98079 | 0,96194 | — | — | 7 | 14 | 0,79335 | 0,62941 |
| — | — | — | 15 | 0,99518 | 0,99039 | — | — | — | 15 | 0,83147 | 0,69134 |
| 2 | 4 | 8 | 16 | 1,00000 | 1,00000 | 2 | 4 | 8 | 16 | 0,86617 | 0,75000 |
| — | — | — | 17 | 0,89687 | 0,80438 | ||||||
| — | — | 9 | 18 | 0,92388 | 0,85355 | ||||||
| — | — | — | 19 | 0,94693 | 0,89668 | ||||||
| — | 5 | 10 | 20 | 0,96600 | 0,93301 | ||||||
| — | — | — | 21 | 0,98079 | 0,96194 | ||||||
| — | — | 11 | 22 | 0,99144 | 0,98296 | ||||||
| — | — | — | 23 | 0,99786 | 0,99572 | ||||||
| 3 | 6 | 12 | 24 | 1,00000 | 1,00000 | ||||||
Примечание: Значения sin kε и sin 2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.
Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у0 до у3. Остальные координаты имеют соответственно равные значения. Например: у4 — у2, …, у11 = — у1 и т. д.