Что является самым большим числом в мире
10 самых больших и важных чисел
Дети часто задают вопрос: «Какое число самое большое?». Этот вопрос — важный шаг в процессе перехода в мир абстрактных понятий. Ответ, конечно, прост: числа, скорее всего, бесконечны, но есть определенный порог, за которым числа становятся настолько большими, что в них нет смысла, кроме того, что технически они могут существовать. Давайте возьмем десятку гигантских чисел, известных нам, но ограничимся крайне важными понятиями в мире чисел.
Десять в восьмидесятой степени — 1 с 80 нулями — это довольно массивное число, обозначающее примерное число элементарных частиц в известной вселенной, и, говоря элементарные частицы, мы не имеем в виду микроскопические частицы — мы говорим о куда меньших вещах вроде кварков и лептонов — о субатомных частицах. Это число в США и современной Великобритании называют «сто квинквавигинтиллионов». Вроде бы, несложно понять, что это число обозначает количество мельчайших частиц в нашей Вселенной, однако это самое маленькое и простое число в нашем списке.
Один гугол
Слово гугол, несколько измененное, стало часто используемым в современности, благодаря популярной поисковой системе. У этого числа есть интересная история — достаточно просто погуглить. Термин был придуман Милтоном Сироттой в 1938 году, когда ему было 9 лет. И хотя это относительно абстрактное число, и его существование объясняется необходимостью технического существования, ему все-таки нашли применение.
Алексис Лемер поставил мировой рекорд, рассчитав корень тринадцати из стозначного числа. Гугол — это стозначное число, число с сотней нулей. Также предполагается, что от одного до полутора гугол лет с момента Большого Взрыва взорвется самая массивная черная дыра. И тогда Вселенная вступит в так называемую «темную эпоху» — конец той научной вселенной, какой мы ее знаем.
8,5 х 10^185
Длина Планка — это очень маленькая длина, примерно 1,616199 x 10-35, или 0,00000000000000000000000000000616199 метра. В дюймовом кубе этих длин примерно с гугол. Длина и объем Планка играют важную роль в отраслях квантовой физике — например, теории струн — поскольку позволяют производить вычисления на самых мельчайших масштабах. Во вселенной примерно 8,5 x 10^185 объемов Планка. Это достаточно большое число, и ему все же нет практического применения, но оно остается достаточно простым в нашем списке.
2^43,112,609 – 1
Третье по величине число в этом списке — это число всех планковых объемов во Вселенной, и в нем 185 цифр. А в этом числе почти 13 миллионов цифр. Чем это число важно? Это самое большое из известных сегодня простых чисел. Его обнаружили в августе 2008 года в ходе Great Internet Messene Prime Search (GIMPS).
Гуголплекс
Вы наверняка слышали это слово, хотя бы в фильме «Назад в будущее», когда доктор Эммет Браун бормотал «она одна на миллион, одна на миллиард, одна на гуголплекс». Что такое гуголплекс? Помните длину гугола? Единица и сто нулей. А гуголплекс — это десять в степени гугол. Это больше, чем число всех частиц в известной нам части вселенной.
Вы можете отметить, что можно возводить десять в степень гуголплекс и будет еще больше, и так далее, и окажетесь совершенно правы.
Числа Скьюза
Число Скьюза — это верхний предел для математической задачи π(x) > Li(x), хоть и просто выглядящей, но крайне сложной на самом деле. По существу, число Скьюза доказывает, что число x существует и нарушает это правило, если предположить, что гипотеза Римана верна, а число x меньше, чем 10^10^10^36, первое число Скьюза. Даже первое число Скьюза больше гуголплекса. Есть также и самое большое число Скьюза: x меньше, чем 10^10^10^963.
Время возвращения Пуанкаре
Это очень сложная вещь, но основная концепция относительно проста: при наличии достаточного времени, все возможно. Теорема Пуанкаре о возвращении предполагает количество времени, которого было бы достаточно для того, чтобы однажды вся Вселенная вернулась в свое нынешнее состояние, вызванное случайными квантовыми флуктуациями. Короче, «история повторится». Предполагается, что это займет 10^10^10^10^10^1,1 лет.
Число Грэма
В 80-х годах это число попало в Книгу рекордов Гиннесса как самое массивное конечное число, когда-либо использованное в математических доказательствах. Оно было выведено Роном Грэмом как верхний предел для проблем теории Рамси о многоцветных гиперкубах. Число настолько большое, что для его записи используется стрелочная нотация Кнута (метод записи больших чисел) и собственное уравнение Грэма. Метод Кнута и принцип работы стрелок сложно объяснить, но вы можете представить себе это так. 3↑3 превращается в 3^3 или 27, 3↑↑3 превращается в 3^3^3 или 7,625,597,484,987. Вы можете добавить еще одну стрелку к 3↑↑↑3 и выйти на 7,5 триллионов уровней. Само по себе это число значительно больше, чем время возвращения Пуанкаре, поскольку вы можете добавить бесконечное число стрелок, и каждая стрелка будет невероятно увеличивать число.
Число Грэма выглядит так: G=f64(4), где f(n)=3↑^n3. Лучший способ его представить — разложить по полочкам. Первый слой — это 3↑↑↑↑3, что уже невероятно много. Следующий слой — это множество стрелок между тройками. Возьмите эти стрелки и поместите между следующими тройками. Это умножается в 64 раза. Даже сам Грэм не знает первое число, но последние десять вот: 2464195387. Вся наблюдаемая вселенная слишком мала, чтобы вместить в себя обыкновенную десятичную запись числа Грэма.
∞. Бесконечность
Это число известно всем и каждому, оно часто используется для преувеличений — как какой-нибудь «многоллион». Однако это число намного сложнее, чем большинство может представить, и если вы могли представить числа, идущие до этого пункта, именно это число очень странное и противоречивое. Согласно правилам бесконечности, есть бесконечное число нечетных и четных чисел в бесконечности, однако только половина от всех чисел может быть четной. Бесконечность плюс один равна бесконечности, бесконечность минус один равна бесконечности, бесконечность плюс бесконечность равна бесконечности, деленная пополам — тоже бесконечность, бесконечность минус бесконечность — никто не знает, бесконечность, деленная на бесконечность, будет, скорее всего, 1.
Ученые полагают, что в известной вселенной около 10^80 субатомных частиц, но это только известная вселенная. Некоторые предполагают, что вселенная бесконечна. Если это так, то математически достоверно, что есть другая Земля где-то там, где каждый атом складывается таким же образом, как и мы, и наша Земля. Шанс того, что копия Земли существует, невероятно мал, но в бесконечной вселенной это не только может произойти, но и бесконечно много раз.
В бесконечность верят не все. Израильский профессор математики Дорон Зильбергер утверждает, что по его мнению, числа не будут продолжаться вечно, и найдется настолько большое число, что когда вы добавите к нему единицу, вы придете к нулю. И хотя это число едва ли когда будет обнаружено и едва ли кто сможет его вообразить, бесконечность является важной частью математической философии.
Самое большое число в мире
Считается, что концепция чисел впервые возникла, когда доисторические люди начали использовать свои пальцы для подсчета чего-либо. С тех пор человечество прошло долгий путь. Теперь мы используем калькуляторы и компьютеры для подсчета самых больших чисел. И даже появились названия для чисел, которые настолько велики, что их с трудом можно представить.
Бесконечность счетных чисел
Казалось бы, ответ на вопрос о том, каково самое большое число в математике — очень прост. Бесконечность, верно? Но это не совсем правильно. Ведь бесконечность — вовсе не число, а концепция. Идея.
Бесконечность (infinitum) — это понятие, которое в переводе с латинского означает «без границ». Определение бесконечности в математике гласит, что независимо от того, насколько велико число, вы всегда можете добавить к нему 1, и оно станет больше.
Поэтому, строго говоря, не существует такого понятия, как самое большое число в мире. Можно лишь назвать наибольшее число, которому дали конкретное название.
Вот некоторые наиболее известные названия больших чисел:
| Число нулей | Название | Название на английском |
|---|---|---|
| 3 | тясяча | thousand |
| 6 | миллион | million |
| 9 | миллиард (биллион) | billion |
| 12 | триллион | trillion |
| 15 | квадриллион | quadrillion |
| 18 | квинтиллион | quintillion |
| 21 | секстиллион | sextillion |
| 24 | септиллион | septillion |
| 27 | октиллион | octillion |
| 30 | нониллион | nonillion |
| 33 | дециллион | decillion |
| 36 | ундециллион | undecillion |
| 39 | дуодециллион | duodecillion |
| 42 | тредециллион | tredecillion |
| 45 | кватуордециллион | quattuordecillion |
| 48 | квиндециллион | quindecillion |
| 51 | сексдециллион | sexdecillion |
| 54 | септендециллион | septendecillion |
| 57 | октодециллион | octodecillion |
| 60 | новемдециллион | novemdecillion |
| 63 | вигинтиллион | vigintillion |
| 66 | унвигинтиллион | unvigintillion |
| 69 | дуовигинтиллион | duovigintillion |
| 72 | тревигинтиллион | trevigintillion |
| 75 | кватуорвигинтиллион | quattuorvigintillion |
| 78 | квинвигинтиллион | quinvigintillion |
| 81 | сексвигинтиллион | sexvigintillion |
| 84 | септенвигинтиллион | septenvigintillion |
| 87 | октовигинтиллион | octovigintillion |
| 90 | новемвигинтиллион | novemvigintillion |
| 93 | тригинтиллион | trigintillion |
| 96 | унтригинтиллион | untrigintillion |
| 99 | дуотригинтиллион | duotrigintillion |
| 102 | третригинтиллион | trestrigintillion |
| 105 | кватортригинтиллион | quattuortrigintillion |
| 108 | квинтригинтиллион | quintrigintillion |
| 111 | секстригинтиллион | sextrigintillion |
| 114 | септентригинтиллион | septentrigintillion |
| 117 | октотригинтиллион | octotrigintillion |
| 120 | новемтригинтиллион | novemtrigintillion |
| 123 | квадрагинтиллион | quadragintillion |
| 126 | унквадрагинтиллион | unquadragintillion |
| 129 | дуоквадрагинтиллион | duoquadragintillion |
| 132 | треквадрагинтиллион | trequadragintillion |
| 135 | кваторквадрагинтиллион | quattuorquadragintillion |
| 138 | квинквадрагинтиллион | quinquadragintillion |
| 141 | сексквадрагинтиллион | sexquadragintillion |
| 144 | септенквадрагинтиллион | septenquadragintillion |
| 147 | октоквадрагинтиллион | octoquadragintillion |
| 150 | новемквадрагинтиллион | novemquadragintillion |
| 153 | квинквагинтиллион | quinquagintillion |
| 156 | унквинкагинтиллион | unquinquagintillion |
| 159 | дуоквинкагинтиллион | duoquinquagintillion |
| 162 | треквинкагинтиллион | trequinquagintillion |
| 165 | кваторквинкагинтиллион | quattuorquinquagintillion |
| 168 | квинквинкагинтиллион | quinquinquagintillion |
| 171 | сексквинкагинтиллион | sexquinquagintillion |
| 174 | септенквинкагинтиллион | septenquinquagintillion |
| 177 | октоквинкагинтиллион | octoquinquagintillion |
| 180 | новемквинкагинтиллион | novemquinquagintillion |
| 183 | сексагинтиллион | sexagintillion |
| 186 | унсексагинтиллион | unsexagintillion |
| 189 | дуосексагинтиллион | duosexagintillion |
| 192 | тресексагинтиллион | tresexagintillion |
| 195 | кваторсексагинтиллион | quattuorsexagintillion |
| 198 | квинсексагинтиллион | quinsexagintillion |
| 201 | секссексагинтиллион | sexsexagintillion |
| 204 | септенсексагинтиллион | septensexagintillion |
| 207 | октосексагинтиллион | octosexagintillion |
| 210 | новемсексагинтиллион | novemsexagintillion |
| 213 | септагинтиллион | septuagintillion |
| 216 | унсептагинтиллион | unseptuagintillion |
| 219 | дуосептагинтиллион | duoseptuagintillion |
| 222 | тресептагинтиллион | treseptuagintillion |
| 225 | кваторсептагинтиллион | quattuorseptuagintillion |
| 228 | квинсептагинтиллион | quinseptuagintillion |
| 231 | секссептагинтиллион | sexseptuagintillion |
| 234 | септенсептагинтиллион | septenseptuagintillion |
| 237 | октосептагинтиллион | octoseptuagintillion |
| 240 | новемсептагинтиллион | novemseptuagintillion |
| 243 | октогинтиллион | octogintillion |
| 246 | уноктогинтиллион | unoctogintillion |
| 249 | дуооктогинтиллион | duooctogintillion |
| 252 | треоктогинтиллион | treoctogintillion |
| 255 | кватороктогинтиллион | quattuoroctogintillion |
| 258 | квиноктогинтиллион | quinoctogintillion |
| 261 | сексоктогинтиллион | sexoctogintillion |
| 264 | септоктогинтиллион | septoctogintillion |
| 267 | октооктогинтиллион | octooctogintillion |
| 270 | новемоктогинтиллион | novemoctogintillion |
| 273 | нонагинтиллион | nonagintillion |
| 276 | уннонагинтиллион | unnonagintillion |
| 279 | дуононагинтиллион | duononagintillion |
| 282 | тренонагинтиллион | trenonagintillion |
| 285 | кваторнонагинтиллион | quattuornonagintillion |
| 288 | квиннонагинтиллион | quinnonagintillion |
| 291 | секснонагинтиллион | sexnonagintillion |
| 294 | септеннонагинтиллион | septennonagintillion |
| 297 | октононагинтиллион | octononagintillion |
| 300 | новемнонагинтиллион | novemnonagintillion |
| 303 | центиллион | centillion |
Как называется самое большое простое число

Какое самое большое число в мире

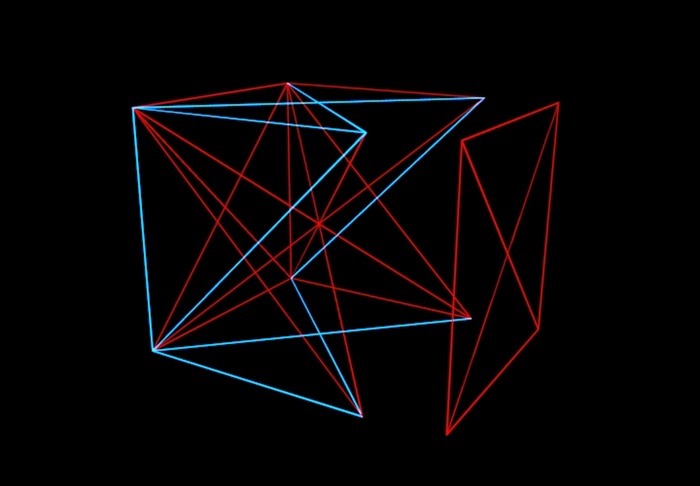
Кратко об этой теории: представим себе N-мерный куб, его вершины в случайном порядке соединены красными или синими отрезками-линиями. А наша задача — понять, до какого значения N возможно (если по-разному закрашивать ребра куба), избежать ситуации, при которой одна плоскость в кубе будет окрашена одним цветом. То есть у нас не должен получиться одноцветный «конвертик».
Математики позакрашивали кубик и так и эдак, получилось, что до шестимерного куба можно исхитриться и сделать, чтобы линии одного цвета, соединяющие четыре вершины, не лежали в одной плоскости. А вот с семимерным, как выяснили Грэм и Ротшильд, такой фокус уже не провернешь. И с восьмимерным. И… «и так далее», которое, впрочем, не бесконечно, а заканчивается фантастически гигантским числом. Вот его-то и именуют числом Грэма. Кстати, в настоящее время решение Грэма и Ротшильда устарело. Математики выяснили, что 6-7-8-9-10-11-12-мерные кубы все же можно покрасить без «конвертов». Но где-то в промежутке между 13 и числом Грэма гарантированно есть число выше которого «конверты» в любом случае будут.
Число Грэма получило всемирное признание в 1977 году, когда известный популяризатор науки Мартин Гарднер написал об этом в Scientific American.
И хотя с тех пор в математической науке были и другие кандидаты на титул самого большого числа, «детище» Грэма является самым распиаренным и общеизвестным. И если вы слышали про «гугольное семейство»:
Любопытно, что придумав гугол американский математик Эдвард Казнер хотел показать студентам разницу между невероятно большим числом и бесконечностью. Тогда число Грэма может просто «взорвать мозг».
Возможно ли представить и записать число за гранью понимания
Математики не смогут назвать вам точное количество цифр в числе Грэма, не говоря уже о том, чтобы досчитать до него. Известны лишь последние 50 цифр самого большого числа в мире — это …03222348723967018485186439059104575627262464195387.
А вот цифры, с которых начинается G64 неизвестны, и вряд ли когда-либо будут.
Давайте сравним трех монстров: гугол, гуголплекс и число Грэма.
Теперь представьте, что в какой-то момент вы берете одну песчинку, чтобы рассмотреть ее под мощным микроскопом. И видите, что на самом деле это не единственное зерно, а 10 миллиардов микроскопических зерен, а все вместе они размером с песчинку. Если бы это было так для каждой отдельной песчинки в этой гипотетической вселенной, то общее количество этих микроскопических зерен было бы гуголом.
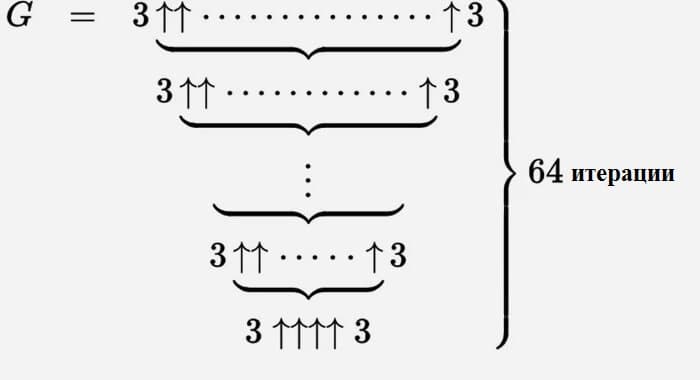
Как записать G64 с помощью метода Кнута
В 1976 году американский ученый Дональд Кнут предложил понятие сверхстепеней или нотацию Кнута. Это метод, позволяющий при помощи стрелочек, направленных вверх, записывать очень большие числа. Возведение в степень обозначается одной стрелкой вверх: ↑.
Вот как выглядит эта нотация: a ↑ b = ab = a × a × a × …, и так b раз.
Важной особенностью стрелок вверх является то, что они растут очень быстро. Экспонентация растет гораздо быстрее, чем умножение. 2 × 10 — это всего лишь 20, но 2↑10 = 1024. Таким же образом, каждый новый уровень стрелок растет намного быстрее, чем предыдущий уровень.
Если мысленно представить себе степенную башню из троек 3↑↑↑4 то получится конструкция, размером от Земли до Марса. А ведь мы еще даже не дошли до «нижней ступеньки», ведущей нас к числу Грэма.
Мы можем описать число Грэма огромным набором этих стрелок вверх.
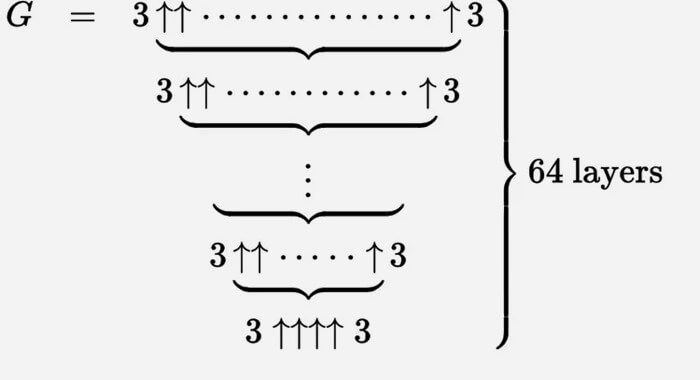
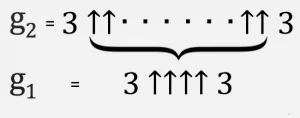
Проще всего думать об этом как об итерационном процессе. Мы начинаем снизу с g 1 = 3 ↑↑↑↑ 3, а затем создаем вторую строку (назовем ее g 2) с g 1 стрелками между тройками.
Тогда g 3 — это две тройки, разделенные g 2 стрелками вверх и так далее, пока g 64 с g 63 стрелками между тройками не будет числом Грэма.
Если выбрать продолжительность жизни, равную числу Грэма вместо бессмертия, то результат будет практически одинаков. Даже если предположить, что условия во Вселенной, в Солнечной системе и на Земле вечно останутся неизменными, человеческий мозг никак не мог бы выдержать столь длинный промежуток времени без пагубных изменений.
Самое большое число
Продолжительное время пользовался популярностью слух о том, что престижнейшую в мире премию не присуждают математикам исключительно потому, что Альфред Нобель некогда из-за представителя «братства цифр и формул» пережил неприятный казус — якобы супруга «взрывного» предпринимателя с помощью упомянутого милого человека снабдила мужа развесистыми рогами.
Люди, привыкшие в меньшей мере доверять фантазии и слухам, предполагают: причина в том, что в математике, как науке прикладной, никаких свершений уже не будет — все открыто, и прорыва ждать не приходится. Но в пику мертвому Нобелю «адепты логарифмов» продолжают пытаться доказать, что математика — это не только инструмент для вычислений, а нечто большее, и продолжают находить и изучать новые аспекты любимой науки, стремясь, например, отыскать самое большое число — о чем и пойдет речь ниже.
Невозможное возможно, если сильно захотеть
Возможно, некоторые люди неоднократно задавались вопросом о том, есть ли самое большое число, после которого счет останавливается. И если нечто подобное в математике присутствует, то любопытно узнать, как выглядит, записанное в цифрах, а еще лучше — звучит «по-русски» (или на другом языке). Найти ответ на первую поставленную пытливым умом задачу труда не составит — стоит только вспомнить школьный курс, чтобы понять: если к сколь угодно впечатляющему числу прибавить единицу, то в итоге получено будет число на единицу большее — и так бессчетное количество раз. Напрашивается вывод: поиск самого большого числа в мире — занятие бесконечное, как минимум.
Однако математики нечто подобное искать продолжают и — что любопытно! — находят. Дело в том, что в собственных поисках эти деятели руководствуются не некой абстрактной и недостижимой целью — отыскать самое большое возможное число. Работы ведутся в десятках направлений и с оговорками: ищут то предельного размера число с собственным названием и значением, то максимальное среди простых (натуральных (целых положительных), делящихся только на самих себя и 1), то рекордное из применяемых в математических вычислениях. Другими словами, делают возможное, чтобы не скучать и доказывать целесообразность существования всевозможных математических институтов и профильных факультетов.
О колониальных войнах и русской душе
Заводя разговор о самом большом числе, не обойтись без возвращения к основам, чтобы упростить понимание, ведь большинство людей после окончания института или училища вряд ли пользовались вычислениями сложнее уровня «3 ящика на 7 человек».
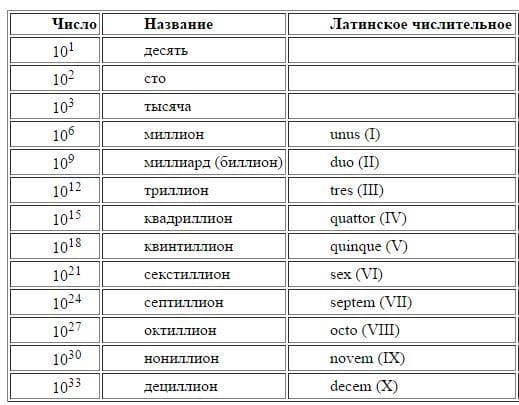
В мире используют два способа наименования чисел — английский и американский. Первый получил большее распространение — в первую очередь потому, что бывшие колонии наследовали привычные принципы. Названия чисел тут образуются путем добавления к латинскому числительному (tres, quattuor, quinque и т. д.) суффикса «-иллион», а к следующему, большему в 1000 раз, — суффикса «-иллиард». Получается чередование: триллион-триллиард, квинтиллион-квинтиллиард. Выбивается из этого правила только первое число: «миллион» происходит от латинского «тысяча» с добавлением соответствующего суффикса — буквально «тысяча тысяч».
В американском способе именования, который распространен в Канаде, Франции и США, суффикс «-иллиард» не используется вовсе, а латинские числительные просто идут по возрастанию. Так получается, что английский «триллиард» равен американскому «квадриллиону», а вместо миллиардеров в США — биллионеры.
В России заимствовать не стеснялись — хотя считается, что в ходу тут американская система, по факту используют смесь: вместо «биллиона» стабильно вставляют в речь «миллиард», да и «триллиарды» периодически «всплывают».
По именам собственным
Разобравшись, как называется то или иное число в «международной системе координат», и поняв, почему переводчики всегда читают надписи в американских фильмах «неправильно», стоит перейти к следующей категории больших чисел — внесистемным.
Оперируя латинскими числительными, можно и дальше продолжать именовать крупные числа, получая сложные составные названия, типа «септемдециллиона» или «октодециллиона». А вот имен собственных получится образовать только три штуки — «вигинтиллион» (10^63 — десять в 63 степени), «центиллион» (10^303) и «миллеиллион» (10^3003). Дальше у древних ромеев в цифрах «затык» — кончаются числительные. Так и выходит, что самое большое число, обладающее несоставным названием, — это 10^3003.
Но дальше к слово(или цифро-)образованию присоединились мыслящие умы, которые придумали давать собственные имена крупным числам, обладающим математическим значением или использующимся в расчетах, типа гравитационной постоянной или «пи». Так появились:
И масса других чисел, используемых в математике для всевозможных расчетов и доказательств, а также система сверхстепеней и другие способы записи столь громоздких значений, именуемые «нотациями».
Так просто, но так сложно
Еще одно направление изучения — поиск самого большого простого числа. Над этим проектом, получившим название Great Internet Mersenne Prime Search (GIMPS), работает Университет центрального Миссури — руководит программой Кертис Купер.
По состоянию на начало 2020-го самым большим простым считается найденное в рамках проекта 7 декабря 2018 года американским программным разработчиком Патриком Ларошем число, которое записывается как 2^82589933-1. Оно — 51-е в ряду чисел Мерсенна, вид которых — 2^n-1, где n — натуральное число. Находка Лароша состоит из 24 862 048 цифр, что на 1,6 миллиона больше, чем у 50-го числа Мерсенна, найденного в 2017 году, которое состоит из 23 249 425.
Проверку новое самое большое простое число прошло за 12 суток. За проделанную работу Патрик Ларош получил 3 тысячи долларов. Впереди у математиков новая цель — отыскать число Мерсенна из 100 миллионов цифр.
Устремленное в бесконечность
Однако перечисленные и неназванные числа покажутся неприметными и невпечатляющими по сравнению с числом Грэма (названо в честь создателя — американского математика Рональда Грэма), записанным в Книгу рекордов Гиннесса в качестве самого большого числа, которое использовалось в математике для доказательства важной гипотезы. Конкретно в этом случае речь идет о теории Фрэнка Рамсея, которая в кратком виде такова: если в N-мерном кубе, где вершины произвольно соединены красными и синими отрезками, закрашивать указанными цветами ребра, то до какого значения N возможно избежать окрашивания плоскости куба одним цветом.
Число Грэма, часто записываемое как G64 или G, приняли в 1977 году. При этом до сих пор математики не способны с достоверной точностью сказать, сколько в этом числе цифр и каких — известны только последние 50: …03222348723967018485186439059104575627262464195387. А вот первые едва ли удастся в обозримом будущем уточнить. Чего стоит только запись этого числа, состоящая из 64 уровней.
Потому не стоит удивляться, что это число иногда сравнивают с бесконечностью — для человеческого мозга разницы при отсчете этих двух величин никакой не будет.