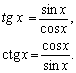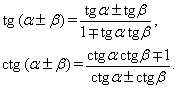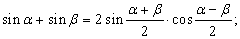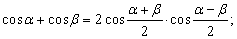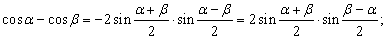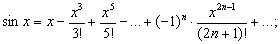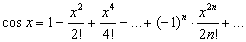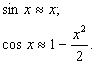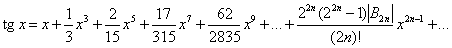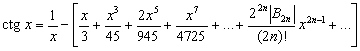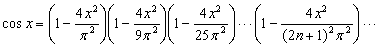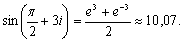Что является тригонометрической функцией формула
Основные тригонометрические формулы и тождества sin, cos, tg, ctg
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
Формулы понижения степени
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Формулы произведения тригонометрических функций
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ – один из классов элементарных функций.
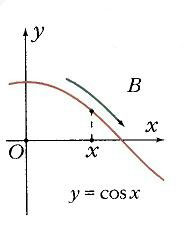
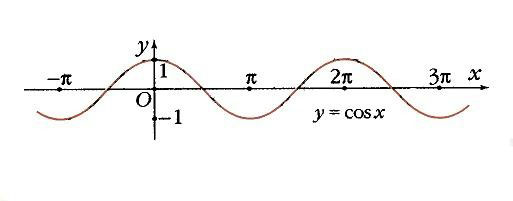
Функция у = cos х.
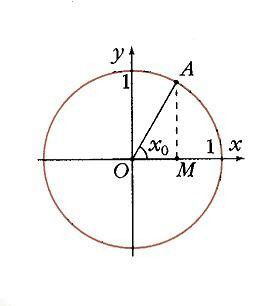
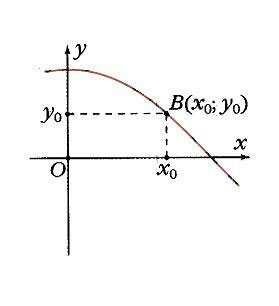
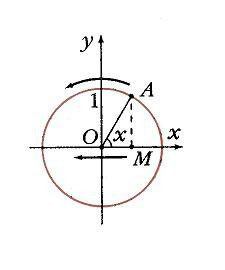
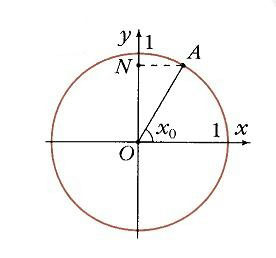
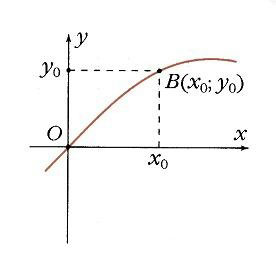
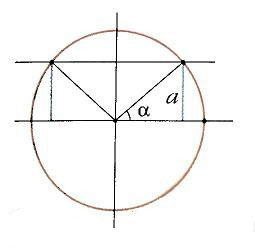
Если построить единичную окружность с центром в начале координат, и задать произвольное значение аргумента x0 и отсчитать от оси Ox угол x0, то этому углу на единичной окружности соответствует некоторая точка A (рис. 1) а ее проекцией на ось Ох будет точка М. Длина отрезка ОМ равна абсолютной величине абсциссы точки A. Данному значению аргумента x0 сопоставлено значение функции y = cos x0 как абсциссы точки А. Соответственно точка В (x0; у0) принадлежит графику функции у = cos х (рис. 2). Если точка А находится правее оси Оу, то косинус будет положителен, если же левее – отрицателен. Но в любом случае точка А не может покинуть окружность. Поэтому косинус лежит в пределах от –1 до 1:
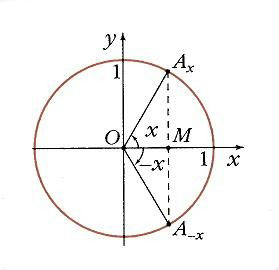
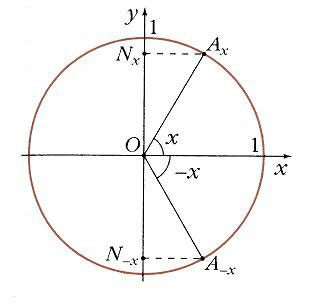
Если взять два значения аргумента, равные по абсолютной величине, но противоположные по знаку, x и –x, найти на окружности соответствующие точки Ax и А-x. Как видно на рис. 3 их проекцией на ось Ох является одна и та же точка М. Поэтому
Значит, можно исследовать свойства функции y = cos х на отрезке [0, p ], а затем учесть ее четность и периодичность.
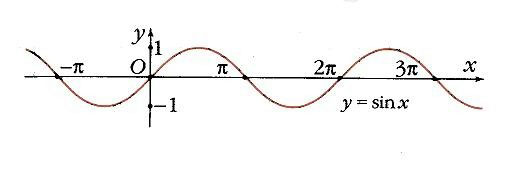
Функция y = sin х.
На единичной окружности углу x0 соответствует точка А (рис. 7), а ее проекцией на ось Оу будет точка N. Значение функции у0 = sin x0 определяется как ордината точки А. Точка В (угол x0, у0) принадлежит графику функции y = sin x (рис. 8). Ясно, что функция y = sin x периодическая, ее период равен 2 p :
т.е. синус – функция нечетная, f(–x) = –f(x) (рис. 9).
Если точку A повернуть относительно точки О на угол p /2 против часовой стрелки (другими словами, если угол х увеличить на p /2), то ее ордината в новом положении будет равна абсциссе в старом. А значит,
Иначе, синус – это косинус, «запоздавший» на p /2, поскольку любое значение косинуса «повторится» в синусе, когда аргумент возрастет на p /2. И чтобы построить график синуса, достаточно сдвинуть график косинуса на p /2 вправо (рис. 10). Чрезвычайно важное свойство синуса выражается равенством
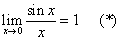
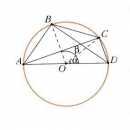
Геометрический смысл равенства виден из рис. 11. Здесь х – это половина дуги АВ, а sin х – половина соответствующей хорды. Очевидно, что по мере сближения точек А и В длина хорды все точнее приближается к длине дуги. Из того же рисунка несложно извлечь неравенство
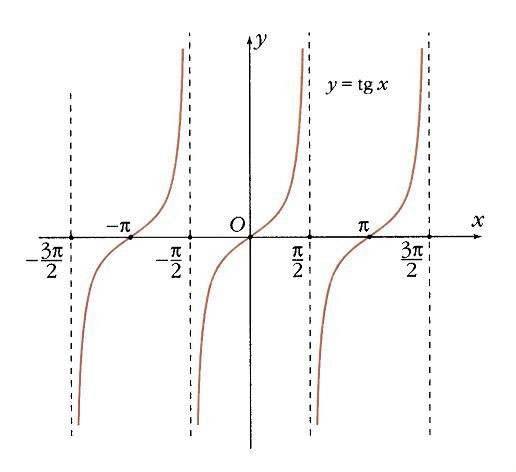
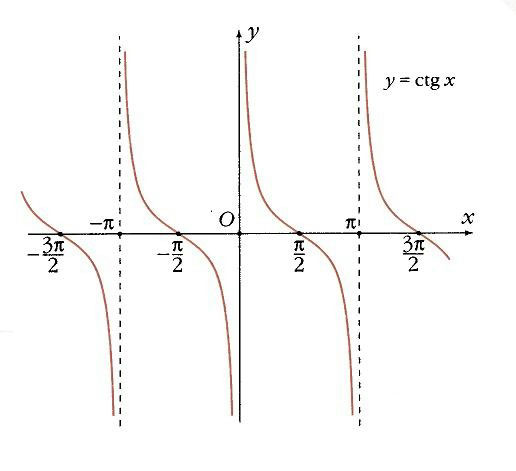
Функции у = tg х, у = ctg х. Две другие тригонометрические функции – тангенс и котангенс проще всего определить как отношения уже известных нам синуса и косинуса:
Котангенс не определен там, где синус равен 0 (когда х = k p ). В остальных точках он монотонно убывает, а прямые х = k p – его вертикальные асимптоты. В точках х = p /2 + k p котангенс обращается в 0, а угловой коэффициент в этих точках равен –1 (рис. 13).
Четность и периодичность.
Функция называется четной, если f(–x) = f(x). Функции косинус и секанс – четные, а синус, тангенс, котангенс и косеканс – функции нечетные:
| sin (–α) = – sin α | tg (–α) = – tg α |
| cos (–α) = cos α | ctg (–α) = – ctg α |
| sec (–α) = sec α | cosec (–α) = – cosec α |
| sin (α + 2kπ) = sin α | cos (α + 2kπ) = cos α |
| tg (α + kπ) = tg α | ctg (α + kπ) = ctg α |
| sec (α + 2kπ) = sec α | cosec (α + 2kπ) = cosec α |
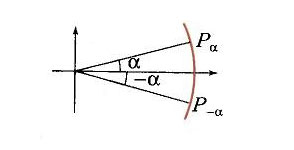
Периодичность синуса и косинуса следует из того, что все точки P a + 2k p , где k = 0, ±1, ±2,…, совпадают, а периодичность тангенса и котангенса – из того, что точки P a + k p поочередно попадают в две диаметрально противоположные точки окружности, дающие одну и ту же точку на оси тангенсов.
Основные свойства тригонометрических функций могут быть сведены в таблицу:
Формулы приведения.
 – a
– a + a
+ a + a
+ a + a
+ a1) название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;
Формулы сложения.
sin ( a 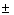
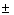
cos ( a 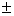
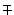
Формулы кратных углов.
Эти формулы выводятся прямо из формул сложения:
sin 2 a = 2 sin a cos a ;
cos 2 a = cos 2 a – sin 2 a = 2 cos 2 a – 1 = 1 – 2 sin 2 a ;
sin 3 a = 3 sin a – 4 sin 3 a ;
cos 3 a = 4 cos 3 a – 3 cos a ;
Если в формулах двойного аргумента заменить a на a /2, их можно преобразовать в формулы половинных углов:
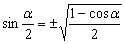
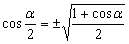
Формулы универсальной подстановки.
Используя эти формулы, выражение, включающее разные тригонометрические функции от одного и того же аргумента, можно переписать как рациональное выражение от одной функции tg ( a /2), это бывает полезно при решении некоторых уравнений:
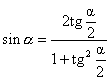 | 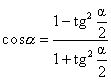 |
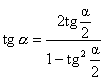 | 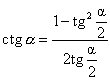 |
Формулы преобразования сумм в произведения и произведений в суммы.
До появления компьютеров эти формулы использовались для упрощения вычислений. Расчеты производились с помощью логарифмических таблиц, а позже – логарифмической линейки, т.к. логарифмы лучше всего приспособлены для умножения чисел, поэтому все исходные выражения приводили к виду, удобному для логарифмирования, т.е. к произведениям, например:
2 sin a sin b = cos ( a – b ) – cos ( a + b );
2 cos a cos b = cos ( a – b ) + cos ( a + b );
2 sin a cos b = sin ( a – b ) + sin ( a + b ).
Формулы для функций тангенса и котангенса можно получить из вышеприведенных.
Формулы понижения степени.
Из формул кратного аргумента выводятся формулы:
| sin 2 a = (1 – cos 2 a )/2; | cos 2 a = (1 + cos 2 a )/2; |
| sin 3 a = (3 sin a – sin 3 a )/4; | cos 3 a = (3 cos a + cos 3 a )/4. |
С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.
| Производные и интегралы тригонометрических функций | |
| (sin x)` = cos x; | (cos x)` = –sin x; |
(tg x)` = 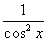 ; ; | (ctg x)` = – 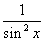 ; ; |
| т sin x dx = –cos x + C; | т cos x dx = sin x + C; |
| т tg x dx = –ln |cos x| + C; | т ctg x dx = ln |sin x| + C; |
Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.
Представление тригонометрических функций в виде степенных рядов и бесконечных произведений.
Все тригонометрические функции допускают разложение в степенные ряды. При этом функции sin x b cos x представляются рядами. сходящимися для всех значений x:
Эти ряды можно использовать для получения приближенных выражений sin x и cos x при малых значениях x:
Функции sin x и cos x могут быть представлены в виде бесконечных произведений:
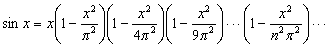
Тригонометрические функции комплексного аргумента
определяются как аналитические продолжения соответствующих тригонометрических функций действительного аргумента в комплексную плоскость. Так, sin z и cos z могут быть определены с помощью рядов для sin x и cos x, если вместо x поставить z:
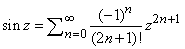
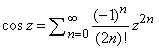
Эти ряды сходятся по всей плоскости, поэтому sin z и cos z – целые функции.
Тангенс и котангенс определяются формулами:
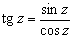
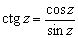
Функции tg z и ctg z – мероморфные функции. Полюсы tg z и sec z – простые (1-го порядка) и находятся в точках z = p /2 + p n, полюсы ctg z и cosec z – также простые и находятся в точках z = p n, n = 0, ±1, ±2,…
Все формулы, справедливые для тригонометрических функций действительного аргумента, справедливы и для комплексного. В частности,
т.е. четность и нечетность сохраняются. Сохраняются и формулы
т.е. периодичность также сохраняется, причем периоды такие же, как и для функций действительного аргумента.
Тригонометрические функции могут быть выражены через показательную функцию от чисто мнимого аргумента:
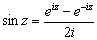
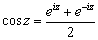
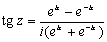
Обратно, e iz выражается через cos z и sin z по формуле:
Эти формулы носят название формул Эйлера. Леонард Эйлер вывел их в 1743.
Тригонометрические функции также можно выразить через гиперболические функции:
z = –i sh iz, cos z = ch iz, z = –i th iz.
где sh, ch и th – гиперболические синус, косинус и тангенс.
Тригонометрические функции комплексного аргумента z = x + iy, где x и y – действительные числа, можно выразить через тригонометрические и гиперболические функции действительных аргументов, например:
Синус и косинус комплексного аргумента могут принимать действительные значения, превосходящие 1 по абсолютной величине. Например:
Если неизвестный угол входит в уравнение как аргумент тригонометрических функций, то уравнение называется тригонометрическим. Такие уравнения настолько часто встречаются, что методы их решения очень подробно и тщательно разработаны. С помощью различных приемов и формул тригонометрические уравнения сводят к уравнениям вида f(x) = a, где f – какая-либо из простейших тригонометрических функций: синус, косинус, тангенс или котангенс. Затем выражают аргумент x этой функции через ее известное значение а.
Поскольку тригонометрические функции периодичны, одному и тому же а из области значений отвечает бесконечно много значений аргумента, и решения уравнения нельзя записать в виде одной функции от а. Поэтому в области определения каждой из основных тригонометрических функций выделяют участок, на котором она принимает все свои значения, причем каждое только один раз, и находят функцию, обратную ей на этом участке. Такие функции обозначают, приписывая приставку агс (дуга) к названию исходной функции, и называют обратными тригонометрическими функциями или просто аркфункциями.
Обратные тригонометрические функции.
Для sin х, cos х, tg х и ctg х можно определить обратные функции. Они обозначаются соответственно arcsin х (читается «арксинус x»), arcos x, arctg x и arcctg x. По определению, arcsin х есть такое число у, что
Аналогично и для других обратных тригонометрических функций. Но такое определение страдает некоторой неточностью.
Если отразить sin х, cos х, tg х и ctg х относительно биссектрисы первого и третьего квадрантов координатной плоскости, то функции из-за их периодичности становятся неоднозначными: одному и тому же синусу (косинусу, тангенсу, котангенсу) соответствует бесконечное количество углов.
Так же решаются другие простейшие тригонометрические уравнения:
где п = 0, ±1, ±2. (рис. 16);
где п = 0, ±1, ±2. (рис. 17);
где п = 0, ±1, ±2. (рис. 18).
Основные свойства обратных тригонометрических функций:
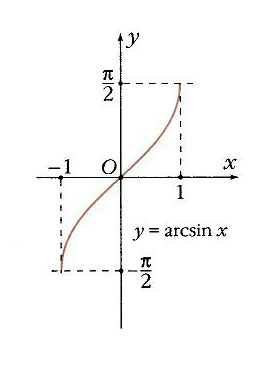
arcsin х (рис. 19): область определения – отрезок [–1, 1]; область значений – [– p /2, p /2], монотонно возрастающая функция;
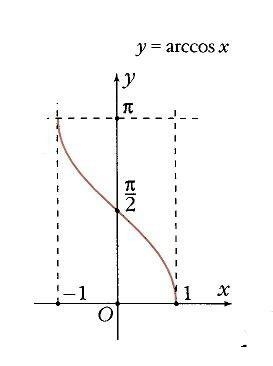
arccos х (рис. 20): область определения – отрезок [–1, 1]; область значений – [0, p ]; монотонно убывающая функция;
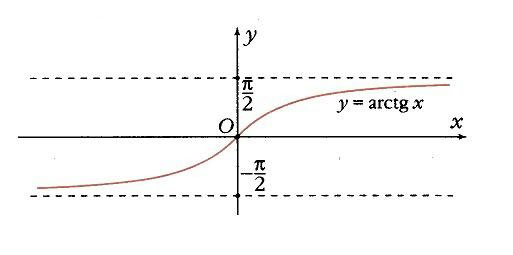
arctg х (рис. 21): область определения – все действительные числа; область значений – интервал (– p /2, p /2); монотонно возрастающая функция; прямые у = – p /2 и у = p /2 – горизонтальные асимптоты;
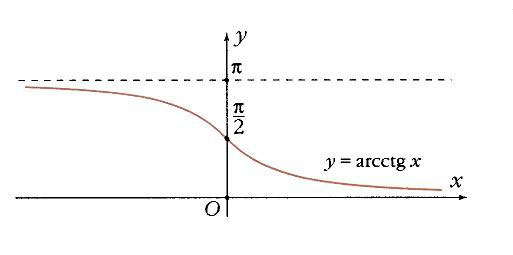
arcctg х (рис. 22): область определения – все действительные числа; область значений – интервал (0, p ); монотонно убывающая функция; прямые y = 0 и у = p – горизонтальные асимптоты.
Т.к. тригонометрические функции комплексного аргумента sin z и cos z (в отличие от функций действительного аргумента) принимают все комплексные значения, то и уравнения sin z = a и cos z = a имеют решения для любого комплексного a:
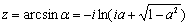
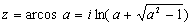
Функции tg z и ctg z принимают все комплексные значения, кроме ±i: уравнения tg z = a, ctg z = a имеют решения для любого комплексного числа a № ± i:
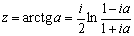
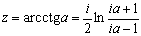
Для любого z = x + iy, где x и y – действительные числа, имеют место неравенства
из которых при y ® Ґ вытекают асимптотические формулы (равномерно относительно x)
Кочетков Е.С., Кочеткова Е. С. Алгебра и элементарные функции, ч. 1–2, М., 1966
Шабат Б.В. Введение в комплексный анализ. М., 1969
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
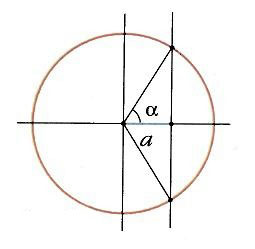
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.