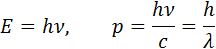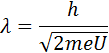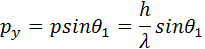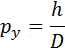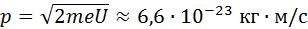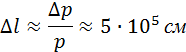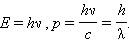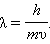де бройль утверждал что волновыми свойствами обладают

Корпускулярно-волновой дуализм свойств материи

Французский ученый Луи де Бройль (1892—1987), осознавая существующую в природе симметрию и развивая представления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.

Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной сторо­ны, корпускулярные характеристики — энергия Е и импульс p, а с другой — волновые характеристики — частота n и длина волны l. Количественные соотношения, связыва­ющие корпускулярные и волновые свойства частиц, такие же, как для фотонов:

Смелость гипотезы де Бройля заключалась именно в том, что соотношение (213.1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:

Это соотношение справедливо для любой частицы с импульсом р.

Вскоре гипотеза де Бройля была подтверждена экспериментально. В 1927 г. американские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кри­сталла никеля, — дает отчетливую дифракционную картину. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов (182.1), а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (213.2). В даль­нейшем формула де Бройля была подтверждена опытами П. С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (энергия »50 кэВ) через металлическую фольгу (толщиной »1 мкм).

Так как дифракционная картина исследовалась для потока электронов, то необходимо было доказать, что волновые свойства присущи не только потоку большой совокупности электронов, но и каждому электрону в отдельности. Это удалось экспериментально подтвердить в 1948 г. российскому физику В. А. Фабриканту (р. 1907). Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других (промежуток времени между двумя электронами в 104 раз больше времени прохождения электроном прибора), возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частице в отдельности.

Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством нали­чия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рас­считываемой по формуле де Бройля (213.2). Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких, как электронография и нейтронография, а также к возникновению новой отрасли науки — электронной оптики.

Экспериментальное доказательство наличия волновых свойств микрочастиц приве­ло к выводу о том, что перед нами универсальное явление, общее свойство материи. Но тогда волновые свойства должны быть присущи и макроскопическим телам. Почему же они не обнаружены экспериментально? Например, частице массой 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с l = 6,62;10–31 м. Такая длина волны лежит за пределами доступной наблюдению области (периодических структур с периодом d»10–31 м не существует). Поэтому считается, что макроскопические тела проявляют только одну сторону своих свойств — корпускулярную — и не проявляют волновую.

Представление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы e и частотой n волн де Бройля:

Это свидетельствует о том, что соотношение между энергией и частотой в формуле (213.3) имеет характер универсального соотношения, справедливого как для фотонов, так и для любых других микрочастиц. Справедливость же соотношения (213.3) вытекает из согласия с опытом тех теоретических результатов, которые получены с его помощью в квантовой механике, атомной и ядерной физике.

Подтвержденная экспериментально гипотеза да Бройля о корпускулярно-волновом дуализме свойств вещества коренным образом изменила представления о свойствах микрообъектов. Всем микрообъектам присущи и корпускулярные, и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в классическом понимании. Современная трактовка корпускулярно-волнового дуализма может быть выражена словами академика В. А. Фока (1898—1974): «Можно сказать, что для атомного объекта существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна—частица. Всякое иное, более буквальное, понимание этого дуализма в вида какой-нибудь модели неправильно».

Источник

Волновые свойства микрочастиц. Дифракция электронов

В 1923 году произошло примечательное событие, которое в значительной степени ускорило развитие квантовой физики. Французский физик Л. де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами.

Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ.

Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:

Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу,

В нерелятивистском приближении (υ –9 г, движущийся со скоростью 0,5 м/с соответствует волна де Бройля с длиной волны порядка 10 –21 м, т. е. приблизительно на 11 порядков меньше размеров атомов. Такая длина волны лежит за пределами доступной наблюдению области. Этот пример показывает, что макроскопические тела могут проявлять только корпускулярные свойства.

Рассмотрим еще один пример. Длина волны де Бройля для электрона, ускоренного разностью потенциалов U = 100 В, может быть найдена по формуле

Это нерелятивистский случай, т. к. кинетическая энергия электрона eU = 100 эВ много меньше энергии покоя mc 2 ≈ 0,5 МэВ. Расчет дает значение λ ≈ 0,1 нм, т. е. длина волны как раз оказывается порядка размеров атомов. Для таких электронов кристаллическое вещество является хорошей дифракционной решеткой. Именно такие малоэнергичные электроны дают отчетливую дифракционную картину в опытах по дифракции электронов. В то же время такой электрон, испытавший дифракционное рассеяние на кристалле как волна, взаимодействует с атомами фотопластинки как частица, вызывая почернение фотоэмульсии в какой-то определенной точке (рис. 5.4.2).

Таким образом, подтвержденная экспериментально гипотеза де Бройля о корпускулярно-волновом дуализме коренным образом изменила представления о свойствах микрообъектов.

Всем микрообъектам присущи и волновые, и корпускулярные свойства, однако, они не являются ни волной, ни частицей в классическом понимании. Разные свойства микрообъектов не проявляются одновременно; они дополняют друг друга, и только их совокупность характеризует микрообъект полностью. В этом заключается сформулированный знаменитым датским физиком Н. Бором принцип дополнительности. Можно условно сказать, что микрообъекты распространяются как волны, а обмениваются энергией как частицы.

С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большее число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может быть дано только на основе понятия вероятности.

Необходимость вероятностного подхода к описанию микрообъектов является важнейшей особенностью квантовой теории. В квантовой механике для характеристики состояний объектов в микромире вводится понятие волновой функции Ψ (пси-функции). Квадрат модуля волновой функции |Ψ| 2 пропорционален вероятности нахождения микрочастицы в единичном объеме пространства. Конкретный вид волновой функции определяется внешними условиями, в которых находится микрочастица. Математический аппарат квантовой механики позволяет находить волновую функцию частицы, находящейся в заданных силовых полях. Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля.

Наиболее отчетливо дифракционные явления проявляются в тех случаях, когда размеры препятствия, на котором происходит дифракция волн, соизмеримы с длиной волны. Это относится к волнам любой физической природы и, в частности, к электронным волнам. Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм). Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты.

Рассмотрим, например, дифракцию электронов на одиночной щели ширины D (рис. 5.4.3).

Рисунок 5.4.3. Дифракция электронов на щели. График справа – распределение электронов на фотопластинке

Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ₁ этого максимума находится из условия

Это формула волновой теории. С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении. Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение py поперечного импульса равно

где p – модуль полного импульса электрона, равный, согласно де Бройлю, h / λ. Величина p при прохождении электрона через щель не меняется, т. к. остается неизменной длина волны λ. Из этих соотношений следует

Квантовая механика вкладывает в это простое на вид соотношение, являющееся следствием волновых свойств микрочастицы, чрезвычайно глубокий смысл. Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δy = D. Величину Δy называют неопределенностью измерения координаты. В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна py или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса и обозначают Δpy. Таким образом, величины Δy и Δpy связаны соотношением

которое называется соотношением неопределенностей Гейзенберга. Величины Δy и Δpy нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса. Соотношение неопределенностей не связано с несовершенством применяемых приборов для одновременного измерения координаты и импульса микрочастицы. Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов. Соотношение неопределенностей позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой в рассмотренном мысленном эксперименте двигался какой-то конкретный электрон после прохождения щели до фотопластинки.

Однако, при определенных условиях соотношение неопределенностей не противоречит классическому описанию движения тел, в том числе и микрочастиц. Например, электронный пучок в кинескопе телевизора при вылете из электронной пушки имеет диаметр D порядка 10 –3 см. В современном телевизоре ускоряющее напряжение U ≈ 15 кВ. Легко подсчитать импульс электрона:

Этот импульс направлен вдоль оси трубки. Из соотношения неопределенностей следует, что электронам при формировании пучка сообщается неконтролируемый импульс Δp, перпендикулярный оси пучка: Δp ≈ h / D ≈ 6,6·10 –29 кг·м/с.

Пусть до экрана кинескопа электроны пролетают расстояние L ≈ 0,5 м. Тогда размытие Δl пятна на экране, обусловленное волновыми свойствами электрона, составит

Поскольку Δl Опубликовано в разделах: Квантовая физика

Источник

Де бройль утверждал что волновыми свойствами обладают

Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:

В нерелятивистском приближении ()

Первое экспериментальное подтверждение гипотезы де Бройля было получено в 1927 году американскими физиками К. Девиссоном и Л. Джермером. Они обнаружили, что пучок электронов, рассеивающийся на кристалле никеля, дает отчетливую дифракционную картину, подобную той, которая возникает при рассеянии на кристалле коротковолнового рентгеновского излучения. В этих экспериментах кристалл играл роль естественной дифракционной решетки. По положению дифракционных максимумов была определена длина волны электронного пучка, которая оказалась в полном соответствии с вычесленной по формуле де Бройля.

В следующем 1928 году английский физик Г. Томсон (сын Дж. Томсона, открывшего за 30 лет до этого электрон) получил новое подтверждение гипотезы де Бройля. В своих экспериментах (рис. 5.4.1) Г. Томсон наблюдал дифракционную картину, возникающую при прохождении пучка электронов через тонкую поликристаллическую фольгу из золота.

На установленной за фольгой фотопластинке отчетливо наблюдались концентрические светлые и темные кольца, радиусы которых изменялись с изменением скорости электронов (т. е. длины волны) согласно де Бройлю (рис. 5.4.2).

В последующие годы опыт Дж. Томсона был многократно повторен с неизменным результатом, в том числе при условиях, когда поток электронов был настолько слабым, что через прибор единовременно могла проходить только одна частица (В. А. Фабрикант, 1948 г.). Таким образом, было экспериментально доказано, что волновые свойства присущи не только большой совокупности электронов, но и каждому электрону в отдельности.

Таким образом, подтвержденная экспериментально гипотеза де Бройля о корпускулярно-волновом дуализме коренным образом изменила представления о свойствах микрообъектов.

С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большее число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может быть дано только на основе понятия вероятности.

Необходимость вероятностного подхода к описанию микрообъектов является важнейшей особенностью квантовой теории. В квантовой механике для характеристики состояний объектов в микромире вводится понятие волновой функции Ψ ( пси-функции ). Квадрат модуля волновой функции пропорционален вероятности нахождения микрочастицы в единичном объеме пространства. Конкретный вид волновой функции определяется внешними условиями, в которых находится микрочастица. Математический аппарат квантовой механики позволяет находить волновую функцию частицы, находящейся в заданных силовых полях. Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля.

Наиболее отчетливо дифракционные явления проявляются в тех случаях, когда размеры препятствия, на котором происходит дифракция волн, соизмеримы с длиной волны. Это относится к волнам любой физической природы и, в частности, к электронным волнам. Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно ). Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты.

Рассмотрим, например, дифракцию электронов на одиночной щели ширины (рис. 5.4.3).

Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина этого максимума находится из условия

Рассмотрим еще один мысленный эксперимент – дифракцию электронного пучка на двух щелях (рис. 5.4.4). Схема этого эксперимента совпадает со схемой оптического интерференционного опыта Юнга.

Анализ этого эксперимента позволяет проиллюстрировать логические трудности, возникающие в квантовой теории. Те же проблемы возникают при объяснении оптического опыта Юнга, исходя из концепции фотонов.

Если в опыте по наблюдению дифракции электронов на двух щелях закрыть одну из щелей, то интерференционные полосы исчезнут, и фотопластинка зарегистрирует распределение электронов, продифрагировавших на одной щели (рис. 5.4.3). В этом случае все электроны, долетающие до фотопластинки, проходят через единственную открытую щель. Если же открыты обе щели, то появляются интерференционные полосы, и тогда возникает вопрос, через какую из щелей пролетает тот или иной электрон?

Психологически очень трудно смириться с тем, что ответ на этот вопрос может быть только один: электрон пролетает через обе щели. Мы интуитивно представляем себе поток микрочастиц как направленное движение маленьких шариков и применяем для описания этого движения законы классической физики. Но электрон (и любая другая микрочастица) обладает не только корпускулярными, но и волновыми свойствами. Легко представить, как электромагнитная световая волна проходит через две щели в оптическом опыте Юнга, т. к. волна не локализована в пространстве. Но если принять концепцию фотонов, то мы должны признать, что каждый фотон тоже не локализован. Невозможно указать, через какую из щелей пролетел фотон, как невозможно проследить за траекторией движения фотона до фотопластинки и указать точку, в которую он попадет. Опыт показывает, что даже в том случае, когда фотоны пролетают через интерферометр поштучно, интерференционная картина после пролета многих независимых фотонов все равно возникает. Поэтому в квантовой физике делается вывод: фотон интерферирует сам с собой.

Источник

Корпускулярно-волновой дуализм

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: гипотеза де Бройля о волновых свойствах частиц, корпускулярно-волновой дуализм, дифракция электронов.

Корпускулярно-волновой дуализм (слово дуализм означает двойственность) — это физический принцип, утверждающий, что любой объект природы может вести себя и как частица, и как волна.

С первым проявлением этого принципа мы столкнулись в предыдущем листке, когда говорили о двойственной, корпускулярно-волновой природе света. В явлениях интерференции и дифракции свет демонстрирует свою волновую природу. В явлении фотоэффекта свет выступает как дискретный поток частиц — фотонов.

Является ли свет каким-то особым объектом нашего мира, таким, что подобный дуализм присущ только ему? Или, быть может, корпускулярно-волновой дуализм — это свойство вообще всех материальных объектов, просто впервые обнаружен он был для света?

Гипотеза де Бройля

Идея об универсальной двойственности корпускулярных и волновых свойств всех объектов природы была впервые высказана Луи де Бройлем (в 1924году) в качестве гипотезы о волновых свойствах частиц.

Гипотеза де Бройля. Движению каждой частицы соответствует распространение некоторой волны. Частота и длина этой волны определяются энергией и импульсом частицы:

Чтобы лучше осмыслить гипотезу де Бройля, давайте обсудим дуализм «волна–частица» на примере электромагнитного излучения.

В случае электромагнитных волн мы имеем следующую закономерность. По мере увеличения длины волны всё легче наблюдать волновые свойства излучения и всё труднее — корпускулярные. И наоборот, чем меньше длина волны, тем ярче выражены корпускулярные свойства излучения и тем труднее наблюдать его волновые свойства. Изменение соотношения корпускулярных и волновых свойств хорошо прослеживается при движении по известной вам шкале электромагнитных волн.

• Радиоволны.Длины волн здесь настолько велики, что корпускулярные свойства излучения практически не проявляются. Волновые свойства в этом диапазоне абсолютно доминируют.

Длины волн могут составлять несколько метров или даже километров, так что волновая природа проявляется «сама собой» — радиоволны в процессе дифракции запросто огибают дома или горы. Излучение радиоволн и их взаимодействие с материальными объектами отлично описывается в рамках классической электродинамики.

• Видимый свет и ультрафиолет. Это своего рода «переходная область»: в оптике мы можем наблюдать как волновые свойства света, так и корпускулярные.

Однако в обоих случаях надо постараться. Так, длины волн видимого света много меньше размеров окружающих нас тел, поэтому в опытах по интерференции или дифракции света нужно создавать специальные условия (малость щелей или отверстий, удалённость экрана). В свою очередь, термин «красная граница фотоэффекта» также подчёркивает пограничность данного диапазона: фотоэффект начинается лишь при переходе через красную границу.

• Рентгеновское и гамма-излучение. Длины волн очень малы, и наблюдать волновые свойства излучения весьма затруднительно. Так, верхняя граница длин волн рентгеновского излучения составляет нм; это лишь на два порядка превышает размер атома. Ясно, что дифракцию на «обычных» препятствиях при такой длине волны наблюдать невозможно.

Однако в рентгеновский диапазон входят длины волн порядка размера атома и межатомных расстояний в кристалле ( нм). Поэтому дифракция рентгеновских лучей наблюдается на «естественных» дифракционных решётках — кристаллических решётках твёрдых тел (эта идея была высказана немецким физиком Лауэ в 1912 году).

Энергия квантов в рентгеновском и гамма-диапазоне настолько велика, что излучение ведёт себя почти стопроцентно как поток частиц.

Рассуждая по аналогии с электромагнитными волнами, можно заключить, что и частица будет проявлять волновые свойства тем лучше, чем больше её длина волны де Бройля (в масштабах данной ситуации).

Так, мы совсем не наблюдаем волновых свойств у окружающих нас тел. (Видели вы, например, интерференцию движущихся автомобилей?) А почему? Давайте посчитаем длину дебройлевской волны объекта массой кг, движущегося со скоростью м/с:

Это на порядков меньше размера атома. Воображение отказывается представить себе столь малую величину. Разумеется, никакого волнового поведения у нашего объекта при таких условиях не обнаруживается — он стопроцентно ведёт себя как «частица», то есть как материальная точка классической механики.

Дифракция электронов

Совсем другое дело — электрон. Масса электрона равна кг, и столь малое значение массы (а стало быть, и импульса в формуле ) может дать длину волны де Бройля, достаточную для экспериментального обнаружения волновых свойств.

И вот оказывается, что электроны с энергией эВ (при такой энергии становится несущественным хаотическое тепловое движение электронов, и электронный пучок можно считать когерентным) имеют дебройлевскую длину волны примерно нм — это как раз порядка размера атома и расстояний между атомами в кристаллической решётке! Опыт по наблюдению дифракции рентгеновских лучей на кристаллических структурах уже имелся, поэтому оставалось направить на кристаллическую решётку пучок электронов.

Впервые это было сделано в знаменитом эксперименте американских физиков Дэвиссона и Джермера (1927 год). Дифракция электронов на кристаллах была обнаружена! Как и ожидалось, полученная дифракционная картина имела тот же характер, что и при дифракции на кристаллической решётке рентгеновских лучей.

Впоследствии волновые свойства были обнаружены и у более крупных частиц: протонов, нейтронов, атомов и молекул. Гипотеза де Бройля, таким образом, получила надёжное опытное подтверждение.

Соотношение неопределённостей

Обнаружение корпускулярных свойств электромагнитных волн и волновых свойств частиц показало, что объекты микромира подчиняются необычным законам. Эти законы совершенно непривычны для нас, привыкших наблюдать за макроскопическими телами.

Наше сознание выработало некоторые образы частицы и волны, вполне пригодные для описания объектов классической физики. Частица — это маленький, локализованный в пространстве сгусток вещества. Волна — это распределённый (не локализованный) в пространстве колебательный процесс. Как же эти понятия могут совмещаться в одном объекте (например, в электроне)?

Вообразить такое действительно получается с трудом. Но что поделать — это факт. Природа оказывается намного богаче нашего воображения. В своей повседневной жизни мы находимся очень далеко от микромира, и в привычном нам диапазоне макроскопических тел природа демонстрирует свои «крайние» проявления — в виде «только частиц» или «только волн». Вот почему корпускулярные и волновые свойства представляются нам несовместимыми друг с другом. Но на самом деле это не так: в микромире оказывается, что один и тот же объект (например, электрон) легко может обладать обоими свойствами одновременно — словно человек, обладающий разными, несовместимыми на первый взгляд чертами характера.

Так, будучи частицей, электрон локализован в пространстве; но, будучи волной, локализован не в точке, а «размазан» по некоторой области. Координаты и скорость электрона не могут быть измерены одновременно сколь угодно точно. Неопределённость координаты и неопределённость соответствующей проекции импульса оказываются связанными соотношением неопределённостей Гейзенберга:

Соотношение неопределённостей (2) имеет фундаментальный характер — оно применимо к любым объектам природы. Чем точнее мы знаем координаты объекта (то есть чем в меньшей пространственной области он локализован), тем больше получается разброс значений его импульса(то есть тем с большей скоростью объект «готов вылететь» из этой области). И наоборот, чем точнее мы знаем импульс объекта, тем меньше у нас информации о том, где этот объект находится.

Но коль скоро нет возможности одновременно точно измерить координаты и скорость, то теряет смысл понятие траектории движения объекта. Механика Ньютона перестаёт работать в микромире и уступает место квантовой механике.

Источник