декартово произведение это что
Декартово произведение множеств
Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.
Содержание
Прямое произведение в теории множеств
Произведение двух множеств
| в | в | в | в | в | в | в | в |
|---|---|---|---|---|---|---|---|
| и | и | и | и | и | и | и | и |
| к | к | к | к | к | к | к | к |
| Произведение множества <в, и, к> на множество цветов радуги | |||||||
Отображения произведения множеств в его множители ( 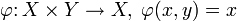
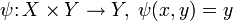
Аналогично строятся произведения нескольких множеств.
Декартова степень
Прямое произведение семейства множеств
Прямое произведение отображений
Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.
Воздействие на математические структуры
Прямое произведение групп
Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.
Прямое произведение других алгебраических структур
Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.
Прямое произведение топологических пространств
Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).
Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).
Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).
Прямое произведение графов
Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:
Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.
Вариации и обобщения
Декартово произведение
Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.
Содержание
Прямое произведение в теории множеств
Произведение двух множеств
| в | в | в | в | в | в | в | в |
|---|---|---|---|---|---|---|---|
| и | и | и | и | и | и | и | и |
| к | к | к | к | к | к | к | к |
| Произведение множества <в, и, к> на множество цветов радуги | |||||||
Отображения произведения множеств в его множители ( 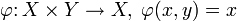
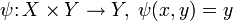
Аналогично строятся произведения нескольких множеств.
Декартова степень
Прямое произведение семейства множеств
Прямое произведение отображений
Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.
Воздействие на математические структуры
Прямое произведение групп
Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.
Прямое произведение других алгебраических структур
Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.
Прямое произведение топологических пространств
Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).
Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).
Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).
Прямое произведение графов
Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:
Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.
Вариации и обобщения
Декартово (прямое) произведение множеств



ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ. СООТВЕТСТВИЯ, ФУНКЦИИ, ОТНОШЕНИЯ
ЦЕЛЬ ЛЕКЦИИ – изучение свойств декартова произведения множеств, и связанных с ним соответствий, функций и отношений.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Помимо рассмотренных в первой лекции традиционных операций над множествами существуют и другие действия с множествами, которые позволяют решать много задач, имеющих практическое применение. В частности, к таким действиям относится декартово (прямое) произведение множеств. Свое название декартово произведение получило оттого, что предложенное Декартом координатное представление точек плоскости, являлось исторически первым примером прямого произведения.
Декартово (прямое) произведение множеств
Декартово (прямое) произведение множеств Х и 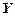
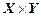
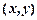
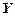
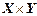
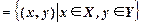
Согласно определению элементами прямого произведения множеств являются упорядоченные пары, составленные из элементов исходных множеств. В этих парах первый элемент (компонента) всегда принадлежит первому множеству, а второй элемент (компонента) второму. Порядок множеств определяется исходной записью и, если 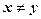
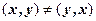
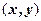
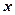
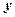
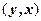
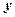
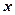
Множество 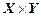
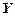
Геометрическое представление этого множества приведено на рис. 2.1, а.
Пример 2.2. Пусть A и B – отрезки вещественной оси. Прямое произведение изобразится заштрихованным прямоугольником, показанным на рис. 2.1, б.
Пример 2.3. Найти декартово произведение множеств 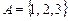
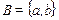
Решение. A × B 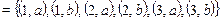
Порядок перечисления элементов безразличен, важен только порядок элементов в паре (упорядоченная пара).
B × A 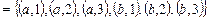
Из приведенных примеров видно, что свойства прямого произведения отличаются от свойств обычного произведения в арифметическом смысле. В частности, прямое произведение изменяется при изменении порядка сомножителей, то есть 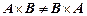
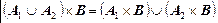
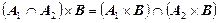
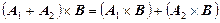
Прямое произведение множеств – операция многоместная
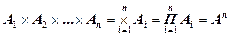
В результате получаются множества, состоящие из упорядоченной последовательности вида
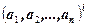
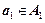
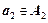
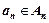
Такие последовательности называются кортежами или векторами.
Кортеж длины 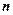
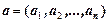
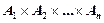
Сами элементы при этом называются компонентами (координатами) кортежа, которые нумеруются слева направо (первая компонента, вторая компонента и т.д.).
Примеры кортежей: множество людей, стоящих в очереди, числа, выражающие координаты точки на плоскости и т.п. Во всех этих множествах место каждого элемента является вполне определенным и не может быть произвольно изменено.
Основные отличия понятий кортежа (вектора) и множества заключаются в следующем:
1) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны, даже в случае, когда они имеют одинаковый состав;
2) в множестве все элементы различны, а в кортеже координаты могут повторяться.
Таким образом, в отличии от обычного множества в кортеже (векторе) могут быть одинаковые компоненты: два одинаковых слова в фразе, одинаковые численные значения координат точки на плоскости и т.п.
Таким образом, декартово произведение позволяет получать вектора любых размерностей. Эта операция отличается от операций объединения и пересечения тем, что в результате перемножения прямым способом получаются объекты, содержащие элементы, отличающиеся по своей природе от элементов исходных множеств.
Если перемножить n раз одно и то же множество, то получится множество 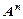
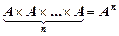
Степенью декартового произведения называется число множеств n, входящих в это декартово произведение.
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ
Смотреть что такое «ДЕКАРТОВО ПРОИЗВЕДЕНИЕ» в других словарях:
декартово произведение — Декартовым (или прямым) произведением называется выборка всех возможных комбинаций строк из двух таблиц. Оно получается, если единственное существующее отношение между двумя таблицами деактивизируется, а затем выполняется запрос, использующий… … Справочник технического переводчика
Декартово произведение — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Декартово произведение множеств — [cartesian product] произведение множеств A ´ B, рассматриваемое как множество всех упорядоченных пар элементов (a, b), из которых a принадлежит множеству A, b множеству B. Порядок следования пар может быть любым, но расположение элементов в… … Экономико-математический словарь
декартово произведение двух множеств — Прямое или декартово произведение множеств, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие широко благодаря тому, что прямое произведение часто наследует структуры (алгебраические,… … Справочник технического переводчика
Декартово произведение групп — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Декартово произведение множеств — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Произведение (теория категорий) — Произведение двух или более объектов это обобщение в теории категорий таких понятий, как декартово произведение множеств, прямое произведение групп и произведение топологических пространств. Произведение семейства объектов это в… … Википедия
Произведение мер — в функциональном анализе, теории вероятностей и смежных дисциплинах формальный способ построить меру на декартовом произведении двух пространств с мерами. Содержание 1 Построение 2 Замечания 3 Пример … Википедия
Лекция 2. Декартово произведение. Мощность множества
п.2. Декартово произведение. Мощность множества.
2.1. Декартово произведение множеств.
Упорядоченная пара 


Определение 2.1. Пусть A и B – два множества. Прямым (декартовым) произведением двух множеств A и B называется множество всех упорядоченных пар, в котором первый элемент каждой пары принадлежит A, а второй принадлежит B:
Пример. Пусть 



Пример. На координатной плоскости построить следующее множество:
Решение. Первое множество помещаем на оси OX, второе на оси OY. Множество всех пар, т. е. декартово произведение, изображается точками заштрихованного прямоугольника, но без левой и нижней стороны.








 . Метод координат ввел в употребление Рене Декарт (), отсюда и название «декартово произведение».
. Метод координат ввел в употребление Рене Декарт (), отсюда и название «декартово произведение». .
. .
. и вообще
и вообще  .
. (
(  – первая буква древнееврейского алфавита, называемая «алеф», символ
– первая буква древнееврейского алфавита, называемая «алеф», символ  читается: «алеф-нуль»). В частности |N|=
читается: «алеф-нуль»). В частности |N|= .
. . Следующую теорему примем без доказательства.
. Следующую теорему примем без доказательства. – конечные попарно непересекающиеся множества, т. е.
– конечные попарно непересекающиеся множества, т. е.  . Тогда
. Тогда (2.3.1.)
(2.3.1.) . Тогда
. Тогда (2.3.2.)
(2.3.2.) и множества S1, S2 и S3 попарно непересекающиеся, то
и множества S1, S2 и S3 попарно непересекающиеся, то .
. , которые могут иметь непустые пересечения между собой, т. е. объединение может быть не разбиением. В общем случае имеет место следующая теорема, которую нетрудно доказать методом математической индукции.
, которые могут иметь непустые пересечения между собой, т. е. объединение может быть не разбиением. В общем случае имеет место следующая теорема, которую нетрудно доказать методом математической индукции.  , справедлива формула включений и исключений.
, справедлива формула включений и исключений. (2.3.3.)
(2.3.3.) .
. .
. .
. .
. .
. . Множество X1ÇX3 – множество положительных целых чисел, которые делятся на 2 или 5. Число элементов или мощность этого множества равно
. Множество X1ÇX3 – множество положительных целых чисел, которые делятся на 2 или 5. Число элементов или мощность этого множества равно  . Множество X2ÇX3 – множество положительных целых чисел, которые делятся на 3 или 5. Число элементов или мощность этого множества равно
. Множество X2ÇX3 – множество положительных целых чисел, которые делятся на 3 или 5. Число элементов или мощность этого множества равно  .
. .
. . Элементы универсума нумеруются:
. Элементы универсума нумеруются: – это i-й разряд кода C.
– это i-й разряд кода C.