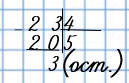деление в столбик что делать с остатком

Деление натуральных чисел с остатком: правило, примеры решений

Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.

Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.

Деление натуральных чисел столбиком с остатком

Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.

Приведем решение примера, так как понять суть метода проще всего на практике.

Пример 1. Как делить натуральные числа с остатком?

Проводим деление столбиком и записываем:

Деление чисел с остатком через последовательное вычитание

Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.

Пример 2. Деление с остатком через последовательное вычитание.

Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.

Пример 3. Деление с остатком через последовательное вычитание.

Повторяем эту операцию еще раз:

Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.

12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)

Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.

Метод подбора неполного частного

При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.

В-третьих, не будем забывать, что остаток всегда меньше делителя.

Разберем применение этого метода на примере.

Пример 4. Деление с остатком методом подбора

Алгоритм деления натуральных чисел с остатком

Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.

Сформулируем три вопроса и ответим на них:

Запомним это число.

2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.

Число, которое мы получили на предпоследнем шаге ( 470 = 47 · 10 ) является первым из искомых слагаемых.

5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.

3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы

899 = 47 · 10 + 47 · 9 + 6

Применим распределительное свойство умножения.

899 = 47 · 10 + 47 · 9 + 6 = 47 · ( 10 + 9 ) + 6

Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:

Пример 5. Деление натуральных чисел с остатком

В результате получаем:

42252 = 40800 + 1360 + 68 + 24 = 68 · 600 + 68 · 20 + 68 · 1 + 24 = = 68 · ( 600 + 20 + 1 ) + 24 = 68 · 621 + 24

Деление натуральных чисел с остатком. Проверка результата

Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.

На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.

Остаток всегда меньше делителя!

Пример 6. Проверка результата деления натуральных чисел с остатком.

Значит, деление выполнено неверно.

Первый пункт проверки пройден, переходим ко второму.

Подставляем значения и сравниваем результаты

13 · 9 + 5 = 117 + 5 = 122 ; 121 ≠ 122

Значит, в вычисления школьника где-то закралась ошибка.

После подстановки, имеем:

Равенство корректно, а значит, и деление выполнено верно.

Источник

Деление с остатком

Начнём рассмотрение новой темы с решения задачи.

Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?

Каждый ребёнок получил по 4 конфеты.

На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?

Каждый получил по 2 конфеты и 2 конфеты остались лишними.

Как сделать проверку?

Правило 1

Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.

Правило 2

При делении с остатком остаток всегда должен быть меньше делителя.

Порядок решения

1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.

2. Вычитаю из делимого найденное число: 14 − 10 = 4

3. Сравниваю остаток с делителем

Проверка деления с остатком

1. Умножаю неполное частное на делитель.

2. Прибавляю остаток к полученному результату.

3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.

Деление в столбик

В 23 содержится 5 раз по 4, и ещё остаётся 3.

Решение записывают так:

23 : 4 = 5 (ост. 3) или так:

Поделись с друзьями в социальных сетях:

Источник

Деление в столбик

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.

Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза.

Проверяем: 4 × 7 = 28, а 28

Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся двойку и продолжаем размышлять.

Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Как выглядит деление в столбик с остатком

Это такое же деление, только в результате получается неровное число, как получилось в примере выше.

Примеры на деление в столбик

Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!

Источник

Деление чисел с остатком

Деление с остатком целых положительных чисел

Деление — это разбиение целого на равные части.

Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.

Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!

Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.

Попрактикуемся в решении.

Пример

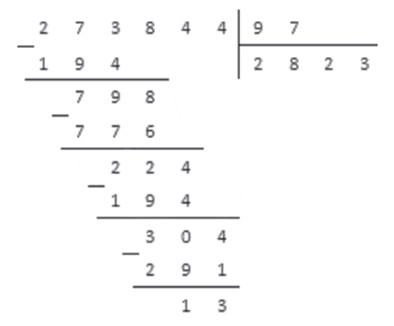
Разделить 14671 на 54.

Выполним деление столбиком:

Неполное частное равно 271, остаток — 37.

Ответ: 14671 : 54 = 271(остаток 37).

Деление с остатком положительного числа на целое отрицательное

Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:

В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.

Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.

Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».

Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.

Алгоритм деления положительного числа на целое отрицательное (с остатком):

Пример

Разделить 17 на −5 с остатком.

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.

Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.

Ответ: 17 : (− 5) = −3 (остаток 2).

Деление с остатком целого отрицательного числа на целое положительное

Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:

Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:

d = a − b * c

Из правила делаем вывод, что при делении получается целое неотрицательное число.

Для точности решения применим алгоритм деления а на b с остатком:

Рассмотрим пример, где можно применить алгоритм.

Пример

Найти неполное частное и остаток от деления −17 на 5.

Разделим заданные числа по модулю.

Получаем, что при делении частное равно 3, а остаток 2.

Так как получили 3, противоположное ему −3.

Необходимо отнять единицу: −3 − 1 = −4.

Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:

d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.

Значит, неполным частным от деления является число −4 с остатком 3.

Ответ: (−17) : 5 = −4 (остаток 3).

Деление с остатком целых отрицательных чисел

Сформулируем правило деления с остатком целых отрицательных чисел:

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:

d = a − b * c

Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.

Алгоритм деления с остатком целых отрицательных чисел:

Пример

Найти неполное частное и остаток при делении −17 на −5.

Применим алгоритм для деления с остатком.

Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.

Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.

Получилось, что остаток равен 3, а неполное частное равно 4.

Ответ: (−17) : (−5) = 4 (остаток 3).

Деление с остатком с помощью числового луча

Деление с остатком можно выполнить и на числовом луче.

Пример 1

Рассмотрим выражение: 10 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.

Решение: 10 : 3 = 3 (остаток 1).

Пример 2

Рассмотрим выражение: 11 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.

Решение: 11 : 3 = 3 (остаток 2).

Проверка деления с остатком

Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.

Формула деления с остатком

a = b * c + d,

где a — делимое, b — делитель, c — неполное частное, d — остаток.

Эту формулу можно использовать для проверки деления с остатком.

Пример

Рассмотрим выражение: 15 : 2 = 7 (остаток 1).

В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:

Теорема о делимости целых чисел с остатком

Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.

Теорема

Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:

где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.

Доказательство:

Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.

Тогда необходимо взять q такое, чтобы данное неравенством b * q

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

План урока:

Здравствуйте, ребята. Я, Знайка, продолжаю учить вас математике.

Выражение «твердый орешек» означает трудную для решения задачу. Орешек знанья тверд, но мы не привыкли отступать, вместе его расколем. Пусть скорлупа ореха — символ знания, ядро — опыт человечества. Математика раскроет тайны деления двузначных чисел, если будем стараться. Французский ученый Декарт говорил: «Умейте использовать свой хороший ум, чтобы справиться с задачами».

Случаи деления 80 : 20, 87 : 29

Начнем с деления на двузначное число.

Приемы деления вида 80 : 20

Приемы деления вида 87 : 29

Найдите значения двух выражений:

Для решения посмотрите на цифры единиц. Делитель заканчивается на 9. Вспомните таблицу умножения девяти. Какое произведение имеет семерку на конце? 27.

Других вариантов в таблице умножения на девять нет. Ответ равен трем.

Внимательно посмотрите на цифры в единицах. Делимое заканчивается на четверку. Вспомните множитель, который при умножении шести в произведении дает последнюю цифру четверку.

Это два случая: четыре, девять. В значениях произведений четверка на конце. Какой множитель подходит? Давайте посмотрим. Девять — многовато.

Задания легко решать, если знаешь таблицу умножения.

Деление столбиком на двузначное число

Вы уже знаете, что для записи действия деления применяют математический символ в виде двоеточия (∶), обелюса (÷), дробной (–), косой (∕) черты. Сегодня мы используем знак, который похож на лежащую боком букву.

При делении столбиком очень важна аккуратность, поэтому возьмите листок в клеточку.

Как записать решение примера 32 : 16 столбиком? Запишите каждую цифру делимого 32 в отдельную клеточку. Отступите одну клеточку вправо, запишите делитель 16. Проведите вертикальную и горизонтальную черточку.

Подбираем частное. Посмотрите на цифры единиц 2 и 6. Вспомните табличные случаи.

Семерка нам не подойдет, потому что 16 ∙ 7 — это большая величина. Значит, выбираем двойку. Проверяем: 16 ∙ 2 = 32. Записываем двойку на место частного под чертой. Вычитаем 32 из делимого. Пишем нуль. 32 разделили нацело.

Хорошо. А знаете ли вы, что с древних времён замечено влияние грецкого ореха на работу мозга. Как будто природа создала его, по форме извилин напоминающим полушария головного мозга. Благодаря работе этого центрального органа мы справляемся с математическими задачами.

Деление с остатком

Ребята, я предлагаю вам отправиться в путешествие по реке на лодках. Прежде чем отплыть от берега, нам нужно разделить 9 спасательных кругов на 2 лодки. Как узнать, сколько кругов окажется в одной лодке?

Верно, надо разделить. Запишите решение. Сколько получилось в выражении?

У вас трудности. Что заметили?

9 на 2 нацело не делится.

Почему не можем найти значение данного выражения?

Потому что это не табличный случай. Мы не умеем решать такие выражения.

Ребята, оказывается, в примерах может получиться остаток. Это арифметическое действие, играющее большую роль в математике и криптографии — науке о защите информации. В компьютерной технике тоже часто решают данные выражения.

Напишите отрезок натурального ряда от 17 до 37.

Выпишите из этого отрезка числа, которые делятся на 9.

Проверьте, это — 18, 27, 36.

Остаток при делении натуральных чисел 19, 28, 37 на 9 равен единице, потому что они следующие при счете.

Запишите отрезок натурального ряда от 11 до 25. Обведите числа, которые делятся на шесть нацело.

Укажите остатки при делении на 6 тринадцати и четырнадцати. Запишите выражения.

Проверьте:

Объясните, как рассуждали.

15 — на третьем месте после 12, 16 — четвертое место, а 17 – пятое место после 12.

Какой самый большой остаток получается при делении на 6?

Это пять, так как между величинами, которые делятся на шесть нацело, находится пять чисел.

Интересно знать! В Древнем Египте кушать ядра грецких орехов могли только высшие, самые главные жрецы. Для всех остальных, особенно для простого народа — это было запрещено. Чтобы не становились умнее и не начали много думать. Но мы с вами знаем пользу орехов и хорошо соображаем, поэтому продолжаем урок.

Деление с остатком на однозначное число

Существует два способа решения примеров.

1 способ деления на 5, 6, 7, 8, 9

Первый способ подходит, когда делитель равен или больше пяти. Мы должны найти в делимом наибольшее число, чтобы разделить, например, на семерку.

Как его отыскать? Посчитайте семерками. Если бы делили на пять, то считали бы пятерками, на шесть – шестерками и так далее.

Разве 41 разделить на 7 — это пять? Нет, мы разделили только 35. Теперь найдем, сколько не разделили. Из 41 отнимите 35, получится шесть. Это искомый остаток.

Сделайте обязательный шаг — убедитесь, что остаток получился меньше чем делитель. Действительно 6 1 2

Источник