децимация что это в математике
Курс лекций «Основы цифровой обработки сигналов»
Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.
Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.
Список лекций
Этот курс содержит материалы в виде законченных лекций по разным тематикам из области цифровой обработки сигналов. Материалы представлены с использованием библиотек на языке Python (пакеты numpy, scipy, matplotlib, и т.д.). Основная информация для этого курса взята из моих лекций, которые я, будучи аспирантом, читал студентам Московского Энергетического Института (НИУ МЭИ). Частично информация из этих лекций была использована на обучающих семинарах в Центре Современной Электроники, где я выступал в качестве лектора. Кроме того, в этот материал входит перевод различных научных статей, компиляция информации из достоверных источников и литературы по тематике цифровой обработки сигналов, а также официальная документация по прикладным пакетам и встроенным функциям библиотек scipy и numpy языка Python.
Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из Python-библиотек.
Все материалы сгруппированы по основным тематикам цифровой обработки сигналов:
Список лекций — достаточный но, разумеется, неполный для вводного знакомства с областью ЦОС. При наличии свободного времени я планирую поддерживать и развивать этот проект.
Где найти?
Все материалы — абсолютно бесплатны и доступны в виде открытого репозитория на моем гитхабе как opensource проект. Материалы представлены в двух форматах — в виде тетрадок Jupyter Notebook для интерактивной работы, изучения и редактирования, и в виде скомпилированных из этих тетрадок HTML-файлов (после скачивания с гитхаба имеют вполне пригодный формат для чтения и для печати).
Ниже приводится очень краткое описание разделов курса с небольшими пояснениями, терминами и определениями. Основная информация доступна в исходных лекциях, здесь представлен лишь краткий обзор!
Сигналы. Z-преобразование
Вводный раздел, в котором содержится основная информация по типам сигналов. Вводится понятие дискретной последовательности, дельта-функции и функции Хевисайда (единичный скачок).
Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема отсчетов, известная как Теорема Котельникова (Найквиста-Шеннона).
Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.
Такая трактовка справедлива при условии, что непрерывная функция времени занимает полосу частот от 0 до значения верхней частоты. Если шаг квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную будет происходить с искажениями.
Также в этом разделе описывается Z-преобразование и его свойства, показывается представление дискретных последовательностей в Z-форме.
Пример конечной дискретной последовательности:
.
Пример этой же последовательности в Z-форме:
Преобразование Фурье. Свойства. ДПФ и БПФ
В этом разделе описывается понятие временной и частотной области сигнала. Вводится определение дискретного преобразования Фурье (ДПФ). Рассмотрены прямое и обратное ДПФ, их основные свойства. Показан переход от ДПФ к алгоритму быстрого преобразования Фурье (БПФ) по основанию 2 (алгоритмы децимации по частоте и по времени). Отражена эффективность БПФ в сравнении с ДПФ.
В частности, в этом разделе описывается Python пакет scipy.ffpack для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное, многомерное, вещественное).
Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.
Особенности спектров дискретных сигналов:
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность вещественная, то модуль спектральной плотности такой последовательности есть четная функция, а аргумент – нечетная функция частоты.
Спектр гармонического сигнала:
Сравнение эффективности ДПФ и БПФ
Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N:
| N | ДПФ | БПФ | Отношение числа комплексных сложений | Отношение числа комплексных умножений | ||
|---|---|---|---|---|---|---|
| Число операций умножения | Число операций сложения | Число операций умножения | Число операций сложения | |||
| 2 | 4 | 2 | 1 | 2 | 4 | 1 |
| 4 | 16 | 12 | 4 | 8 | 4 | 1.5 |
| 8 | 64 | 56 | 12 | 24 | 5.3 | 2.3 |
| 16 | 256 | 240 | 32 | 64 | 8 | 3.75 |
| 32 | 1024 | 992 | 80 | 160 | 12.8 | 6.2 |
| 64 | 4096 | 4032 | 192 | 384 | 21.3 | 10.5 |
| 128 | 16384 | 16256 | 448 | 896 | 36.6 | 18.1 |
| . | . | . | . | . | . | . |
| 4096 | 16777216 | 16773120 | 24576 | 49152 | 683 | 341 |
| 8192 | 67108864 | 67100672 | 53248 | 106496 | 1260 | 630 |
Как видно, чем больше длина преобразования, тем больше экономия вычислительных ресурсов (по скорости обработки или количеству аппаратных блоков)!
Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые называются *гармоники*. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте. Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.
Свертка и корреляция
В этом разделе вводится понятие корреляции и свертки для дискретных случайных и детерминированных последовательностей. Показана связь автокорреляционной и взаимнокорреляционной функций со сверткой. Описываются свойства свертки, в частности, рассмотрены методы линейной и циклической свертки дискретного сигнала с подробным разбором на примере дискретной последовательности. Кроме того, показан метод вычисления «быстрой» свертки с помощью алгоритмов БПФ.
В реальных задачах часто ставится вопрос о степени похожести одного процесса на другой или же о независимости одного процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию. Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме того, с помощью корреляции производится поиск слабых сигналов в шумах.
Свертка описывает взаимодействие сигналов между собой. Если один из сигналов — импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное воздействие. Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.
Автокорреляционная функция (АКФ) находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых последовательностей).
В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле (по числу вещественных умножений).
Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает выигрывать у прямого метода. Очевидно, чем больше длина БПФ, тем лучше выигрыш частотного метода.
| N | Свертка | Быстрая свертка | Отношение |
|---|---|---|---|
| 8 | 64 | 448 | 0.14 |
| 16 | 256 | 1088 | 0.24 |
| 32 | 1024 | 2560 | 0.4 |
| 64 | 4096 | 5888 | 0.7 |
| 128 | 16K | 13312 | 1.23 |
| . | . | .. | . |
| 2048 | 4M | 311296 | 13.5 |
Случайные сигналы и шум
В этом разделе вводится понятие случайных сигналов, плотности распределения вероятностей, закона распределения случайной величины. Рассматриваются математические моменты — среднее (математическое ожидание) и дисперсия (или корень этой величины — среднеквадратическое отклонение). Также в этом разделе рассматривается нормальное распределение и связанное с ним понятие белого шума, как основного источника шумов (помех) при обработке сигналов.
Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. К основным характеристикам случайных сигналов относятся:
В задачах ЦОС случайные сигналы делятся на два класса:
С помощью случайных величин можно моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. При прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило, спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный белый гауссовский шум (AWGN — Additive white Gaussian noise).
Сигналы, модуляция и манипуляция
В этом разделе показаны основные способы изменения одного или нескольких параметров гармонического сигнала. Вводятся понятия амплитудной, частотной и фазовой модуляции. В частности, выделяется линейная частотная модуляция, применяемая в задачах радиолокации. Показаны основные характеристики сигналов, спектры модулированных сигналов в зависимости от параметров модуляции.
Для удобства на языке Python создан набор функций, осуществляющих перечисленные виды модуляции. Пример реализации ЛЧМ-сигнала:
Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции — манипуляции. Как и в случае с аналоговыми сигналами, цифровые гармонические последовательности могут быть манипулированы по амплитуде, фазе и частоте (либо по нескольким параметрам сразу).
Цифровые фильтры — БИХ и КИХ
Достаточно большой раздел, посвященный вопросам цифровой фильтрации дискретных последовательностей. В задачах цифровой обработки сигналов данные проходят через цепи, которые называются фильтрами. Цифровые фильтры, как и аналоговые, обладают различными характеристиками — частотные: АЧХ, ФЧХ, временная: импульсная характеристика, а также передаточная характеристика фильтра. Цифровые фильтры используются в основном для улучшения качества сигнала — для выделения сигнала из последовательности данных, либо для ухудшения нежелательных сигналов — для подавления определенных сигналов в приходящих последовательностях отсчетов.
В разделе перечислены основные преимущества и недостатки цифровых фильтров (в сравнении с аналоговыми). Вводится понятие импульсной и передаточной характеристик фильтра. Рассматривается два класса фильтров — с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Показан способ проектирования фильтров по канонической и прямой форме. Для КИХ фильтров рассматривается вопрос о способе перехода к рекурсивной форме.
Для КИХ фильтров показан процесс проектирования фильтра от стадии разработки технического задания (с указанием основных параметров), до программной и аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления числа, разрядности данных и т.д.). Вводятся определения симметричных КИХ фильтров, линейной ФЧХ и её связи с понятием групповой задержки.
Оконные функции в задачах фильтрации
Чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра и наоборот.
Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — **треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера** и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных устройствах (программируемые логические схемы или сигнальные процессоры).
Ресемплинг. Децимация и интерполяция
В этом разделе рассматриваются вопросы многоскоростной обработки сигналов — изменения частоты дискретизации. Многоскоростная обработка сигналов (multirate processing) предполагает, что в процессе линейного преобразования цифровых сигналов возможно изменение частоты дискретизации в сторону уменьшения или увеличения, либо в дробное число раз. Это приводит к более эффективной обработке сигналов, так как открывается возможность использования минимально допустимых частот дискретизации и, как следствие, значительного уменьшения требуемой вычислительной производительности проектируемой цифровой системы.
Децимация (прореживание) – понижение частоты дискретизации. Интерполяция – повышение частоты дискретизации.
Также в разделе рассматривается класс однородных КИХ фильтров, которые называются интегрально-гребенчатыми фильтрами (CIC, Cascaded integrator–comb). Показана реализация, основные свойства и особенности CIC фильтров. В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд, что дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает «завал» главного лепестка амплитудно-частотной характеристики.
График АЧХ фильтра в зависимости от коэффициента децимации:
Также в этом разделе обсуждается вопрос увеличения разрядности данных на выходе CIC фильтра в зависимости от его параметров. Это особенно важно в задачах программной реализации, в частности на ПЛИС.
Для практической реализации CIC фильтров на Python разработан отдельный класс CicFilter, реализующий методы децимации и интерполяции. Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из scipy пакета Python.
Наконец, в этом разделе приведен особый класс фильтров — скользящего среднего. Показано три способа реализации: через свертку сигналов, с помощью КИХ-фильтра и БИХ-фильтра.
Заключение
Надеюсь, этот курс лекций в совокупности с моими предыдущими статьями по цифровой обработке сигналов на ПЛИС принесет практическую пользу и поможет читателю лучше понять основы цифровой обработки сигналов. Этот проект будет улучшаться и дополняться новым полезным и не менее интересным материалом. Следите за развитием!
Дополнительно к этому материалу я поддерживаю и развиваю свой проект по основным модулям ЦОС (на языке Python). Он содержит пакет генерации различных сигналов, класс CIC фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм вычисления сверх-длинного БПФ через методы двумерного преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).
UPD: 20.04.2020
Значение слова «децимация»
Децимация (обработка сигналов) — уменьшение частоты дискретизации сигнала.
децима́ция
1. истор. казнь каждого десятого (по жребию); мера наказания, применявшаяся в Древнем Риме и некоторых других государствах за совершение воинских (массовое бегство с поля боя) и некоторых других преступлений (бунт рабов)
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: двуручный — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «децимация»
Предложения со словом «децимация»
Понятия со словом «децимация»
Отправить комментарий
Дополнительно
Предложения со словом «децимация»
Заметим, что знавшие толк в военном искусстве римляне наказывали не только руководителя побежавшего с поля брани легиона, но и проводили децимацию (казнь каждого десятого) рядовых бойцов и младших командиров.
Он применил децимацию – казнил каждого десятого из беглецов.
Из всех провинившихся солдат по жребию отбирали примерно каждого десятого, которого забивали насмерть палками и камнями, – это называлось децимацией.
Децимация
 | Список значений слова или словосочетания со ссылками на соответствующие статьи. Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью. |
Смотреть что такое «Децимация» в других словарях:
ДЕЦИМАЦИЯ — (латинск. decimatio). Казнь каждого 10 го человека. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. децимация (лат. decimatio) 1) в древности казнь одного из 10 человек по жребию; 2) позже наказание каждого… … Словарь иностранных слов русского языка
децимация — прореживание; наказание, казнь Словарь русских синонимов. децимация сущ., кол во синонимов: 2 • казнь (27) • … Словарь синонимов
ДЕЦИМАЦИЯ — казнь каждого десятого (по жребию). Мера наказания, применявшаяся в Древнем Риме и некоторых других государствах за совершение воинских (массовое бегство с поля боя) и некоторых других преступлений (бунт рабов). Эта мера была известна и русскому… … Юридический словарь
децимация — и, ж. décimation f. < decimus десятый. юр., ист. Наказание каждого десятого в случае ненахождения виновного. Крысин 1998. Лекс. СИС 1954: децима/ция … Исторический словарь галлицизмов русского языка
децимация — Вычисление через определённые интервалы (каждое десятое значение) [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN decimation … Справочник технического переводчика
Децимация — (лат. decimatio) в армии Др. Рима казнь одного из 10 человек по жребию в наказание за трусость или невыполнение приказа всем подразделением; термин «Д.» в России употреблялся также в написании «децималия». Как вид наказания Д. широко применялась… … Энциклопедия права
децимация — децимация, децимации, децимации, децимаций, децимации, децимациям, децимацию, децимации, децимацией, децимациею, децимациями, децимации, децимациях (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
Децимация — (от лат. decimus десятый) в римской армии казнь каждого десятого воина, как наказание за невыполнение приказа или трусость, проявленную всем подразделением. (И.А. Лисовый, К.А. Ревяко. Античный мир в терминах, именах и названиях: Словарь… … Античный мир. Словарь-справочник.
децимация — казнь каждого десятого (по жребию). Мера наказания, применявшаяся в Древнем Риме и некоторых других государствах за совершение воинских (массовое бегство с поля боя) и некоторых других преступлений (бунт рабов). Эта мера была известна и русскому… … Большой юридический словарь
децимация — децим ация, и … Русский орфографический словарь
ДЕЦИМАЦИЯ И ИНТЕРПОЛЯЦИЯ ЦИФРОВЫХ СИГНАЛОВ
Применительно к цифровым сигналам децимация – уменьшение частоты дискретизации данных с сохранением в новом сигнале всей полезной информации. Интерполяция обратна децимации – увеличение частоты дискретизации также без изменения информации. Цифровая децимация и интерполяция широко используется в современных системах обработки данных с различными ширинами полос и частотами дискретизации, для сжатия и восстановления данных, для уменьшения объемов памяти хранения данных, для увеличения скорости передачи данных, для увеличения производительности систем с обработкой данных на разных скоростях, и т.п. Так, например, реализация узкополосных цифровых КИХ-фильтров требует очень большого числа коэффициентов, и децимация данных может существенно снизить размер фильтра и повысить скорость их обработки.
Простой, но мало производительный подход, к тому же не гарантирующий от внесения дополнительных ошибок – восстановить сигнал в аналоговой форме (ЦАП) и заново оцифровать его (АЦП) с новой частотой дискретизации. Цифровые методы позволяют выполнить эту операцию в более эффективной форме.
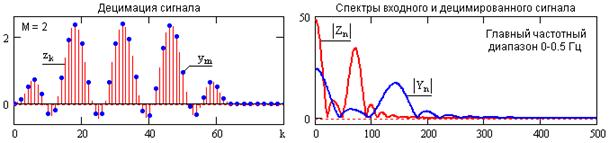
Децимация с целым шагом. Кратная компрессия частоты дискретизации снижает частоту дискретизации входного сигнала x(k) с fd до fd/M путем отбрасывания М-1 отсчетов в каждой последовательной серии из М-отсчетов, т.е. из М-отсчетов оставляется только 1:
Естественно, что частота Найквиста fN входного сигнала x(k) компрессора для выходного сигнала y(k) также уменьшается в М раз и становится равной fN‘ = fN/M для выходного сигнала. Соответственно, для полного сохранения после компрессии полезной информации, содержащейся в сигнале x(k), максимальная частота полезной информации во входном сигнале не должна превышать значения fmax £ fN/2M. В противном случае децимация будет некорректной и в новом главном частотном диапазоне выходного сигнала произойдет искажение спектра полезной информации за счет сложения со спектрами боковых диапазонов. Пример корректной децимации сигнала с М=2 и спектры входного и децимированного сигнала приведены на рис. 14.5.1.
Входные сигналы кроме полезной информации могут содержать статистические шумы и помехи, распределенные по всему частотному диапазону. При децимации шумы и помехи в частотном диапазоне от fN/M до fN входного сигнала зеркально отражаются от fN‘ нового главного частотного диапазона и их суммирование со спектром нового главного диапазона и полезного сигнала может приводить к увеличению уровня шумов и искажению информации. Для исключения этого эффекта перед конверсией сигнала необходимо выполнять его низкочастотную фильтрацию со срезом на частоте fN/2M.
При выполнении децимации с большими значениями коэффициента М операцию рекомендуется выполнять последовательными блоками M = M1 M2 …, что снижает требования к частотным характеристикам фильтров нижних частот.
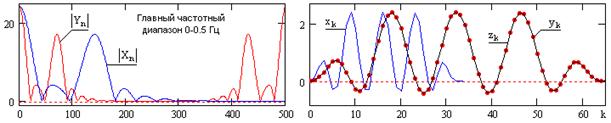
Интерполяция с целым шагом. Экспандер частоты дискретизации увеличивает частоту дискретизации входного сигнала xk с fd до Lfd путем введения (L-1) нулевых отсчетов после каждого отсчета входного сигнала. При этом форма спектра выходного сигнала yk остается без изменения, но частотная шкала спектра сжимается в L раз и в границы главного диапазона спектра входного сигнала ±fN заходят боковые диапазоны спектра выходного сигнала (зеркальные частоты). Это наглядно можно видеть на рис. 14.5.3 сравнением спектров Xn для входного сигнала xk, и Yn для экспандированного сигнала xk с L=2. Следовательно, фактическая частота Найквиста выходного сигнала становится равной fN/L. Для исключения зеркальных частот и распределения энергии отсчетов xk по L выходным интервалам экспандированный сигнал пропускается через фильтр нижних частот со срезом на частоте fN/L и с коэффициентом L для компенсации распределения энергии отсчетов по интервалам L. Результат операции можно видеть на сигнале yk по сравнению с исходным сигналом zk (рис. 14.5.1), децимацией которого с М=2 был получен сигнал xk.
При выполнении интерполяции с большим значением коэффициента L также рекомендуется выполнять операцию последовательными блоками L=L1 L2 … для снижения требований к частотным характеристикам фильтров низких частот.
Преобразование частоты дискретизации с нецелым шагом на практике обычно выполняют представлением нецелого множителя максимально близким приближением рациональными числами вида L/M, Это позволяет выполнять преобразование частоты дискретизации последовательными операциями сначала интерполяции с шагом L, сохраняющей все частотные составляющие сигнала, и затем децимации с шагом М, при которой часть высокочастотных составляющих и шумов будет подавлена низкочастотной фильтрацией. Поскольку при этом низкочастотные фильтры экспандирования и децимации следуют друг за другом и работают на одной частоте дискретизации, то вместо двух фильтров можно применять один, имеющий минимальную частоту среза с коэффициентом усиления, равным L.
При программной обработке больших пакетов данных децимация и интерполяция может выполняться в спектральной области с использованием БПФ.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет