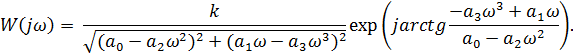диаграмма найквиста что это

График Найквиста

Амплитудно-фазовая частотная характеристика (АФЧХ) — удобное представление частотного отклика линейной стационарной динамической системы в виде графика в полярных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики. По сути такой график объединяет на одной плоскости амплитудно-частотную и фазо-частотную характеристики.

Термин употребляется также в применении к передаточной функции системы, записанной в виде преобразования Фурье выходного сигнала, поделённого на преобразование Фурье входного сигнала.

Содержание

Названия

В русской литературе для графика принято название АФЧХ (или АФХ). На западе АФЧХ называют диаграммой Найквиста или графиком Найквиста(англ. Nyquist Plot ), по имени выдающегося инженера Гарри Найквиста. Если же термин АФЧХ используется в применении к передаточной функции системы, его называют частотным откликом (англ. frequency response ).

Применения

АФЧХ применяется в основном для анализа систем, в частности исследования системы на устойчивость и её запасов.

АФЧХ является классическим средством анализа устойчивости линейных систем. Существует множество программных продуктов, позволяющих проводить исследования на устойчивость частотными методами.

АФЧХ типовых динамических звеньев

Измерение АФЧХ реальных линейных объектов

См. также

Полезное

Смотреть что такое «График Найквиста» в других словарях:

График (значения) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия

График (знач.) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия

АФЧХ — Запрос «График Найквиста» перенаправляется сюда; для значений термина «График» см. График. Запрос «Диаграмма Найквиста» перенаправляется сюда; для значений термина «Диаграмма» см. Диаграмма. Амплитудно фазовая частотная характеристика (АФЧХ)… … Википедия

Найквист, Гарри — Гарри Найквист (правильнее Никвист, англ. Harry Nyquist; 7 февраля 1889, Нильсби, Швеция 4 апреля 1976, Фарр, Техас) один из пионеров теории информации. Биография Гарри (Харри) Найквист родился в Нильсби, Швеция. Он иммигрировал… … Википедия

Найквист — Найквист, Гарри Гарри Найквист (англ. Harry Nyquist; 7 февраля 1889, Нильсби, Швеция 4 апреля 1976, Фарр, Техас) один из пионеров теории информации. Биография Гарри (Харри) Найквист родился в Нильсби, Швеция. Он иммигрировал в США в… … Википедия

Найквист Г. — Гарри Найквист (англ. Harry Nyquist; 7 февраля 1889, Нильсби, Швеция 4 апреля 1976, Фарр, Техас) один из пионеров теории информации. Биография Гарри (Харри) Найквист родился в Нильсби, Швеция. Он иммигрировал в США в 1907 году и поступил в… … Википедия

Найквист Гарри — Гарри Найквист (англ. Harry Nyquist; 7 февраля 1889, Нильсби, Швеция 4 апреля 1976, Фарр, Техас) один из пионеров теории информации. Биография Гарри (Харри) Найквист родился в Нильсби, Швеция. Он иммигрировал в США в 1907 году и поступил в… … Википедия

Частотная характеристика — Амплитудно фазовая частотная характеристика (АФЧХ) удобное представление частотного отклика линейной стационарной динамической системы в виде графика в полярных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и… … Википедия

Интерполяционная формула Уиттакера-Шеннона — служит для восстановления непрерывного сигнала с ограниченным спектром из последовательности равноотстоящих отсчетов. Интерполяционная формула, как ее обычно называют, восходит к работе Эмиля Бореля датированной 1898 годом, и к работе… … Википедия

Источник

3. Частотные характеристики систем автоматического управления (АФЧХ, ЛАХ, ФЧХ) ч. 3.1

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В этом разделе мы будем изучать частотные характеристики. Тема сегодняшней статьи:
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ

Будет интересно, познавательно и жестко.

3.1. Амплитудно-фазовая частотная характеристика: годограф АФЧХ, ЛАХ, ФЧХ

Определение: Частотными характеристиками называются формулы и графики, характеризующие реакцию звена (системы) на единичное синусоидальное воздействие в установившемся режиме, т.е. в режиме вынужденных гармонических колебаний звена (системы).

Формула синусоидального воздействия может быть записана как:

— сдвиг фазы (нередко называют — фаза);
— амплитуда;
т.е. амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия x(t).

Используем показательную форму записи функции единичного гармонического воздействия и отклика на это воздействие (рис. 3.1.1):

Определим связь между передаточной функцией и гармоничным воздействием, пользуясь показательной формой.
Рассмотрим звено уравнение динамики которого имеет следующий вид:

В показательной форме:

Запишем в показательной форме используя соотношения 3.1.1:

Подставим эти соотношения в (3.1.1) получим:

Поскольку (амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия), то можно записать:

если вспомнить, что в преобразования Лапласа , то:

Получаем выражение для передаточной функции

— Амплитудно-фазовая частотная характеристика (АФЧХ)
Иногда называют частотной передаточной функцией.
Модуль АФЧХ= тождественно равен амплитуде выходного сигнала:

Сдвиг фазы выходного сигнала:

Обычно АФЧХ изображается на комплексной плоскости. Формулы (3.1.6) и (3.1.7) позволяют изобразить в полярных координатах
Так же можно изображать в традиционных декартовых координатах:

Если использовать для представления W(s) форму W(s)=K·N(s)/L(s), где L(s)- полиномы по степеням s, (причем свободные члены равны 1), а К – общий коэффициент усиления звена (системы), то

Сдвиг фазы можно определить по виду многочленов и (см. формулу (3.1.9)) т.е. как разность фаз (аргументов) числителя и знаменателя:

Постоим АФЧХ для «абстрактного» звена (системы) с передаточной функцией:

Подставляя в формулу различные значения , получаем набор векторов, на комплексной плоскости

Рассмотрим действительную и мнимую части полученных векторов Из рисунка 3.1.3 видно, что:

Амплитуда и сдвиг фазы рассчитываются для векторов, соответствующих положительным частотам и лежащих в 4 квадранте по формулам:

В общем случае для любых углов сдвига необходимо учитывать переход между квадрантами на плоскости. Тогда формула принимает вид:

где:
j = 0, 2, 3, 4. если вектор в I и IV квадрант;
j = 1, 3, 4, 4. если вектор в II и III квадранте.

Во всех технических системах отклик системы, как правило, отстает от входного воздействия, то есть сдвиг фазы всегда отрицательный. Исходя из формулы 3.1.10, степень полинома L(s) выше, чем полинома N(s). Поскольку обычно степень полинома L(s) выше, чем полинома N(s), то с увеличением частоты на входе в звено (в систему) сдвиг фазы обычно отрицателен, т.е. сигнал на выходе звена еще больше отстает по фазе от входного сигнала при увеличении частоты.
В предельном случае, если частота растет до бесконечности, мы можем вообще не получить выходного воздействия. Обычно при ω→ ∞ величина амплитуды на выходе звена стремится к 0, то есть lim A(ω→∞) = 0.

при замене на имеет зеркальное изображение.

Анализируя годографы АФЧХ при > 0 (сплошная линия на рисунке 3.1.3) и при Рисунок 3.1.4 – «Зеркальная» симметрия относительно оси ординат.

Кроме анализа свойств звена (системы) по годографу АФЧХ, широкое распространение получили анализ логарифмической амплитудной характеристики (ЛАХ) и фазочастотной характеристики (ФЧХ).

ЛАХ определяется как Lm(ω)=20lgA(ω).

Поскольку зачастую удобнее использовать десятичные логарифмы (lg), чем натуральные(ln), в теории управления (также и в акустике) значительно чаще используется специальная единица – децибел (1/10 часть Бела):
+1Бел – единица, характеризующая увеличение в 10 раз.
+1дБ (децибел) – соответствует увеличению в раз.

В формуле Lm(ω)=20lgA(ω) величина Lm(ω) измеряется также в децибелах. Происхождение множителя 20 таково: A(ω) – амплитуда, линейная величина, а мощность — квадратичная величина (например, напряжение в сети измеряется в Вольтах, а мощность () пропорциональна квадрату напряжения, поэтому в формуле для Lm(ω) стоит множитель 20 (чтобы привести ЛАХ (Lm(ω)) к традиционной мощностной характеристике).

Если больше на 20 дБ, то это означает, амплитуда больше амплитуды в 10 раз,

Окончательно: Lm(ω)=20lg│W(iω)│= 20lgA(ω)

Графики A(ω) и φ(ω) имеют вид:

Учитывая, что “ω” обычно изменяется на порядки и значение A(ω) – также на порядки, график Lm(ω) строится, фактически, в логарифмических координатах, т.е. Lm(ω) =Lm(lg(ω)), например:

Наклон (– 40 дБ/дек) соответствует уменьшению амплитуды в 100 раз при увеличении частоты в 10 раз.

Рассмотренные характеристики Lm(ω), то есть ЛАХ и ФЧХ имеют широкое распространение при анализе динамических свойств звена (системы), например, при анализе устойчивости САР (см. раздел “Устойчивость систем автоматического управления”).

Рисунок 3.1.10 – пример ЛАХ и ФЧХ для сложной системы

Пример 1

Параметры блока «Построение частотных характеристик» приведены на рисунке 3.1.12, для иллюстрации зависимости АЧХ и ЛАХ. Результат работы блока — график с выбранными параметрами — изображен на рисунке 3.1.13:

Анализ графика в линейном масштабе по ω чаще всего не очень удобен, поскольку весь график собирается в узкой области, а дальше график абсолютной амплитуды практически сливается с 0. Если мы хотим исследовать частоты хотя бы до 1000 Гц, мы увидим практически вертикальные и горизонтальные прямые. Изменения масштаба шкалы АЧХ и ω на логарифмический дает возможность лучше исследовать частотные характеристики (см. рис. 3.1.14).

На рисунке 3.1.14 представлены частотные характеристики демпфера в логарифмическом масштабе и иллюстрация соотношения между абсолютной величиной амплитуды АФЧХ и ЛАХ в децибелах.

Пример 2

Постоим частотные характеристики для чуть более сложной модели, а именно — для гидравлического демпфера, рассмотренного в предыдущей лекции.

Для начала посмотрим на модель в виде блоков.

Модель, подготовленная для анализа, представлена на рисунке 3.1.15. В отличие от исходной модели, описанной ранее, входное воздействие задается блоком «ступенька» с скачком с 0 до 1 на 10 секунде расчёта. В блоке «линейная функция» происходит пересчет сигнала «ступенька»:
0 — соответствует 200 бар в камере (конечное состояние в предыдущем примере)
1 — соответствует 400 бар в камере.
Это сделано для того, чтобы можно было подавать синусоидальный сигнал и не получать отрицательное давление в камере плунжера. Также для наглядности графика мы усиливаем выходное перемещение, переводя его из метров в миллиметры.

Частотные характеристики, получаемые в конце расчёта, приведены на рисунке 3.1.16. Видно что характеристики отличаются от простого пружинного демпфера (сравните с 3.1.14)

Блок «Построение частотных характеристик» осуществляет расчет характеристик для линеаризованной модели в окрестности заданной точки. Это означает, что частотные характеристики системы в разные моменты времени могут отличаться для нелинейных моделей. Например, в нашем случае характеристики в начале расчёта будут отличаться от характеристик, полученных в конце расчёта.

Для подробных и нелинейных моделей, блок «Построение частотных характеристик» может не работать из за наличия разрывов и нелинейностей в модели. Как например, для «точной» модели демпфера, которую мы проверяли в предыдущей статье. В этом случае возможно построить частотные характеристики непосредственно моделированием, путем подачи синусоидального сигнала с разной частотой и измерения отклика. В SimInTech для этого используется блок «Гармонический анализатор», который подключается ко входу модели и генерирует синусоидальное воздействие. В этот же блок направляется отклик системы, и производится вычисление необходимых параметров для построения различных характеристик системы, которые можно вывести на графики с помощью блока «фазовый портрет».

Модель гидравлического демпфера, собранного из библиотечных блоков SimInTech, представлена на рисунке 3.1.7

Расчеты с моделью показывают, что при сохранении общего вида графиков значения, полученные для «подробной модели», отличаются от линеаризованной модели (см. рис. 3.18 — 3.19)

Использование прямого моделирования для получения характеристик является более надежным способом и работает не только с линейными моделями, но также может быть применимо для построения характеристик некоторых реальных объектов, если их можно подключить к среде моделирования и воздействовать в реальном режиме времени. Однако затраты на вычисления значительно будут больше. Например, для получения характеристик демпфера пришлось выполнить процесс в 40 000 секунд модельного времени, на обычном компьютере это заняло порядка 35 минут. График процесса перемещения плунжера в процессе вычисления характеристик приведен на рисунке 3.1.20.

Блок «Гармонический анализатор» имеет выходы:
Re(w*t) – текущее значение действительной части амплитудно-фазовой частотной характеристики исследуемой системы;
Im(w*t) – текущее значение мнимой части амплитудно-фазовой частотной характеристики.
Это позволяет построить годограф исследуемой системы с помощью фазового портрета. (см. рис. 3.1.21)

Модели, использованные для иллюстрации в лекции можно взять здесь…

Источник

Критерий устойчивости Найквиста

И Найквиста.

С помощью этих критериев исследуется устойчивость САР в частотой области.

Частотный критерий Михайлова

Исходная информация – характеристическое уравнение разомкнутой или замкнутой системы

Путём замены s на jw переходим к уравнению Михайлов

где Р(w) – вещественная часть годографа Михайлова, чётная функция частоты; Q (w) – мнимая часть годографа Михайлова, нечётная функция частоты.

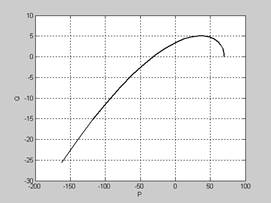
Критерий Михайлова формулируется следующим образом: система устойчива, если годограф Михайлова при изменении w от 0 до ¥ проходит в положительном направлении n квадрантов комплексной плоскости, начиная свое движение с точки а₀ положительной полуоси, и нигде не обращается в нуль.

Критерий Михайлова имеет и другую формулировку: система устойчива, если действительная и мнимая части годографа Михайлова обращаются в нуль поочерёдно, т.е. если корни уравнений

действительные и перемежаются, при w = 0 P(0) > 0, Q(0) > 0.

Пример: определить устойчивость системы, характеристическое уравнение которой

D(p) = 0,0057s 3 + 0,58s 2 + s + 70.

Выполним подстановку s = jw и выделим вещественную и мнимую части годографа Михайлова

Для ряда значений частоты w вычислим вещественную

мнимую части кривой Михайлова

и результаты расчётов сведём в таблицу, по данным которой можно построить кривую Михайлова. Для определения точек пересечения осей нужно решить уравнения Р(ω) = 0 и Q(ω) = 0. Однако целесообразно для построения графика использовать возможности MATLAB:

Кривая Михайлова последовательно проходит три квадранта. Так как характеристическое уравнение исследуемой системы третьего порядка, то система устойчива.

Различные виды годографов представлены на рис. 6.4. Системе, находящейся на границе устойчивости, соответствует годограф, проходящий через начало координат, неустойчивой системе – кривая, проходящая через 1, 4 и 3 квадранты.

Критерий устойчивости Найквиста

Это также частотный критерий, позволяющий судить об устойчивости системы, замкнутой единичной отрицательной обратной связью, по амплитудно-фазовой частотной характеристике разомкнутого контура. Предварительно требуется исследование устойчивости разомкнутой системы, как правило, по алгебраическим критериям. Для устойчивых и неустойчивых в разомкнутом состоянии систем формулировки критерия разные.

Для систем, неустойчивых в разомкнутых состояниях, критерий Найквиста имеет такую формулировку: если разомкнутая система неустойчива и имеет m корней в правой полуплоскости, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутого контура охватывала точку с координатами (-1, j0) m/2 раз.

Если система имеет местные обратные связи, то необходимо проверить устойчивость внутренних контуров любым критерием.

Пример: задана передаточная функция системы управления

Исследовать её на устойчивость.

Сделаем замену s = jω и найдём АФЧХ:

Диаграмма Найквиста может быть построена в MATLAB с помощью функции nyquist([…],[…]) или nyquist(W).

Пример: построить годограф Найквиста для системы с передаточной функцией

В соответствии с критерием Гурвица эта система устойчива в разомкнутом состоянии. Исследуем её устойчивость в замкнутом состоянии:

>> nyquist([5],[1 3 3 1]) – рис. 6.5

АФЧХ разомкнутой системы не охватывает точку с координатами

(-1, j0), поэтому замкнутая система устойчива.

6.4. Устойчивость систем с запаздыванием.

Отдельные звенья САР обладают “чистым” запаздыванием, которое сказывается в том, что система реагирует на входной сигнал не сразу, а по истечении некоторого постоянного времени t. Это обстоятельство учитывается введением звена чистого запаздывания с передаточной функцией

а структурная схема системы показана на рис. 6.6.

Передаточная функция разомкнутой системы

Система без запаздывания (t = 0) называется предельной.

Частотные характеристики системы с запаздыванием и без него определяются, соответственно, выражениями

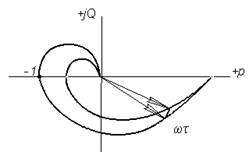
Отсюда видно, что для построения частотного годографа системы с запаздыванием следует построить годограф системы без запаздывания (предельной системы) и каждый вектор этого годографа повернуть по часовой стрелке на угол wt. Последний возрастает как при увеличении w, так и t.

Для некоторого значения t = t₀ и w = w_p годограф пройдёт через точку (-1, j0), и, следовательно, АСР будет находиться на границе устойчивости (рис. 6.7). Значения t₀ и w_p определяются из уравнения

Пример: система состоит из апериодического звена первого порядка с передаточным коэффициентом к > 1, постоянной времени Т и звена запаздывания с постоянной времени t. Определить предельное время запаздывания t₀, при котором система устойчива.

Источник