длина окружности что это
Длина окружности
6 класс, 9 класс, ЕГЭ/ОГЭ
Как найти длину окружности через диаметр
Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:
π— число пи — математическая константа, равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, равное 3,14
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, равное 3,14
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен 
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Длина окружности
Возьмем циркуль. Установим ножку циркуля с иглой в точку « O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
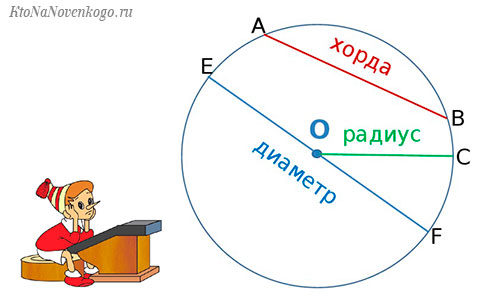
Диаметр окружности обозначается буквой « D ». На рисунке выше — это отрезок « BC ».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение « D = 2R ».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
π ≈ 3,14…
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2 π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Определите диаметр окружности, если её длина равна 56,52 дм. ( π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки « A » и « B ». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга « AB » и черная дуга « AB ». Точки « A » и « B » называют концами дуг.
Соединим точки « A » и « B » отрезком. Полученный отрезок называют хордой.
Точки « A » и « B » делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга « AB ».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.
Длина окружности
Длина окружности — это длина закрытой кривой. Определение окружности в статье Окружность.
Длина окружности вычисляется из диаметра по формуле::
Или из половины диаметра, радиуса:
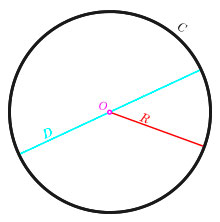
где r — это радиус, d — диаметр круга, а π (греческая буква пи), которая является математической постоянной, отношением длины окружности к ее диаметру (значение пи, первые цифры: 3.141 592 653 589 793).
Смотреть что такое «Длина окружности» в других словарях:
длина окружности резервуара — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN tank circumference … Справочник технического переводчика
длина окружности совокупность известных операций — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN circuit … Справочник технического переводчика
ДЛИНА — ДЛИНА, длины, мн. нет, жен. Протяжение линии, плоскости, тела в том направлении, в котором две крайние точки (линии, плоскости, тела) лежат на наибольшем расстоянии одна от другой. Предметы измеряются в длину, ширину и высоту. Длина стола. Меры… … Толковый словарь Ушакова
длина — ы/, только ед., ж. 1) Протяжение в том направлении, в котором две крайние точки линии, плоскости, тела лежат на наибольшем расстоянии друг от друга. Мера длины. Лыжи длиной в два метра. Измерить площадку в длину и в ширину. Синонимы: расстоя/ние… … Популярный словарь русского языка
Длина кривой — (или, что то же, длина дуги кривой) в метрическом пространстве числовая характеристика протяжённости этой кривой[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой… … Википедия
Длина шкалы — Расстояние между крайними отметками шкалы, отсчитанное по дуге окружности или по прямой линии, проходящей через середины наименьших отметок Источник: ГОСТ 2405 88: Манометры, вакуумметры, мановакуумметр … Словарь-справочник терминов нормативно-технической документации
Длина дуги — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия
Длина дуги кривой — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия
длина — 3.1 длина (length) l: Наибольший линейный размер лицевой грани измеряемого образца. Источник: ГОСТ Р ЕН 822 2008: Изделия теплоизоляционные, применяемые в строительстве. Методы измерения длины и ширины … Словарь-справочник терминов нормативно-технической документации
Длина — числовая характеристика протяжённости линий. В разных случаях понятие Д. определяется различно. 1) Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. 2) Д. ломаной сумма Д. её звеньев.… … Большая советская энциклопедия
Длина окружности
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня у нас очередная математическая тема. Ее проходят в 6-м классе. Называется она – ДЛИНА ОКРУЖНОСТИ.
Эта важная величина для решения многих задачек. В том числе и во время Единого госэкзамена.
Так что наша статья будет крайне полезна школьникам-выпускникам. А для всех остальных это хороший повод освежить свои знания.
Что такое окружность
Но для начала напомним, что называют окружностью.
Окружность – это кривая замкнутая линия, которая состоит из множества точек. И эти точки находятся на одном расстоянии от центра окружности.
Определение несколько «тяжеловатое», но это официальная формулировка, которая также приводится в школьных учебниках. Графически все выглядит гораздо проще.
Вот пример окружности, у которой все точки на кривой «С» равноудалены от центра «О».
Кстати, расстояние от центра до границы окружности называется радиус и обозначается он буквой «R».
А отрезок, который соединяет две точки на окружности и проходит через ее центр – это диаметр «D». И, как всем известно, диаметр – это два сложенных радиуса (D = 2R).
Интересный факт! Точка тоже является в некотором роде окружностью. В математике ее называют «окружностью нулевого радиуса».
А чтобы начертить правильную окружность, нужно воспользоваться специальным прибором – циркулем. Им же можно нарисовать и окружность нужного радиуса.
Длина окружности через диаметр
Зачем мы так подробно рассказали о самой окружности, ее радиусе и диаметре? Все просто – без них не обойтись при расчете длины окружности.
Эту зависимость заметили еще в Древнем Египте. Тогдашние математики были весьма продвинуты в различных инженерных расчетах. Достаточно вспомнить, насколько надежно построены пирамиды. Им более 5 тысяч лет, а кажется, что простоят еще столько же и даже больше.
Так вот, египтяне определили, что соотношение длины окружности и ее диаметра – величина постоянная.
Другими словами, если взять совершенно разные по размерам окружности, а потом поделить их длины на их же диаметры, то получится одно и то же число.
У египтян это было число 3. Но впоследствии было получено более точное значение, которое равно 22/7 или 3 целых и 1/7.
Так появилась математическая постоянная «ПИ». Сейчас это один из столпов науки, с помощью которого решаются многие задачи.
Кстати, само название «пи» происходит от греческого слова «περιφέρεια», что как раз переводится как окружность. А «περίμετρος» — это диаметр.
Этими обозначениями и воспользовался математик Леонард Эйлер, когда в 1737 году представил научному сообществу число «пи», обозначив его изначально буквой выше упомянутых слов.
И сейчас уже каждый школьник знает, что число «пи» равно 3,14. Это значение взято за базовое, хотя на самом деле в нем бесконечное количество знаков после запятой.
Формула длины окружности
Ну а теперь главный вывод из этого исторического экскурса. Согласно вычислениям еще древнеегипетских ученых, формула длины окружности выглядит так:
Но чаще всего эту формулу принято писать без знаков умножения:
Формула эта единственная. И других возможностей рассчитать длину окружности — нет. Хотя ее можно представить, как диаметр умноженный на ПИ, но это уже банальность.
Вот и все, что мы хотели рассказать по этой теме, а более подробно смотрите в приведенном видеоролике:
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Вот объясните, как длина окружности может иметь конечное значение, если её можно разбить на отрезки, а те отрезки на ещё меньшие отрезки и так до бесконечности. Как то, что состоит из бесконечного количества отрезков, может быть конечно?
Площадь круга и его частей. Длина окружности и ее дуг
 Основные определения и свойства. Число π Основные определения и свойства. Число π |
 Формулы для площади круга и его частей Формулы для площади круга и его частей |
 Формулы для длины окружности и ее дуг Формулы для длины окружности и ее дуг |
 Площадь круга Площадь круга |
 Длина окружности Длина окружности |
 Длина дуги Длина дуги |
 Площадь сектора Площадь сектора |
 Площадь сегмента Площадь сегмента |








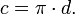
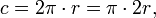



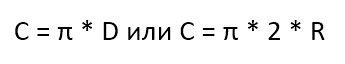
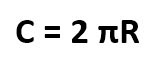










 ,
, ,
, ,
, ,
, ,
,


 ,
,




















