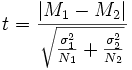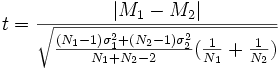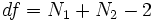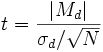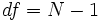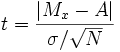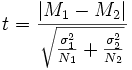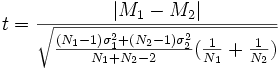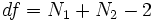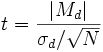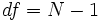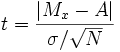для чего был впервые разработан t критерий стьюдента

T-критерий Стьюдента

t-критерий Стьюдента

Содержание

История

Данный критерий был разработан Уильямом Госсеттом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).

Требования к данным

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

Двухвыборочный t-критерий для независимых выборок

В случае с незначительно отличающимся размером выборки применяется упрощённая формула приближенных расчётов:

В случае, если размер выборки отличается значительно, применяется более сложная и точная формула:

Количество степеней свободы рассчитывается как

Двухвыборочный t-критерий для зависимых выборок

Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

Количество степеней свободы рассчитывается как

Одновыборочный t-критерий

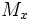
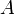
Применяется для проверки гипотезы об отличии среднего значения от некоторого известного значения :

Количество степеней свободы рассчитывается как

Непараметрические аналоги

Аналогом двухвыборочного критерия для независимых выборок является U-критерий Манна-Уитни. Для ситуации с зависимыми выборками аналогами являются критерий знаков и T-критерий Вилкоксона

Автоматический расчет t-критерия Стьюдента

Полезное

Смотреть что такое «T-критерий Стьюдента» в других словарях:

Критерий Стьюдента t-к — Критерий Стьюдента, t к. * крытэрый Ст’юдэнта, t к. * Student’s criterion or t c. or S. t test статистический критерий существенности разности между сравниваемыми средними. Определяется отношением этой разности к ошибке разности: При значениях t… … Генетика. Энциклопедический словарь

Критерий Стьюдента — t критерий Стьюдента общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t критерия связаны с проверкой равенства… … Википедия

критерий Стьюдента — Stjūdento kriterijus statusas T sritis augalininkystė apibrėžtis Skirtumo tarp dviejų vidurkių patikimumo rodiklis, išreiškiamas skirtumo ir jo paklaidos santykiu. atitikmenys: angl. Student’s test rus. критерий Стьюдента … Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas

критерий Стьюдента — Статистический критерий, в котором, в предположении нулевой гипотезы, используемая статистика соответствует t распределению (распределению Стьюдента). Примечание. Вот примеры применения этого критерия: 1. проверка равенства среднего из… … Словарь социологической статистики

КРИТЕРИЙ СТЬЮДЕНТА — Биометрический показатель достоверности разницы (td) между средними значениями двух сравниваемых между собой групп животных (M1 и М2) по какому либо признаку. Достоверность разницы определяется по формуле: Полученное значение td сравнивается с… … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных

КРИТЕРИЙ СТЬЮДЕНТА — оценивает близость двух средних значений с точки зрения отнесения или не отнесения ее к случайной (при заданном уровне значимости), отвечая на вопрос о том, отличаются ли средние значения статистически достоверно друг от друга [10, c. 98; 47, c.… … Современный образовательный процесс: основные понятия и термины

t-критерий Стьюдента — t критерий Стьюдента общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t критерия связаны с проверкой равенства средних… … Википедия

Критерий согласия Колмогорова — или Критерий согласия Колмогорова Смирнова статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.… … Википедия

критерий статистический — показатели, сочетающие в себе методы расчета, теоретическую модель распределения и правила принятия решения о правдоподобности нулевой или одной из альтернативных гипотез. Обычно делятся на параметрические, в коих предполагается обязательным… … Большая психологическая энциклопедия

Критерий Вальда — (максиминный критерий[1]) один из критериев принятия решений в условиях неопределённости. Критерий крайнего пессимизма. История Критерий Вальда был предложен Абрахамом Вальдом в 1955 году для выборок равного объема, а затем распространен на … Википедия

Источник

T-критерий стьюдента

Критерий Стьюдента был разработан английским химиком У. Госсетом. Публикации своих статей по t-критерию У. Госсет сделал в 1908г. в журнале Биометрика под псевдонимом Student, что в переводе означает Студент. В отечественной же литературе принято писать Стьюдент. Коварная простота вычисления t-критерия Стьюдента, а также его наличие в большинстве статистических пакетов и программ привели к широкому использованию этого критерия даже в тех условиях, когда применять его нельзя.

Наиболее часто t–критерий используется в двух случаях. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t–критерий). В этом случае есть контрольная группа и опытная группа, состоящая из разных пациентов, количество которых в группах может быть различно. Во втором же случае используется так называемый парный t–критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными. Например, измеряется содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения. В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп.

Критерий Стьюдента является наиболее часто используемым методом обнаружения различия между средними двух выборок. Например, t–критерий можно использовать для сравнения средних показателей группы пациентов, принимавших определенное лекарство, с контрольной группой, где принималось безвредное лекарство. Теоретически, t–критерий может применяться, даже если размеры выборок очень небольшие (например, 10; некоторые исследователи утверждают, что можно исследовать выборки меньшего размера), и если переменные нормально распределены (внутри групп), а дисперсии наблюдений в группах не слишком различны.

Предположение о нормальности можно проверить, исследуя распределение (например, визуально с помощью гистограммы) или применяя какой-либо критерий нормальности.

Чтобы применить t–критерий для независимых выборок, требуется, по крайней мере, одна независимая (группирующая) переменная (например, Пол: мужчина/женщина) и одна зависимая переменная (например, тестовое значение некоторого показателя, кровяное давление, число лейкоцитов и т.д.). С помощью специальных значений независимой переменной (эти значения называются кодами, например, мужчина и женщина) данные разбиваются на две группы.

На практике часто приходится сравнивать более двух групп данных (например, имеется лекарство 1, лекарство 2 и успокоительное лекарство) или сравнивать группы, созданные более чем одной независимой переменной (например, Пол, тип Лекарства и Доза). В таких более сложных исследованиях следует использовать дисперсионный анализ, который можно рассматривать как обобщение t–критерия.

Степень различия между средними в двух группах зависит от внутригрупповой вариации (дисперсии) переменных. В зависимости от того, насколько различны эти значения для каждой группы, грубая разность между групповыми средними показывает более сильную или более слабую степень зависимости между независимой (группирующей) и зависимой переменными. Например, если среднее значение числа лейкоцитов (WCC) равнялось 102 для мужчин и 104 для женщин, то разность внутригрупповых средних только на величину 2 будет чрезвычайно важной, когда все значения WCC мужчин лежат в интервале от 101 до 103, а все значения WCC женщин– в интервале 103– 105. В этом случае можно довольно хорошо предсказать WCC (значение зависимой переменной) исходя из пола субъекта (независимой переменной). Однако если та же разность 2 получена из сильно разбросанных данных (например, изменяющихся в пределах от 0 до 200), то этой разностью вполне можно пренебречь. Таким образом, можно сказать, что уменьшение внутригрупповой вариации увеличивает чувствительность критерия.

Критерий Стьюдента зависимых выборок очень полезен в тех довольно часто возникающих на практике ситуациях, когда важный источник внутригрупповой вариации (или ошибки) может быть легко определен и исключен из анализа. Например, это относится к экспериментам, в которых две сравниваемые группы основываются на одной и той же совокупности наблюдений (субъектов), которые тестировались дважды (например, до и после лечения, до и после приема лекарства). В подобных экспериментах значительная часть внутригрупповой изменчивости (вариации) в обеих группах может быть объяснена индивидуальными различиями субъектов.

Заметим, что на самом деле, такая ситуация не слишком отличается от той, когда сравниваемые группы совершенно независимы, где индивидуальные отличия также вносят вклад в дисперсию ошибки. Однако в случае независимых выборок, вы ничего не сможете поделать с этим, т.к. не сможете определить (или удалить) часть вариации, связанную с индивидуальными различиями субъектов. Если та же самая выборка тестируется дважды, то можно легко исключить эту часть вариации. Вместо исследования каждой группы отдельно и анализа исходных значений, можно рассматривать просто разности между двумя измерениями (например, до приема лекарства и после приема лекарства) для каждого субъекта. Вычитая первые значения из вторых (для каждого субъекта) и анализируя затем только эти чистые (парные) разности, вы исключите ту часть вариации, которая является результатом различия в исходных уровнях индивидуумов. Именно так и проводятся вычисления в t–критерии для зависимых выборок. В сравнении с t–критерием для независимых выборок, такой подход дает всегда лучший результат (критерий становится более чувствительным).

Т-критерий Стьюдента за 12 минут. Биостатистика.

Источник

t-критерий Стьюдента

Содержание

История

Требования к данным

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

Двухвыборочный t-критерий для независимых выборок

В случае с незначительно отличающимся размером выборки применяется упрощённая формула приближенных расчётов:

В случае, если размер выборки отличается значительно, применяется более сложная и точная формула:

Где — средние арифметические, — стандартные отклонения, а — размеры выборок.

Количество степеней свободы рассчитывается как

Двухвыборочный t-критерий для зависимых выборок

Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

где — средняя разность значений, а — стандартное отклонение разностей.

Количество степеней свободы рассчитывается как

Одновыборочный t-критерий

Применяется для проверки гипотезы об отличии среднего значения от некоторого известного значения :

Количество степеней свободы рассчитывается как

Непараметрические аналоги

Аналогом двухвыборочного критерия для независимых выборок является U-критерий Манна-Уитни. Для ситуации с зависимыми выборками аналогами являются критерий знаков и T-критерий Вилкоксона

Использование статистических пакетов

Analyze => Compare Means => Independent-Samples T-Test

Analyze => Compare Means => Paired-Samples T-Test

Analyze => Compare Means => One-Sample T-Test hu:Egymintás t-próba nl:T-toets

Источник

Математика, которая мне нравится

Математика для школьников и студентов, обучение и образование

Кто придумал t-критерий Стьюдента (Student)?

Стьюдент, ну кто же еще?

Конечно, многие ответили бы что-то вроде этого после прочтения названия. Собственно, вы правы, но кто был этот Стьюдент? В действительности Стьюдент — это не имя и не фамилия человека, изучавшего распределение вероятностей, это псевдоним. Настоящее имя создателя критерия Стьюдента Уильям Сили Госсет, и все, связанное с возникновением и использованием этого псевдонима, является довольно любопытной историей.

-распределение — это распределение вероятностей, связанное с нормальным распределением. Возникает оно, когда требуется оценить среднее статистической выборки, когда размер выборки, используемой для оценки, мал и дисперсии неизвестны. Определяется это распределение случайной величины следующим образом:

где , то есть нормальное распределение с математическим ожиданием и стандартным отклонением , — распределение хи-квадрат (еще одно распределение вероятностей, связанное с нормальным), — число степеней свободы распределения хи-квадрат.

История развития этого распределения вероятностей, как мы уже говорили в начале, весьма любопытна. Уильям Сили Госсет — английский математик и химик, который после окончания университета начал работать на заводе Guinness (да-да, знаменитого пива “Гиннесс’’), занимаясь контролем качества в процессе создания пива. Малый размер выборки, с которой обычно приходилось иметь дело, был виновником его занятий, которые в конечном счете привели к разработке -распределения. В 1908 году, когда ему было 32 года, Госсет опубликовал статью The probable error of a mean (“Вероятная ошибка среднего’’) в журнале Biometrika, но не под своим именем, а под псевдонимом Стьюдент.

Почему был избран псевдоним? Как это часто бывает в таких случаях, существует несколько теорий, пытающихся объяснить это. Первая и, видимо, наиболее распространенная, говорит, что основная причина в том, что Guinness ранее нес ущерб от утечки информации из-за публикаций сотрудников, что компания запретила своим сотрудникам публиковать статьи, независимо от их темы. Эта история имеет не одно продолжение, которое отличается в различных источниках. Некоторые говорят, что публикация Госсета под псевдонимом Стьюдент позволила скрыть от компании Guinness, что ее сотрудник опубликовал статью. Другие говорят, что Госсет договорился с пивоварней о ее публикации (однако содержание статьи не было бы полезно для конкуренции), но компания попросила использовать псевдоним, чтобы другие сотрудники не были осведомлены об этой публикации.

Вторая теория гласит, что псевдоним Стьюдент был использован для Гиннесса, потому что сама компания хотела сохранить в тайне статистика, работающего на нее. Это было сделано, чтобы не было никаких доказательств промышленного преимущества, достигнутого благодаря ему.

В любом случае, история использования псевдонима Стьюдент Уильямом Сили Госсетом, по меньшей мере, необычная, и в этом нет никаких сомнений.

Источник

Критерий Стьюдента

Содержание

История

Данный критерий был разработан Уильямом Госсеттом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (а руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсетта вышла в журнале «Биометрика» под псевдонимом «Student» (Студент).

Требования к данным

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

Двухвыборочный t-критерий для независимых выборок

В случае с незначительно отличающимся размером выборки применяется упрощённая формула приближенных расчётов:

В случае, если размер выборки отличается значительно, применяется более сложная и точная формула:

Количество степеней свободы рассчитывается как

Двухвыборочный t-критерий для зависимых выборок

Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

Количество степеней свободы рассчитывается как

Одновыборочный t-критерий

Применяется для проверки гипотезы об отличии среднего значения от некоторого известного значения :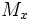

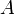
Количество степеней свободы рассчитывается как

Непараметрические аналоги

Аналогом двухвыборочного критерия для независимых выборок является U-критерий Манна-Уитни. Для ситуации с зависимыми выборками аналогами являются критерий знаков и T-критерий Вилкоксона

Полезное

Смотреть что такое «Критерий Стьюдента» в других словарях:

Критерий Стьюдента t-к — Критерий Стьюдента, t к. * крытэрый Ст’юдэнта, t к. * Student’s criterion or t c. or S. t test статистический критерий существенности разности между сравниваемыми средними. Определяется отношением этой разности к ошибке разности: При значениях t… … Генетика. Энциклопедический словарь

критерий Стьюдента — Stjūdento kriterijus statusas T sritis augalininkystė apibrėžtis Skirtumo tarp dviejų vidurkių patikimumo rodiklis, išreiškiamas skirtumo ir jo paklaidos santykiu. atitikmenys: angl. Student’s test rus. критерий Стьюдента … Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas

критерий Стьюдента — Статистический критерий, в котором, в предположении нулевой гипотезы, используемая статистика соответствует t распределению (распределению Стьюдента). Примечание. Вот примеры применения этого критерия: 1. проверка равенства среднего из… … Словарь социологической статистики

КРИТЕРИЙ СТЬЮДЕНТА — Биометрический показатель достоверности разницы (td) между средними значениями двух сравниваемых между собой групп животных (M1 и М2) по какому либо признаку. Достоверность разницы определяется по формуле: Полученное значение td сравнивается с… … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных

КРИТЕРИЙ СТЬЮДЕНТА — оценивает близость двух средних значений с точки зрения отнесения или не отнесения ее к случайной (при заданном уровне значимости), отвечая на вопрос о том, отличаются ли средние значения статистически достоверно друг от друга [10, c. 98; 47, c.… … Современный образовательный процесс: основные понятия и термины

T-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t критерия связаны с проверкой равенства средних значений в двух… … Википедия

t-критерий Стьюдента — t критерий Стьюдента общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t критерия связаны с проверкой равенства средних… … Википедия

Критерий согласия Колмогорова — или Критерий согласия Колмогорова Смирнова статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.… … Википедия

критерий статистический — показатели, сочетающие в себе методы расчета, теоретическую модель распределения и правила принятия решения о правдоподобности нулевой или одной из альтернативных гипотез. Обычно делятся на параметрические, в коих предполагается обязательным… … Большая психологическая энциклопедия

Критерий Вальда — (максиминный критерий[1]) один из критериев принятия решений в условиях неопределённости. Критерий крайнего пессимизма. История Критерий Вальда был предложен Абрахамом Вальдом в 1955 году для выборок равного объема, а затем распространен на … Википедия

Источник