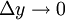для чего дифференцируют функцию
Дифференцируемость
Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.
Содержание
Определения
где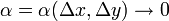 
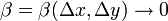
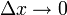
и 
при 
,
Свойства
Касательная прямая
Примеры
См. также
Ссылки
Полезное
Смотреть что такое «Дифференцируемость» в других словарях:
Дифференцируемость функции в точке — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
Непрерывная дифференцируемость — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
АППРОКСИМАТИВНАЯ ДИФФЕРЕНЦИРУЕМОСТЬ — обобщение понятия дифференцируемости с заменой обычного предела аппроксимативным пределом. Действительная функция действительного переменного наз. аппроксимативно дифференцируемой в точке х 0, если существует такое число А, что При этом величина… … Математическая энциклопедия
Аналитические функции — функции, которые могут быть представлены степенными рядами (См. Степенной ряд). Исключительная важность класса А. ф. определяется следующим. Во первых, этот класс достаточно широк; он охватывает большинство функций, встречающихся в… … Большая советская энциклопедия
Дифференцируемая функция — Дифференцируемая (в точке) функция это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является… … Википедия
Лобачевский, Николай Иванович — родился 22 октября 1793 г. в Нижегородской губернии (по одному источнику в Нижнем Новгороде, по другому в Макарьевском уезде). Отец его Иван Максимович, выходец из Западного края, по вероисповеданию католик, потом перешедший в православную веру,… … Большая биографическая энциклопедия
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия
Производная функции — У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная&# … Википедия
Голоморфная функция — осуществляет конформное отображение, преобразуя ортогональную сетку в ортогональную (там где комплексная производная не обращается в нуль). Голоморфная функция, также называемая регулярно … Википедия
Дифференцируемость
Оглавление
Действительные функции действительной переменной
Определения
Пояснения
Дифференцируемость следует за непрерывностью : каждая функция, которую можно дифференцировать в одной точке, также непрерывна там. Каждая функция, которую можно дифференцировать в своей области определения, непрерывна. Обратное неверно. Все перечисленные ниже недифференцируемые функции являются непрерывными.
Примеры дифференцируемых функций
Примеры недифференцируемых функций
Поскольку каждая дифференцируемая функция является непрерывной, наоборот, каждая разрывная функция (например, ступенчатая функция или функция Дирихле ) является примером недифференцируемой функции. Но есть также функции, которые непрерывны, но дифференцируемы не везде или не везде.
Корневая функция
Функция суммы
и левая производная
Это типичное поведение для функций, определенных в разделах, где значения функций совпадают на интерфейсах, но не производные. Напротив, графики дифференцируемых функций не имеют изломов.
Третий пример
непрерывна в точке 0, но не дифференцируема (но везде). Следующее относится к коэффициенту разницы в точке 0.
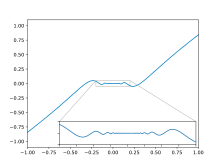
Функция Вейерштрасса
Функция Вейерштрассе названа в честь первооткрывателя
везде постоянна, но нигде не дифференцируема.
Винеровский процесс
Постоянная дифференцируемость и высшие производные
но не является непрерывным в 0.
Сложные функции
Действительные функции нескольких переменных
Частичная дифференцируемость
существует. Итак, вы рассматриваете все переменные, кроме как постоянные, и рассматриваете функцию переменной, полученную таким образом. Икс я <\ displaystyle x_ > 
Частичная дифференцируемость не приводит к непрерывности, а только в направлении осей координат.
Производная по направлению
Полная дифференцируемость
Полностью дифференцируемая функция также непрерывна.
В новейшей математической литературе в основном говорят просто о дифференцируемости, а не о полной дифференцируемости. Полная производная также называется дифференциалом.
Связь между различными концепциями дифференцируемости
Инверсии не применяются:
Другое дело, если допустить не только существование, но и непрерывность частных производных.
Поэтому непрерывно частично дифференцируемые функции называют просто непрерывно дифференцируемыми. Здесь тоже не действует обратное:
В целом применимо следующее:
непрерывная частичная дифференцируемость ⇒ полная дифференцируемость ⇒ дифференцируемость по каждому направлению ⇒ частичная дифференцируемость,
однако все обратное неверно.
Примеры
Контрпримеры
Частично дифференцируемые, но не непрерывные и не все производные по направлениям
частично дифференцируема и непрерывна в точке (0,0). Существуют все односторонние производные по направлениям, но кроме координатных направлений, а не двусторонних.
Односторонние, но не двусторонние направленные деривации
Предельное значение существует только с одной стороны, поэтому производные по направлению с обеих сторон не существуют. В частности, функция также не является частично дифференцируемой.
Все производные направления существуют, но не определяют линейное отображение
Здесь существуют все производные по направлениям, для которых применяются частные производные.
Все производные по направлениям существуют и определяют линейное отображение, но не полностью дифференцируемое.
— нулевое отображение, поэтому тривиально линейно.
Полностью дифференцируемый, но не непрерывно частично дифференцируемый
Эта функция моделируется на основе соответствующего примера функции переменной, проверка в основном такая же, как и там.
Отображения между конечномерными векторными пространствами
Функции и отображения в бесконечномерных векторных пространствах
Дифференцируемость по Гато
если предел существует.
Существует несколько несовместимых соглашений для термина дифференцируемость по Гато :
Дифференцируемость по Фреше
Подключения
Дифференцируемые отображения между дифференцируемыми многообразиями
Дифференцируемость образов между дифференцируемыми многообразиями объясняется дифференцируемостью их отображений. Здесь следует исходить из согласованности.
Аналогичным образом определяется комплексная дифференцируемость комплекснозначных функций на комплексных многообразиях и отображений между комплексными многообразиями.
Продление срока
Следующие понятия являются обобщениями дифференцируемости:
Для чего дифференцируют функцию
3.2.3. дЙЖЖЕТЕОГЙТХЕНПУФШ ЖХОЛГЙК. оЕРТЕТЩЧОПУФШ ДЙЖЖЕТЕОГЙТХЕНПК ЖХОЛГЙЙ
еУМЙ ЖХОЛГЙС ДЙЖЖЕТЕОГЙТХЕНБ Ч ЛБЦДПК ФПЮЛЕ ОЕЛПФПТПЗП ПФТЕЪЛБ [ Б ; b ] ЙМЙ ЙОФЕТЧБМБ ( Б ; b ), ФП ЗПЧПТСФ, ЮФП ПОБ ДЙЖЖЕТЕОГЙТХЕНБ ОБ ПФТЕЪЛЕ [ Б ; b ] ЙМЙ УППФЧЕФУФЧЕООП Ч ЙОФЕТЧБМЕ ( Б ; b ).
уРТБЧЕДМЙЧБ УМЕДХАЭБС ФЕПТЕНБ, ХУФБОБЧМЙЧБАЭБС УЧСЪШ НЕЦДХ ДЙЖЖЕТЕОГЙТХЕНЩНЙ Й ОЕРТЕТЩЧОЩНЙ ЖХОЛГЙСНЙ.
фБЛЙН ПВТБЪПН, ЙЪ ДЙЖЖЕТЕОГЙТХЕНПУФЙ ЖХОЛГЙЙ УМЕДХЕФ ЕЕ ОЕРТЕТЩЧОПУФШ.
еУМЙ 
, ФП 
ЗДЕ 
ВЕУЛПОЕЮОП НБМБС ЧЕМЙЮЙОБ, Ф.Е. ЧЕМЙЮЙОБ, УФТЕНСЭБСУС Л ОХМА РТЙ 
. оП ФПЗДБ
фБЛЙН ПВТБЪПН, Ч ФПЮЛБИ ТБЪТЩЧБ ЖХОЛГЙС ОЕ НПЦЕФ ЙНЕФШ РТПЙЪЧПДОПК. пВТБФОПЕ ХФЧЕТЦДЕОЙЕ ОЕЧЕТОП: УХЭЕУФЧХАФ ОЕРТЕТЩЧОЩЕ ЖХОЛГЙЙ, ЛПФПТЩЕ Ч ОЕЛПФПТЩИ ФПЮЛБИ ОЕ СЧМСАФУС ДЙЖЖЕТЕОГЙТХЕНЩНЙ (Ф.Е. ОЕ ЙНЕАФ Ч ЬФЙИ ФПЮЛБИ РТПЙЪЧПДОПК).
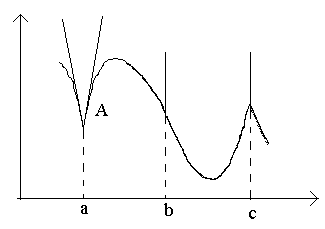
тБУУНПФТЙН ОБ ТЙУХОЛЕ ФПЮЛЙ Б, b, c.
ч ФПЮЛЕ b РТЙ ПФОПЫЕОЙЕ 
СЧМСЕФУС ЪОБЛПРПУФПСООПК ВЕУЛПОЕЮОП ВПМШЫПК ЧЕМЙЮЙОПК 
.
жХОЛГЙС ЙНЕЕФ ВЕУЛПОЕЮОХА РТПЙЪЧПДОХА. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ЧЕТФЙЛБМШОХА ЛБУБФЕМШОХА. фЙР ФПЮЛЙ – «ФПЮЛБ РЕТЕЗЙВБ» c ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК.
ч ФПЮЛЕ c ПДОПУФПТПООЙЕ РТПЙЪЧПДОЩЕ СЧМСАФУС ВЕУЛПОЕЮОП ВПМШЫЙНЙ ЧЕМЙЮЙОБНЙ ТБЪОЩИ ЪОБЛПЧ. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ДЧЕ УМЙЧЫЙЕУС ЧЕТФЙЛБМШОЩЕ ЛБУБФЕМШОЩЕ. фЙР – «ФПЮЛБ ЧПЪЧТБФБ» У ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК – ЮБУФОЩК УМХЮБК ХЗМПЧПК ФПЮЛЙ.
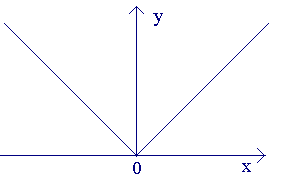
тБУУНПФТЙН ЖХОЛГЙА y=|x|.
ьФБ ЖХОЛГЙС ОЕРТЕТЩЧОБ Ч ФПЮЛЕ x = 0, Ф.Л. 
.
рПЛБЦЕН, ЮФП ПОБ ОЕ ЙНЕЕФ РТПЙЪЧПДОПК Ч ЬФПК ФПЮЛЕ.
оП ФПЗДБ РТЙ 
б РТЙ > 0
ф.П., ПФОПЫЕОЙЕ 
РТЙ 
УРТБЧБ Й УМЕЧБ ЙНЕЕФ ТБЪМЙЮОЩЕ РТЕДЕМЩ, Б ЬФП ЪОБЮЙФ, ЮФП ПФОПЫЕОЙЕ РТЕДЕМБ ОЕ ЙНЕЕФ, Ф.Е. РТПЙЪЧПДОБС ЖХОЛГЙЙ y=|x| Ч ФПЮЛЕ x = 0 ОЕ УХЭЕУФЧХЕФ. зЕПНЕФТЙЮЕУЛЙ ЬФП ЪОБЮЙФ, ЮФП Ч ФПЮЛЕ x = 0 ДБООБС «ЛТЙЧБС» ОЕ ЙНЕЕФ ПРТЕДЕМЕООПК ЛБУБФЕМШОПК (Ч ЬФПК ФПЮЛЕ ЙИ ДЧЕ).
Дифференцируемость функции в точке
Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.
Содержание
Определения
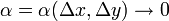
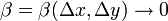
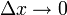
где и при ,
Свойства
Касательная прямая
Примеры
См. также
Ссылки
Полезное
Смотреть что такое «Дифференцируемость функции в точке» в других словарях:
Дифференцируемость — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
Аналитические функции — функции, которые могут быть представлены степенными рядами (См. Степенной ряд). Исключительная важность класса А. ф. определяется следующим. Во первых, этот класс достаточно широк; он охватывает большинство функций, встречающихся в… … Большая советская энциклопедия
Производная функции — У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная&# … Википедия
АППРОКСИМАТИВНАЯ ДИФФЕРЕНЦИРУЕМОСТЬ — обобщение понятия дифференцируемости с заменой обычного предела аппроксимативным пределом. Действительная функция действительного переменного наз. аппроксимативно дифференцируемой в точке х 0, если существует такое число А, что При этом величина… … Математическая энциклопедия
Непрерывная дифференцируемость — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
Показатель Гёльдера — (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель Гёльдера является… … Википедия
Показатель Гельдера — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
Показатель Липшица — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
Условие Гельдера — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия