для чего используется формула лоренца
Сила Лоренца и все про нее
Нигде еще школьный курс физики так сильно не перекликается с большой наукой, как в электродинамике. В частности, ее краеугольный камень – воздействие на заряженные частицы со стороны электромагнитного поля, нашло широкое применение в электротехнике.
Формула силы Лоренца
Формула описывает взаимосвязь магнитного поля и основных характеристик движущегося заряда. Но сперва нужно разобраться, что же оно собой представляет.
Определение и формула силы Лоренца
В школе очень часто показывают опыт с магнитом и железными опилками на бумажном листе. Если расположить его под бумагой и слегка потрясти, то опилки выстроятся по линиям, которые принято называть линиями магнитной напряженности. Говоря простыми словами, это силовое поле магнита, которое окружает его подобно кокону. Оно замкнуто само на себя, то есть не имеет ни начала, ни конца. Это векторная величина, которая направлена от южного полюса магнита к северному.
Если бы в него влетела заряженная частица, то поле воздействовало бы на него очень любопытным образом. Она бы не затормозилась и не ускорилась, а всего лишь отклонилась в сторону. Чем она быстрее и чем сильнее поле, тем больше на нее действует эта сила. Ее назвали силой Лоренца в честь ученого-физика, впервые открывшего это свойство магнитного поля.
Вычисляют ее по специальной формуле:
здесь q – величина заряда в Кулонах, v – скорость, с которой движется заряд, в м/с, а B – индукция магнитного поля в единице измерения Тл (Тесла).
Направление силы Лоренца
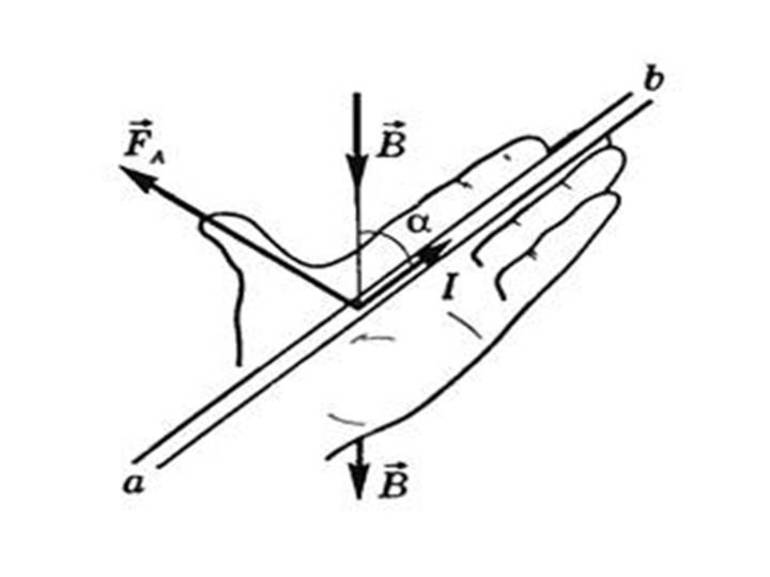
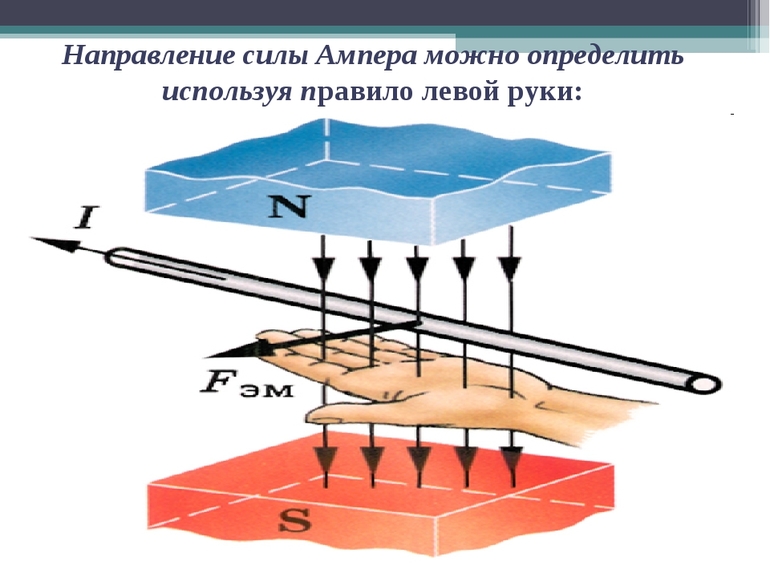
Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.
Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица. В таком случае большой палец покажет, куда она отклонится.
Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица. Все остальные манипуляции остаются прежними.
Следствия свойств силы Лоренца
Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:
sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.
Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.
В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:
Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.
Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:
Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.
Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.
Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.
Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.
Формула силы Лоренца при наличии магнитного и электрического полей
Магнитное поле имеется не только у постоянных магнитов, но и у любого проводника электричества. Только в данном случае помимо магнитной составляющей, в ней присутствует еще и электрическая. Однако даже в этом электромагнитном поле эффект Лоуренса продолжает свое воздействие и определяется по формуле:
где v – скорость электрически заряженной частицы, q – ее заряд, B и E – напряженности магнитного и электрических полей поля.
Единицы измерения силы Лоренца
Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.
Понятие напряженности электрического поля
Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.
То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Напряженность электрического поля
Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:
Единицей измерения является Н/Кл или В/м.
Примеры задачи
Задача 1
На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.
В условиях задачи нет упоминания электрического поля, поэтому силу Лоренца можно найти по следующей формуле:
FЛ=qvBsinα=0,005×200×0,3×sin 450 =0,3×22=0,21 Н
Задача 2
Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.
Чтобы найти скорость заряда, необходимо несколько видоизменить формулу для нахождения силы Лоренца:
v=320,005×2×sin900=320,01×1=32000мс=32 км/с
Задача 3
Электрон движется в однородном магнитном поле под углом 900 ее силовым линиям. Величина, с которой поле воздействует на электрон, равна 5 × 10-13 Н. Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.
В этой задаче сила Лоренца ко всему прочему еще и заставляет двигаться электрон по окружности. Поэтому здесь под ускорением следует понимать центростремительное ускорение:
На данный момент неизвестны ни скорость электрона, ни радиус окружности, по которой он движется.
Электродинамика оперирует такими понятиями, которым трудно подобрать аналогию в обычном мире. Но это совсем не значит, что их невозможно постичь. С помощью различных наглядных экспериментов и природных явлений процесс познания мира электричества может стать по настоящему захватывающим.
Профильное образование: Троицкий аграрный техникум, специальность – электрик 3 разряда (1996 г.).
IV группа допуска по электробезопасности.
Электрик 4 разряда.
Опыт работы – с 1996 года.
Объекты работ: квартиры, дачи, бани, офисы и другие.
Дополнительная информация: Ленинградская область (до 100 км от г. Санкт-Петербурга)
Сила Лоренца: определение, формула, применение на практике
Мари Ампер доказал, что при наличии электрического тока в проводнике, оказавшемся в магнитном поле, он взаимодействует с силами этого поля. Учитывая то, что электрический ток – это не что иное, как упорядоченное движение электронов, можно предположить, что электромагнитные поля подобным образом действуют также на отдельно взятую заряженную частицу. Это действительно так. На точечный заряд действует сила Лоренца, модуль которой можно вычислить по формуле.
Определение и формула
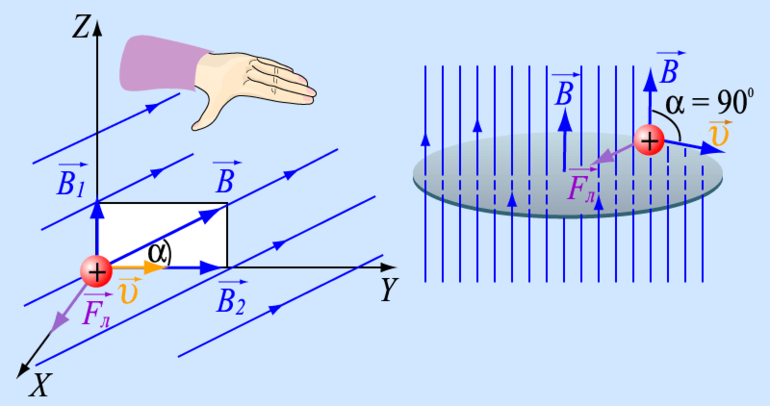
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.

Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.
Учитывая, что
(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:
Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:
Модуль F вычисляется по формуле:
Из формулы следует:
Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).
Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
В чём измеряется?
Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.
Направление силы Лоренца
Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.
Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).

Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.
Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.

Применение на практике
Практическое значение работ Лоренца мы можем наблюдать в электронно-лучевых трубках. Там поток электронов движется в магнитном поле, изменением которого задаётся траектория электронного пучка.
Данный принцип управления траекторией электронного пучка использовался в старых моделях телевизоров Рис. 6). Электроны под воздействием магнитных полей очерчивали линии на люминофоре кинескопа, рисуя изображения на экране.
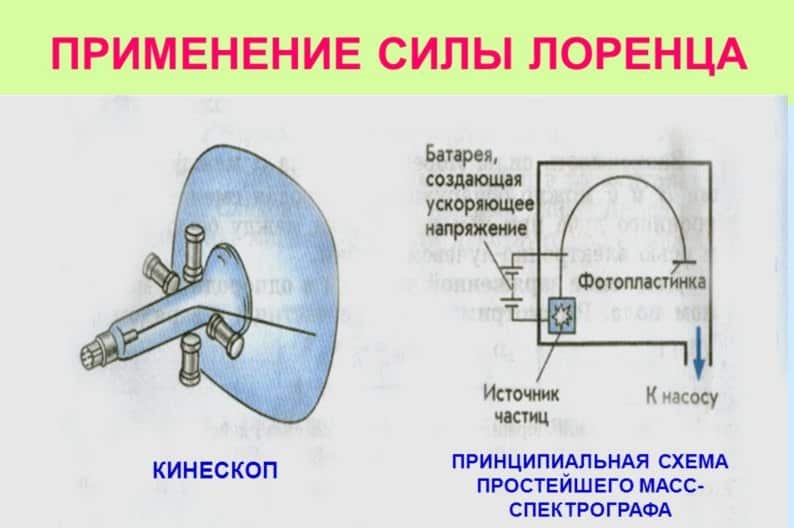
На рисунке справа изображена схема масспектрографа – прибора для разделения заряженных частиц по величине их зарядов.
Ещё один пример – бесконтактный электромагнитный метод определения скорости течения (вязкости) электропроводных жидкостей. Методика может быть применима к расплавленным металлам, например к алюминию. Бесконтактный способ определения вязкости очень полезен при работе с агрессивными жидкими электропроводными веществами (рис. 7).

Работа ускорителей была бы невозможной без участия силы Лоренца. В этих устройствах заряженные частицы удерживаются и разгоняются до околосветовых скоростей благодаря электромагнитам, расположенным вдоль кольцевой трассы.
Мощная электронная лампа – Магнетрон также работает на принципе взаимодействия электронов с магнитными полями, которые направляют высокочастотное излучение в нужном направлении. Магнетрон является основной рабочей деталью микроволновых печей.
На основании действия силы Лоренца создано много других устройств, используемых на практике.
Формулировка и формулы
Частица с зарядом q испытывает силу F, когда движется со скоростью v в электрическом (E) и магнитном (B) полях. Определяется она как F = qE + qv x B и измеряется в единицах СИ — N (ньютон). С точки зрения декартовых компонентов имеется:
E и B — функции положения времени. Следовательно, равенство может быть записано как F (r, ṙ, t, q) = q [E (r, t) + ṙ x B (r, t)], где r — вектор положения заряженной частицы, t — время, а овердот — производная времени.
Ускорение частицы будет происходить в той же линейной ориентации, что и поле E, но станет изгибаться перпендикулярно как вектору мгновенной скорости v, так и полю B. Это говорит о соответствии формулы силы Лоренца и «правила левой руки». Также здесь будет работать и «правило буравчика» (если пальцы расширяются, чтобы указывать в направлении v, а затем скручиваются, показывая в сторону B, тогда большой палец будет смотреть на F).
Комбинация q E называется электрической силой, а q (v + B) — магнитной. В этом контексте её можно называть силой Лапласа. Она не влияет на мощность, потому что всегда перпендикулярна скорости частицы.
Для непрерывного распределения заряда в движении уравнение принимает вид dE = dq (E + v + B). Если обе части равенства будут разделены на объём небольшого фрагмента dV, результат будет выглядеть следующим образом: f = p (E + v x B). Поэтому непрерывным аналогом уравнения является f = pE + J x B, где J — плотность тока.
Суммарная сила — интеграл объёма по распределению заряда: F = ∫∫∫ (p E + J x B) dV. Устраняя p и J, используя уравнения Максвелла и манипулируя с помощью теорем векторного исчисления, эту форму можно использовать для получения тензора напряжения σ. В свою очередь, это можно объединить с вектором Пойнтинга s для получения электромагнитного тензора энергии-импульса T, используемого в общей теории относительности. Если разделить полный заряд и ток на их связанные частицы, то получится плотность силы Лоренца. Она, в свою очередь, может объяснить крутящий момент.
Историческая справка
Ранние попытки количественно описать электромагнитную силу были предприняты только в середине XVIII века. Было высказано предположение, что сила на магнитных полюсах Иоганна Тобиаса Майера и электрически заряженных объектах Генри Кавендиша подчинялась закону обратных квадратов.
Однако в обоих случаях экспериментальное доказательство не было полным и убедительным. Лишь в 1784 году Шарль-Августин де Кулон, используя торсионный баланс, смог окончательно показать, что это правда. После открытия в 1820 году Эрстедом того, что на магнитную стрелку действует ток вольта, Андре-Мари Ампер в том же году смогла разработать формулу угловой зависимости силы между двумя токовыми элементами.
Современная концепция электрический и магнитных полей впервые возникла в теориях Майкла Фарадея, в частности, в его представлении о силовых линиях. Лордом Кельвином и Джеймсом Клерком Максвеллом ему было дано полное математическое пояснение.
Джей Джей Томсон был первым, кто попытался вывести из уравнений поля Максвелла электромагнитные силы на движущийся заряженный объект в терминах его свойств. Однако Томсон был заинтересован выражать эти величины в катодных лучах. Поэтому в 1881 году он публикует статью, где размещает свою формулу F = q/2 v x B. Она оказалась базовой, но из-за некоторых просчётов и неполного описания тока смещения он включил неверный масштабный коэффициент, равный половине.
Оливер Хевисайд изобрёл современную векторную запись и применил её к уравнениям Максвелла. Он также исправил ошибки вывода и пришёл к правильной форме магнитной силы на движущемся заряженном объекте. Наконец, в 1895 году Хендрик Лоренц вывел формулу, которая используется в настоящее время и носит его имя.
Значение и определение
Закон силы Лоренца описывает влияние E и B на точечный заряд, но такое воздействие не показывает всю картину. Заряженные частицы не просто дрейфуют в однородном электромагнитном поле. Возможно, они подвергаются и другим воздействиям, например, гравитации. В реальных материалах выводы физика не подходят для описания коллективного поведения таких частиц, как в принципе и для вычисления, поскольку тела не только реагируют на поля E и B, но и генерируют их.
Сложные уравнения переноса должны решаться для определения временной и пространственной реакции зарядов, например, равенств:
К примеру, для решения вопросов по гидродинамике, электрогидродинамике, сверхпроводимости и эволюции звёзд разработан целый физический аппарат (формулы Грина — Кубо).
Для большей точности следует пояснить, что под силой Лоренца понимается следующее эмпирическое утверждение: F на пробном заряде в данной точке и данном времени является определённой функцией заряда q и скорости V, которая может быть параметризована ровно двумя векторами E и B в форме F = q (E + v x B).
Это справедливо даже для частиц, приближающихся к скорости света. Таким образом, два векторных поля (магнитное и электрическое) определяются во всём пространстве и времени относительно того, какую силу получит испытательный заряд.
Собственно, это только определение в принципе, потому что реальная частица (в отличие от гипотетической) будет генерировать собственные конечные поля E и B, изменяющие электромагнитную силу, которую он испытывает. Кроме того, когда у заряда есть ускорение, как если бы он был вынужден двигаться по искривлённой какими-либо внешними агентами траектории, от него исходит излучение, вызывающие торможение. Эти эффекты происходят как через прямое воздействие, так и косвенное. Помимо прочего, нужно учитывать гравитацию и другие силы.
Усиление и движущая ЭДС
Когда провод, несущий электрический ток, помещается в магнитное поле, каждый из движущихся зарядов, которые составляют ток, испытывает силу Лоренца. Вместе они могут создавать макроскопическую силу Лапласа. Исходя из этого, получается формула F = Iℓ x B, где ℓ — вектор, величина которого и есть длина проволоки. Его направление выровнено с движением обычного тока.
Если проволока не прямая, а изогнутая, расчёт происходит путём применения этого уравнения к каждому бесконечно малому сегменту проводника d ℓ. Затем нужно сложить всё посредством интегрирования. Формально чистая сила равна F = I ∫ dℓ x B. Кроме того, обычно возникает крутящий момент и другие эффекты, если провод не является абсолютно жёстким.
Компонент (qv x B) отвечает за движущую электродвижущей силы (ЭДС). Это явление, лежащее в основе многих электрических генераторов, исключая те, в которых движутся только магниты, а не проводники. В таких случаях ЭДС обусловлена (q E). Такое явление описано уравнением Максвелла — Фарадея.
Обе ЭДС, несмотря на их различное происхождение, описаны законом индукции Фарадея. Теория относительности Эйнштейна была частично мотивирована желанием лучше понять эту связь между двумя эффектами. На самом деле, электрические и магнитные поля являются разными гранями одного и того же электромагнитного поля. Поэтому при переходе от одной инерциальной системы отсчёта в другую (соленоидальное векторное поле) часть E может измениться в целом или частично стать B или наоборот.
Интеграция в другие направления
Применение силы Лоренца и её взаимодействие с другими смежными науками очевидно. Взять хоть аналитическую механику. Например, лоренцевское уравнение можно получить, используя формулы Лагранжа.
Также релятивную форму этого закона можно решить с помощью пространственно-временной алгебры (тип Клиффорда). В общей теории относительности уравнение движения для частицы с массой m и зарядом e, движущейся в пространстве с метрическим тензором g ab и электромагнитным полем F ab, имеет следующее выражение:
m du c / ds — m ½ g ab, c u a u b = eF cb u b ;
Из закона индукции Фарадея (который действителен для движущейся проволоки, например, в двигателе) и уравнений Максвелла можно вывести силу Лоренца. Направление расчётов в обратную сторону также верно. Фарадеевский постулат не зависит от того, является ли проволочная петля жёсткой и неподвижной, находится ли она в движении или в процессе деформации, сохраняется ли магнитное поле постоянным во времени или оно изменяется. Однако есть случаи, когда закон либо неадекватен, либо труден в использовании. Именно здесь необходимо применение основополагающего закона Лоренца.
Широкое применение
Первыми приборами для предполагаемых открытий стали циклотроны. Смысл их работы довольно прост: частицы двигаются полукругом. Каждый раз, когда они проходят определённую область, специальный модуль включает электрическое поле, чтобы ускорить их.
Масс-спектрометры применяются для идентификации атомов и молекул. Они используются в следующих устройствах:
Способность силы Лоренца связывать механическое смещение с электрическим током представляет большой интерес для медицинской акустики. Например, разрабатывался гидрофон для картирования скорости частиц акустического поля. Предполагалось, что он будет построен с использованием тонкого медного провода и внешнего магнитного поля.
Модель была разработана для определения взаимосвязи между акустическим давлением и измеренным электрическим током, который индуцируется, когда провод вибрирует в акустическом поле ультразвукового преобразователя.
Созданный прототип был охарактеризован. Было исследовано его пространственное разрешение, частотная характеристика, чувствительность, надёжность и характеристика направленности. Был также изучен метод визуализации, называемый электрической импедансной томографией. В этом методе биологическая ткань вибрирует ультразвуком в магнитном поле, которое индуцирует электрический ток. Этот метод был применён для визуализации желатинового фантома, образца мышц говядины и термического поражения в образце куриной грудки. Это показало, что метод может быть полезен для обеспечения дополнительного контраста по сравнению с обычной ультразвуковой визуализацией.