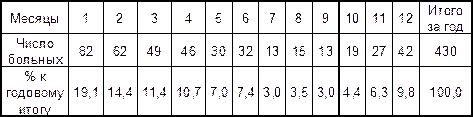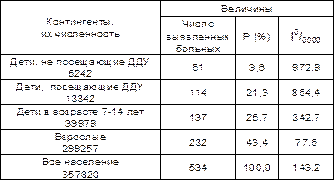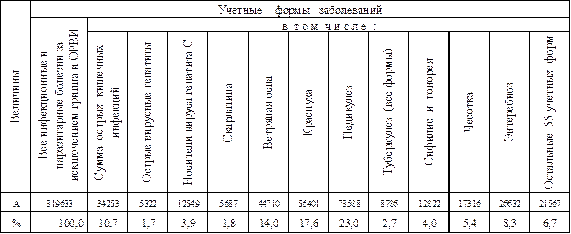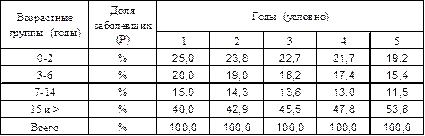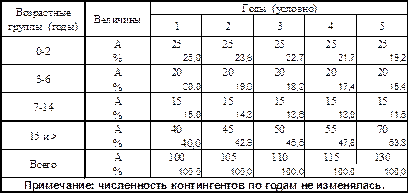для чего используют экстенсивные показатели
Показатели экстенсивные и интенсивные
Показатели экстенсивные (или распределения)
Характеризуют распределение целого на его составные части, т. е. определяют состав этого целого или удельный вес отдельных частей в нем. Экстенсивные показатели выражаются обычно в процентах к итогу.
Например, в стационар Челябинской областной клинической больницы в 1962 г. было госпитализировано 15 962 человека. Из них сельских жителей — 7621, или 47,7%; жителей городов и рабочих поселков — 5313, или 33,3%, и жителей Челябинска — 3028, или 19%.
Такие же процентные отношения вычисляют, если нужно определить соотношение возрастных, половых, социальных групп в составе населения или соотношения между отдельными болезнями в структуре заболеваемости того или иного коллектива и др.
Экстенсивные показатели нельзя применять для установления динамики изучаемого явления во времени или для сравнения степени его распространения в двух или нескольких группах населения.
Показатели интенсивные (распространения частоты)
Характеризуют частоту распространения данного явления. Вычисление этих коэффициентов производится при помощи пропорций, приводящих абсолютные числа к одному основанию, — 1000, 10 000, 100 000 жителей, отношений которого вычисляется коэффициент.
Так, например, интенсивный показатель рождаемости вычисляется отношением числа родившихся на 1000 жителей; так же определяется интенсивный показатель общей смертности.
Интенсивный показатель заболеваемости или смертности определяется по формуле:
Пример
В городе А с числом жителей 65 300 умерло за год 700 человек, в городе Б с числом жителей 93 100 умерло 905 человек. Какова смертность в этих двух городах? Если судить по абсолютным данным, то умерло больше в городе Б. Однако в городе Б и численность населения больше, чем в городе А.
Поэтому для того чтобы решить вопрос в каком городе смертность выше, необходимо в том и другом городе вычислить интенсивный показатель смертности, т. е. показатель смертности на 1000 жителей.
Отсюда видно, что в городе А из каждой 1000 в год умирает 10,7, а в городе Б — 9,7. Эти величины ясно показывают, что смертность в городе А выше, чем в городе Б.
«Справочник помощника санитарного врача
и помощника эпидемиолога»,
под ред. члена-корреспондента АМН СССР
проф. Н.Н.Литвинова
Интенсивные и экстенсивные показатели. Методика вычисления, использование в здравоохранении.
Относительные величины (показатели, коэффициенты) получаются в результате отношения одной абсолютной величины к другой. Наиболее часто используются следующие показатели:
В здравоохранении изучаются заболеваемость, смертность, инвалидность, рождаемость и другие показатели здоровья населения. Средой, в которой происходят процессы, является население в целом или его отдельные группы (возрастные, половые, социальные, профессиональные и др.). В медико-статистических исследованиях явление представляет собой как бы продукт среды. Например, население (среда) и заболевшие (явление); больные (среда) и умершие (явление) и т. д.
Интенсивные показатели могут быть:
Интенсивные показатели применяются в медицине:
— для определения уровня, частоты, распространенности явления
— для сравнения частоты явления в двух различных совокупностях
— для изучения изменений частоты явления в динамике.
Экстенсивные показатели используются для определения структуры явления и сравнительной оценки соотношения составляющих его частей. Экстенсивные показатели всегда взаимосвязаны между собой, т. к. их сумма всегда равна 100 процентам: так, при изучении структуры заболеваемости удельный вес отдельного заболевания может возрасти:
— при истинном росте числа заболеваний
— при одном и том же его уровне, если число других заболеваний снизилось
— при снижении числа данного заболевания, если уменьшение числа других заболеваний происходит более быстрыми темпами.
При анализе экстенсивный показатель следует применять с осторожностью и помнить, что им пользуются только для характеристики состава (структуры) явления в данный момент времени и в данном месте.
Примеры использования в работе врача: лейкоцитарная формула; структура населения по полу, возрасту, социальному положению; структура заболеваний по нозологии; структура причин смерти.
Примеры использования в работе врача: показатели обеспеченности населения врачами, больничными койками; показатели, отражающие число лабораторных исследований на 1 врача и т.д.
Показатели наглядности указывают, на сколько процентов или во сколько раз произошло увеличение или уменьшение сравниваемых величин. Показатели наглядности используются чаше всего для сравнения данных в динамике, чтобы представить закономерности изучаемого явления в более наглядной форме.
При пользовании относительными величинами могут быть допущены некоторые ошибки:
1. иногда судят об изменении частоты явления на основе экстенсивных показателей, которые характеризуют структуру явления, а не его интенсивность.
2. нельзя складывать и вычитать статистические показатели, которые рассчитаны из совокупностей, имеющих разную численность, ибо это приводит к грубым искажениям показателя.
3. при расчете специальных показателей следует правильно выбирать знаменатель для расчета показателя: например, показатель послеоперационной летальности необходимо рассчитывать по отношению к оперированным, а не всем больным.
4. при анализе показателей следует учитывать фактор времени: нельзя сравнивать между собой показатели, вычисленные за различные периоды времени (показатель заболеваемости за год и за полугодие), что может привести к ошибочным суждениям.
5. нельзя сравнивать между собой общие интенсивные показатели, вычисленные из неоднородных по составу совокупностей, поскольку неоднородность состава среды может влиять на величину интенсивного показателя.
111. Показатели соотношения и наглядности. Методика вычисления, использование в здравоохранении – см. вопрос 110.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Экстенсивные показатели



Экстенсивные показатели, или показатели структуры (т.е. внутреннего строения, устройства) изучаемого явления оценивают величину какой-либо структурной части ко всему явлению. Измеренные части явления называют долямиилиудельными весами, оценивающими вклад каждой части в общее явление.
Размерность экстенсивных показателей (т.е. долей, удельных весов, вкладов) принципиально может быть любой, но чаще всего ее выражают в процентах, реже – в долях единицы, принимая целое, соответственно за 100 или за 1.
При изучении структуры заболеваемости общая формула расчета:
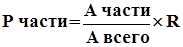
Р части – экстенсивный показатель заболеваемости, оценивающий удельный вес какой-либо структурной части заболеваемости (заболевших) в известном суммарном числе заболевших;
А части – число случаев болезни, относящееся к какой-либо структурной части заболевших (группе больных);
А всего – (основание показателя) – число случаев болезни, отражающее всю, существующую в пределах данной структуры, заболеваемость, т.е. суммарное число больных во всех группах составляющих данную структуру;
R – размерность показателя – проценты (%).
При изучении структуры заболеваемости используются различные группировочные признаки, позволяющие делить всех больных на группы (структурные части) и создавать, таким образом, различные структурные распределения определенного, часто одного и того же, суммарного числа больных. Ниже приведены некоторые примеры различных структурных распределений.
Так, использование в качестве группировочного признака диагноза заболевания позволяет изучить структуру заболеваемости по нозологическим формам болезней.
В 2002 г. в Москве было выявлено 2712880 больных, относящихся к 75 нозологическим формам инфекционных и паразитарных болезней. В том числе, 2300430 больных острыми респираторными болезнями (ОРВИ), 92817 больных гриппом, 34253 больных различными острыми кишечными инфекциями (ОКИ), 56401 больных краснухой и так далее.
Исходя из этих данных доля (удельный вес, вклад) заболевших каждой из этих болезней в общей сумме всех больных всеми инфекционными и паразитарными болезнями составил:
Р больных ОРВИ= (2300430/2712880)´100 = 84,8%
Р больных гриппом = (92817/2712880)´100 = 3,4%
Р больных ОКИ = (34253/2712880)´100 = 1,3%
Р больных краснухой = (56401/2712880)´100 = 2,1%
Не менее важным является анализ структурных распределений составленных с учетом времени возникновения случаев болезни.
Например, данные табл..2 позволяют оценить вклад заболевших в каждом месяце в общую сумму заболевших за год.
.
Табл. 2 Помесячное распределение больных скарлатиной среди всего населения г. В. в 2000 году
Использование для группировки различных индивидуальных признаков, позволяет создавать и изучать разнообразные структурные распределения больных, например, по полу, возрасту, профессиям, особенностям клинического течения болезни и т.д.
В 2000 году в Москве было выявлено 272954 больных 73 инфекционными и паразитарными болезнями. Среди них было 696835 больных детей в возрасте до 7 лет, 649395 больных детей в возрасте 7 – 14 лет и 1381724 больных взрослых. Соответственно удельный вес каждой указанной возрастной группы составил:
Р больных детей до 7 лет=(696865/272954)´100 = 25,6%
Р больных детей 7 –14 лет = (649395/272954)´100 =23,8%
Р больных взрослых = (1381724/272954)´100 = 50,8%
Экстенсивный показатель, оценивающий долю какой-либо части заболеваемости, должен иметь все те же названия, что и интенсивный показатель, т.е. название болезни, время, место возникновения случая болезни, обозначение индивидуальных признаков больных. Кроме того, обязательнодолжна быть обозначена (названа) общая сумма заболевших, принимаемая за А всего,т.е. сумма заболевших составляющая данное структурное распределение.
Абсолютно бесполезной является следующая информация – «в Москве в 2002 г удельный вес заболевших скарлатиной детей до 14 лет составил 5,2%».
Бесполезность этой информации связана с отсутствием обозначения той суммы больных, для которой определялась доля детей больных скарлатиной. Доля таких больных (а всего было выявлено 5687 детей до 14 больных скарлатиной) будет существенно различаться в зависимости от того, какие цифры принимаются за суммарное количество больных. Например, возможны следующие варианты:
· доля больных скарлатиной детей рассчитанная исходя из суммарного числа больных детей до 14 лет в Москве в 2002 г. независимо от наименования инфекционной болезни составит – Р=(5687/1341569)´100=0,42%;
· доля больных скарлатиной детей, рассчитанная исходя из общего числа всех (независимо от возраста) больных инфекционными и паразитарными болезнями в Москве в 2002 г. составит – Р=(5687/2712880)´100=0,21%;
· доля больных скарлатиной детей, рассчитанная исходя из суммарного числа больных 6 детскими инфекциями (коклюшем, скарлатиной, натуральной оспой, корью, краснухой и эпидемическим паротитом) составит – Р=(5687/108638)´100=5,2%
Таким образом, информация, указанная в начале примера, относится только к последнему структурному варианту оценки удельного веса детей до 14 лет заболевших скарлатиной в Москве в 2002 г.
В отличие от интенсивных показателей, экстенсивные показатели заболеваемости можно объединить, но при условии, если они относятся к одному структурному распределению.
По данным предыдущего примера доли больных всеми инфекционными и паразитарными болезнями в Москве в 2000г. составили для детей:
Величина экстенсивных показателей при сравнимом качестве выявления, диагностики и учета больных, зависит от влияния большего количества факторов, чем величина интенсивных показателей.
Значение отдельного интенсивного показателя, отражающего частоту заболеваний в отдельной группе населения, определяется только:
· риском заболеть (заразиться и заболеть) представителей исключительно данной группы;
· численностью данной группы населения.
Следовательно, изменение интенсивного показателя одной группы населения никак не сказывается на величине интенсивных показателей в других группах.
Значение отдельного экстенсивного показателя, отражающего долю заболевших отдельной группы населения в общей сумме больных, принятых за 100%, определяется:
· риском заболеть (заразиться и заболеть) характерным не только для данной группы, но и других групп населения;
· численностью каждой группы населения, входящей в данное распределение заболевших.
Именно поэтому величина экстенсивных показателей и их изменение может зависеть с равной вероятностью, как от факторов присущих отдельной группе населения, так и факторов влияющих на число заболевших в других группах.
При трактовке результатов изучения структуры заболеваемости, к сожалению, допускаются типичные и серьезные ошибки.
Во избежание такой ошибки необходимо помнить и понимать формулы расчетов интенсивных и экстенсивных показателей заболеваемости. Числители этих показателей одинаковы – абсолютное число больных в определенных группах населения. Знаменатели этих показателей разные. У интенсивного показателя знаменатель – численность определенной группы населения, у экстенсивного показателя знаменатель – суммарное число больных в изучаемых группах. Вследствие этого величины интенсивного и экстенсивного показателя заболеваемости какой-либо группы населения статистически абсолютно независимы друг от друга. Так, например, при одной и той же частоте заболеваний в разных группах населения, доли заболевших, относящихся к этим группам, могут существенно различаться, причем тем больше, чем больше различается численность отдельных групп населения. Сравнительно незначительный риск возникновения заболевания за счет большой численности группы может обеспечить высокий вклад больных этой группы в общую заболеваемость населения. И наоборот, высокий риск возникновения болезни в группе населения небольшой численности может проявиться незначительной долей заболевших.
Табл. 3. Заболеваемость дизентерией различных групп населения г. В. в 2000 г.
Как следует из данных табл. 3 – основной вклад (43.4%) в заболеваемость дизентерией в 2000 г. в г. В. внесли взрослые. Удельный вес детей, не посещающих ДДУ заболевших дизентерией, был в 4,5 раза меньшим и составил 9,6%. Однако, на основании только этих данных нельзя сделать вывод о том, что рискзаболеть дизентерией взрослых – наибольший, а аналогичный риск детей, не посещающих ДДУ – наименьший.
Различная доля заболевших в разных группах населения может быть связана не столько с разным риском заболеть дизентерией, сколько с различной численностью сравниваемых групп.
Именно поэтому соотношение интенсивных показателей оказалось прямо противоположным – риск заболеть дизентерией детей, не посещающих ДДУ был в 12 раз выше, чем аналогичный риск взрослых. Однако, сравнительно небольшой риск взрослых, за счет значительно большей их численности обеспечил почти половину всех больных дизентерией.
Таким образом, по величине экстенсивных показателей заболеваемости не следует делать выводы о частоте и риске заболеваемости в разных группах населения.
Исключением из этого правила являются такие распределения экстенсивных показателей, в которых оцениваются доли заболевших, относящихся к одной и той же группе населения
Поскольку все величины таблицы 4 относятся к одной и той же численности населения, т.е. численности населения Москвы в 2002 г., соотношение экстенсивных показателей соответствует соотношению интенсивных величин заболеваемости. Следовательно, таким же является и соотношение риска заболеть различными болезнями населения Москвы в 2002 г. Так, на основании представленных данных можно утверждать, что риск возникновения педикулеза был почти в 13 раз выше, чем риск заболеть скарлатиной (23,0/1,8=12,8).
Другая типичная ошибка связана с трактовкойдинамики экстенсивных показателей (табл. 5). Например, уменьшение удельного веса заболевших какой-либо группы пытаются объяснить влиянием факторов, определяющих заболеваемость только в той же группе, в частности, эффективностью противоэпидемических мероприятий, проводимых в отношении этой группы населения.
При изучении динамики экстенсивных показателей следует учитывать то, что уменьшение (увеличение) числа больных даже в одной группе и, следовательно, изменение общего числа больных, приведет к перераспределению долей во всех группах. Таким образом, наблюдаемое уменьшение (увеличение) вклада какой-либо группы в общую заболеваемость может быть связано с изменением численности больных как в этой, так и других группах населения.
Табл. 5.Заболеваемость болезнью К различных возрастных групп населения г. Н в течение 5 условных лет (Р – доля заболевших каждой группы в общей сумме заболевших за год).
Как следует из представленных данных, во всех группах, за исключением взрослых, отмечается явная тенденция снижения экстенсивных показателей заболеваемости. Однако было бы грубой ошибкой только на основании этого факта делать вывод о снижении риска заболеть болезнью К большинства групп населения г. Н.
Выявленная динамика экстенсивных показателей может быть следствием различных ситуаций, часть которых иллюстрируется табл. 6.
Табл. 6. Данные табл. 5 дополнены абсолютными числами заболевших (А).
Как следует из представленных данных, число заболевших в группах детей абсолютно не изменилось, тогда, как среди взрослых число заболевших постепенно увеличивалось. Учитывая, что численность возрастных групп не изменялась(см. примечание), без расчета интенсивных показателей можно сделать вывод о том, что риск заболеть болезнью К постепенно увеличился только для взрослого населения г.Н. В результате каждый год увеличивалось число заболевших среди взрослых и, естественно на ту же величину возрастало общее число заболевших среди всего населения. По этой причине, несмотря на то, что абсолютное число больных в остальных группах не изменялась, удельного веса заболевших детей постоянно снижался. Таким образом такое снижение произошло не за счет уменьшения риска заболеть в этих группах, а из-за увеличения риска заболеть взрослых и следовательно из-за увеличения общего число заболеваний. Поскольку общая численность всего населения не изменялась частота заболеваний болезнью К всего населения также увеличилась.
Заканчивая обсуждение интенсивных и экстенсивных показателей заболеваемости приведем сводную сравнительную характеристику свойств и возможностей этих показателей.
Для чего используют экстенсивные показатели
Абсолютные величины несут важную информацию о размере того или иного явления и могут быть использованы в анализе, в том числе в сравнительном. Однако они часто не отвечают на все поставленные вопросы, так, например, врачу интересны сведения о здоровье обслуживаемого населения (показатели заболеваемости и др.), а у него есть информация только в абсолютных числах, которые термин «заболеваемость» не характеризуют.
Для более углубленного анализа общественного здоровья и деятельности учреждений здравоохранения, а также деятельности медицинского работника используются обобщающие показатели, называемые относительными величинами. Они применяются для изучения совокупности, которая характеризуется, главным образом, альтернативным распределением качественных признаков.
Различают четыре вида относительных величин: экстенсивные, интенсивные, соотношения и наглядности.
Это показатель удельного веса, доли части в целой совокупности, показатель распределения совокупности на составляющие ее части, т.е. показатель структуры.
Для его расчета необходимо иметь данные о численности всей совокупности и составляющих ее частях (или отдельной части этой совокупности). Рассчитывается обычно в процентах, где совокупность в целом принимается за 100%, а отдельные части — за «X».
Способ получения экстенсивной величины выглядит следующим образом:
Таким образом, для получения экстенсивного показателя нужна совокупность и ее составные части или отдельная часть. Экстенсивный показатель отвечает на вопрос, сколько процентов приходится на каждую конкретную часть совокупности.
Это показатель статики, т.е. с его помощью можно анализировать конкретную совокупность в конкретный момент. По экстенсивным показателям нельзя сравнивать различные совокупности — это приводит к неправильным, ошибочным выводам (см. Ошибки использования относительных величин).
Пример расчета экстенсивного показателя
В районе А в текущем году было зарегистрировано 500 случаев инфекционных заболеваний, из них: эпидемического паротита — 60 случаев; кори — 100 случаев; прочих инфекционных заболеваний — 340 случаев.
Задание: определить структуру инфекционных заболеваний, проанализировать и представить графически.
Решение: Вся совокупность — 500 случаев инфекционных заболеваний принимается за 100 %, составные части определяются как искомые. Удельный вес случаев эпидемического паротита составит: 60 x 100% / 500 = 12%.
Аналогично рассчитывается удельный вес других заболеваний.
Вывод. В структуре инфекционных заболеваний доля эпидемического паротита составила 12%, кори — 20%, прочих инфекционных заболеваний — 68%.
Способы графического изображения экстенсивного показателя
Поскольку экстенсивный показатель — показатель статики, то графически он изображается только в виде внутристолбиковой или секторной (круговой) диаграммы, которые являются разновидностями плоскостных диаграмм, которые представляют цифровые данные в виде геометрических фигур в двух измерениях.
Правила построения этих диаграмм можно представить, использовав при этом полученные данные удельного веса заболеваний в приведенном выше примере.
Пример построения внутристолбиковой диаграммы (диаграмма 1, Б):
Вышеизложенные данные можно представить также в виде внутристолбиковой диаграммы, принцип построения которой заключается в следующем: высота прямоугольника (масштаб выбирается произвольно) составляет всю совокупность и принимается за 100%. Удельный вес отдельных частей следует показать внутри прямоугольника, расположив части снизу вверх в порядке убывания процентов, при этом группа «прочие заболевания», так же как и в секторной диаграмме, откладывается последней. Все части выделяются различной штриховкой или расцветкой.
Каждый график должен иметь номер, четкое название, раскрывающее его сущность, масштаб с указанием единиц измерения и экспликацию, отражающую смысл принятых условных изображений.
Показатель частоты, уровня, распространенности процессов, явлений, совершающихся в определенной среде. Он показывает, как часто встречается изучаемое явление в среде, которая его продуцирует (заболеваемость, смертность, рождаемость и т.д.).
Интенсивные показатели используются как для сравнения, сопоставления динамики частоты изучаемого явления во времени, так и для сравнения, сопоставления частоты этого же явления в один и тот же промежуток времени, но в различных учреждениях, на различных территориях и т.д.
Для расчета интенсивного показателя необходимо иметь данные об абсолютном размере явления и среды, его продуцирующей. Абсолютное число, характеризующее размер явления, делится на абсолютное число, показывающее размер среды, внутри которой произошло данное явление, и умножается на 100, 1000 и т.д.
Таким образом, способ получения интенсивного показателя выглядит следующим образом:
Таким образом, для расчета интенсивного показателя всегда нужны две статистические совокупности (совокупность № 1 — явление, совокупность № 2 — среда), причем изменение размера среды может повлечь за собой изменение размера явления.
Множитель (основание) зависит от распространенности явления в среде — чем реже оно встречается, тем больше множитель. В практике для вычисления некоторых интенсивных показателей множители (основания) являются общепринятыми (так, например, показатели заболеваемости с временной утратой трудоспособности рассчитываются на 100 работающих или учащихся, показатели летальности, частоты осложнений и рецидивов заболеваний — на 100 больных, демографические показатели и многие показатели заболеваемости — на 1000, 100 000 населения).
Пример расчета интенсивного показателя.
В городе проживает 120 000 человек (среда). В предыдущем году родилось 108 детей (явление).
Определить показатель рождаемости (рассчитывается на 1000 населения).
Таким образом, рождаемость в городе составила 9%.
Способы графического изображения интенсивного показателя
Пример. Представить информацию о распространенности наркомании (табл. 1) в виде линейной диаграммы.
Таблица 1. Распространенность наркомании в РФ в динамике с 1980 по 2006 г. (на 100 000 населения)
| Наименование показателя | Годы | ||||
| 1980 | 1990 | 2000 | 2003 | 2006 | |
| Число наркоманов в перцентилях | 10,1 | 16,9 | 20,4 | 32,3 | 109,6 |
В нашем примере необходимо нанести на координатное поле 2 ряда цифр — частота наркомании и годы. В соответствии с установленными требованиями к построению графиков необходимо соблюдать соотношение между масштабом по оси абсцисс и ординат как равное 3:4 или 5:8. В данном случае график будет более наглядным.
В примере на оси абсцисс (горизонтальная линия) в соответствии с выбранным исследователем масштабом отмечаются анализируемые годы, на оси ординат (вертикальная линия) в соответствии с вышеуказанным правилом — частота наркомании. В соответствии с построенными осями на координатное поле наносятся величины частоты наркомании соответствующего года. При последовательном соединении точек на графике получится непрерывная линия, наглядно представляющая динамику распространенности наркомании.
Вывод. Анализ диаграммы позволяет наглядно представить постоянный рост частоты наркомании в РФ за 1980-2006 гг.
Пример. Представить информацию (табл. 2) о сезонных изменениях заболеваемости дизентерией в виде радиальной диаграммы.
Таблица 2. Сезонные изменения числа заболеваний дизентерией за изучаемый год в городе Н.
| Наименование | Месяцы года | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Число заболеваний дизентерией | 2 | 7 | 5 | 9 | 15 | 26 | 15 | 35 | 22 | 14 | 3 | 1 |
Длина отрезка соответствующего месяца может выходить за пределы окружности или находиться внутри окружности в зависимости от величины соответствующего месячного показателя числа случаев заболеваний дизентерией (в нашем примере число случаев дизентерии за IV месяц — 15, VII — 15, X — 22 выше среднемесячного показателя, а в остальные месяцы — меньше). Конечные точки отрезков соединяются линиями.
Вывод. Анализ диаграммы позволяет увидеть значительные увеличения числа случаев заболевания дизентерией в летне-осенний период (с апреля по октябрь).
Интенсивные показатели графически изображаются также в виде плоскостных диаграмм. К ним относятся — столбиковые и ленточные диаграммы.
В виде столбиков целесообразно изображать интенсивные показатели для одного периода, но для разных заболеваний, территорий, коллективов или, наоборот, в разные периоды времени, но для одного заболевания, территории, коллектива.
При построении столбиковых диаграмм основание располагают на оси абсцисс. На оси ординат отмечают величину изучаемого признака в принятом масштабе. Ширина столбиков должна быть одинаковой. Столбики могут располагаться как на расстоянии друг от друга, так и рядом друг с другом.
Пример построения столбиковой диаграммы. Представить информацию (табл. 3) об инфекционной заболеваемости в виде столбиковой диаграммы.
| Таблица 3. Заболеваемость населения РФ скарлатиной и коклюшем в предыдущем и изучаемом годах (на 100 000 населения) | ||
| Вид заболевания | Годы | |
| предыдущий год | изучаемый год | |
| Скарлатина | 83,6 | 44,4 |
| Коклюш | 16,9 | 19,1 |
Для построения диаграммы необходимо на оси ординат поместить шкалу с нанесенными на ней делениями в соответствии с принятым масштабом, отражающими показатели заболеваемости.
Вывод. Диаграмма наглядно иллюстрирует значительное снижение заболеваемости населения РФ в изучаемом году скарлатиной и коклюшем.
Пример построения ленточной диаграммы. Представить информацию о заболеваемости с ВУТ в виде ленточной диаграммы (табл. 4).
| Таблица 4. Число случаев заболеваний с временной утратой трудоспособности (ЗВУТ) на 100 работающих различного возраста на предприятии Н. в изучаемом году | ||||||||
| Возраст | До 19 лет | 20-35 | 36-49 | 50 и старше | ||||
| Пол | М | Ж | М | Ж | М | Ж | М | Ж |
| Случаи ЗВУТ | 83,0 | 63,9 | 106,2 | 79,2 | 117,7 | 108,9 | 100,0 | 92,0 |
Для графического изображения в виде ленточной диаграммы изображения случаев заболеваемости с временной утратой трудоспособности выбираем основной признак, по которому будем строить диаграмму. В данном случае был выбран возраст.
На оси абсцисс в центре отмечаем отрезок длиной 1,5-2 см. Из крайних точек этого отрезка справа и слева восстанавливаем перпендикуляры, на которых откладываем одинаковые отрезки: они являются основаниями лент или горизонтальных «столбиков». Расстояние между лентами и их ширина должны быть одинаковыми, а число «лент» как справа (для женщин), так и слева (для мужчин) должно соответствовать количеству градаций основного признака. В данном примере их четыре — по числу возрастных группировок: до 19 лет, 20-35 лет, 36-49 лет, 50 лет и старше. Эти цифры вписываем между основаниями намеченных горизонтальных столбиков. Длина «лент» должна соответствовать размеру изображаемого явления в соответствии с выбранным масштабом. В нашем примере масштаб: 10 случаев утраты трудоспособности — 1 см.
Вывод. На диаграмме наглядно представлено наибольшее число случаев с временной утратой трудоспособности как у мужчин, так и у женщин в возрасте 36-49 лет, а наименьшее — у женщин в возрасте до 19 лет. Однако у мужчин практически во всех возрастных группировках число случаев утраты трудоспособности выше, чем у женщин, кроме возраста 50 лет и старше.
Характеризует соотношение между двумя не связанными между собой совокупностями (обеспеченность населения койками, врачами, дошкольными учреждениями, соотношение родов и абортов, соотношение врачей и медицинских сестер и др.).
Для получения этого показателя нужны две совокупности (совокупность № 1 и № 2). Абсолютная величина, характеризующая одну совокупность (совокупность № 1) делится на абсолютную величину, характеризующую другую, с ней не связанную совокупность (совокупность № 2) и умножается на множитель* (100, 1000, 10 000 и т.д.):
Показатель соотношения = совокупность №1 / совокупность №2 х 10 000
* При расчете показателя соотношения можно не учитывать множитель, например, определяя соотношение родов и абортов
Пример: В городе 120 000 населения, общее число терапевтических коек — 300. Число коек — совокупность № 1, численность населения — совокупность № 2. Требуется рассчитать обеспеченность населения терапевтическими койками.
Показатель соотношения = 300 / 120 000 х 10 000
Вывод. На 10 000 населения в городе приходится 25 терапевтических коек, или обеспеченность населения города терапевтическими койками равна 25 коек на 10 000 населения.
Графически показатель соотношения может быть представлен такими же диаграммами, как и интенсивный показатель.
Применяется для анализа однородных чисел и используется когда необходимо «уйти» от показа истинных величин (абсолютных чисел, относительных и средних величин). Как правило, эти величины представлены в динамике.
Для вычисления показателей наглядности одна из сравниваемых величин принимается за 100% (обычно, это исходная величина), а остальные рассчитываются в процентном отношении к ней.
Особенно их целесообразно использовать, когда исследователь проводит сравнительный анализ одних и тех же показателей, но в разное время или на разных территориях.
Пример 1. Рассчитать показатели наглядности для уровней госпитализации в больничные учреждения городов Н. и К. в динамике за 5 лет наблюдения и представить графически.
Таблица 5. Уровень госпитализации в больничные учреждения в городах Н. и К. за 5 лет (на 100 человек населения)
| Показатели | Годы | |||||||||||
| 1 | 2 | 3 | 4 | 5 | ||||||||
| Уровень госпитализации в городе Н. | 24,4 | 22,8 | 21,2 | 20,5 | 20,7 | |||||||
| Показатель наглядности, % | 100 | 93,44 | 86,9 | 84,0 | 84,7 | |||||||
| Уровень госпитализации в городе К. | 30,0 | 32,0 | 34,0 | 38,0 | 40,0 | |||||||
| Показатель наглядности, % | 100 | 106,75 | 113,3 | 126,7 | 133,3 | |||||||
Решение.
Снижение количества больных, поступивших в стационары будет нагляднее, если приравнять показатель исходного уровня госпитализации в городе Н. (1 год — 24,4) за 100%, а остальные показатели пересчитать в процентах по отношению к нему.
Аналогично рассчитываются показатели наглядности, характеризующие уровень госпитализации в больничные учреждения города К.
Вывод. В динамике за 5 лет наблюдения уровень госпитализации больных в городе Н. снижается, а в городе К. повышается.
Графически полученные данные можно представить на оси координат или в виде столбиковой диаграммы.
Пример 2. Сравнить число коек в больницах А, Б и В и представить графически (табл. 6).
| Таблица 6. Число коек в больницах А, Б и В города Н. | ||
| Больница | Число коек | Показатели наглядности, % |
| А | 300 | 100 |
| Б | 450 | 150 |
| В | 600 | 200 |
Принимаем число коек в больнице А (300 коек) за 100%, тогда для » больницы Б показатель наглядности составит:
Аналогично рассчитывается показатель наглядности для больницы В. Он составил 200%.
Вывод. Число коек в больнице Б на 50 %, а в больнице В на 100% больше, чем в больнице А.
Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов