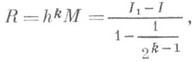для чего используют правило рунге

Правило Рунге

Правило Рунге — правило оценки погрешности численных методов.

Основная идея (для методов Рунге-Кутты решения ОДУ) состоит в вычислении приближения выбранным методом с шагом h, а затем с шагом h/2, и дальнейшем рассмотрении разностей погрешностей для этих двух вычислений.

Применение правила Рунге

Оценка точности вычисления определённого интеграла

Интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) при числе шагов, равном n, а затем при числе шагов, равном 2n. Погрешность вычисления значения интеграла при числе шагов, равном 2n, определяется по формуле Рунге:
, для формул прямоугольников и трапеций , а для формулы Симпсона .
Таким образом, интеграл вычисляется для последовательных значений числа шагов , где n₀ — начальное число шагов. Процесс вычислений заканчивается, когда для очередного значения N будет выполнено условие , где ε — заданная точность.

Полезное

Смотреть что такое «Правило Рунге» в других словарях:

РУНГЕ ПРАВИЛО — один пз методов оценки погрешности формул численного интегрирования. Пусть остаточный член формулы численного интегрирования, где h длина отрезка интегрирования или какой то его части, k фиксированное число и М произведение постоянной на… … Математическая энциклопедия

Квадратурные формулы — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Численное интегрирование — (историческое название: (численная) квадратура) вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла. Численное… … Википедия

Источник

Правило Рунге практической оценки погрешности

5.5 Правило Рунге практической оценки погрешности

Оценки погрешности по формулам (5.4), (5.8) и (5.12) являются априорными. Они зависят от длины элементарного отрезка h, и при достаточно малом h справедливо приближенное равенство:

где I h приближенное значение интеграла, вычисленное по одной из формул (5.3), (5.5), (5.9), C ¹ 0 и k > 0 – величины, не зависящие от h.

Если уменьшить шаг h в два раза, то, в соответствии с (5.15) получим:

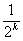
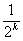
I – I h/ 2 » Ch k » ( I – I h ). (5.16)

Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки.

Вычтем из равенства (5.15) равенство (5.16):

I h/ 2 – I h » 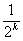Ch k (2 k – 1). (5.17)

Учитывая приближенное равенство (5.16), получим следующее приближенное равенство:

I – I h/ 2 » 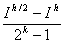. (5.18)

Для формул прямоугольников и трапеций k = 2, а для формулы Симпсона k = 4. Поэтому для этих формул приближенное равенство (5.18) принимает вид:

I – I_пр» 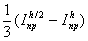, (5.19)

I – I_тр» 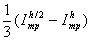, (5.20)

I – I_С » 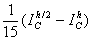. (5.21)

Используя правило Рунге, можно построить процедуру приближенного вычисления интеграла с заданной точностью e. Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значения в два раза, каждый раз вычисляя приближенное значение I 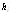. Вычисления прекращаются тогда, когда результаты двух последующих вычислений будут различаться меньше, чем на e.

Источник

Метод дробления шага. Правило Рунге. Формулы (4.12) и (4.14) для практики неудобны, т.к

Формулы (4.12) и (4.14) для практики неудобны, т.к. значения f ( k ) (x) обычно неизвестны. Правило Рунге позволяет найти достаточно точные оценки погрешности, используя значения I*, вычисленные при различных h.

Согласно полученным оценкам, погрешность составных формул численного интегрирования имеет вид

где I и I h – точное значение интеграла и значение, найденное по составной формуле при шаге h, соответственно; С – некоторая константа; m – порядок точности численного метода (согласно формулам (4.12) и (4.14), m = 2 для формулы трапеции и m = 4 для формулы Симпсона).

Уменьшим шаг вдвое. Будем иметь:

Вычтем (4.16) из (4.15). Получим: I h /2 – I h » 2 – m ×C×h m (2 m – 1) = (I – I h /2 )(2 m – 1).

. (4.17)

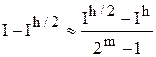
Формула (4.17) – оценка погрешности вычисления I h /2 по правилу Рунге. Если значение правой части приближенного равенства (4.17) окажется меньше предельно допустимой погрешности e, то можно считать I h /2 ответом задачи. В противном случае – требуемая точность не достигнута и необходимо использовать более мелкий шаг, т.е. продолжить процесс дробления шага.

Замечание. При приближённом вычислении интегралов, абсолютная величина | I | которых мала, использование значения абсолютной погрешности D для контроля точности необоснованно, более приемлема относительная погрешность d. Поэтому при использовании правила Рунге рекомендуется следующий критерий останова процесса дробления шага:

если | I h /2 | ³ 1, то заканчивать при ,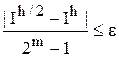

если | I h /2 |

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

РУНГЕ ПРАВИЛО

Согласно Р. п. вычисляется тот же самый интеграл по той же формуле численного интегрирования, но вместо hберется величина h/2. При этом, чтобы получить значение интеграла по всему отрезку, формула интегрирования применяется дважды. Если производная, входящая в М, меняется не сильно на рассматриваемом промежутке, то

Смотреть что такое «РУНГЕ ПРАВИЛО» в других словарях:

Правило Рунге — правило оценки погрешности численных методов. Основная идея (для методов Рунге Кутты решения ОДУ) состоит в вычислении приближения выбранным методом с шагом h, а затем с шагом h/2, и дальнейшем рассмотрении разностей погрешностей для этих двух… … Википедия

КОШИ ЗАДАЧА — численные методы решения для обыкновенного дифференциального уравнения. Задачей Коши наз. задача определения функции или нескольких функций, удовлетворяющих одному или, соответственно, системе дифференциальных уравнений и принимающих заданные… … Математическая энциклопедия

Квадратурные формулы — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Источник

Метод Рунге

Ме́тоды Ру́нге — Ку́тты (распространено неправильное название Ме́тоды Ру́нге — Ку́тта или даже Ме́тоды Ру́нге — Кутта́) — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Содержание

Классический метод Рунге — Кутты четвёртого порядка

Метод Рунге — Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге — Кутты.

Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

Вычисление нового значения проходит в четыре стадии:

где — величина шага сетки по .

Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок (ошибка на каждом шаге порядка ).

Прямые методы Рунге — Кутты

Семейство прямых методов Рунге — Кутты является обобщением метода Рунге — Кутты четвёртого порядка. Оно задаётся формулами

где — величина шага сетки по и вычисление нового значения проходит в этапов:

Конкретный метод определяется числом и коэффициентами и . Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Бутчера)

Для коэффициентов метода Рунге — Кутты должны быть выполнены условия для . Если требуется, чтобы метод имел порядок , то следует также обеспечить условие

где — приближение, полученное по методу Рунге — Кутты. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений относительно коэффициентов метода.

Произношение

Решение систем ОДУ

Метод Ру́нге — Ку́тты непосредственно обобщается на случай систем обыкновенных дифференциальных уравнений путём записи системы и метода в векторной форме.

Пример решения на алгоритмических языках программирования

производя замену и перенося в правую часть, получаем систему:

В программе на С# используется абстрактный класс RungeKutta, в котором следует переопределить абстрактный метод F, задающий правые части уравнений.

Пример решения в среде MATLAB

Имя файла и имя функции должно совпадать, но оно может быть любым неиспользуемым ранее.

Затем необходимо создать главный файл c именем, например, main.m, который будет выполнять основные вычисления. Этот главный файл будет содержать следующий текст:

См. также

Ссылки

Полезное

Смотреть что такое «Метод Рунге» в других словарях:

Метод Рунге — Кутта — Методы Рунге Кутта (Методы Рунге Кутты) важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года… … Википедия

Метод Рунге — Кутты — Методы Рунге Кутта важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К.… … Википедия

Метод Рунге-Кутта — Методы Рунге Кутта важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К.… … Википедия

Метод Рунге-Кутты — Методы Рунге Кутта важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К.… … Википедия

Метод Рунге — Куттa — Методы Рунге Кутта важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К.… … Википедия

метод Рунге-Кутта — Runge s ir Kutt o metodas statusas T sritis automatika atitikmenys: angl. Runge Kutta method vok. Runge Kutta Verfahren, n rus. метод Рунге Кутта, m pranc. méthode de Runge Kutta, f ryšiai: sinonimas – Rungės ir Kuto metodas … Automatikos terminų žodynas

Метод Эйлера — Метод Эйлера наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление»[1]. Метод Эйлера является явным, одношаговым методом… … Википедия

Метод Адамса — разностный метод численного интегрирования обыкновенных дифференциальных уравнений, позволяющий вычислять таблицу приближённых значений решения в начальных точках. Назван по имени предложившего его английского астронома Дж. К. Адамса в 1855.… … Википедия

Метод Гаусса (численное интегрирование) — Метод Гаусса метод численного интегрирования, позволяющий повысить алгебраический порядок точности методов на основе интерполяционных формул путём специального выбора узлов интегрирования без увеличения числа используемых значений подынтегральной … Википедия

Источник