для чего нужен логический квадрат
ЛОГИЧЕСКИЙ КВАДРАТ
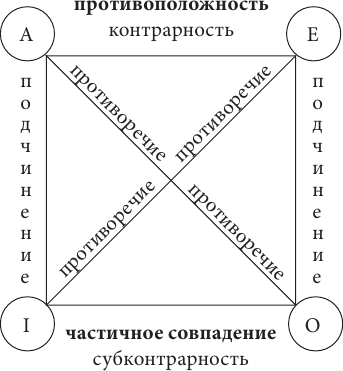
(квадрат противоположностей) – диаграмма, служащая для мнемонического запоминания некоторых логических соотношений между общеутвердительными (A), общеотрицательными (Е), частноутвердительными (I) и частноотрицательными суждениями (О). Логический квадрат показан на рисунке. Противоречащие, контрадикторные суждения (А и О; Е и I) не могут быть одновременно истинными и ложными: если одно из них истинно, то другое ложно. Так, если суждение «Все металлы являются электропроводными» (A) истинно, то суждение «Некоторые металлы не являются электропроводными» ложно. Если суждение «Некоторые металлы не являются твердыми» (О) истинно, то суждение «Все металлы являются твердыми» (А) ложно.
Противные суждения (A и Е), в отличие от противоречащих, могут оба оказаться ложными, но не могут быть оба истинными. Так, суждения «Все студенты являются шахматистами» (A) и «Ни один студент не является шахматистом» (Е) оба ложны. При истинности же одного из них второе является ложным. Так, если суждение «Все кенгуру являются млекопитающими» (A) истинно, то суждение «Ни один кенгуру не является млекопитающим» (Е) ложно. Подпротивные суждения (I и О) не могут быть одновременно ложными. Так, если суждение «Некоторые металлы не являются электропроводными» (О) ложно, то суждение «Некоторые металлы являются электропроводными» (I) (т. е. «Существуют металлы, которые электропроводны») является истинным. Подпротивные суждения могут оказаться и оба истинными. Таковы суждения «Некоторые металлы являются твердыми» (O)
и «Некоторые металлы не являются твердыми» (О).
Суждения, находящиеся в отношении подчинения (A, I и Е, О), отличаются, напр., тем важным свойством, что при истинности общих суждений соответствующие им частные также являются истинными. Так, истинность суждения «Все газы являются сжимаемыми» (A) влечет истинность подчиненного ему суждения (I) «Некоторые газы являются сжимаемыми».
2.9. Логический квадрат
2.9. Логический квадрат
Отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками.
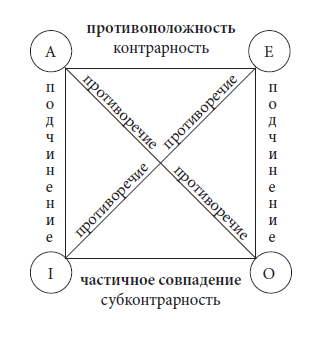
Как видим, вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения: Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, о которых идет речь в данном параграфе, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так если суждение вида А является истинным или ложным, то три других (I, Е, О) сравнимых с ним суждения (т. е. имеющих сходные с ним субъекты и предикаты) в зависимости от этого (т. е. от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: Все тигры – это хищники является истинным, то суждение вида I: Некоторые тигры – это хищники также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида Е: Все тигры – это не хищники является ложным, и суждение вида О: Некоторые тигры – это не хищники также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Далее представлены все случаи отношений между истинностными значениями простых сравнимых суждений.
1. Если суждение вида А является истинным, то суждение вида I также является истинным, а суждения вида Е и О являются ложными.
2. Если суждение вида А является ложным, то суждение вида I является неопределенным по истинности (т. е. может быть как истинным, так и ложным, в зависимости от того, о чем будет идти в нем речь), суждение вида Е является также неопределенным по истинности, а суждение вида О является истинным. (Далее будем применять сокращения, например, вместо выражения «суждение вида А» будем говорить «А», а вместо «является истинным» – просто «истинно»).
3. Если Е истинно, то А ложно, I ложно, О истинно.
4. Если Е ложно, то А неопределенно по истинности, I истинно, О неопределенно по истинности.
5. Если I истинно, то А неопределенно по истинности, Е ложно, О неопределенно по истинности.
6. Если I ложно, то А ложно, Е истинно, О истинно.
7. Если О истинно, то А ложно, Е неопределенно по истинности, I неопределенно по истинности.
8. Если О ложно, то А истинно, Е ложно, I истинно.
Используя рассмотренные правила, можно делать выводы об истинности простых сравнимых суждений с помощью логического квадрата (или, как часто говорят в логике, – по логическому квадрату). Выше был приведен пример таких выводов на основе суждения вида А: Все тигры являются хищниками, где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один пример. Возьмем суждение вида Е: Все треугольники не являются квадратами и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: Все треугольники являются квадратами ложно, суждение вида I: Некоторые треугольники являются квадратами также ложно, а суждение вида О: Некоторые треугольники не являются квадратами истинно (если все треугольники не являются квадратами, то и часть треугольников, т. е. некоторые треугольники также не являются ими).
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
IV. Квадрат коммуникации и генеративная матрица
Исторический и логический методы
Исторический и логический методы По большому счету эмпирический уровень научного познания сам по себе не достаточен для проникновения в сущность вещей, в том числе в закономерности функционирования и развития общества. На определенном этапе, когда накоплено уже более
Логический позитивизм Карнапа
Логический позитивизм Карнапа Логический позитивизм — это видоизмененная форма эмпиризма. Эмпиризм в чистом виде — это учение о том, что все знание мы получаем из чувственного опыта. Логический позитивизм выглядит слабее его в одном важном пункте, но зато сильнее в
Головоломный квадрат
Головоломный квадрат Изображенные на рисунке двадцать кругов образуют крест. Сколько квадратов можно найти в этом кресте, если считать, что любые четыре круга являются углами квадрата? Посмотрите на схему, и вы поймете, что имеется в виду. Четыре круга с буквой А
2. Логический позитивизм
2. Логический позитивизм В 1922 году на кафедре натуральной философии Венского университета, которую после смерти Э. Маха возглавил профессор М. Шлик, собралась группа молодых ученых, поставивших перед собой смелую цель — реформировать науку и философию. Эта группа вошла
Магический квадрат
Магический квадрат Предлагаем наимоднейший способ построить так называемый «магический квадрат». Из колоды игральных карт вытащите десять одной масти — от туза (примем его за единицу) до десятки — и сложите из них квадрат. Причем сложите так, чтобы сумма чисел на
Распили квадрат
Распили квадрат В один прекрасный день Пит Распил ввалился в кафе «Ложки и плошки» и сообщил всем о головоломке, которую только что услыхал от торговца древесиной. Тот показал Питу квадратную деревянную доску с маленьким отверстием в углу. «А теперь, — сказал торговец
2. Логический обвал
2. Логический обвал — То, что может быть продемонстрировано или что требуется доказать, есть конечное познание чего-то особенного. Экзистенция и трансценденция, в смысле этого бытия, не существуют. Если мы мыслим о них, то мысль принимает логические формы, которые
14. Тетрактис и квадрат четырех[119]
14. Тетрактис и квадрат четырех[119] В ходе наших исследований нам уже не раз случалось говорить о пифагорейском Тетрактисе, и мы тогда же привели его числовую формулу: 1+2+3+4=10, указав на связь, непосредственно соединяющую денер с кватернером. Известно совершенно особое
§ 4. Традиционный квадрат противопоставлений
§ 4. Традиционный квадрат противопоставлений Традиционное понимание противопоставления между суждениями отличается от предложенного нами понимания. Поскольку в традиционном подходе все суждения были разложимы на субъект и предикат, противопоставлялись только
ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ПАРАДОКС?
ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ПАРАДОКС? Никакого исчерпывающего перечня логических парадоксов не существует. Рассмотренные логические парадоксы – это только часть из всех обнаруженных к настоящему времени. Вполне вероятно, что в будущем будут открыты и многие другие
«Квадрат ресурсов»: ищите узел проблемы
«Квадрат ресурсов»: ищите узел проблемы Если вы затрудняетесь, какие пункты и этапы вам нужно обдумать, имеет смысл воспользоваться стандартной схемой «Четыре блока успеха: Люди, МТБ (материально-техническая база), Деньги и Время». Тут имеется в виду, что для любого
Логический позитивизм
Логический позитивизм В период между первой и второй мировыми войнами были выдвинуты новые философские идеи. Многие из них были стимулированы развитием неклассической физики и стали предметом серьезного эпистемологического анализа со стороны логического позитивизма.
15. ИНФИНИТЕЗИМАЛbНО–ЛОГИЧЕСКИЙ СЛОВАРb
15. ИНФИНИТЕЗИМАЛbНО–ЛОГИЧЕСКИЙ СЛОВАРb На этом мы закончим наше краткое сообщение о применении метода бесконечно–малых к логике. Вернее, это не сообщение, а только предложение, только скромный намек на ту область, которая не может не быть огромной. Логика и математика не
Возведение в квадрат и самоусиление
Возведение в квадрат и самоусиление Есть особенно интересный вид умножения, называемый возведением в квадрат, который дает нам подсказки относительно того, как работать с нашими собственными умами. Возведение в квадрат будет очень важно позднее, когда мы будем изучать
Перевоплощение и эксперимент возведения в квадрат
Перевоплощение и эксперимент возведения в квадрат Для начала вспомните недавнее сновидение. Затем выберите из этого сновидения какую-либо фигуру – человека, дерево или что угодно еще.Теперь представьте себе, что эта фигура – основа процесса, начало ее собственной
Логические отношения между суждениями (логический квадрат)
Основу отношений между суждениями составляет их сходство по смыслу и логическим значениям (истинности и ложности). В силу этого отношения устанавливаются не между любыми, а лишь между сравнимыми, т.е. имеющими общий смысл, суждениями.
Несравнимыми среди простых являются суждения, имеющие:
Таковы, например, два суждения:
«Среди космонавтов есть летчики »; «Среди космонавтов есть женщины ».
Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором (суждения одинаковой материи):
Среди сравнимых различают совместимые и несовместимые суждения.
Отношения между простыми суждениями обычно рассматриваются с помощью мнемонической схемы, называемой логическим квадратом.
Логический квадрат
Отношение совместимости
Виды совместимости:
Эквивалентные суждения имеют одинаковые логические характеристики:
С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются.
Различия между высказываниями, содержащими простые эквивалентные суждения, проявляются главным образом словесно.
Например, различными словами могут быть выражены кванторы: «некоторые», «иногда», «как правило» и т.п.; использованы синонимы для выражения субъекта или предиката; суждения могут быть сформулированы на различных национальных языках: «Это стол», «It is a table».
Эту особенность эквивалентных суждений надо учитывать при анализе правовых контекстов, при переводах с одного языка на другой, при сравнении словесно различных утверждений в процессе дискуссии.
Частичная совместимость характерна для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными.
При ложности одного из них другое будет истинным. Например, при ложности суждения «Некоторые злаки ядовиты» будет истинным суждение «Некоторые злаки не являются ядовитыми».
В то же время при истинности одного из частных суждений другое может быть как истинным, так и ложным.
Подчинение имеет место между суждениями А и I, E и О. Для них характерны следующие две зависимости:
Например, при истинности общего суждения «Всякое правоотношение регулируется нормами права» истинным будет и частное — «Некоторые правоотношения регулируются нормами права».
При истинности суждения «Ни один кооператив не относится к государственным организациям» будет истинным и суждение «Некоторые кооперативы не относятся к государственным организациям».
Например, если неверно утверждение, что «Некоторые хищения совершаются по неосторожности», то тем более будет неверным утверждение «Всякое хищение совершается по неосторожности».
При подчинении остаются неопределенными следующие зависимости:
Отношение несовместимости
Несовместимыми являются суждения
которые одновременно не могут быть истинными.
Виды несовместимости:
Противоположными (контрарными) являются суждения А и Е, которые одновременно
Истинность одного из противоположных суждений определяет ложность другого. Например, истинность суждения «Все офицеры — военнослужащие» определяет ложность суждения «Ни один офицер не является военнослужащим».
При ложности же одного из противоположных суждений другое остается неопределенным — оно может быть как истинным, так и ложным. Так, например, при ложности суждения «Все птицы улетают зимой в теплые края» ему противоположное «Ни одна птица не улетает зимой в теплые края» тоже оказывается ложным. В другом случае при ложности суждения «Ни один судья не является юристом» ему противоположное «Все судьи — юристы» будет истинным.
Для противоречия характерна строгая, или альтернативная несовместимость:
Отношения между такими суждениями регулируются законом исключенного третьего.
Например, если признается истинным суждение «Все принципиальные люди признают свои ошибки», то ложным будет ему альтернативное: «Некоторые принципиальные люди не признают своих ошибок».
Следует отметить, что несовместимые единичные суждения могут находиться лишь в отношении противоречия и не могут находиться в отношении противоположности, ибо каждому отдельному предмету может быть либо присущ, либо не присущ определенный признак.
Например, суждения «Суд вынес обвинительный приговор по делу Л.» и «Суд не вынес обвинительного приговора по делу Л.» находятся в отношении противоречия: если первое суждение истинно, то признается ложность второго, и наоборот.
Логический квадрат
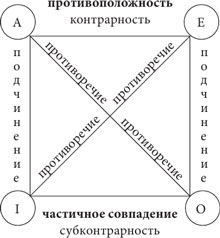
Наглядная схема, апеллируя к воображению человека, облегчает ему запоминание характера логических отношений между суждениями типа А, Е, I, O, в которых говорится об одном и том же, в то же время и в том же отношении. Истинность суждений об одном и том же, высказанных в одно и то же время, в одном и том же отношении и отличающихся друг от друга только по количеству и качеству, находится в формально-логической зависимости.
Происхождение квадрата может быть отнесено к Аристотелю, который впервые провел различие между двумя оппозициями: противоречия и противоположности. Но Аристотель не делал каких-либо схем. Теория была разработана спустя несколько веков Боэцием и Абеляром. Автором современного логического квадрата является византийский монах Михаил Пселл.
Концепцию логического квадрата разрабатывали такие философы и логики как Уильям из Шервуда, Роджер Бэкон, Жан Буридан, Джордж Буль, Питер Стросон.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
На эту страницу установлено перенаправление со страницы «A posteriori», см. также статью о музыкальном альбоме «A Posteriori».Апостерио́ри, а постерио́ри (лат. a posteriori букв. «из последующего») — знание, полученное из опыта. Противопоставляется априори — доопытному знанию. Значение термина исторически менялось: нынешнее значение установилось благодаря И. Канту и его работе «Критика чистого разума» (впервые опубликована в 1781 году, второе издание в 1787 г.) Однако, в латинской форме, выражения.
Деду́кция (лат. deductio — выведение, также дедуктивное умозаключение, силлогизм) — метод мышления, следствием которого является логический вывод, в котором частное заключение выводится из общего. Цепь умозаключений (рассуждений), где звенья (высказывания) связаны между собой логическими выводами.
Логический квадрат
Отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками.
Как видим, вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия.
Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т.е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: Все люди изучали логику и
Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения: Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, о которых идет речь в данном параграфе, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так если суждение вида А является истинным или ложным, то три других (I, Е, О) сравнимых с ним суждения (т. е. имеющих сходные с ним субъекты и предикаты) в зависимости от этого (т. е. от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: Все тигры – это хищники яляется истинным, то суждение вида I: Некоторые тигры – это хищники также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида Е: Все тигры – это не хищники является лож-ным, и суждение вида О: Некоторые тигры – это не хищники также является ложным.
Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Далее представлены все случаи отношений между истинностными значениями простых сравнимых суждений.
Используя рассмотренные правила, можно делать выводы об истинности простых сравнимых суждений с помощью логического квадрата (или, как часто говорят в логике, – по логическому квадрату). Выше был приведен пример таких выводов на основе суждения вида А: Все тигры являются хищниками, где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один при- мер.
Возьмем суждение вида Е: Все треугольники не являются квадратами и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: Все треугольники являются квадратами ложно, суждение вида I: Некоторые треугольники являются квадратами также лож- но, а суждение вида О: Некоторые треугольники не являются квадратами истинно (если все треугольники не являются квадратами, то и часть треугольников, т. е. некоторые треугольники также не являются ими).