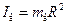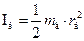для чего нужен маятник максвелла

Для чего нужен маятник максвелла

О, великий Максвелл! Однако маятник Максвелла не был им изобретен, а был только назван в его честь.
Это устройство используют для обучения школяров и студентов, им украшают оффисы, его дарят любознательным деткам. Идут годы, но только множатся всевозможные варианты этой научной игрушки!

Маятник Максвелла (иначе колесо Максвелла) известен как классическая иллюстрация превращения механической энергии.

Маятник состоит из диска, который закреплен на горизонтально оси, а ось подвешена с двух сторон на длинных нитях к опоре. Концы нитей закреплены на оси вращения. При накручивании нити на ось вращения и ее раскручивании маятник совершает колебательные движения вверх-вниз.

Для запуска маятника необходимо накрутить нити на ось, подняв таким образом маятник в наивысшую точку (потенциальная энергия здесь максимальна), а затем отпустить. Под действием силы тяжести маятник начнет опускаться вниз, все быстрее вращаясь, с постоянным ускорением.

Ускорение диска при его движении вниз не зависит от его массы и момента инерции, а зависит от соотношения радиуса оси вращения (r) и радиуса самого диска (R).

По мере движения вниз потенциальная энергия ранее поднятого маятника переходит в кинетическую энергию поступательного и вращательного движения. Опускания и подъемы диска со все уменьшающейся амплитудой повторяются много раз, пока маятник, наконец, не останавливается, т.к. весь первоначальный запас энергии в результате трения превращается в тепловую энергию.

В нижней точке траектории маятник за очень короткий промежуток времени меняет свое направление движения. Здесь нить маятника испытывает сильный рывок. Сила натяжения нити в этот момент возрастает в несколько раз. Эта дополнительная сила натяжения нити тем меньше, чем меньше радиус оси вращения, и тем больше, чем большее расстояние проходит маятник от начала движения до самой низшей точки. Если нить тонкая, то она может даже порваться.

Вместо обычного диска в маятнике Максвелла для вращения можно использовать и другие тела.

Так существует, например, физическая игрушка (есть и аналогичные ей), повторяющая принцип действия маятника Максвелла. Это разноцветный попугайчик, закрепленный, на оси вращения. Правда такая красивая игрушка приобретает и проблему. Фигурка не симметрична, поэтому конструктору требуется поразмыслить, как совместить центр тяжести попугайчика с центром вращения.

Точно по середине тонкой намагничивающейся хромированной оси насажен сильный магнит не очень большого диаметра. На магнит одевается пластиковая шайба-диск. Две хромированные железные штанги-направляющие (длиной около 50 см) закреплены на основании в вертикальном положении таким образом, что расстояние между ними внизу чуть больше длины оси с диском. К верху устройства расстояние между штангами слегка сужается.

Проследим, как работает этот маятник. Сначала надо симметрично приставить ось с диском к штангам вверху с одной или с другой стороны и отпустить ее. Притягиваясь к железу, намагниченная ось с диском под действием силы тяжести начинает сначала медленно, а затем все быстрее скатываться, вращаясь, по штангам вниз.

В зависимости от того, с какой стороны приставлена ось с диском к штангам, вращение диска будет вправо или влево. Возникшее в результате намагничивания притяжение оси к штангам обеспечивает не просто падение вниз, а вращение диска. Когда при скатывании диска вниз, расстояние между штангами становится чуть больше длины оси, то ось с диском проскакивает между штангами и попадает на их другую сторону. Сохранив направление вращения, диск, имеющий внизу максимальную скорость, проскальзывает между штангами на другую сторону и начинает подниматься вдоль них вверх.

Это изменение направления движения диска полностью соответствует принципу движения классического маятника Максвелла. Разница состоит лишь в том, что трение намагниченной оси о штанги в этом случае зависит от силы намагничивания. Она должна быть при выборе конструкции маятника строго рассчитана, чтобы ось с диском не сорвалась в самой нижней точке своего движения.
Всем, как говорится, хороши и маятник Максвелла, и Сизифов-маятник, одно плохо, покачавшись некоторое время, они все-таки останавливаются.

И тут интересен еще один вариант маятника, который волшебным способом будет крутиться, как покажется стороннему наблюдателю, сколько душе угодно! Он так и называется «волшебный маятник» (Magic rail twirler). Незаметные движения рук, и маятник никогда не остановится! Конечно, это шутка…

«Волшебный маятник» – это еще один вариант игрушки маятника Максвелла. В этом маятнике «легким нажатием руки» штанги можно раздвинуть, и диск поменяет направление своего движения. На хромированных направляющих штангах располагается диск с магнитной осью, концы которой часто выполнены в виде конусов. При работе игрушки очень хорошо видно, как меняется направление движения диска при увеличении расстояния между направляющими. Незаметным движением руки можно компенсировать потери энергии и достичь более многократного колебания диска вверх-вниз или из стороны в сторону. Более современные модели игрушек оснащены даже подсветкой изнутри диска.

Вот так имя великого физика соединило детскую научную игрушку и серьезный физический прибор.

Если захотите поэкспериментировать с маятником Максвелла, то сделать его в наше время не очень и трудно. Берете лазерный диск, скручиваете из листа школьной тетради трубочку и вставляете в центр диска. Трубочка слегка разворачивается и заполняет бумагой все отверстие. Отрезаете две одинаковые нити покрепче и капаете клеем, приклеивая нити к концам трубочки и центр диска к середине трубочки. Осталось подвесить….

А для детских умов знаменитый Я.И. Перельман загадал когда-то физическую загадку:
«Нити маятника Максвелла прикреплены к пружинному безмену.
Что должно происходить с указателем безмена в то время, когда диск-маховик исполняет свой танец вверх и вниз?
Останется ли указатель в покое?
Если будет двигаться, то в какую сторону?»

Если вам не удалось сразу отгадать, то ответ Перельмана таков:
«Когда диск опускается ускоренно вниз, чашка, к которой прикреплены нити, должна подниматься, так как освобождаемые нити не увлекают ее вниз с прежней силою.
Когда же диск-маховик поднимается замедленно вверх, то он натягивает наматывающиеся на его ось нитки, и они увлекают чашку вниз.
Короче говоря, чашка и привязанный к ней диск-маховик движутся навстречу друг к другу».
А вы как думали?

Источник: частично журн. «Physik in unserer Zeit».

Источник

МАЯТНИК МАКСВЕЛЛА

Цель работы: на основании законов динамики и сохранения механической энергии установить зависимость момента инерции маятника Максвелла, ускорений его поступательного и вращательного движений, определить зависимость энергии диссипации от числа колебаний маятника.

Рис.1

Маятник Максвелла представляет собой тело, способное совершать одновременно поступательное и вращательное движение (рис.1).

Поступательным движением твердого тела называется такое движение, при котором каждая линия, соединяющая две любые точки тела, сохраняет свое неизменное направление в пространстве. При поступательном движении тела прямая, проведенная через две произвольно выбранные точки этого тела, перемещается параллельно самой себе. Основы кинематики поступательного движения изложены в краткой теории к работе М1.

Основным законом динамики поступательного движения является торой закон Ньютона:

.

Вращательным движением твердого тела называется такое движение, при котором траектории всех точек тела являются концентрическими окружностями с центром на одной прямой, называемой осью вращения. Ось вращения может находиться вне тела или проходить через него. Основы кинематики и динамики вращательного движения в краткой теории к работам М1 и М3.

Рассмотрим более подробно закономерности поступательного и вращательного движения на приме маятника Максвелла, который представляет собой маховик, закрепленный на оси и подвешенный на двух нитях. Если нить намотать на ось маховика, то во время движения вниз она будет разматываться до полной длины. Раскрутившийся маховик продолжает вращательное движение в том же направлении и наматывает нить на ось, вследствие чего он поднимается вверх, замедляя при этом свое вращение. Дойдя до верхней точки, диск будет опять спускаться вниз и т.д. Маховик таким образом совершает колебания вверх и вниз и поэтому его называют маятником.

Движение всякой точки маятника мы можем представить как поступательное движение со скоростью , равной скорости центра инерции, и вращение вокруг оси с угловой скоростью w.

При движении на маятник действуют следующие силы и их моменты:

1) сила тяжести , приложенная к центру массы маятника и перпендикулярная оси вращения; момент силы тяжести равен нулю;

2) две силы натяжения нитей 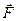, приложенные к мгновенным точкам соприкосновения нитей и валика; момент силы натяжения:

Запишем закон поступательного движения маятника, пренебрегая силами сопротивления:

Закон вращательного движения имеет вид:

или

Так как маятник Максвелла в процессе движения совершает равноускоренное движение с нулевой начальной скоростью, то изменение его скорости и координаты можно рассчитать по формулам:

Скорость центра инерции маятника (скорость оси маховика) и скорость вращения маятника связаны выражением

Существует связь и между ускорениями двух видов движения:

Решая совместно уравнения (1-6), можно получить необходимые для работы расчетные формулы:

Для определения моментов инерции используем формулу, выражающую закон сохранения механической энергии: потенциальная энергия маятника, находящегося в состоянии покоя на высоте h, равна кинетической энергии поступательного и вращательного движения маятника, находящегося в нижнем положении:

Учитывая формулу (5), находим:

С учетом (3-7) получим

Массу маятника надо определять по формуле

Вычисление теоретического момента инерции маятника

Вычисление теоретического момента инерции маятника производится путем определения моментов инерции отдельных его элементов (валик, диск, кольцо).

Все три предмета можно представить в виде правильных фигур. Значит формулы для вычисления их моментов инерции можно найти в справочных материалах.

Валик можно представить как кольцо с тонкими стенками (обруч):

Формула для расчета момента инерции диска:

Формула для расчета момента инерции кольца (с толстыми стенками):

Вычисление энергии диссипации

Записывая формулу (10), мы считали маятник консервативной системой. Однако неизбежно существует сопротивление, что приводит к рассеянию энергии. Благодаря этому, маятник не сможет снова подняться на высоту h. Часть механической энергии переходит в тепловую, т.е. происходит диссипация механической энергии. При малых скоростях диссипативные силы можно считать линейными функциями скоростей. Используя закон сохранения энергии, находим:

Таким образом

Числовое значение рассеивающейся энергии находим по формуле:

Вертикальная стойка имеет верхний и нижний кронштейны. На верхнем кронштейне имеется электромагнит, фотоэлектрический датчик и винт для закрепления и регулирования длины подвеса маятника. Нижний кронштейн вместе с прикрепленным к нему фотоэлектрическим датчиком можно перемещать вдоль стойки и фиксировать в выбранном положении.

На передней панели прибора находится:

1) выключатель сети «СЕТЬ». Для включения питания;

2) кнопка «СБРОС». Для обнуления секундомера;

3) управление электромагнитом «ПУСК». Нажатие этой клавиши выключает электромагнит и включает секундомер.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Определение динамических характеристик движения центра инерции маятника:

1) вычертите в тетради таблицу 1, помещенную в конце данных методических указаний;

2) взяв самое легкое кольцо, наденьте его на диск маятника; суммируйте массы кольца, диска и валика, результат запишите в таблицу;

3) нажмите на клавишу «СЕТЬ»;

4) намотайте на ось маятника нить так, чтобы витки располагались равномерно, при этом в своем верхнем положении маятник должен удерживаться электромагнитом;

5) нажмите на клавишу «СБРОС» (секундомер должен обнулиться);

6) при нажатии клавиши «ПУСК» маятник начнет движение вниз, а после достижения им нижнего фотоэлектрического датчика секундомер автоматически зафиксирует время опускания маятника с данной высоты;

7) измерение времени движения маятника выполнить 5 раз (показания секундомера записывайте в таблицу); высчитайте среднее значение и также внесите его в таблицу 1;

8) поменяйте кольцо на маятнике и повторите измерения согласно п.4-7;

9) повторите измерения и расчеты п. 4-7 для третьего кольца;

10) по шкале на вертикальной стойке определить путь, пройденный маятником и записать его в единицах системы СИ;

11) по формулам 7,8,9 и 11 рассчитайте ускорения поступательного и вращательного движения маятника, силу натяжения нитей и момент инерции маятника для всех трех колец. Результаты занесите в таблицу 1;

12) рассчитайте по формуле (12) теоретический момент инерции маятника для всех трех колец. Результаты запишите в таблицу и сравните со значениями I, рассчитанными ранее по формуле (11).

13) В заключении к работе сделать выводы о зависимости всех рассчитанных величин от массы маятника. Пояснить эти зависимости.

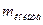, кг	, кг	t, с	tср, с	a, м/с 2	e, 1/с 2	F, Н	Iэ, кг×м 2	Iтеор, кг×м 2

Определение энергии диссипации

1. Вычертите в тетради таблицу 2, помещенную в конце данных методических указаний.

2. Произведите равномерное наматывание нити и закрепите маятник в верхнем положении.

3. Нажмите «ПУСК», приведите маятник в движение и зафиксируйте высоту h, с которой опускается центр инерции маятника и высоту его последующего поднятия h₁.

4. По формуле (12) вычислите силу сопротивления.

5. Произведите равномерное наматывание нити и закрепите маятник в верхнем положении.

6. Приведите маятник в движение, измерьте высоту в верхнем положении маятника после каждого из 10 колебаний.

7. Вычислите значение энергии диссипации по формуле (13).

8. Постройте график зависимости энергии диссипации от числа колебаний маятника.

9. В заключении к работе пояснить полученную зависимость W_d = f(n).

1. Как устроен маятник Максвелл?

2. Записать и прокомментировать уравнения поступательного и вращательного движения маятника.

3. Вывести формулу для расчета ускорения центра инерции маятника, углового ускорения маятника, силы натяжения нити, момента инерции маятника.

4 Записать закон сохранения энергии для маятника Максвелла и дать пояснения.

5. Что называется моментом инерции материальной точки и моментом инерции твердого тела? Единицы измерения этой величины.

6. Вывести формулу для определения силы сопротивления, действующей на маятник Максвелла.

7. Записать выражение для рассеивающейся энергии. Сделать пояснения.

Дата добавления: 2014-11-24 ; просмотров: 1824 ; Нарушение авторских прав

Источник

Маятник Максвелла

Цель работы: Определение момента инерции маятника.

Оборудование: маятник Максвелла типа ГРМ, комплект колец из трех штук.

Принцип работы основан на основном законе физики – законе сохранения энергии, который говорит, что механическая энергия замкнутой консервативной системы во время движения системы не изменяется. (Замкнутая – значит, нет внешних сил, совершающих работу и увеличивающих или уменьшающих механическую энергию системы; консервативная – нет диссипативных (трения, сопротивления и т. д.) сил, превращающих механическую энергию системы во внутреннюю (тепло).

Маятник Максвелла представляет

собой массивный диск, ось которого под-

вешена на двух накрученных на нее нитях.

Если маятник опустить, то под его тяжестью

нить будет раскручиваться, и он

начнет совершать возвратно-поступательные

движения в вертикальной плоскости при

одновременном вращении диска вокруг оси.

Движение всякой точки диска можно

представить как поступательное движение

со скоростью V, равной скорости центра

масс, и вращение вокруг геометрической

оси с угловой скоростью w. Полную скорость

любой точки получим, прибавив (векторно) к скорости

V` = w r, обусловленной вращением, скорость

поступательного движения V. В точке, где нить отделяется от оси, эта полная скорость равна нулю. Через эту точку проходит мгновенная ось вращения.

а кинетическая энергия всего тела

(1)

Введя в это выражение линейную скорость центра тяжести V = wr, получим

Полная кинетическая энергия плоского движения твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения вокруг оси, проходящей через центр тяжести.

По закону сохранения энергии в механике полная энергия Е изолированной системы, в которой действуют только упругие силы и силы всемирного тяготения, есть величина постоянная:

E = T + U = const

где U – потенциальная энергия.

В работе в начальный момент времени маятник находится в верхнем положении и обладает потенциальной энергией U. Кинетическая энергия Т = 0. Когда маятник опустится и пройдет путь h, то потенциальная энергия U1 = mgh перейдет в кинетическую энергию Т поступательного и вращательного движения Т2: U1 = Т2 или

(2)

Так как w = V/r, где r – радиус оси, на которую намотаны нити, то уравнение (2) принимает вид:

(3)

Движение маятника равноускоренное, следовательно, можно применить следующие формулы для пути и скорости:

h = Vot + at2/2

В работе начальная скорость Vo = 0, тогда

h = at2/2

V = at

Из этой системы уравнений находим:

Подставим полученное значение V в уравнение (3):

(4)

Эту же формулу можно получить другим

способом. На диск массы m действуют сила тяже-

сти mg и натяжений нитей f. Ускорение а центра

тяжести диска определяется уравнением:

Ось моментов выберем так, чтобы она про-

ходила через центр тяжести диска (т. е. совпадала

с его геометрической осью О). Момент силы тяже-

сти относительно этой оси равен нулю, а момент

тона для вращательного движения маятника имеет вид:

Из уравнения (5) найдем:

Подставив (7) в (8), получим:

Ускорение а найдем из формулы пройденного пути маятника h:

и подставив в уравнение (7), получим

Это выражение аналогично формуле (4). Поскольку диаметр легче измерить, чем радиус, заменим r на 0,5d и получим окончательно такую формулу для Io :

(9)

Здесь Io – момент инерции маятника, m – масса маятника, d – диаметр валика, на который наматываются нити, g – ускорение свободного падения, h – расстояние, пройденное центром маятника за время t.

Теперь уточним значение массы m и диаметра d. В данной работе маятник Максвелла представляет собой ось с валиками, на которые плотно насаживается съемное кольцо:

mo – масса оси маятника, mк – масса кольца, mр – масса валика (ролика)

где do – внешний диаметр оси маятника, dн – диаметр нити подвески.

Измерения

Подготовка к измерениям: Чтобы подготовить прибор к работе, необходимо:

— привести прибор в горизонтальное положение при помощи регулируемых ножек основания

— включить сетевой шнур измерителя в питающую сеть

— нажать клавишу «СЕТЬ», проверяя, все ли индикаторы измерителя высвечивают цифру нуль и засветились ли лампочки обоих фотоэлектрических датчиков.

Прибор готов к работе непосредственно после включения сетевого напряжения и не нуждается в прогреве.

Измерение момента инерции маятника

На ролик маятника заложить выбранное кольцо, прижимая его до упора.

На ось маятника намотать нить подвески и зафиксировать ее.

Проверить, отвечает ли нижняя грань кольца нулю шкалы на колонке. Если нет, отвинтить верхний кронштейн и отрегулировать его высоту. Привинтить верхний кронштейн.

Нажать клавишу «ПУСК» миллисекундомера.

Деблокировать гайку ворота для регулирования длины нити таким образом, чтобы край стального кольца после опускания маятника находился около 2 мм ниже оптической оси нижнего фотоэлектрического датчика. Одновременно произвести коррекцию установки маятника, обращая внимание на то, чтобы его ось была параллельной основанию прибора. Блокировать вороток.

Отжать клавишу «ПУСК» миллисекундомера.

Намотать на ось маятника нить подвески, обращая внимание на то, чтобы она наматывалась равномерно, один виток рядом с другим.

Фиксировать маятник при помощи электромагнита, обращая внимание на то, чтобы нить в этом положении не была слишком скручена.

Повернуть маятник в направлении его движения на угол около 5о.

Нажать клавишу «СБРОС».

Нажать клавишу «ПУСК».

Прочитать и записать измеренное значение времени падения маятника.

Определить замер времени 5 раз.

Определить значение среднего времени падения маятника по формуле:

(12)

где n – количество выполненных замеров, ti – значение времени, полученное в i – том замере, t – среднее значение времени падения маятника.

По шкале на вертикальной колонке прибора определить расстояние, проходимое маятником за время падения.

По формуле (10) вычислить массу маятника вместе с кольцом, наложенным в данном опыте. Значения масс отдельных элементов нанесены на них.

По формуле (9) определить момент инерции маятника.

Сравнить с теоретическим значением момента инерции

Проделать аналогичные измерения и сравнение с теорией для двух других колец.

В отчете должны быть приведены полученные экспериментально и теоретически вычисленные значения трех моментов инерций с определенными погрешностями результатов (как экспериментальных, так и теоретических).

1. Что называется моментом инерции? Формула для моментов инерции сплошного диска, цилиндра, кольца.

2. Что называется моментом силы?

3. Сформулируйте теорему Гюйгенса-Штейнера.

4. Что такое маятник Максвелла? Почему он называется маятником?

5. Что такое механическая энергия движущегося и вращающегося твердого тела? В каком случае механическая энергия тела сохраняется?

Источник