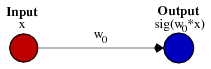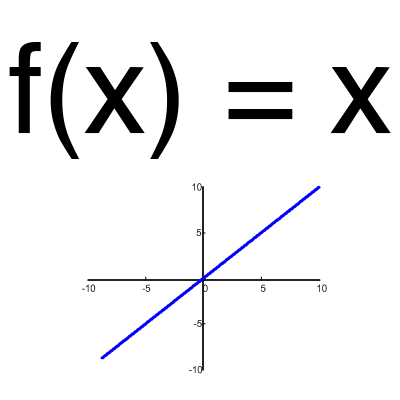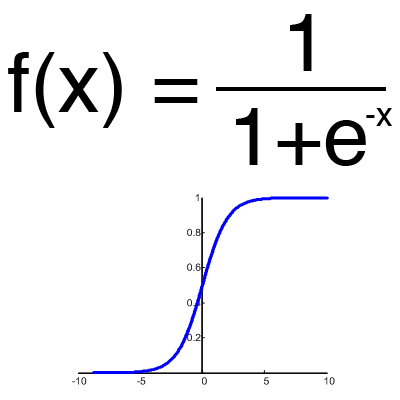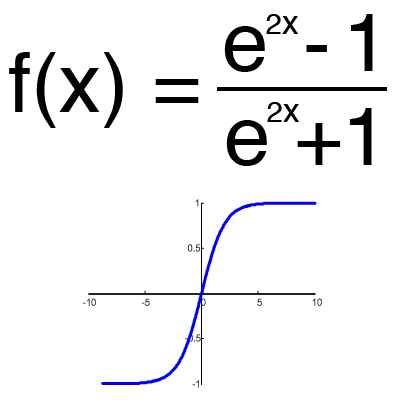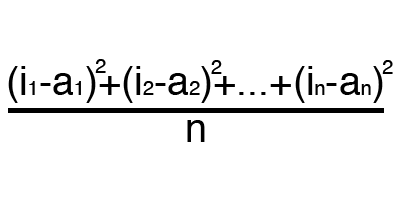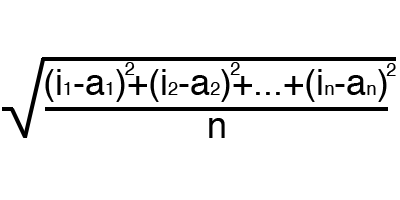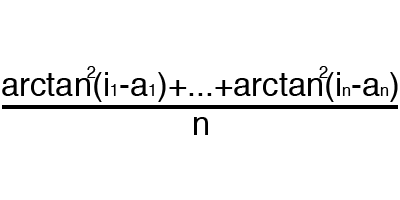для чего нужен нейрон смещения
Нейронные сети. (Machine learning #1)
Что такое нейронная сеть и как она работает? Разбираем популярную технологию на простых примерах!
Сайту исполняется год и в честь этого я решил написать небольшой пост о том, чем я сейчас занимаюсь 🙂
Однажды, гуляя по просторам YouTube, я наткнулся на очень классный канал, посвященный математике, физике и многим другим интересным вещам (даже радиоэлектронике!) На канале было очень много всего, чего я не успел пока посмотреть, но я обратил внимание на ролик, посвященный работе нейронных сетей. Так как я давно уже слышал о нейронных сетях и похожих вещах (вроде генетических алгоритмов), но при этом не понимал толком, о чём идёт речь, я очень заинтересовался. Это цикл из 4х видео, которые, по сути, являются визуализацией статьи Michael Nielsen.
Здесь я хочу дать краткое и простое описание работы нейронной сети на примере классической задачи распознавания нарисованных от руки цифр.
Итак, представьте, что перед вами встала задача распознать цифры:
Наш мозг без труда справляется с такой задачей! Но что, если у нас есть миллион написанных от руки цифр, которые необходимо распознать и записать, допустим, в базу данных. Нужно написать программу, которая будет делать это за вас.
Но как будет работать такая программа? И тут задача, которая казалась пустяковой, превратилась в большую проблему: каждый человек пишет одни и те же цифры по-разному, а компьютер этого не знает. Вот, например, написанная по-разному, цифра 5:
Понятие нейрона, веса и смещения
Давайте рассмотрим простую нейронную сеть:
Запишем сумму со всех нейронов из входного слоя:
$$
z = \sum\limits_
$$
Получившийся результат может быть любым вещественным числом. Нам нужно преобразовать его в число от 0 до 1, которое мы и присвоим нейрону.
Сделать это можно, например, так:
Видно, что рост функции от нуля до единицы происходит в окрестности нуля. Но часто активационный барьер необходимо сместить. Поэтому к числу \(z \) в (1) нужно прибавить число \(b \), которое называется смещением (bias). То есть
$$
z = \sum\limits_
$$
Для всего слоя (в матричном виде):
Как происходит обучение?
Картинка \(28*28 \) содержит \(784 \) пикселя, именно столько и будет нейронов в входном слое.
В выходном слое будет 10 нейронов, каждый из которых указывает на цифру от \(0\) до \(9\). Для упрощения понимания изобразим лишь один скрытый слой. По выходному слою мы будем судить о том, как отработал алгоритм.
Как и было сказано ранее, работа алгоритма полностью определяется входными данными и взаимосвязями нейронов. Когда алгоритм не натренирован, то, скорее всего, он не сможет дать правильный ответ, так как взаимосвязи между нейронами (веса нейронов и смещения) настроены неправильно. Именно в подборе этих параметров и заключается обучение нейронной сети.
Теперь дадим нашей сети группу картинок с написанными цифрами для тренировки и после каждого завершения алгоритма будем проверять то, насколько точно она «угадала» цифру.
Для того, чтобы оценить эффективность работы алгоритма, введём так называемую функцию расходимости (cost function) следующим образом:
Чем ближе результат работы алгоритма к требуемому результату, тем меньше становится функция расхождения. То есть задача обучения на данном этапе сводится к уменьшению функции расхождения.
Как нужно изменять все \(w\) и \(b\), чтобы максимально быстро уменьшить функцию расхождения?
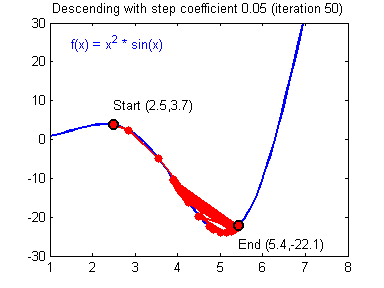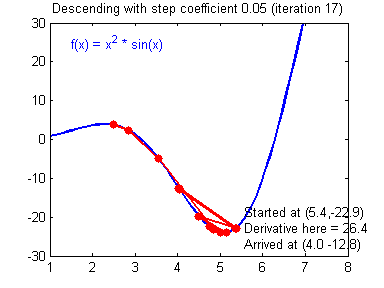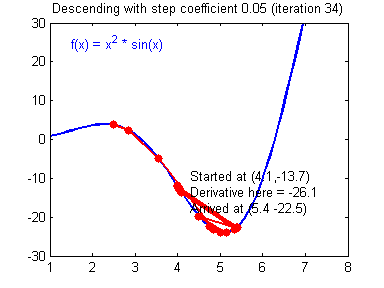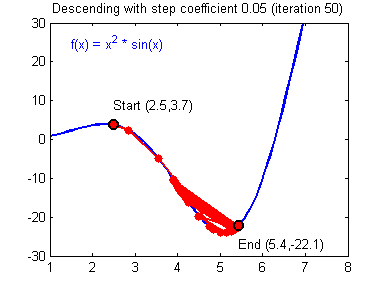
Нужно найти вектор-градиент функции и идти в противоположную сторону. Если бы наша сеть имела только одно смещение \(b\) и один вес \(w\), то данный процесс можно было бы проиллюстрировать мячом, скатывающимся в самую нижнюю точку ямки:
$$
\frac<\partial C(w, b)> <\partial y_t>= \frac<1><2l>2y_t = \frac
$$
А производная
$$
\frac<\partial y_t(x_
$$
легко считается, так как у нас есть явный вид функции \(y_t\) от \(w_i\) в (5).
Теперь разберёмся с производными \(С(w, b)\) по смещениям \(b\). Расчёт производится аналогично:
В принципе, это все! Весь процесс обучения взял на себя компьютер, который считает частные производные функции расхождения и с их помощью правильно корректирует параметры связей нейронов.
Однако, как я понял, чаще всего вычисляют не все частные производные (в нашем случае их \(12719\)), а только часть, разделяя параметры на небольшие группы. Такой подход называется stochastic gradient descent, и он быстрее приводит к нужному результату, так как на вычисление всех частных производных тратится большее время.
Можете похлопать себя по плечам, ведь выше прочитанный материал не из простых и требует усилия для усвоения!
Это не последний мой пост, посвященный нейронным сетям и машинному обучению. У меня есть несколько крутых проектов, связанных с этой темой, которые я хочу реализовать и более глубоко раскрыть в следующих моих статьях.
Отдельная благодарность моей сестре Соне (отличному репетитору по русскому языку) за час смеха и мучения при правке статьи!
Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.
Нейронные сети для начинающих. Часть 1
Привет всем читателям Habrahabr, в этой статье я хочу поделиться с Вами моим опытом в изучении нейронных сетей и, как следствие, их реализации, с помощью языка программирования Java, на платформе Android. Мое знакомство с нейронными сетями произошло, когда вышло приложение Prisma. Оно обрабатывает любую фотографию, с помощью нейронных сетей, и воспроизводит ее с нуля, используя выбранный стиль. Заинтересовавшись этим, я бросился искать статьи и «туториалы», в первую очередь, на Хабре. И к моему великому удивлению, я не нашел ни одну статью, которая четко и поэтапно расписывала алгоритм работы нейронных сетей. Информация была разрознена и в ней отсутствовали ключевые моменты. Также, большинство авторов бросается показывать код на том или ином языке программирования, не прибегая к детальным объяснениям.
Поэтому сейчас, когда я достаточно хорошо освоил нейронные сети и нашел огромное количество информации с разных иностранных порталов, я хотел бы поделиться этим с людьми в серии публикаций, где я соберу всю информацию, которая потребуется вам, если вы только начинаете знакомство с нейронными сетями. В этой статье, я не буду делать сильный акцент на Java и буду объяснять все на примерах, чтобы вы сами смогли перенести это на любой, нужный вам язык программирования. В последующих статьях, я расскажу о своем приложении, написанном под андроид, которое предсказывает движение акций или валюты. Иными словами, всех желающих окунуться в мир нейронных сетей и жаждущих простого и доступного изложения информации или просто тех, кто что-то не понял и хочет подтянуть, добро пожаловать под кат.
Первым и самым важным моим открытием был плейлист американского программиста Джеффа Хитона, в котором он подробно и наглядно разбирает принципы работы нейронных сетей и их классификации. После просмотра этого плейлиста, я решил создать свою нейронную сеть, начав с самого простого примера. Вам наверняка известно, что когда ты только начинаешь учить новый язык, первой твоей программой будет Hello World. Это своего рода традиция. В мире машинного обучения тоже есть свой Hello world и это нейросеть решающая проблему исключающего или(XOR). Таблица исключающего или выглядит следующим образом:
| a | b | c |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Соответственно, нейронная сеть берет на вход два числа и должна на выходе дать другое число — ответ. Теперь о самих нейронных сетях.
Что такое нейронная сеть?
Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами. Структура нейронной сети пришла в мир программирования прямиком из биологии. Благодаря такой структуре, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Заинтересовавшимся обязательно к просмотру 2 видео из TED Talks: Видео 1, Видео 2). Другими словами, нейросеть это машинная интерпретация мозга человека, в котором находятся миллионы нейронов передающих информацию в виде электрических импульсов.
Какие бывают нейронные сети?
Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.
Для чего нужны нейронные сети?
Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:
Классификация — распределение данных по параметрам. Например, на вход дается набор людей и нужно решить, кому из них давать кредит, а кому нет. Эту работу может сделать нейронная сеть, анализируя такую информацию как: возраст, платежеспособность, кредитная история и тд.
Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.
Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.
Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.
Что такое нейрон?
Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый). Также есть нейрон смещения и контекстный нейрон о которых мы поговорим в следующей статье. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат. У каждого из нейронов есть 2 основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.
Важно помнить, что нейроны оперируют числами в диапазоне [0,1] или [-1,1]. А как же, вы спросите, тогда обрабатывать числа, которые выходят из данного диапазона? На данном этапе, самый простой ответ — это разделить 1 на это число. Этот процесс называется нормализацией, и он очень часто используется в нейронных сетях. Подробнее об этом чуть позже.
Что такое синапс?
Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.
Важно помнить, что во время инициализации нейронной сети, веса расставляются в случайном порядке.
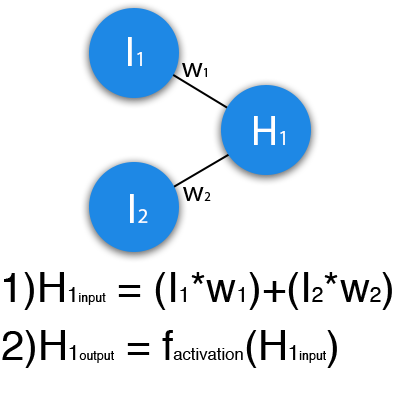
Как работает нейронная сеть?
В данном примере изображена часть нейронной сети, где буквами I обозначены входные нейроны, буквой H — скрытый нейрон, а буквой w — веса. Из формулы видно, что входная информация — это сумма всех входных данных, умноженных на соответствующие им веса. Тогда дадим на вход 1 и 0. Пусть w1=0.4 и w2 = 0.7 Входные данные нейрона Н1 будут следующими: 1*0.4+0*0.7=0.4. Теперь когда у нас есть входные данные, мы можем получить выходные данные, подставив входное значение в функцию активации (подробнее о ней далее). Теперь, когда у нас есть выходные данные, мы передаем их дальше. И так, мы повторяем для всех слоев, пока не дойдем до выходного нейрона. Запустив такую сеть в первый раз мы увидим, что ответ далек от правильно, потому что сеть не натренирована. Чтобы улучшить результаты мы будем ее тренировать. Но прежде чем узнать как это делать, давайте введем несколько терминов и свойств нейронной сети.
Функция активации
Функция активации — это способ нормализации входных данных (мы уже говорили об этом ранее). То есть, если на входе у вас будет большое число, пропустив его через функцию активации, вы получите выход в нужном вам диапазоне. Функций активации достаточно много поэтому мы рассмотрим самые основные: Линейная, Сигмоид (Логистическая) и Гиперболический тангенс. Главные их отличия — это диапазон значений.
Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.
Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.
Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции [-1,1]. Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.
Тренировочный сет
Тренировочный сет — это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1,1xor1=0.
Итерация
Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть проходит один тренировочный сет. Другими словами, это общее количество тренировочных сетов пройденных нейронной сетью.
Эпоха
При инициализации нейронной сети эта величина устанавливается в 0 и имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована сеть и соответственно, ее результат. Эпоха увеличивается каждый раз, когда мы проходим весь набор тренировочных сетов, в нашем случае, 4 сетов или 4 итераций.
Важно не путать итерацию с эпохой и понимать последовательность их инкремента. Сначала n
раз увеличивается итерация, а потом уже эпоха и никак не наоборот. Другими словами, нельзя сначала тренировать нейросеть только на одном сете, потом на другом и тд. Нужно тренировать каждый сет один раз за эпоху. Так, вы сможете избежать ошибок в вычислениях.
Ошибка
Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка формируется каждую эпоху и должна идти на спад. Если этого не происходит, значит, вы что-то делаете не так. Ошибку можно вычислить разными путями, но мы рассмотрим лишь три основных способа: Mean Squared Error (далее MSE), Root MSE и Arctan. Здесь нет какого-либо ограничения на использование, как в функции активации, и вы вольны выбрать любой метод, который будет приносить вам наилучший результат. Стоит лишь учитывать, что каждый метод считает ошибки по разному. У Arctan, ошибка, почти всегда, будет больше, так как он работает по принципу: чем больше разница, тем больше ошибка. У Root MSE будет наименьшая ошибка, поэтому, чаще всего, используют MSE, которая сохраняет баланс в вычислении ошибки.
Принцип подсчета ошибки во всех случаях одинаков. За каждый сет, мы считаем ошибку, отняв от идеального ответа, полученный. Далее, либо возводим в квадрат, либо вычисляем квадратный тангенс из этой разности, после чего полученное число делим на количество сетов.
Задача
Теперь, чтобы проверить себя, подсчитайте результат, данной нейронной сети, используя сигмоид, и ее ошибку, используя MSE.
H1input = 1*0.45+0*-0.12=0.45
H1output = sigmoid(0.45)=0.61
H2input = 1*0.78+0*0.13=0.78
H2output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
Результат — 0.33, ошибка — 45%.
Большое спасибо за внимание! Надеюсь, что данная статья смогла помочь вам в изучении нейронных сетей. В следующей статье, я расскажу о нейронах смещения и о том, как тренировать нейронную сеть, используя метод обратного распространения и градиентного спуска.
Роль смещения в нейронных сетях
Я знаю о градиентном спуске и теореме обратного распространения. Что я не понимаю: когда важно использовать предвзятость и как вы ее используете?
например, при отображении AND функция, когда я использую 2 входа и 1 выход, он не дает правильные веса, однако, когда я использую 3 входа (1 из которых является смещением), он дает правильные веса.
16 ответов
Я думаю, что предубеждения почти всегда полезны. В сущности,значение смещения позволяет смещать функцию активации влево или вправо, которые могут иметь решающее значение для успешного обучения.
Это может помочь взглянуть на простой пример. Рассмотрим эту 1-входную, 1-выходную сеть, которая не имеет смещения:
выход сети вычисляется путем умножения входного сигнала (x) на вес (w0) и прохождения результат через некоторую функцию активации (например, сигмовидную функцию.)
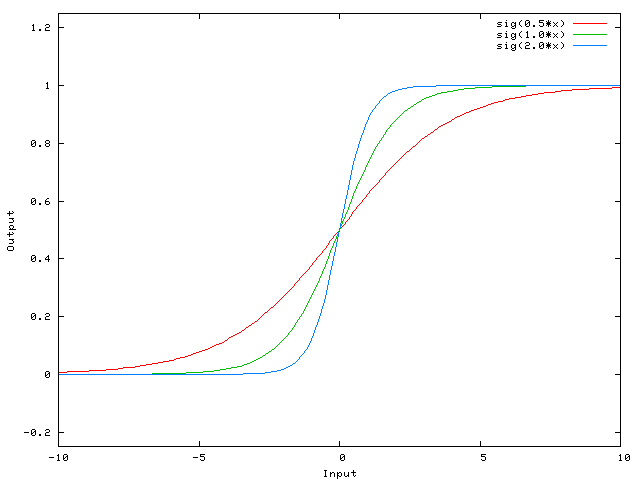
вот функция, которую вычисляет эта сеть, для различных значений w0:
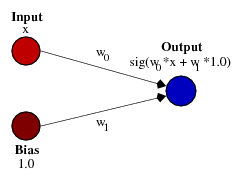
Это именно то, что позволяет вам делать смещение. Если мы добавим смещение к этой сети, например:
. тогда выход сети становится sig(w0 * x + w1*1.0). Вот как выглядит выход сети для различных значений w1:
просто добавить мои два цента.
более простой способ понять, что такое смещение: оно как-то похоже на константу b линейной функции
Это позволяет перемещать линию вверх и вниз, чтобы лучше соответствовать прогнозу с данными. Без b линия всегда проходит через начало координат (0, 0), и вы можете сделать более пригодный.
2 различных вида параметров могут отрегулируйте во время тренировки Энн, веса и значение в функция активации. Это непрактично и было бы легче, если бы только один из параметров должен быть отрегулированный. Чтобы справиться с этой проблемой изобретен нейрон смещения. Предвзятость нейрон лежит в одном слое, соединен всем нейронам в следующем слое, но нет в предыдущем слое и это всегда выдает 1. С момента смещения нейрона выдает 1 весы, связанные с нейрон смещения, добавлены сразу к совокупность других Весов (уравнение 2.1), Как и значение t в функциях активации.1
причина, по которой это непрактично, заключается в том, что вы одновременно регулируете вес и значение, поэтому любое изменение веса может нейтрализовать изменение значения, которое было полезно для предыдущего экземпляра данных. добавление нейрона смещения без изменения значения позволяет контролируйте поведение слоя.
кроме того, смещение позволяет использовать одну нейронную сеть для представления подобных случаев. Рассмотрим и булеву функцию, представленную следующей нейронной сетью:
одиночный персептрон можно использовать к представляют множество булевых функций.
перцептронов может представлять все примитивные булевы функции и, или, NAND (1 и), и NOR ( 1 или). Машинное Обучение-Том Митчелл)
Это означает, что вы используете линейную функцию и, таким образом, вход всех нулей всегда будет отображаться на выход всех нулей. Это может быть разумным решением для некоторых систем, но в целом это слишком ограничительный.
используя смещение, вы эффективно добавляете другое измерение к своему входному пространству, которое всегда принимает значение one, поэтому вы избегаете входного вектора всех нулей. Вы не теряете общности, потому что ваша обученная матрица веса не должна быть сюръективной, поэтому она все еще может сопоставляться со всеми ранее возможными значениями.
2d ANN:
для отображения ANN двух измерений в одно измерение, как при воспроизведении AND или OR (или XOR) функции, вы можете думать о нейронной сети, как делать следующее:
на 2d плоскости отметьте все позиции входных векторов. Так, для логических значений, вы захотите пометить (-1,-1), (1,1), (-1,1), (1,-1). Теперь ваша ANN рисует прямую линию на 2d-плоскости, отделяя положительные выходные данные от отрицательных выходных значений.
без смещения эта прямая линия должна пройти через ноль, тогда как с смещением вы можете поместить ее куда угодно. Итак, вы увидите, что без смещения вы сталкиваетесь с проблемой с функцией AND, так как вы не можете поставить оба (1,-1) и (-1,1) в отрицательную сторону. (Им не позволено быть on линии.) Проблема равна для функции OR. С уклоном, однако, легко провести черту.
обратите внимание, что функция XOR в этой ситуации не может быть решена даже с уклоном.
когда вы используете ANNs, вы редко знаете о внутренних системах, которые вы хотите узнать. Некоторые вещи нельзя узнать без предубеждения. Например, взгляните на следующие данные: (0, 1), (1, 1), (2, 1), в основном функция, которая отображает любой x в 1.
Если у вас есть однослойная сеть (или линейное отображение), вы не можете найти решение. Однако, если у вас есть предубеждение, это тривиально!
в идеальной обстановке смещение может также сопоставлять все точки со средним значением цели точки и пусть скрытые нейроны моделируют различия с этой точки.
смещение не NN термин, это общий термин алгебры для рассмотрения.
Вам наверняка известно, что когда ты только начинаешь учить новый язык, первой твоей программой будет Hello World. Это своего рода традиция. В мире машинного обучения тоже есть свой Hello world и это нейросеть решающая проблему исключающего или(XOR). Таблица исключающего или выглядит следующим образом:
| a | b | c |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Соответственно, нейронная сеть берет на вход два числа и должна на выходе дать другое число — ответ. Теперь о самих нейронных сетях.
Что такое нейронная сеть?
Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами. Структура нейронной сети пришла в мир программирования прямиком из биологии. Благодаря такой структуре, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Заинтересовавшимся обязательно к просмотру 2 видео из TED Talks: Видео 1, Видео 2). Другими словами, нейросеть это машинная интерпретация мозга человека, в котором находятся миллионы нейронов передающих информацию в виде электрических импульсов.
Какие бывают нейронные сети?
Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.
Для чего нужны нейронные сети?
Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:
Классификация — распределение данных по параметрам. Например, на вход дается набор людей и нужно решить, кому из них давать кредит, а кому нет. Эту работу может сделать нейронная сеть, анализируя такую информацию как: возраст, платежеспособность, кредитная история и тд.
Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.
Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.
Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.
Что такое нейрон?
Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый). Также есть нейрон смещения и контекстный нейрон о которых мы поговорим в следующей статье. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат. У каждого из нейронов есть 2 основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.
Важно помнить, что нейроны оперируют числами в диапазоне [0,1] или [-1,1]. А как же, вы спросите, тогда обрабатывать числа, которые выходят из данного диапазона? На данном этапе, самый простой ответ — это разделить 1 на это число. Этот процесс называется нормализацией, и он очень часто используется в нейронных сетях. Подробнее об этом чуть позже.
Что такое синапс?
Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.
Важно помнить, что во время инициализации нейронной сети, веса расставляются в случайном порядке.
Как работает нейронная сеть?
В данном примере изображена часть нейронной сети, где буквами I обозначены входные нейроны, буквой H — скрытый нейрон, а буквой w — веса. Из формулы видно, что входная информация — это сумма всех входных данных, умноженных на соответствующие им веса. Тогда дадим на вход 1 и 0. Пусть w1=0.4 и w2 = 0.7 Входные данные нейрона Н1 будут следующими: 1*0.4+0*0.7=0.4. Теперь когда у нас есть входные данные, мы можем получить выходные данные, подставив входное значение в функцию активации (подробнее о ней далее). Теперь, когда у нас есть выходные данные, мы передаем их дальше. И так, мы повторяем для всех слоев, пока не дойдем до выходного нейрона. Запустив такую сеть в первый раз мы увидим, что ответ далек от правильно, потому что сеть не натренирована. Чтобы улучшить результаты мы будем ее тренировать. Но прежде чем узнать как это делать, давайте введем несколько терминов и свойств нейронной сети.
Функция активации
Функция активации — это способ нормализации входных данных (мы уже говорили об этом ранее). То есть, если на входе у вас будет большое число, пропустив его через функцию активации, вы получите выход в нужном вам диапазоне. Функций активации достаточно много поэтому мы рассмотрим самые основные: Линейная, Сигмоид (Логистическая) и Гиперболический тангенс. Главные их отличия — это диапазон значений.
Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.
Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.
Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции [-1,1]. Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.
Тренировочный сет
Тренировочный сет — это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1,1xor1=0.
Итерация
Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть проходит один тренировочный сет. Другими словами, это общее количество тренировочных сетов пройденных нейронной сетью.
Эпоха
При инициализации нейронной сети эта величина устанавливается в 0 и имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована сеть и соответственно, ее результат. Эпоха увеличивается каждый раз, когда мы проходим весь набор тренировочных сетов, в нашем случае, 4 сетов или 4 итераций.
Важно не путать итерацию с эпохой и понимать последовательность их инкремента. Сначала n
раз увеличивается итерация, а потом уже эпоха и никак не наоборот. Другими словами, нельзя сначала тренировать нейросеть только на одном сете, потом на другом и тд. Нужно тренировать каждый сет один раз за эпоху. Так, вы сможете избежать ошибок в вычислениях.
Ошибка
Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка формируется каждую эпоху и должна идти на спад. Если этого не происходит, значит, вы что-то делаете не так. Ошибку можно вычислить разными путями, но мы рассмотрим лишь три основных способа: Mean Squared Error (далее MSE), Root MSE и Arctan. Здесь нет какого-либо ограничения на использование, как в функции активации, и вы вольны выбрать любой метод, который будет приносить вам наилучший результат. Стоит лишь учитывать, что каждый метод считает ошибки по разному. У Arctan, ошибка, почти всегда, будет больше, так как он работает по принципу: чем больше разница, тем больше ошибка. У Root MSE будет наименьшая ошибка, поэтому, чаще всего, используют MSE, которая сохраняет баланс в вычислении ошибки.
Принцип подсчета ошибки во всех случаях одинаков. За каждый сет, мы считаем ошибку, отняв от идеального ответа, полученный. Далее, либо возводим в квадрат, либо вычисляем квадратный тангенс из этой разности, после чего полученное число делим на количество сетов.
Задача
Теперь, чтобы проверить себя, подсчитайте результат, данной нейронной сети, используя сигмоид, и ее ошибку, используя MSE.
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
Результат — 0.33, ошибка — 45%.
Большое спасибо за внимание! Надеюсь, что данная статья смогла помочь вам в изучении нейронных сетей. В следующей статье, я расскажу о нейронах смещения и о том, как тренировать нейронную сеть, используя метод обратного распространения и градиентного спуска.
Что такое нейрон смещения?
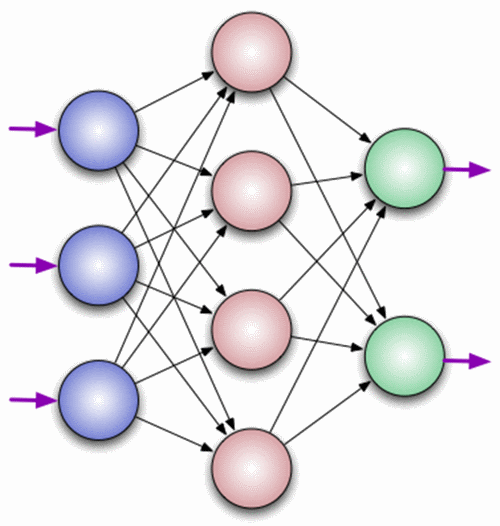
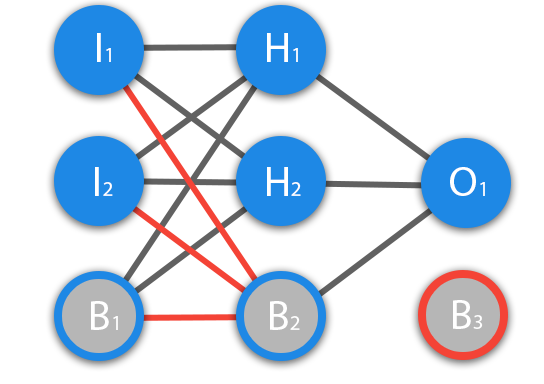
Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь.
Для чего нужен нейрон смещения?

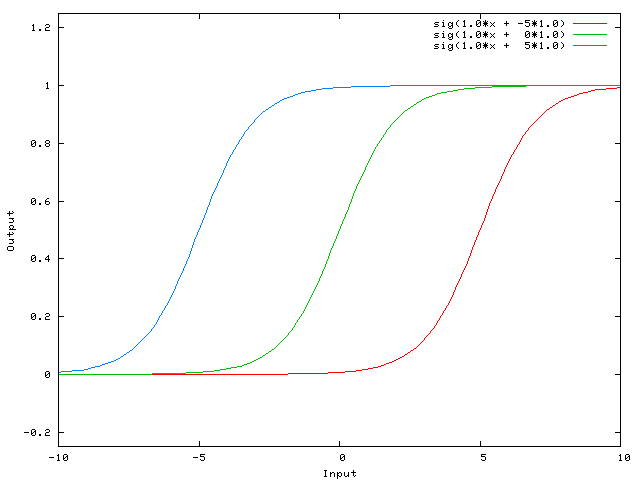
Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу H1, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.
Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес H1, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.
Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.
ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:
input = H1*w1+H2*w2+b3
b3 = bias*w3
Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.
Как сделать чтобы НС давала правильные ответы?
Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:
Об Rprop и ГА речь пойдет в других статьях, а сейчас мы с вами посмотрим на основу основ — метод обратного распространения, который использует алгоритм градиентного спуска.
Что такое градиентный спуск?
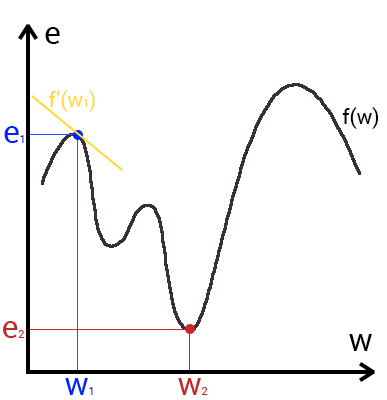
Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e).
Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.
Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:
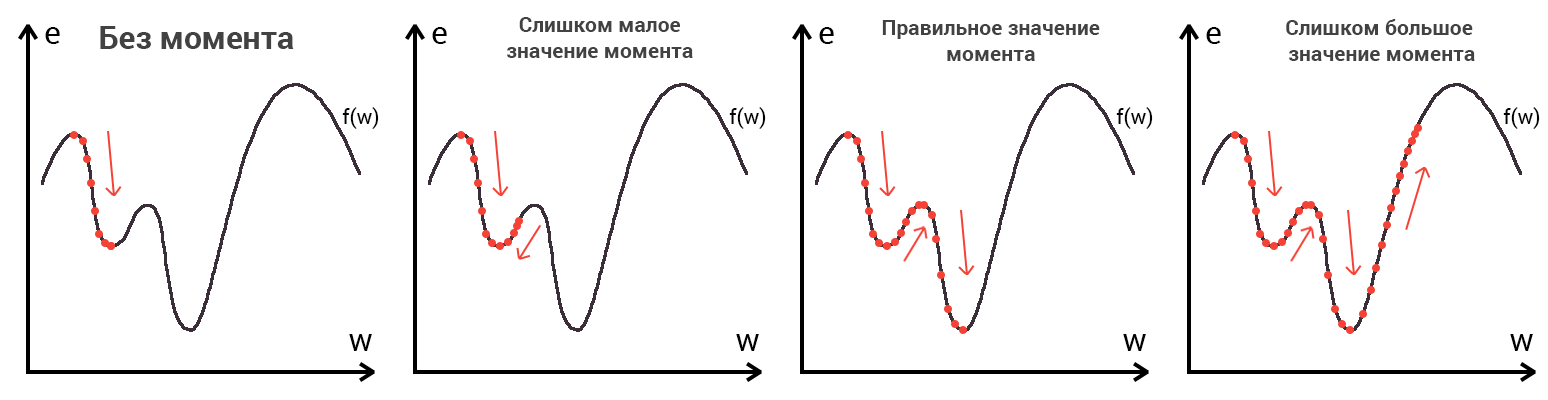
Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:
Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?
Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже).
Что такое Метод Обратного Распространения (МОР)?
Вот мы и дошли до того момента, когда мы можем обсудить, как же все таки сделать так, чтобы ваша НС могла правильно обучаться и давать верные решения. Очень хорошо МОР визуализирован на этой гифке:
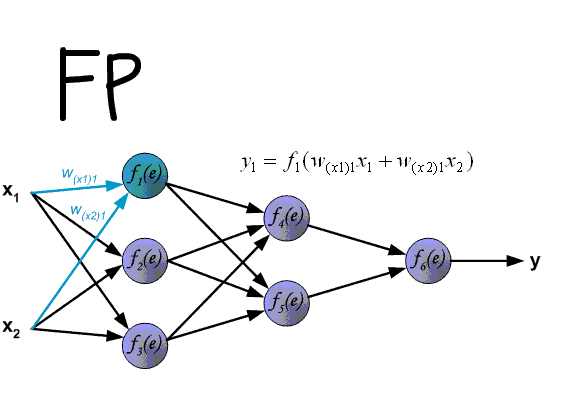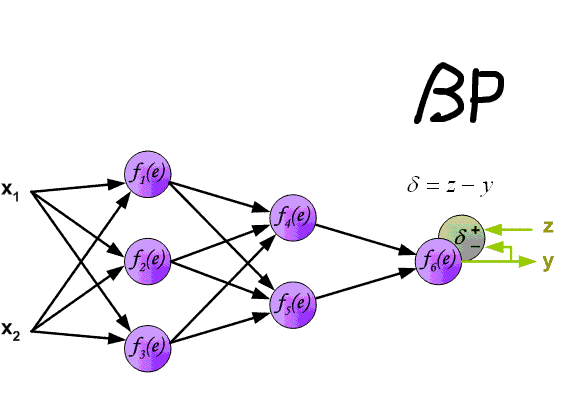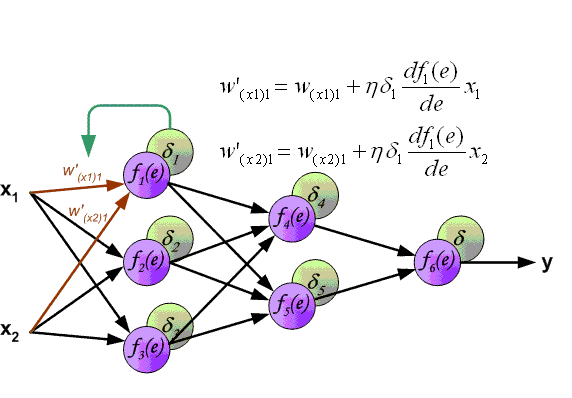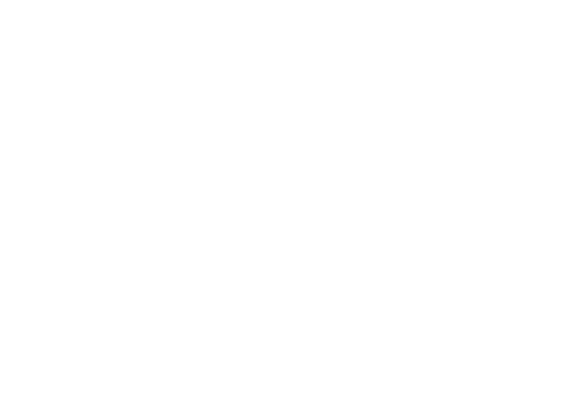
А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).
Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.
Данные задачи из предыдущей статьи
H1input = 1*0.45+0*-0.12=0.45
H1output = sigmoid(0.45)=0.61
H2input = 1*0.78+0*0.13=0.78
H2output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
Результат — 0.33, ошибка — 45%.
Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение δ (дельта) по формуле 1. 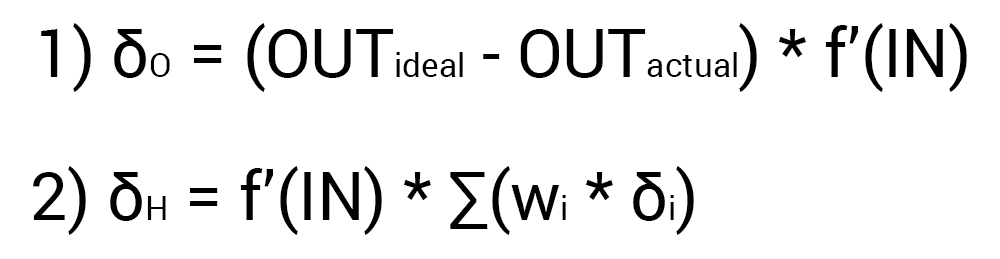
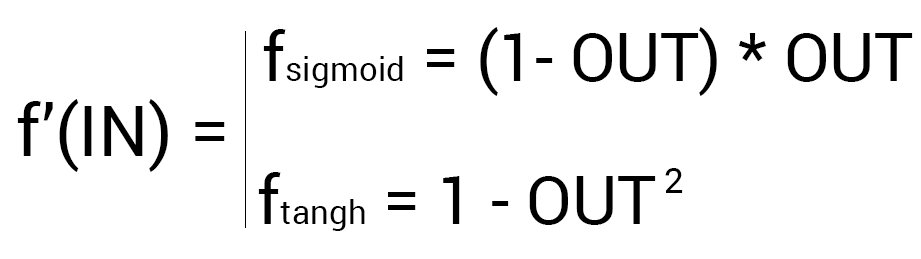
Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.
На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для H1:
Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так: 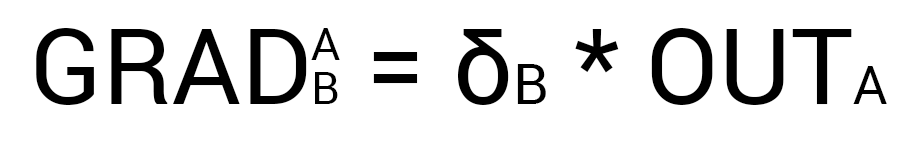
Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:
Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом: 
Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.
Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, α (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему Δw5.
Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для H2.
И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.
Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.
Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала.
Что еще нужно знать о процессе обучения?
Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).
Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.
Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.
Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.
Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.
Вкратце о каждом методе:
Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел Δw, сразу обнови соответствующий вес.
Пакетный метод же работает по другому. Мы суммируем Δw всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.
Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму Δw всех весов в той или иной группе.
Что такое гиперпараметры?
Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:
В других типах НС присутствуют дополнительные гиперпараметры, но о них мы говорить не будем. Подбор верных гиперпараметров очень важен и будет напрямую влиять на сходимость вашей НС. Понять стоит ли использовать нейроны смещения или нет достаточно просто. Количество скрытых слоев и нейронов в них можно вычислить перебором основываясь на одном простом правиле — чем больше нейронов, тем точнее результат и тем экспоненциально больше время, которое вы потратите на ее обучение. Однако стоит помнить, что не стоит делать НС с 1000 нейронов для решения простых задач. А вот с выбором момента и скорости обучения все чуточку сложнее. Эти гиперпараметры будут варьироваться, в зависимости от поставленной задачи и архитектуры НС. Например, для решения XOR скорость обучения может быть в пределах 0.3 — 0.7, но в НС которая анализирует и предсказывает цену акций, скорость обучения выше 0.00001 приводит к плохой сходимости НС. Не стоит сейчас заострять свое внимание на гиперпараметрах и пытаться досконально понять, как же их выбирать. Это придет с опытом, а пока что советую просто экспериментировать и искать примеры решения той или иной задачи в сети.
Что такое сходимость?
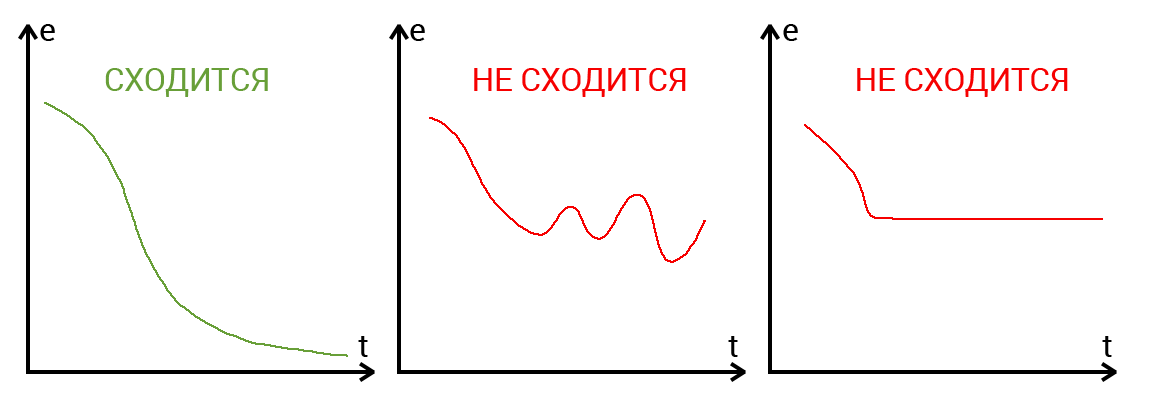
Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС.
Что такое переобучение?
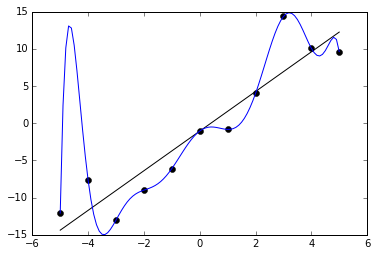
Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом.
Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться.