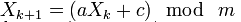для чего нужен рандомайзер
Хитрости как выбрать победителя в Инстаграме в комментариях
Конкурсы и различные розыгрыши – отличный способ взаимодействия с аудиторией. Однако, подвести итоги иногда бывает очень тяжело. Разберемся, какие методы и сервисы для этого существуют.
Выбрать победителя в Инстаграме в комментариях
Если вы хотите провести максимально честный розыгрыш среди своей аудитории, то предлагаем вам несколько вариантов это сделать:
Эти методы идеально подойдут для начинающих блогеров, весь процесс не будет занимать сильно много времени. Но если вам нужен вариант еще проще, то стоит рассмотреть специальные сервисы для поиска победителей по комментариям.
Программы для розыгрыша в Инстаграм
В плане использования сайт довольно простой и интерфейс не вызовет у вас непонимания. Если хотите все провести качественно и быстро – можете попробовать.
Рандомно выбрать победителя
Очень часто при проведении конкурса, особенно где участвует много людей – возникают недопонимания и обвинения в не правдивости результатов. Чтобы этого избежать, аудитория должна знать, как вы выбираете победителя. Это, естественно, должно быть рандомно.
Чтобы обеспечить случайность победы пользователя, советуем взять на вооружение следующие советы:
Конечно, первые конкурсы могут быть неудачными. Провести все идеально и без помех порой не получается даже у крупных блогеров. Если произошли какие-то форс-мажорные ситуации или вы затянули с розыгрышем, то сообщите об этом своей аудитории. Лучше всего будет посмотреть, как конкурсы проводят более авторитетные пользователи. Это хороший способ быстро научиться делать все качественно.
Выбрать победителя по лайкам
Это не менее популярный способ проведения таких мероприятий. Зачастую, такой вариант даже будет проще в плане реализации. Кстати, хороший совет: укажите в условиях, что нужно не только лайкнуть публикацию, но и написать комментарий. Так вы сможете разыграть приз среди заинтересованных пользователей.
Как видите, подвести итоги можно абсолютно прозрачно и честно, если такая цель стоит перед вами. Подумайте, какой способ подойдет именно вам лучше всего.
Сергей и компания
SMM специалисты с опытом работы в соцсетях. На протяжении долгого времени занимаемся продвижением профилей в социальной сети Instagram и VK. Можем ответить на интересующие вас вопросы.
Подробно о генераторах случайных и псевдослучайных чисел
Введение
Как отличить случайную последовательность чисел от неслучайной?
Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Уязвимости ГПСЧ
Линейный конгруэнтный ГПСЧ (LCPRNG)
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений
Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Предсказание результатов линейно-конгруэнтного метода
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Взлом встроенного генератора случайных чисел в Java
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
Вывод данной программы будет примерно таким:
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Взлом ГПСЧ Mersenne twister в PHP
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Область для взлома
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Задание распределения для генератора псевдослучайных чисел
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Треугольное распределение
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
Экспоненциальное распределение
Тесты ГПСЧ
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.
Случайные числа не случайны
FullStack CTO
FullStack CTO
Как создать генератор случайных чисел на JS и предсказать Math.random()
Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании — напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать.
Генератор псевдослучайных чисел и генератор случайных чисел
Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.
Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.
Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.
Энтропия — это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()
ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ — это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.
Придумываем алгоритм ГПСЧ
Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).
Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:
Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.
А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:
Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9. Кстати, так выглядит распределение по выпадению чисел при 10000 итерациях:
Распределение очень неравномерное, но мы получим генератор чисел от 0 до 9.
Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:
Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random() — это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.
Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них — это Линейный конгруэнтный ГПСЧ(LCPRNG).
Линейный конгруэнтный ГПСЧ
Линейный конгруэнтный ГПСЧ(LCPRNG) — это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
где a(multiplier), c(addend), m(mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа — т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:
Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).
Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ — это проблема. Если говорить про другие задачи, то эти свойства — могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.
Еще одно свойство — воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.
Как устроен Math.random()
Как устроен алгоритм Math.random() — интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:
Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.
Исправил ошибку в алгоритме MWC1616 (пропущенные скобки). Эта же ошибка повторяется и в статье https://v8project.blogspot.ru/2015/12/theres-mathrandom-and-then-theres.html
то видим, что должны быть скобки:
Предсказываем Math.random()
Чем это было чревато? Есть такой квест: https://alf.nu/ReturnTrue
Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:
Этот код работал в 70% случаев для Chrome
Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие — числа можно предсказать.
Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.
Новый алгоритм выглядит так:
Сrypto Random Values
Пример генерации случайного числа:
Но, в отличие от ГПСЧ Math.random(), этот метод очень ресурсоемкий. Дело в том, что данный генератор использует системные вызовы в ОС, чтобы получить доступ к источникам энтропии (мак адрес, цпу, температуре, etc…).
Материалы про Math.random()
Больше про random в спецификации:
Хорошая статья про работу рандомайзера
Пример реализации предсказателя с Math.random()
Кстати, следить за обновлениями и прочими материалами от меня можно в телеграм канале: @prowebit
Концепт «правильного» определения случайного победителя
Знаете, иногда я вижу, что группе людей нужно выбрать некий случайный объект. Например, дежурного, если нет графика, или он запутался (по поводу «правильных» графиков дежурств я бы тоже рассказал). Или же, что меня начало в последнее время раздражать, победителя в каком-либо конкурсе репостов.
Проблема следующая. Организаторы конкурса заявляют, что вот вам последовательность действий, совершите её для участия в конкурсе (например, сделайте репост этой записи), а затем мы такого-то числа выберем случайного победителя из репостнувших. Люди совершают все эти действия, приходит долгожданный день и мы получаем…
Победителя. В лучшем случае мы так же получим видео, как организатор при помощи random.org выбирает номер, а затем находит победителя в какой-нибудь таблице.
Однако здесь кроется одна неувязка. Организаторы обещают честный рандом, но ничего, кроме их честного слова мы не имеем. Они могут сотни раз снимать видео, пока не выпадет нужное число, подменить сайт на локалхосте и так далее. Нет никаких гарантий, что мы получили действительно случайный выбор.
Я же считаю, что системы должны быть спроектированы таким образом, чтобы совершить нечто неправильное в них не было возможно, поэтому…
Итак, мы имеем группу из N участников. Нам требуется получить нечто случайное, чтобы каждый участник был согласен с тем, что этот случайный объект был получен честным образом.
В реальном мире, если выбор бинарен — мы можем попросить кого-нибудь подбросить монетку (впрочем, можно бросать её долго, получить нужное кол-во бит и затем получить что угодно). И мы будем видеть, что он действительно её бросил, что она взлетела, крутилась в воздухе, приземлилась и выпал действительно орёл или решка.
Но в интернете мы не можем видеть, что кто-то действительно что-то куда-то подбрасывает.
Поэтому нам нужен алгоритм, который бы не был централизированным и был бы легко проверяем. Первое, что приходит на ум — попросить у каждого участника любых случайных данных, склеить их с данными полученными от других участников, посчитать от этого какой-нибудь хеш и использовать его как зерно для генератора псевдослучайных чисел.
Но в такой схеме есть два недостатка — время и посредник.
В реальном мире мы могли бы написать случайные данные каждого участника на бумажки, кинуть их в урну, а затем, когда все бросили свои данные — достать их из урны и провести ритуал получения Истинного Рандома. В наших реалиях, к сожалению, у нас нет такой урны.
Мы можем попробовать обменяться своими данными с другими участниками, однако в игру вступает время. Нельзя обменяться данными одновременно. И тогда участник, который должен «бросить» свои данные последним, имея данные всех остальных может подобрать такие данные, которые бы заставили бы рандом стать на его сторону.
Или же можно попросить кого-нибудь «подержать» данные для нас, т.е. найти незаинтересованного посредника. Однако этот вариант не является сильно надёжным, т.к. посредника всё же можно чем-либо заинтересовать.
Второе, что приходит на ум — нужно каким-то образом зашифровать нашу виртуальную урну, чтобы посмотреть её содержимое можно было только после окончания вбрасывания своих листков.
Можно действительно зашифровать, например, так: каждый участник создаёт свою пару публичного и приватного ключа, делится со всеми своим открытым, шифрует свои данные, делится со всеми зашифрованными. Когда раунд обмена зашифрованными данными закончился — все открывают свои закрытые ключи, расшифровывают зашифрованные данные, получают незашифрованные, склеивают, хешируют, кормят ГПСЧ, получают вожделенный рандом.
Но согласитесь, что для выбора одного случайного числа создавать криптоключи — довольно дорого. Поэтому вместо этого можно воспользоваться теми же хешами. В начале все договариваются о некой соли, чтобы никто не мог использовать какой-либо словарь коллизий и открывать совершенно другие данные. Затем хешируют свои данные (должно быть достаточное количество бит, чтобы невозможно было за разумное время просто отбрутфорсить хеши всех участников), делятся, вскрываются.
Т.е. мы получаем децентрализированную трёхраундную (обмен ключами/выбор соли, «закрытое голосование», «вскрываемся») систему выбора некого случайного зерна группой людей. Причём каждый из людей может собственноручно проверить легитимность итогового выбора. И ни участники, ни организатор не могут повлиять на конечный исход.
Применимо ли это на практике в виде чего-либо? Можно ли улучшить схему?
Рандомайзер Вконтакте
Опытные админы знают, что такое рандомайзер Вконтакте и часто прибегали к его использованию. Кто не знаком еще с райндомайзером или хочет узнать, что это такое, Вам будет интересна для ознакомления на будущее данная статья.
Понятие рандомайзера не относится конкретно к Вконтакте или социальным сетям, скорее это англицизм генератора случайных чисел. Рандомайзер можно определить, как программу или программный алгоритм, которая призвана выбрать определенный объект из массива подобных объектов на основе случайного фактора.
В сети существует множество скриптов, с помощью которых на своем сайте при совершении определенного действия (например, клике, скролинга до метки, просмотре видео и так далее) получить случайным образом любое число.
Также для примера, можно привести несколько ресурсов, которые посвящены рандомайзерам для всевозможных случаев жизни:
Для чего пригодится рандомайзер Вконтакте
Казалось бы, ну вы падают случайные числа при определенном действии, но для чего может пригодиться райдономайзер Вконтакте? Для владельцев или администраторов групп и сообществ, в которых периодически проводятся опросы среди подписчиков, призовые конкурсы, розыгрыши подарков, без рандомайзера просто не обойтись.
Конечно, условия конкурса бывают разные, например, можно выбрать победителя по истечению времени того, кто больше всех написал полезных комментариев, опубликовал больше всех за это время авторских фото или же того, кто последний успел совершить какое-то действие.
Рандомайзер Вконтакте – инструкция
Для рандомайзера Вконтакте инструкции однозначной не существует, так как у каждого свои способы его использования, а методы определения призеров в конкурсах могут быть разными. Но следует понять принцип, на котором основано использование рандомайзеров для определения победителя того или иного конкурса.
Если победителем конкурса может стать любой участник, который выполнил минимальные условия, например, сделал репост требуемого поста своим подписчикам, тогда необходимо сформировать список всех участников. В таком случае можно выделить 3 способа определения победителей Вконтакте.
Последний вариант кажется большинству участников наиболее прозрачным, вызывающим больше всего доверия с вынесением не предвзятых решений. Админ или организатор конкурса в таких случаях не может повлиять на выбор, который совершит третья сторона.
Для читателей можно привести список одних из самых используемых программ и сервисов, которые будут Вам очень полезны при проведении конкурсов.
• vk.com/app4921233
• vk.com/app3407122_213333592
• vk.com/app3287003_162298533
• vk.com/talk_to_friends
• vk.com/app3872419_162298533
• kamaninga.com
• megarand.ru
• mrandom.com
Большинство сторонних сервисов хорошо интегрируются с Вконтакте. Например, с помощью сервиса kamaninga выбрать победителя очень просто.
Сложного ничего нет в этом. Проводите интересные и справедливые конкурсы и радуйте своих подписчиков. Также помните, что правильно оформленная группа с интересными документами и материалами, а плюс к этому с периодическими конкурсами и подарками будет успешно расширятся.